在隧道抗震分析的多种数值计算方法中,到目前为止,还没有令人满意的完善的数值方法。现有的数值模拟方法,大体上可以分为两种:第一种是弹性计算模型,可以将静力与动力计算分开,然后将所得结果进行叠加(瓦尔夫,1989),得到的是隧道在遭遇地震时,重力与动力波对隧道的影响结果; 另一种是考虑材料的弹塑性计算模型,此时已经是非线性阶段,叠加原理不成立,因此不能分开计算,可以考虑把重力当作荷载并入动力计算,以模拟非线性反应。

对于岩土结构的地震响应数值模拟,首先采用弹性计算模型是必要的,可以初步获得结构的的弹性地震峰值反应,为结构物的强度设计提供直接依据; 另一方面,由于岩土的本构关系实质上是一种塑性和弹塑性关系,因此,要想获得结构物的更准确的地震动力反应,仅仅依靠弹性分析是远远不够的,必须进行弹塑性时程分析。本文采用的方法是首先进行弹性分析,然后进行塑性分析,并对两种分析方法的结果进行对比,以期获得一些有意义的结论。

隧道不同于地上结构,隧道周围有围岩的约束作用,隧道与围岩是共同作用、协调变形。对于有限元计算模型来说,不可能将其取为无限大,只能切取其中一部分来计算,与其它部分的关系通过设置边界即人工边界来处理。这个边界实际上是不存在的,只是为了模型分析而人为设置的,因此,要求边界条件能够有效地消除边界的波反射问题,而且要在人工截断边界处满足应力与位移与未截断时的无限域相同(廖振鹏,2002)。

Lysmer等(1972)基于一维平面波动理论提出来的粘性动力人工边界目前是较为成熟的,该边界在人工选取的计算模型截断边界上,加上粘壶,以模拟无限地基的作用。底部采用粘性边界,能够模拟地震能量传至基础底面时,一部分被反射后向下方的能量逸散。侧面采用粘性边界能够模拟地震能量向两侧方向无限远处的传播。

Lysmer等(1972)提出的粘性边界通过在边界引入粘性反力来吸收波动的反射能量,认为在边界面上应给予的粘性正应力σ和剪应力τ分别为

σ=aρv_Pw'; (1)

ττ=bρv_Su'.(2)

式中,w'和u'分别为介质运动的垂直速度和切向速度; a和b为待定系数,其值可由波的反射、折射理论确定; ρ为介质密度; v_P和v_S分别为纵波(P波)和横波(S波)的传播速度(Lysmer等,1972)。

本文以P波为例说明粘性边界的原理及其适应条件(S波与其类似)。设入射P波与介质表面的夹角为θ,则反射P波与介质表面的夹角也是θ,再设反射S波与介质表面的夹角为β,则可得到振幅为1的入射P波的能量为

E=1/(2S)ρv_Sω²sinθ.(3)

式中S为P波与S波的波速比,ω为波动的圆频率。反射波动能量为

E'=1/(2S)A²ρv_Sω²sinθ+1/(2S)ρB²v_Sω²sinβ.(4)

式中A、B分别为反射P波和反射S波的振幅,由此可以得到能量比为

η=E/(E')=A²+SB²(sinβ)/(sinθ).(5)

要消除边界上的波的反射,需要能量比η等于零。在待定系数a=b=1的情况下,η的大小主要受入射角θ和泊松比μ的影响。一般岩土介质的μ值在0.2和0.3之间,此处假设μ=0.25,则θ=15°时,η为0.1左右,θ=30°时,η即小于0.05,若θ大于45°,则η接近于零(国胜兵,2002)。

本文采用的波动为垂直入射,入射角为90°,岩土介质以及衬砌泊松比大都在0.2～0.3,完全满足粘性边界的条件,而且粘性边界概念清晰、理论成熟,结果可靠,尤其适用于岩土—结构的动力相互作用分析,故本文采用粘性人工边界。

地震波的传播方向是不确定的,通常可以把地震波在岩体中的传播分解为3个分向,而且3个分向所传播的能量是存在很大差异的。从现有地震资料来看,在水平方向传播的地震波往往具有较大的振幅,并传播了地震大部分能量,而且,对于隧道等地下结构来说,水平横向地震反应也是对结构物最不利的。因此,本文主要研究水平方向上传播的地震波对隧道造成的地震动力作用,粘性边界只施加水平方向动力激励。

FLAC3D动力计算中,可采用两种阻尼形式:瑞利阻尼和局部阻尼。由于瑞利阻尼与频率以及临界阻尼比有关,而且在计算时增加计算时间,因此本次计算采用局部阻尼。

局部阻尼主要通过在振荡循环过程中单元节点或结构节点质量的添加和删减来产生作用。由于添加的质量等于删减的质量,因此存在一个总体的质量守恒。阻尼系数也称为局部阻尼,局部阻尼有以下几个特点:

(1)只有加速运动才会被减弱,匀速运动不引起误差阻尼力。

(2)阻尼系数为常数,没有维数。

(3)阻尼与频率无关,不同频率的区域可采用相同的阻尼系数。

FLAC3D中的阻尼方程类似于滞后阻尼,每次循环中的能量损耗不受该循环步应变率的影响,而且不必确定频率。

(1)总体分析

① 通过表2与图5可以看出,峰值位移均发生在明暗洞交接处,且在仰拱位置出现X方向位移最大值,出现时刻为3.54 s;

② 内力峰值均出现在埋深最大的位置,墙脚位置是出现弯矩和剪力最大的位置,而最大轴力位置出现在拱腰。

表2 弹性分析峰值位移内力表

图5 峰值位移断面仰拱位移时程曲线

由于左右两线所得结果从趋势上来讲基本相同,因此以右线为例加以说明。

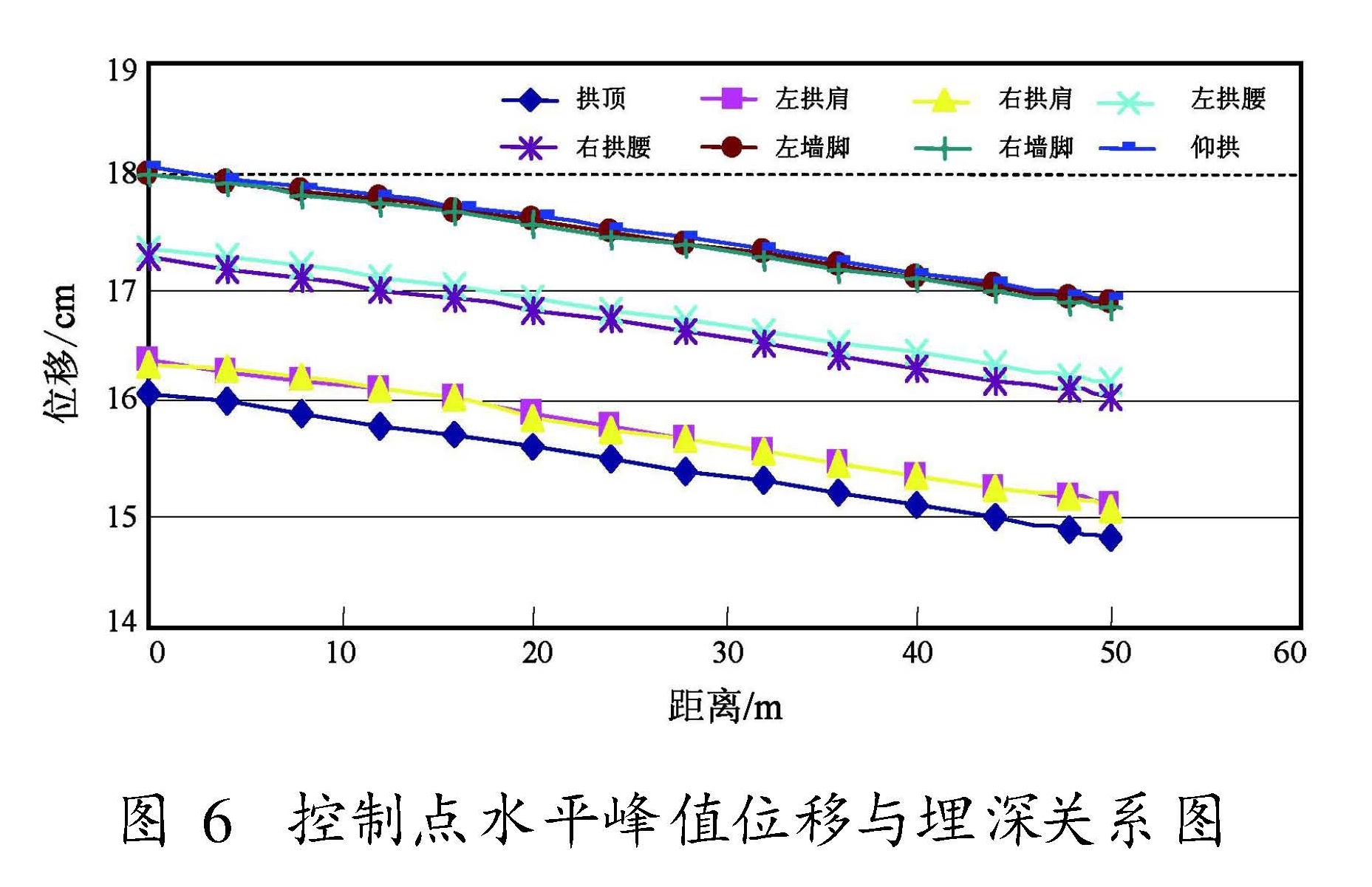
从图6可以看出,隧道水平向位移峰值随着埋深的增大有减小的趋势,即埋深越大位移峰值越小。但是增加的幅度不是很明显,左线控制点5、6、7和右线控制点2、3、4相比,相同位置的控制点的内力峰值要大,这说明了双线隧道在地震

图6 控制点水平峰值位移与埋深关系图

(3)内力结果分析

图7是内力峰值随纵向距离的变化曲线。由图可以看出,随着埋深的增大,内力的峰值有增加的趋势,但是增加的幅度不是很明显。左线控制点5、6、7和右线控制点2、3、4比,相同位置的控制点的内力峰值要大,这说明双线隧道在地震来临的时候,相互间有一定的影响,表现在右线左侧拱腰、拱脚、墙脚的位移和内力要大于右线右侧拱腰、拱脚、墙脚的位移和内力。左线右侧控制点的位移和内力亦大于左线左侧控制点的位移和内力。

图7 隧道右线控制点峰值弯矩(a)、轴力(b)、剪力(c)沿纵向变化曲线

计算结果如图8、表3所示。

图8 塑性区分布图

表3 弹塑性分析峰值位移内力表

从图8可以看出,地震波作用停止时,隧道围岩出现大面积塑性区。

弹塑性计算所得位移峰值与内力峰值随埋深增大的变化规律与弹性计算时基本相同,但是峰值大小却差异很大。

从表3可以看出,围岩屈服后,水平方向的峰值位移明显增大,内力峰值也有增大趋势,这是地下结构不同于地上结构之处,充分证明了围岩与隧道结构共同作用的重要性。位移峰值与内力峰值随埋深增大的趋势与弹性计算时基本相同。埋深越大,内力越大,这也就证明了重力在数值模拟中的重要性,这与一些文献上所说的重力在动力计算中可以忽略的说法有些不符。

近年来,国内不少学者利用岩土—结构相互作用来研究地下结构的抗震问题,得出不少有意义的结论。本文运用FLAC3D软件,从岩土—结构相互作用出发,研究了双线浅埋隧道在地震荷载下的反应,认为衬砌最大峰值位移随着埋深的增大而逐渐减小,而内力在总体上则随着埋深的增加而增加,但并不是单调递增,最大峰值内力数值分别为:弯矩-76.15 kN·m,轴力2 227 kN; 剪力443 kN,与静力作用下的内力相比,弯矩和剪力的增加幅度比较大。也就是说,地震荷载作用下,主要产生的是弯矩和剪力,这与国胜兵等(2002)、匡志平等(2002)、毕继红等(2003)、高峰等(2006)的研究结果一致。

另外,本文研究发现,地震荷载作用下,轴力幅度的增加值与弯矩、剪力的增加值相比,增加稍小,但是,与重力产生的效应相叠加后,亦产生相当大的轴力,这对衬砌混凝土的受压承载力会造成一定的影响,因此隧道洞口段的轴向力是不容忽视的。这也说明了地震发生时隧道洞口是抗震薄弱环节,需采取一定的加固补强措施。