基金项目:广州航海高等专科学校自然科研基金(200612B12)资助.
(Department of Civil Engineering,Guangzhou Maritime College,Guangzhou 510700,Guangdong,China)
soil-structure interaction; base isolation; slab-column structure; seismic response
备注
基金项目:广州航海高等专科学校自然科研基金(200612B12)资助.
对广州地区一例地基—基础—隔震板柱结构动力相互作用体系进行了计算分析。通过与常规设计方法及非隔震体系的比较,研究了该体系地震反应的变化规律,并分析了阻尼比、地基土特性、基础刚度、基础型式、基础埋深、土体深度、上部结构刚度和地震波等因素对相互作用体系动力特性及地震反应的影响。
Exemplified by an engineering building of Guangzhou,China,the seismic response of slab-column structure-raft foundation-soil interaction system was analysed using 3-D finite element method.Through comparing the interaction results with non-interaction results of the system,the varying rules of dynamic response was studied,and the influences of some factors on the systems dynamic characteristic and seismic responses,such as the damping ratio,soil property,the rigidity and type of foundation,the buried depth of foundation,the rigidity of structure and the seismic wave were discussed.
引言
自1906年美国学者Turner首次采用钢筋混凝土平板—柱结构以来,由于其结构形式简单、传力路径简捷、建筑效果良好等多重优势,而被广泛应用于各类工程建设中,但该结构体系抗侧刚度较差,若设计施工不当,地震作用下可能会造成较严重的破坏。我国《建筑抗震设计规范》(GB50011—2001)对板柱结构体系的应用作了较严格的规定,致使设计人员对在抗震设防区使用这种结构体系有疑虑,一定程度上限制了板柱结构的应用,而在实际工程中对这种结构有大量的需求,事实上,在美国及其它一些国家,板柱结构是最常被采用的结构形式之一,研究如何有效抵抗地震作用,提高板柱结构的抗震性能很有必要。
为了有效抵抗地震作用,工程结构抗震设计方法已逐渐由传统的加强结构强度向减轻地震作用和改善结构延性方向转变。其中,基础隔震作为一种有效的被动控制方法被用于建筑结构、桥梁等工程领域。为改善板柱结构的抗震性能,笔者将隔震技术应用于该结构体系(张卫东,2006; 2007),按现行抗震规范刚性地基假定的三维非线性时程分析表明,隔震是提高板柱结构抗震性能的有效途径。但结构—基础—地基作为整体,在静、动力作用下三者相互制约、相互作用的事实是客观存在的(董建国等,1997; 窦立军等,1999; 孙树民,2001)。笔者所做的三维整体静、动力相互作用分析表明,考虑相互作用对板柱结构的合理设计很有必要(张卫东,2007)。笔者在此基础上,探讨了土—结构相互作用对设置基础隔震层的板柱结构的影响,通过将其与常规设计方法及非隔震体系进行比较,研究了隔震板柱体系地震反应的变化规律,并对阻尼比、地基土特性、基础刚度、基础型式、基础埋深、上部结构刚度、地震波等因素对隔震体系地震反应的影响进行了分析。
1 工程概况
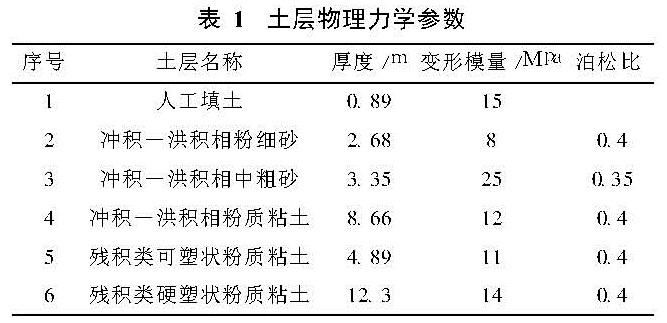
某建筑为现浇板柱结构,地上9层,层高3 m,地下1层,层高3.8 m,纵、横向柱距均为6 m,5×3跨。现浇楼板厚200 mm,柱截面尺寸为(500×500)mm2; 房屋周边设边梁,截面尺寸为(300×500)mm2; 剪力墙厚200 mm,双向布置在核心(形成筒)。采用筏板基础,筏板厚1.2 m,基底埋深5 m,地下室侧墙厚350 mm,上部结构及基础均采用C30混凝土。土体采用广州江夏附近的实际土层分布,其物理力学参数如表1所示,质量密度统一取1 800 kg/m3。
该建筑在基础顶部设置隔震层,选用铅芯橡胶隔震支座,竖向刚度为2 400 kN/mm。水平应变为50%时的水平刚度为2.56 kN/mm,阻尼比为0.31; 水平应变为250%时的水平刚度为1.26 kN/mm,阻尼比为0.19。
2 建立三维分析模型
2.1 单元选择利用ANSYS软件参数化设计语言建立三维模型。由于本文主要分析考虑隔震板柱结构—基础—地基相互作用的结构地震反应相对于常规设计的变化规律,故对钢筋的处理是与混凝土一起采用整体式模型。柱和边梁采用空间杆单元,楼板、剪力墙和筏板采用壳单元,地基土采用三维实体单元模拟。隔震层采用弹簧阻尼单元,用双线性模型模拟其在地震作用下的非线性恢复力特性。
2.2 边界处理及计算区域为模拟地震能量向场地远方的逸散,目前的方法有设置人工粘性边界、粘—弹性边界、透射边界、旁轴边界、自由边界等,以提高计算精度。其中由Deeks等(1994)推导得出的粘—弹性人工边界有良好的应用效果,熊辉等(2004)将该种人工边界与固定边界进行对比分析,结果为顶点加速度及位移仅有1.3%和4.1%的差别。为简化计算,便于将土—结构相互作用由研究领域推广到工程应用中,本文对土体采用简单截断边界,底部固定,4个侧面除竖向外另两个方向位移自由度约束。土体范围沿建筑物两个方向各取其结构尺寸的3倍,土深取18 m。
3 分析工况
为了进行对比分析,建立了基础固定板柱结构(S)、基础隔震板柱结构(SG)、考虑土—结构相互作用的板柱体系(SSI)、考虑土—结构相互作用的基础隔震板柱体系(SGI)4种模型进行计算分析。在此基础上,为研究土—结构相互作用对隔震板柱体系地震反应的各种影响因素,另对不同土性、不同基础(刚度、型式)、不同基底埋深、不同土体深度、不同上部结构、不同阻尼比、不同地震波共22种工况进行了计算分析,其工况条件为:
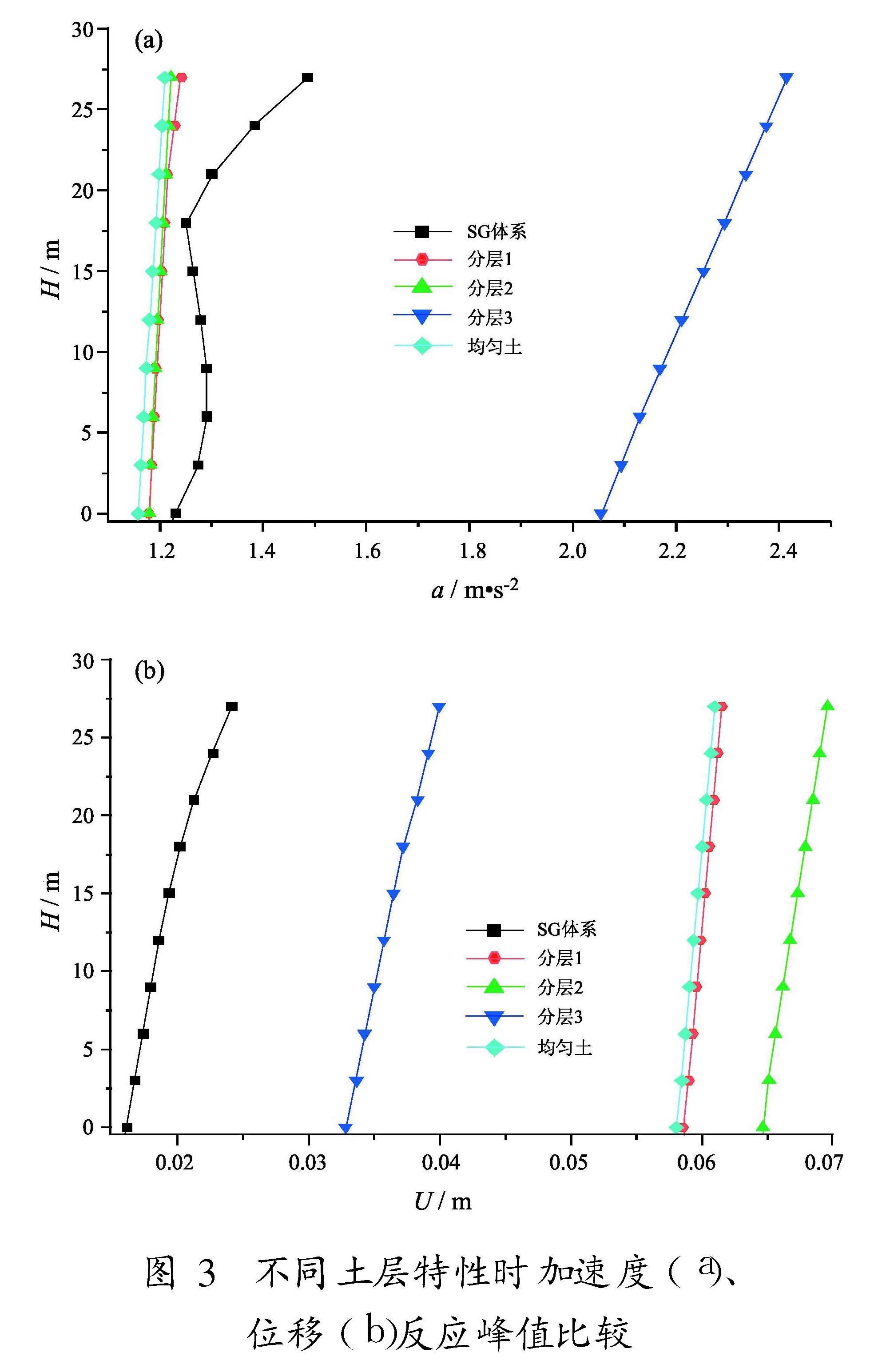
(1)不同土性:在基本模型取广州实际土层(分层1:E1=8 Mpa,υ1=0.4; E2=25 Mpa,υ2=0.35; E3=12 Mpa,υ3=0.4; E4=11Mpa,υ4=0.4)的基础上,考虑另外3种情况:分层2(较软,E2=10 Mpa,υ2=0.4,其余同分层1); 分层3(较硬,E3=E4=38 Mpa,υ3=υ4=0.3,其余同分层1); 均质土(E=13.3 Mpa,υ=0.39)。
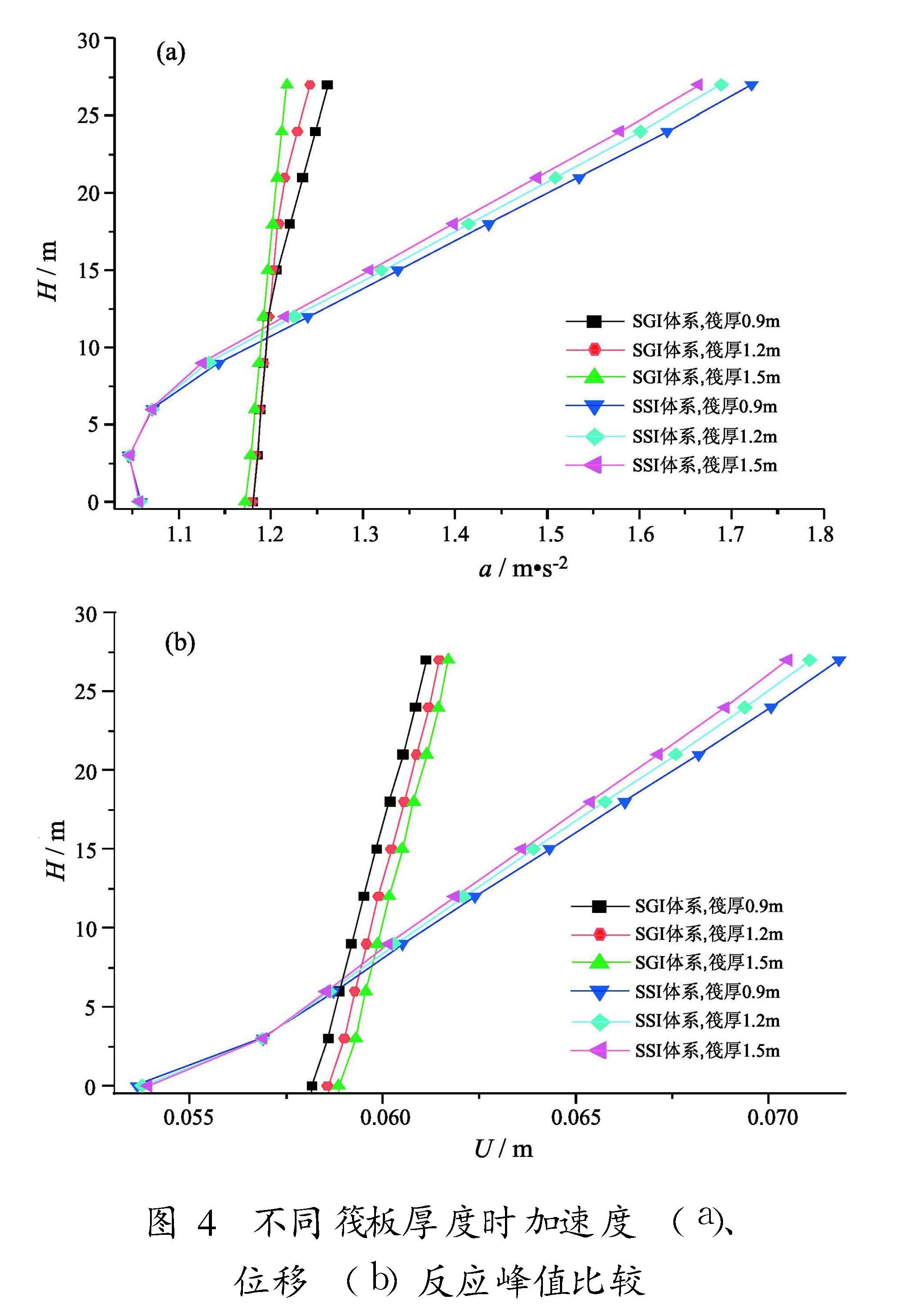
(2)不同筏板基础厚度:为研究基础刚度对SSI体系地震反应的影响,通过改变筏板厚度来改变其刚度,分别取为0.9 m、1.2 m、1.5 m。
(3)不同基底埋深:分别取为3 m、5 m、9 m。
(4)基础型式:保持上部结构不变,采用箱形基础进行计算,并与基本模型筏板基础进行比较。箱基顶板厚0.35 m、底板厚0.55 m、外墙厚0.4 m、内墙厚0.3 m。
(5)上部结构刚度:为研究上部结构刚度对SGI体系地震反应的影响,通过改变上部结构混凝土的强度等级、楼板厚度及柱截面尺寸来改变其刚度。即混凝土强度等级分别取C25、C30、C40; 楼板厚度分别取180 mm、200 mm、220 mm; 柱截面尺寸分别取(450×450)mm2、(500×500)mm2、(600×600)mm2。
(6)阻尼比:在土与结构相互作用问题中,地基的阻尼往往大于结构的阻尼,为了解阻尼比对共同作用体系地震反应的影响,对结构和地基输入不同阻尼比以及输入相同阻尼比的情况进行计算分析。阻尼比分别取:SGI、SSI体系0.05; SGI、SSI体系0.03; 上部结构0.05,地基土0.12; 上部结构0.05,地基土0.1; 上部结构0.03,地基土0.12; 上部结构0.03,地基土0.1;
(7)地震波:为研究不同地震波对SGI体系地震反应的影响,选取了3条地震波进行计算分析,即El-Centro波、Northridge波以及1条人工波,沿建筑物双向输入。
4 阻尼比的影响
不同阻尼比的SGI、SSI体系地震反应结果如表2。可见,采用不同阻尼比对SGI、SSI体系地震反应有不同程度的影响。总体而言,增大阻尼比可减小体系顶层加速度及位移,但减小程度不同。
(1)由于隔震层的作用,采用相同阻尼比时,SGI体系的顶层加速度及位移均低于SSI体系。
(2)本例SGI、SSI体系采用同一阻尼比时的地震反应均大于各自分别考虑结构和地基土阻尼比时的地震反应。但SSI体系的这种差异更大,二者相差1倍左右,而SGI体系的这种差异仅30%左右,表明由于隔震层的作用,地基土阻尼对SGI体系的影响已明显低于对SSI体系的影响。
(3)土阻尼比一定,单独改变上部结构阻尼比对SGI、SSI体系地震反应影响均很小。
(4)上部结构阻尼比一定,改变土阻尼比,SGI、SSI体系地震反应变化较明显(SGI体系变化没有SSI体系明显),但仍不如采用同一阻尼比时的变化显著。土阻尼比对SGI、SSI 体系地震反应的影响大于上部结构阻尼比的影响。由于隔震层的作用,这种影响对SGI体系明显降低。本例下面的分析采用上部结构阻尼比0.05,土阻尼比0.12。
5 动力特性分析
6 地震反应分析
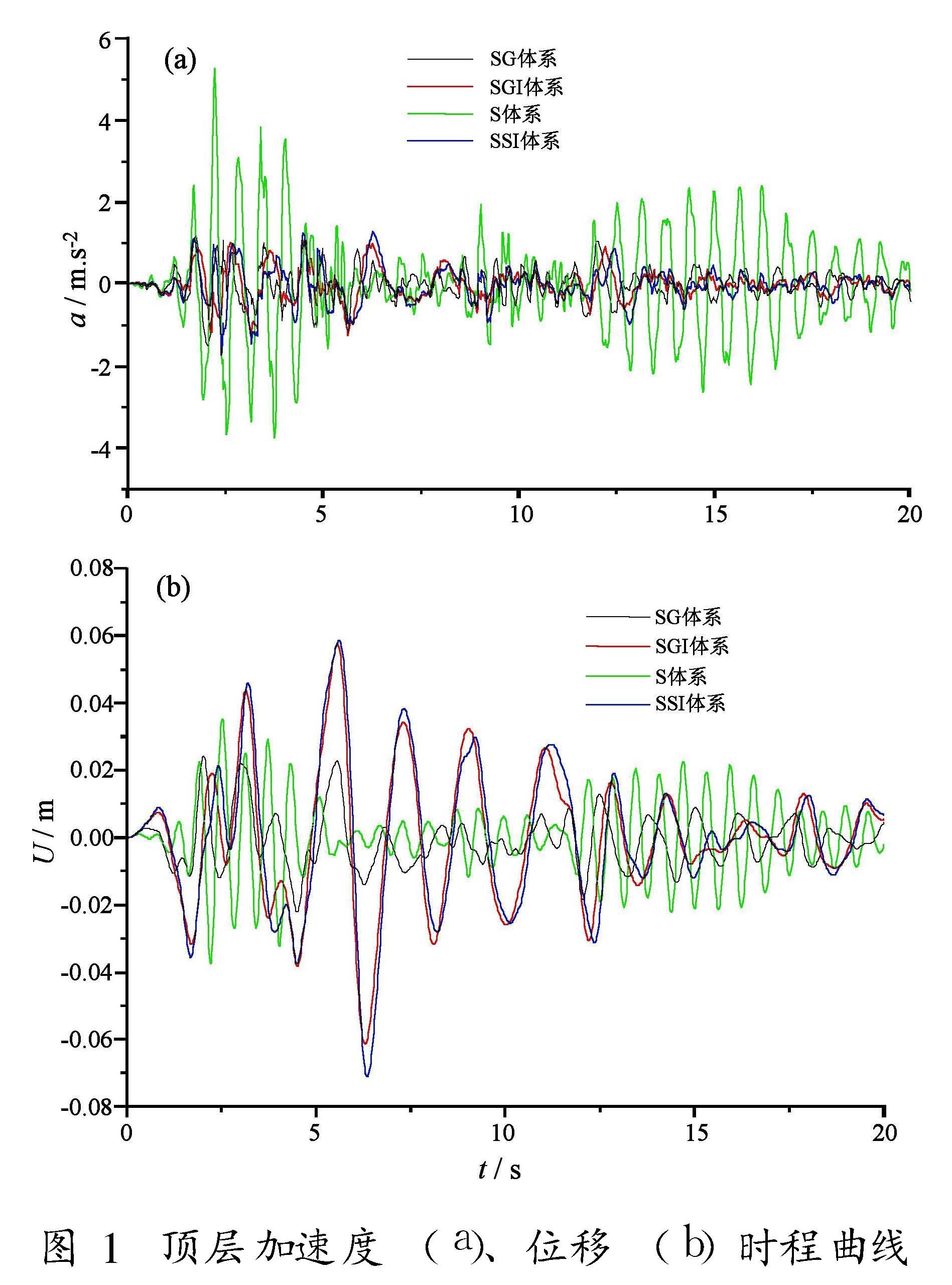
6.1 顶层加速度及位移时程反应分析图1为输入El-Centro地震波时顶层加速度及位移时程曲线。
由图1a可见,S体系的顶层加速度具有较大的峰值,且在整个时程一直处在较高水平。由于隔震层和地基土的作用,SG、SGI、SSI体系的加速度时程峰值降低很多,且三者较为接近; 由图1b可见,SSI体系的顶层位移峰值最大,比较4条位移时程反应的波形,S体系的顶点位移时程波形变化更频繁,SG、SGI、SSI体系的波形较平缓,表明地震波经过隔震层和地基土滤掉了其高频部分。6.2 加速度和水平位移沿楼层的变化图2为输入El-Centro地震波时加速度及位移反应峰值沿楼层的变化曲线。由图2a可见,S体系的加速度反应峰值最大,且层间相对加速度也最大。与S体系相比,SG体系的顶层加速度峰值减小了71.8%,SGI体系减小了76.5%,SSI体系减小了68%。隔震层起到了显著的隔震作用,上部结构以“整体平动”为主要振动形式,层间加速度几乎相同。由图2b可见,非隔震结构层间相对位移、结构中上部及顶点位移较大,而隔震结构的位移主要集中在隔震层,上部结构随隔震层“整体平动”,层间相对位移很小。比较SG与SGI、S与SSI可见,考虑土—结构相互作用后,结构侧移变形中除自身变形外,还包含了基础的平动和转动,因而SGI比SG的位移大,SSI比S的位移大(顶点位移峰值SGI为SG的2.65倍,SSI为S 的1.91倍),而层间相对位移均减小。
6.3 上部结构内力的变化本文为三维实体建模,因而可得到各构件的内力。输入El-Centro地震波时,比较S与SSI体系上部结构内力可知,考虑地基土的参与后,板柱结点处板剪力、柱轴力、地上2层以上柱弯矩及剪力均比常规设计减小,但地上1层一些部位的柱弯矩及剪力增加; 设置隔震层后,比较 SG与S体系结构内力可知,除角柱轴力增加5%左右外,其它内力均减小。比较SG与SGI体系结构内力可知,考虑土—结构相互作用后,边轴柱轴力均有所增加(20%左右),角柱剪力及弯矩增加10%左右,其它内力减小。
可见,相互作用对结构的影响是复杂的,尽管考虑基础位移(平动和转动)后,影响内力反应的最大加速度减小,但在结构某些部位的内力却是增大的,相关文献(鲍华等,2005; 邹立华等,2004)均未提及这一结果。这一点应引起设计人员的注意。
7 地震反应影响因素分析
7.1 土层特性的影响不同土层特性时SGI体系加速度及位移反应峰值沿楼层的变化如图3。由图3a可见,土层相对较软时(分层1、分层2、均质土),加速度反应峰值相差不大,均比SG时加速度反应减小,而土层较硬时(分层3),加速度反应峰值比SG时增大,可见,土层特性不同对SGI体系地震反应影响也不同。由图3b可见,考虑土—结构相互作用的位移反应峰值均比SG时增大。土层越软,位移反应峰值越大(分层2比分层1顶点位移峰值增大13.2%,分层3比分层1减小35.1%)。由分层1换算的均质土的SGI结构加速度及位移反应峰值与分层1几乎相同,这与非隔震结构体系的S与SSI 间的规律明显不同,可能是由于隔震层的作用明显减弱了土的分层对上部结构地震反应的影响。
7.2 筏板基础厚度的影响图4为不同筏板厚度时加速度及位移反应峰值沿楼层的变化。作为对比,图中同时给出了非隔震结构SSI体系的加速度及位移反应峰值变化曲线。可以看到,增加筏板厚度,SGI 体系的加速度反应峰值有所减小,而位移反应峰值有所增加,这与SSI体系的加速度及位移反应峰值均减小有所不同,但改变均不大(筏厚由0.9 m增加到1.5 m时,顶点加速度及位移峰值变化均未超过5%)。
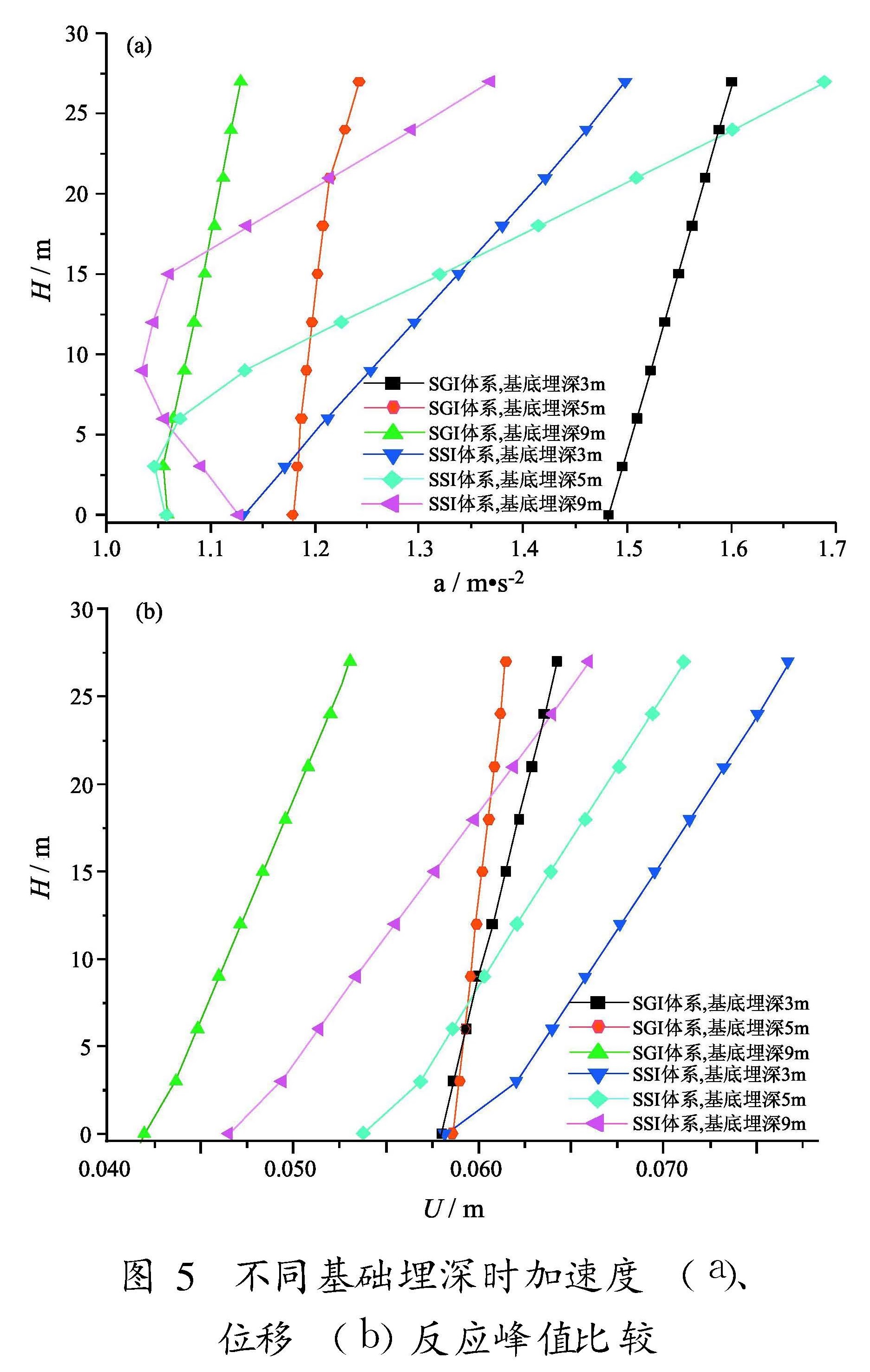
7.3 基础埋深的影响在基本模型的基础上,改变基底埋深,进行对比分析。图5为不同基础埋深时加速度及位移反应峰值沿楼层的变化。可见:基础埋深对SGI体系地震反应影响较大,变化规律不同于SSI体系。随基础埋深增加,SGI体系加速度及位移反应峰值均减小,且由于隔震层的作用,层间相对加速度及位移峰值均比非隔震SSI体系明显减小。
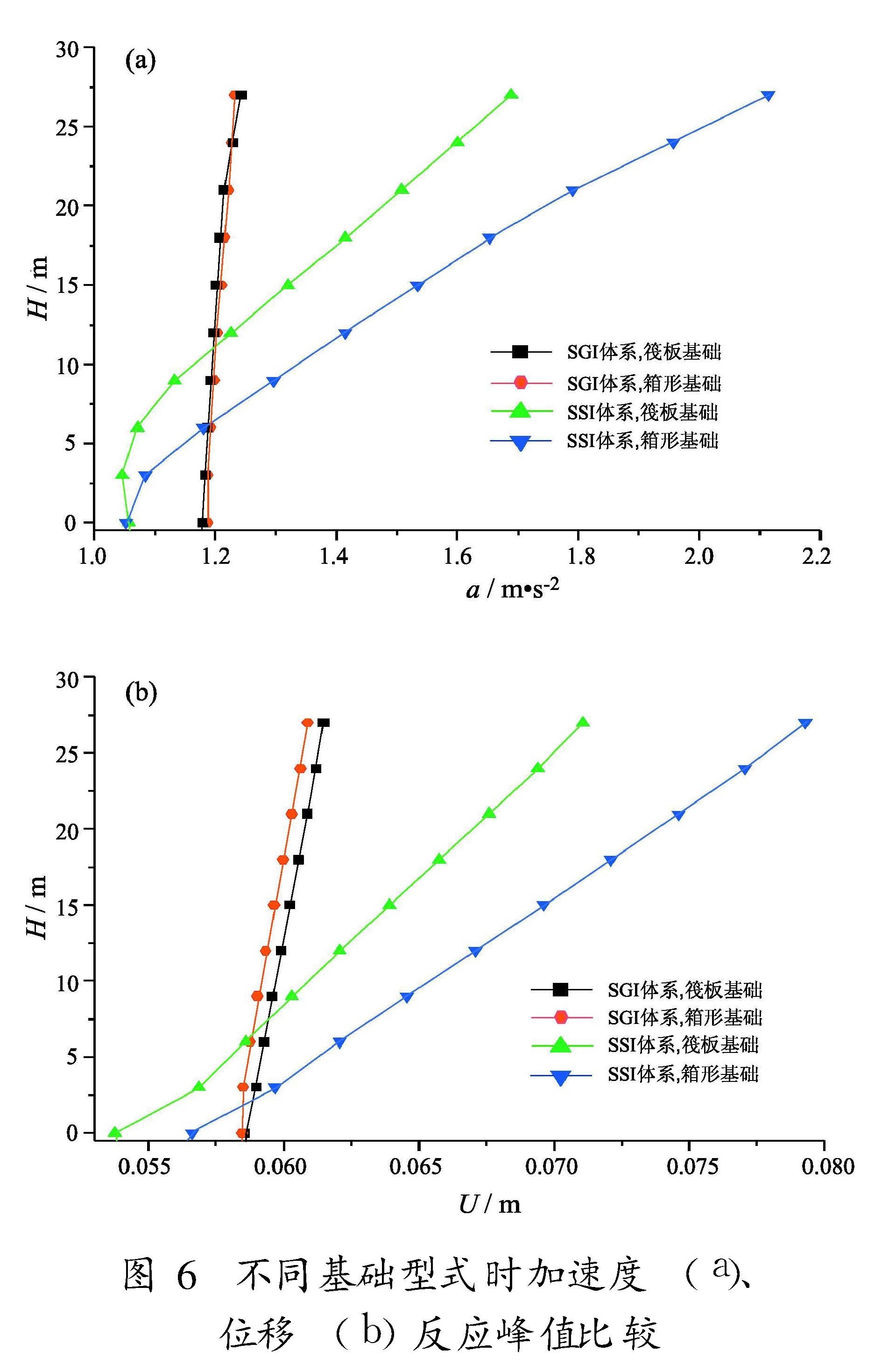
7.4 基础型式的影响为研究基础型式对SGI体系地震反应的影响,分别采用筏板基础和箱形基础进行对比分析,图6
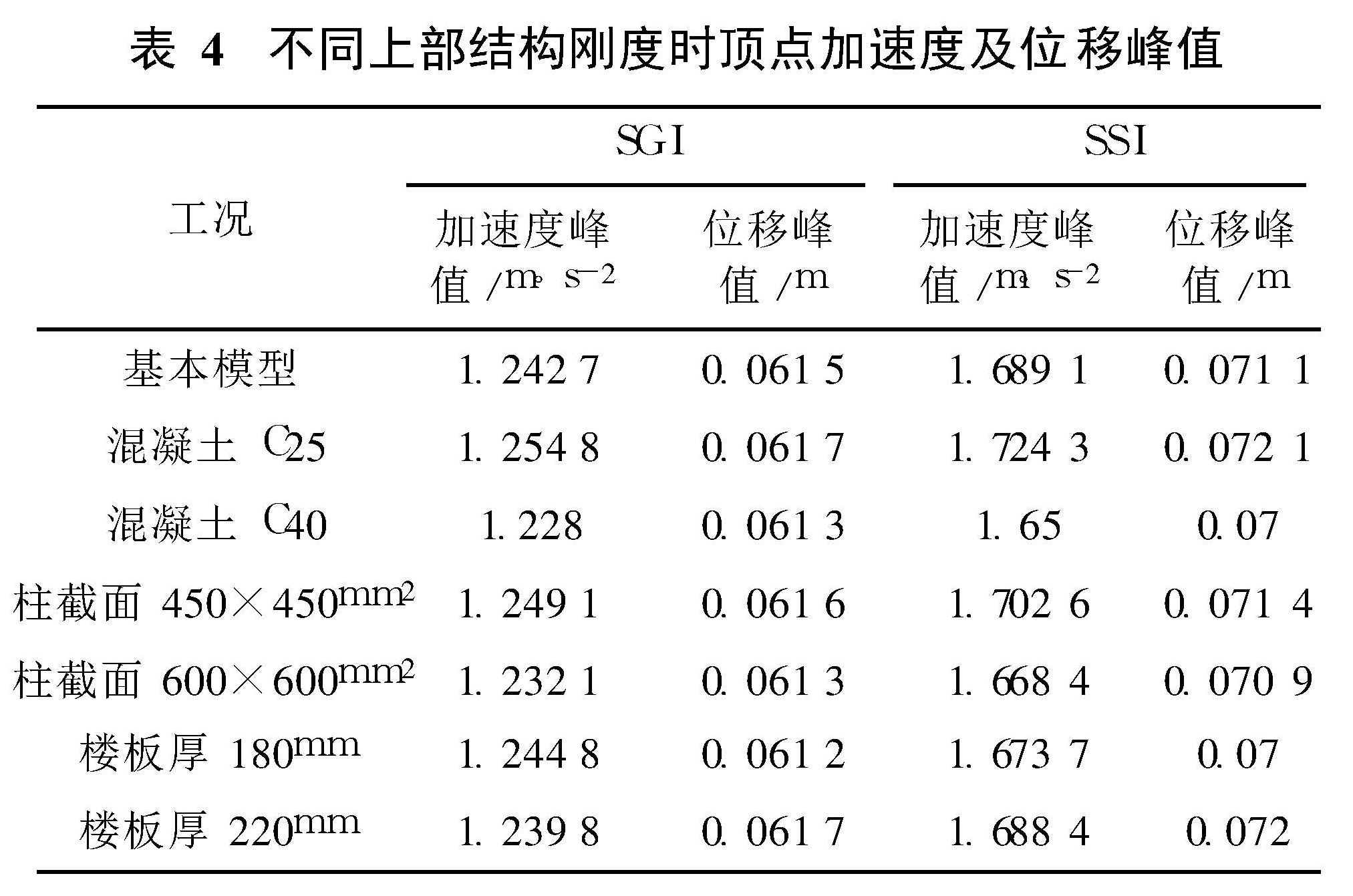
为不同基础型式时加速度及位移反应峰值对比。由图可见,由于隔震层的作用,基础型式对SGI体系上部结构地震反应的影响明显小于对非隔震的SSI体系地震反应的影响。本例中,箱基和筏基时SGI的加速度及位移反应峰值几乎相同。7.5 上部结构刚度的影响不同上部结构刚度时SGI、SSI体系加速度及位移反应峰值沿高度的变化规律与改变筏板厚度时类似。由于篇幅所限,本文仅给出各工况顶点加速度及位移峰值(表4)。
不同混凝土强度等级时,SGI体系加速度及位移反应峰值沿楼层的变化:随上部结构混凝土强度等级的增加,SGI体系加速度及位移反应均有所减小,但幅度很小,比SSI体系还小,混凝土由C25增加为C40时,顶点加速度及位移变化均未超过5%。
不同楼板厚度时,SGI体系加速度及位移反应峰值沿楼层的变化:随楼板厚度增加,SGI体系加速度反应峰值几乎未变,位移反应峰值有所增加,但幅度亦不大,比SSI体系还小,楼板厚度由180 mm增加到220 mm时,顶点加速度及位移峰值变化均未超过5%。
不同柱截面时,SGI体系加速度及位移反应峰值沿楼层的变化:随柱截面增大,加速度及位移反应峰值均有所减小,但幅度亦不大,柱截面由450 mm×450 mm增加到600 mm×600 mm时,顶点加速度及位移峰值变化均未超过5%。
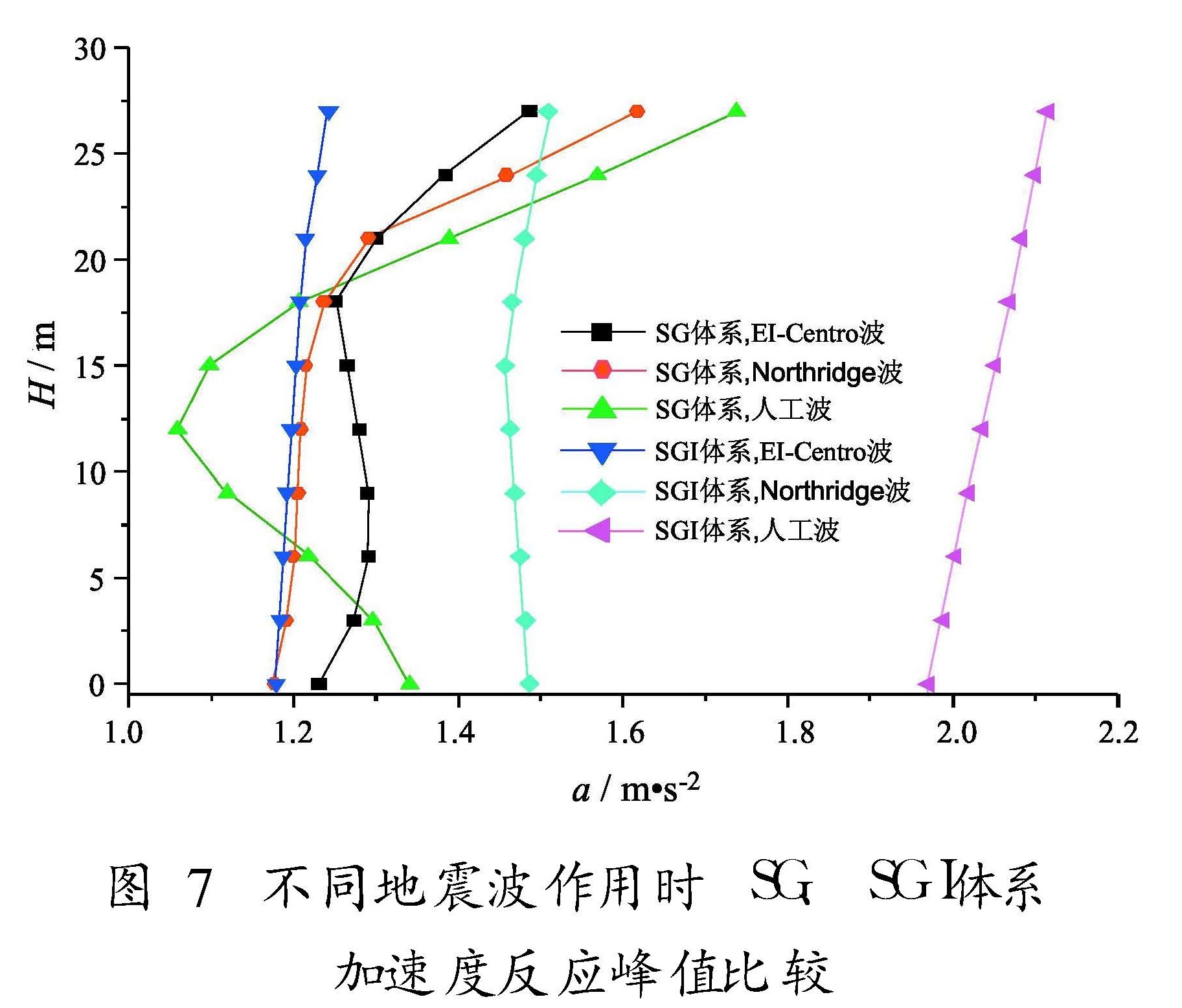
7.6 地震波的影响用选取的3条地震波分别作用于SG、SGI体系,然后进行计算分析。由于篇幅所限,本文仅给出加速度反应峰值沿高度的变化(图7)。对比分析可见:不同地震波作用下,不同体系地震反应有较大不同,与常规设计SG体系的地震反应规律亦不同。加速度反应El-Centro波作用最小,人工波作用最大,顶点加速度反应峰值二者相差达70.2%; 位移反应Northridge波作用最小,人工波作用最大,顶点位移反应峰值二者相差达88.2%。层间加速度及位移均较小。
8 结论
总结上述对隔震板柱结构—基础—地基动力相互作用及其影响因素的分析,可以得到如下结论:
(1)土层特性、基底埋深、土体深度对SGI体系地震反应影响明显。值得注意的是,虽然考虑土—结构相互作用后,影响内力反应的最大加速度减小,但结构的某些部位的内力却是增加的(边轴柱轴力、角柱剪力及弯矩增加),常规设计在这些部位的结果存在不安全隐患。
(2)上部结构刚度、筏板刚度、基础型式对SGI体系地震反应影响很小,本例顶点加速度及位移反应峰值变化均未超过5%。因此,从动力相互作用的角度讲,对隔震板柱体系一味增加上部结构和基础刚度并不能获得理想的抗震效果。
(3)土阻尼比对SGI体系地震反应的影响大于上部结构阻尼比的影响。由于隔震层的作用,相对于SSI体系,这种影响对SGI体系明显降低。若对土和上部结构采用相同阻尼比,将得到偏于安全的结果。
- 鲍华,徐礼华,徐书平,等.2005.土—结构相互作用对基础隔震体系地震反应的影响[J].工业建筑,(8):75-81.
- 董建国,赵锡宏.1997.高层建筑地基基础——共同作用理论与实践[M].上海:同济大学出版社.
- 窦立军,杨柏坡,刘光和,等.1999.土—结构动力相互作用几个实际应用问题[J].世界地震工程,(4):62-68.
- 孙树民.2001.土—结构动力相互作用研究进展[J].中国海洋平台,(5~6):31-36.
- 熊辉,邹银生,许振宇,等.2004.层状场域内桩—土—上部结构的整体动力有限元模拟[J].土木工程学报,(9):55-61.
- 张卫东.2006.隔震板柱结构非线性地震响应分析[J].低温建筑技术,(6):42-44.
- 张卫东.2007.板柱结构—基础—地基共同作用分析[J].四川建筑科学研究,(6):109-112.
- 张卫东.2007.隔震板柱结构LRB参数研究[J].低温建筑技术,(4):65-67.
- 邹立华,赵人达,赵建昌,等.2004.桩—土—隔震结构相互作用地震响应分析[J].岩土工程学报,(6):782-786.
- Deeks A J,Randolph M F.1994.Axisymmetric time-domain transmitting boundaries[J].J.of Eng.Mechanics,120(1):25-42.