基金项目:天津市科技支撑计划重点项目(09ZCKFSF00700)资助.
(1.内蒙古农业大学,呼和浩特 010018; 2.中国地震局地壳应力研究所,北京 100085; 3.天津市地震局,天津 300201)
(1.Inner Mongolia Agriculture University,Huhhot 010080,Inner Mongolia,China)(2.Institute of Crustal Dynamics,CEA,Beijing 100085,China)(3.Earthquake Administration of Tianjin Municipality,Tianjin 300201,China)
Earth tide; oceanic tide loading; M2 wave; tide factor; phase shift
备注
基金项目:天津市科技支撑计划重点项目(09ZCKFSF00700)资助.
应用Schwiderski全球海潮模型,采用积分格林函数方法计算了海潮M2波的应变负荷潮。通过调和分析和残差计算,对京、津、唐地区的7个承压水位观测井的水位固体潮M2波进行了海潮负荷改正。计算结果显示,观测井水位M2波潮汐因子和相位漂移的标准偏差分别由改正前的2.263和24.57°降低到0.898和3.58°。
Applying the Schwiderski model of global ocean tides and the method of Green function integral,we conduct the harmonic analysis and residual calculation of the water-level-tide M2 wave observed by seven pressure wells in Beijing,Tianjin and Tangshan.The result shows that the standard deviation of tide factor shifts from 2.263 to 0.898 and the standard deviation of phase shifts from 4.57° to 3.58° after the oceanic tide loading correction.
引言
太阳和月亮的引力使得地球发生周期性整体变形,这种变形称为地球固体潮。由于地球固体潮的作用,地下含水层发生周期性变形,使含水层水头压力发生周期性变化。承压、封闭性好的井—含水层系统可以记录到水位固体潮。地球对海潮负荷产生的响应称为海潮负荷潮,它在沿海地区非常显著。一般情况下,沿海地区重力负荷潮约占重力固体潮的10%~20%(Lambert et al,1998),应变负荷潮约占应变固体潮的25%,地倾斜负荷潮约占地倾斜固体潮的90%(吴庆鹏,1997; 周江存等,2006)。
近年来,人们在探求地壳运动、构造异常和物质变化(如海洋潮汐)引起的重力、倾斜和应变与地震之间的关系方面取得了许多成果(张国安等,2004)。在海洋潮汐对重力、倾斜和应变的影响研究方面,孙和平等(2005)通过对海潮和固体潮模型的适定性研究,提出了计算台站平均观测残差和剩余残差矢量的“非等权均值法”; 通过对周日和半日频段内的重力潮汐参数实施负荷改正,提出了“负荷改正有效性”概念。周江存等(2002)研究了我国台湾地区10个台站的重力、位移、倾斜和应变固体潮观测中的海潮负荷效应。王勇等(2003)讨论了绝对重力观测中的潮汐改正问题,重点对绝对重力观测中的海潮负荷影响进行了研究。为了提高GPS定位的精度,陈宪冬(2006)根据测站位移的海潮负荷改正理论,计算了部分IGS站的海潮负荷改正值。
近年来,人们普遍关注重力、倾斜和应变的海潮负荷研究,但对承压井水位的海洋潮汐响应研究得不多(张昭栋,郑金涵,1990)。在地下水微动态监测中,根据井水位固体潮的异常变化(畸变)可以识别出地震前兆或地下脉动信息(夏菲,万登堡,1992; 万登堡,夏菲,1995; 陆明勇等,2006),但在沿海地区,由于海潮负荷效应的影响,难以有效地识别地下水位微动态中的地震前兆信息。因此,在分析沿海地区的固体潮观测资料时,剔除海潮负荷的影响就显得十分重要。本文利用Schwiderski全球海潮模型,采用积分格林函数方法对京、津、唐地区承压井水位固体潮M2波进行海潮负荷改正,取得了较好的效果。
1 Schwiderski海潮模型
Schwiderski(1980)利用2 000多个沿海和海岛上的海潮观测结果作为限制条件,把全球海洋分成1°×1°的网格,求解考虑上述诸因素的潮汐运动方程。将洋面上任意一点潮汐分波的运动表示成余弦波的形式,就可得出描述某潮汐波运动的两个参数,它的振幅ξai和格林尼治相位滞后δi(θ,λ)在每个网格上的数值,即对第i个潮汐波有
ξi=ξaicos(ωit-δi)=Re(ξaie-iδieiωit),
ωi=ni·a.(1)
其中,ξi为第i个海潮潮汐波于t时刻在(θ,λ)点的潮高,ni为由第i个潮汐波的杜森编码构成的行向量; a为由世界时t时刻的6个天文参数τ、s、h、p、N'、ps构成的列向量; ωi为第i个潮汐波的角频率; θ、λ分别为水质点所在位置的余纬和经度。令
Hi(θ,λ)=ξaie-iδi.(2)
Hi(θ,λ)与时间无关,可以把它看成是决定于海潮分波的振幅ξai和初相位滞后δi的复潮高。Schwi-derski(1980)根据其计算结果给出了描述海洋潮汐运动的8个主要潮汐波M2、S2、K2、K1、O1、P1、Q1、Mf的海潮图。根据这8个海潮图可以计算出海洋上任意一点任意时间的海潮潮高。
2 积分格林函数方法
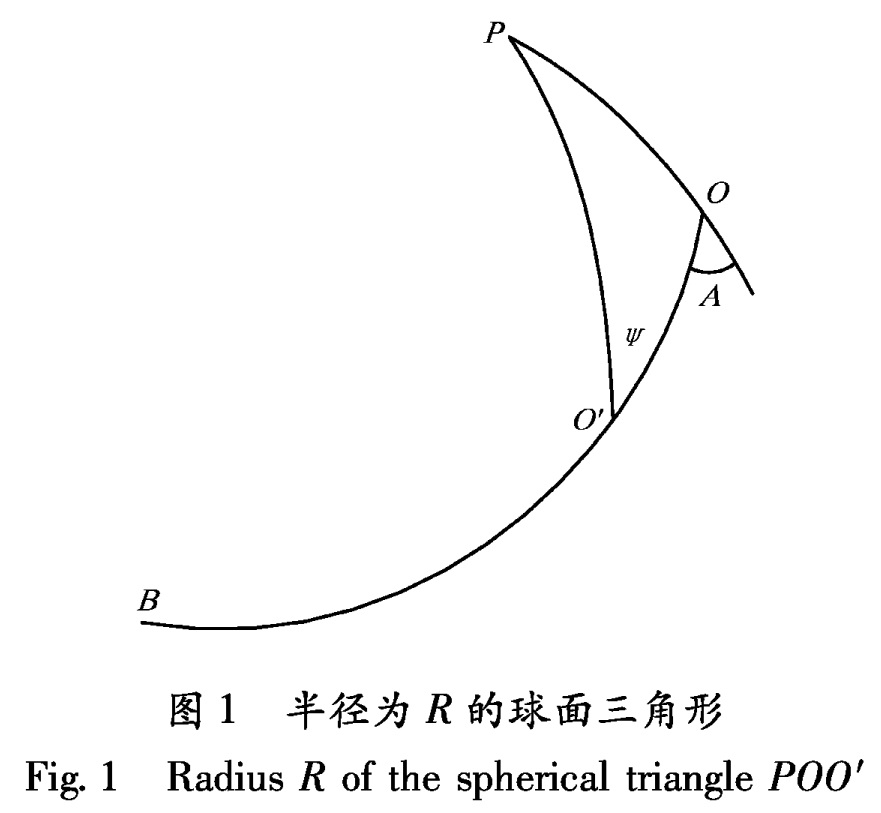
图1中,POO'为半径为R的球面上的球面三角形,P为北极; O(θ,λ)为地面上的任意一点; O'(θ',λ')为海潮负荷点; ψ、A为以O点为极点的海潮负荷点O'的坐标; ψ为O、O'两点之间的球面距离; A为O'(ψ,A)点相对于O(0,0)的自南向西算起的方位角。若B为O点的对跖点,则根据单位点源面负荷的应变负荷格林函数的定义,位于宽度为dA的球面梯形OO'B上的海潮在O点产生的复负荷潮为
dL(O)=R2ρH(O')G(ψ)sinψdψdA.(3)
其中,ρ为海水的密度,H(O')为O点海潮的复潮高,G(ψ)为点源负荷格林函数。令
I(ψ)=R2∫G(ψ)sinψdψ.(4)
I(ψ)为积分负荷格林函数(吴庆鹏,1997)。
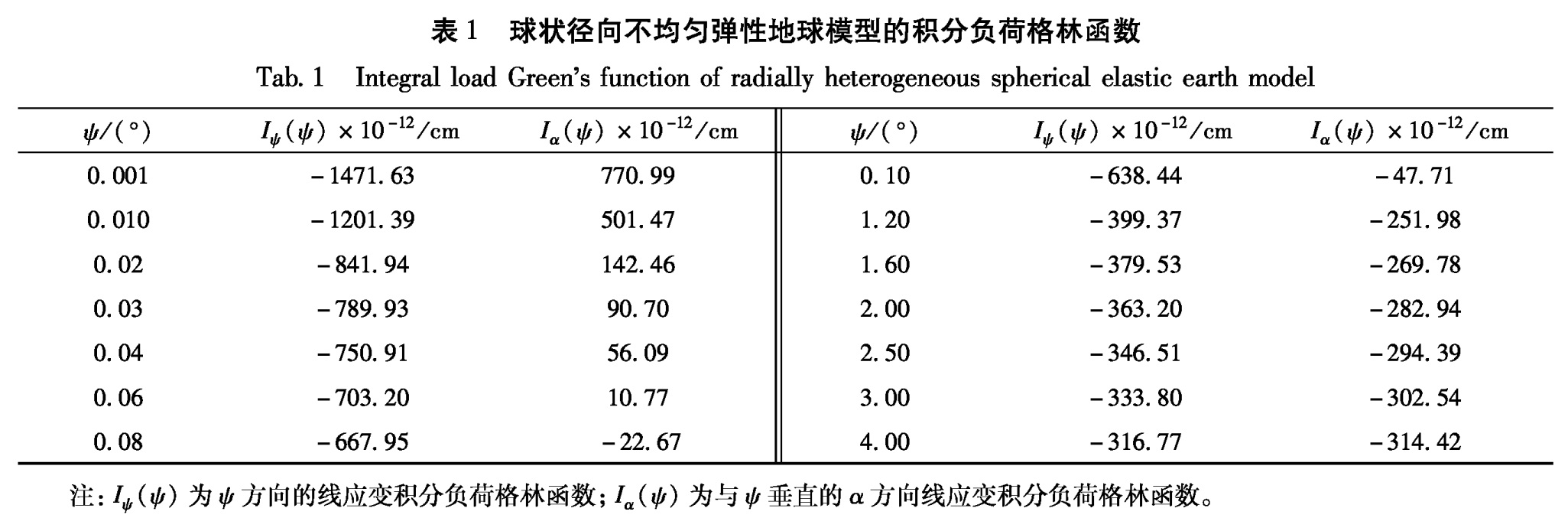
若把位于ψi、ψi+1之间的海潮复潮高H(O')看成常数,根据积分格林函数I(ψ)的定义和n阶勒让德多项式Pn(cosθ)积分公式,可以计算出地球模型的应变积分负荷格林函数(表1)。表1 球状径向不均匀弹性地球模型的积分负荷格林函数
Tab.1 Integral load Green's function of radially heterogeneous spherical elastic earth model注:Iψ(ψ)为ψ方向的线应变积分负荷格林函数; Iα(ψ)为与ψ垂直的α方向线应变积分负荷格林函数。
已知地球模型的线应变积分负荷格林函数,根据公式(3),就可得到全球海潮在地面上任一点产生的复应变负荷潮NS向分量εθθ、EW向分量ελλ和切变分量ελθ的计算公式
εθθ(O)=∫[∑iHiΔIψ(ψi)]cos2AdA+∫[∑iHiΔIα(ψi)]sin2AdA,
ελλ(O)=∫[∑iHiΔIψ(ψi)]sin2AdA+∫[∑iHiΔIα(ψi)]cos2AdA,
ελθ(O)=∫[∑iHi(ΔIψ(ψi)-ΔIα(ψi))]sinAcosAdA.(5)
3 海潮负荷计算
笔者以京、津、唐地区(38.6°~40.4°N,116.1°~119.2°E)作为研究区,分别在山前平原区、中部平原区和滨海平原区3个水文地质单元中选取7个承压含水层水位观测井进行海潮负荷计算。
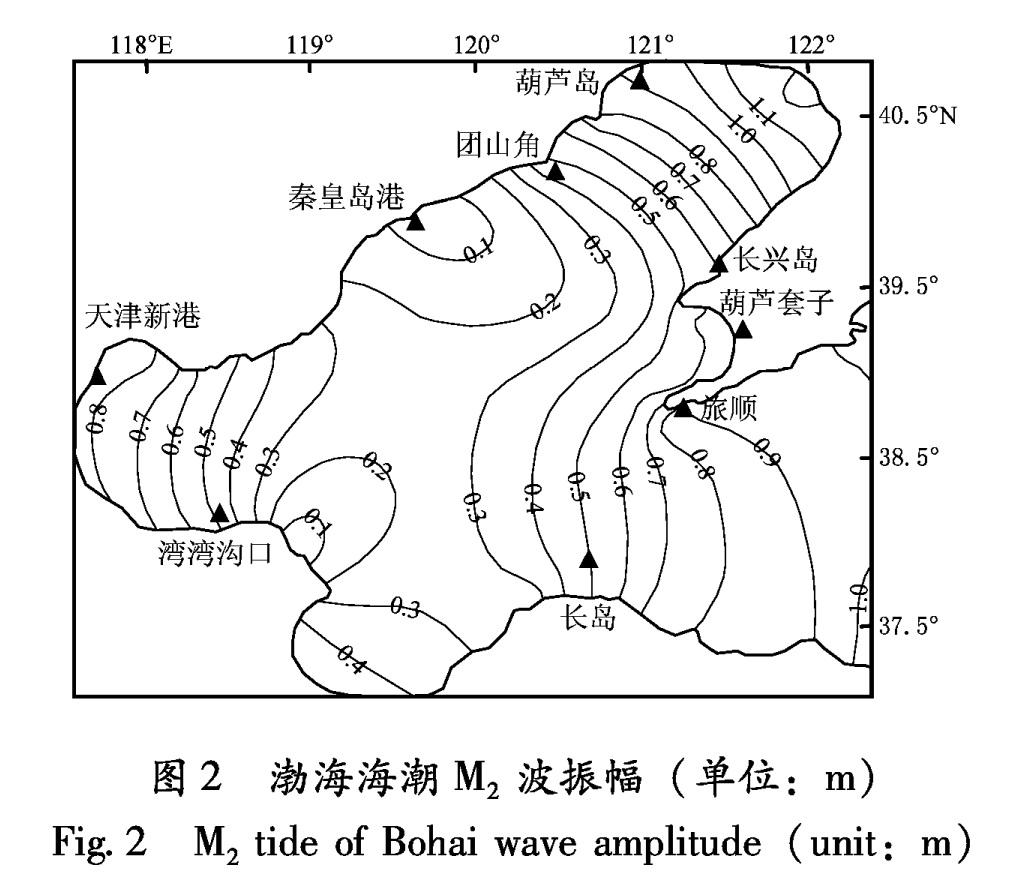
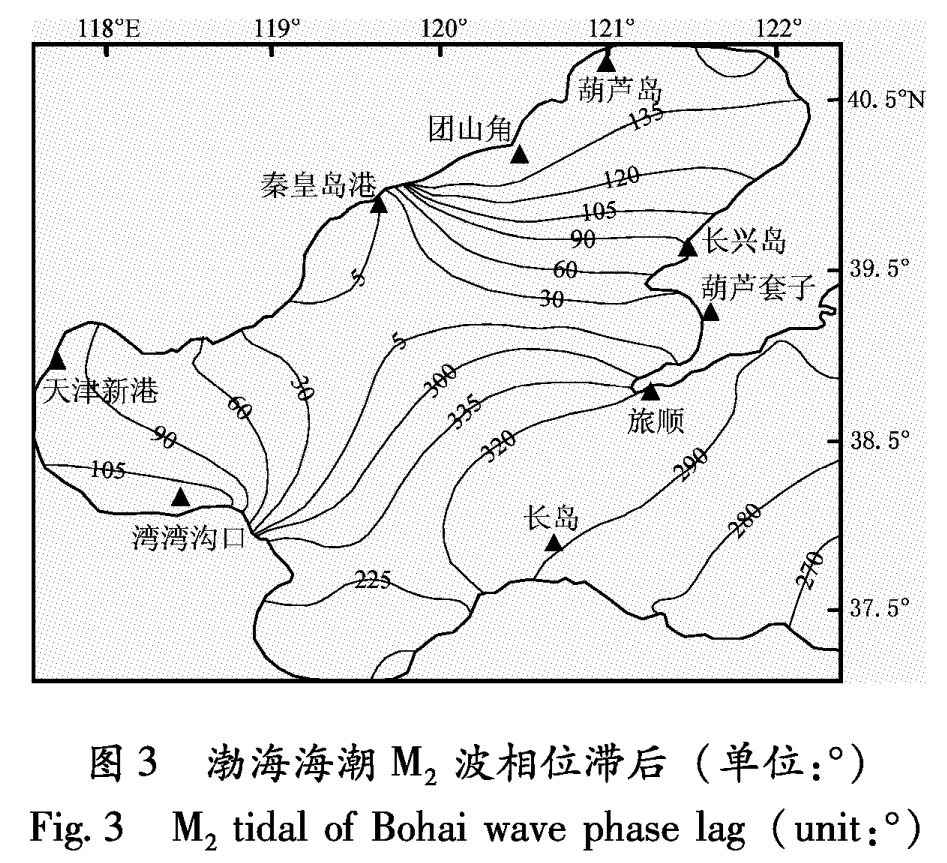
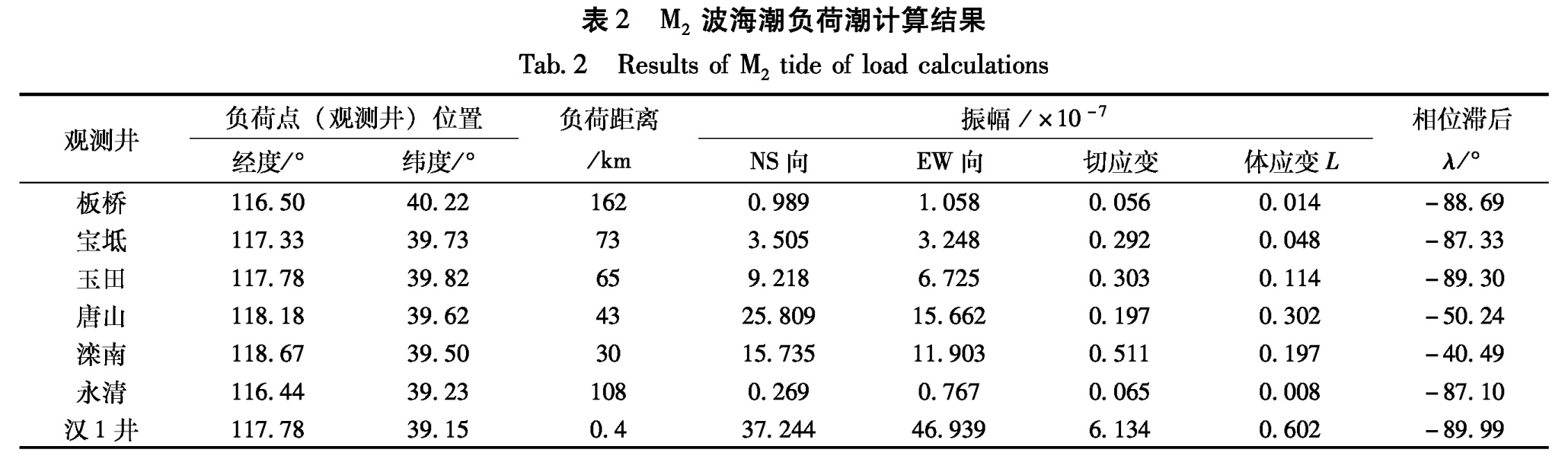
笔者以渤海海域(38.4°~39.0°N,117.8°~119.0°E)作为海潮负荷区域,以38.7°N,118.4°E点为海潮负荷点。根据李艳芸和李绍武(2006)利用Coherens模型计算给出的渤海海潮图(图2、图3)以及公式(1)和公式(5),笔者计算了研究区7个水位观测井的M2波海潮负荷矢量振幅L和相位滞后λ(表2)。
图2 渤海海潮M2波振幅(单位:m)
Fig.2 M2 tide of Bohai wave amplitude(unit:m)图3 渤海海潮M2波相位滞后(单位:°)
Fig.3 M2 tidal of Bohai wave phase lag(unit:°)表2 M2波海潮负荷潮计算结果
Tab.2 Results of M2 tide of load calculations4 海潮负荷改正
4.1 水位调和分析对观测井水位进行调和分析时,用来比较的基准是体应变固体潮。起潮力在观测井内引起的水位变化与观测井所在位置的应变固体潮理论值之比称为潮汐因子(汪成民等,1988)。我们采用维涅第科夫方法对研究区观测井水位固体潮观测资料进行调和分析。
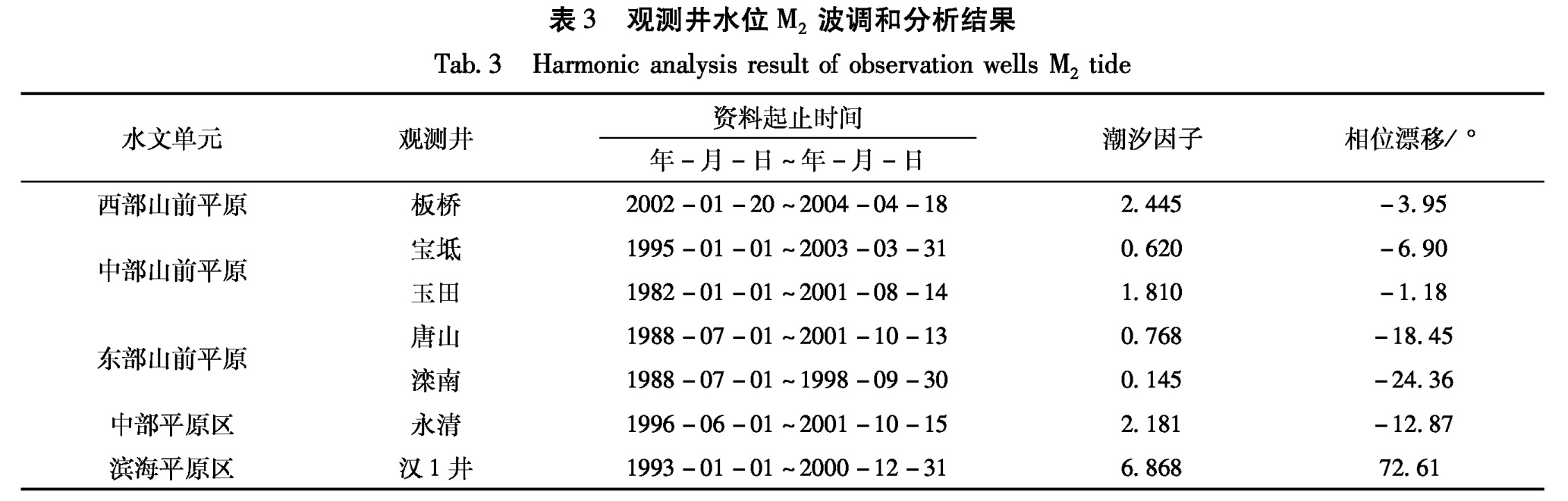
笔者首先对观测资料进行完整性和一致性处理,从而消除因观测条件变化引起的系统误差,用3次样条插值法将观测仪器故障等原因造成的间断补齐,然后对观测资料进行气压订正。在此基础上,根据滤波理论把日波和半日波分开,再用最小二乘法解线性方程组,从半日波中分离出M2波信号,并求出其潮汐因子和相位差(表3)。
表3 观测井水位M2波调和分析结果
Tab.3 Harmonic analysis result of observation wells M2 tide观测井水位固体潮调和分析结果表明,研究区7个观测井水位M2波平均相位漂移为20.05°,其中靠近渤海的东部山前平原区的唐山井和滦南井、中部平原区的永清井和滨海平原区的汉1井相位漂移明显(表3),尤其是汉1井(距海岸线仅400 m)相位漂移达+72.61°。经过海潮负荷改正后,平均相位漂移降低到6.62°,标准偏差由24.57°降低到3.58°。海潮负荷改正前,观测井水位M2波潮汐因子的标准偏差为2.263,负荷改正后降低到0.898。
4.2 残差及负荷改正观测残差矢量是指从水位观测潮波矢量中扣除相应的理论值得到的结果,其物理意义是检验地球模型的适应性。它的值越小,说明所采用的地球潮汐模型越接近于实际情况(孙和平,许厚泽,1999)。根据矢量图解原理,用M2分波形式表示的观测残差矢量的振幅B和相位β分别为
B=Aδcos2φ(1+(δth/δ)2-2(δth/δ)cosα)1/2,
β=arctan(δsinα/δcosα-δth). (6)
式中,A为M2分波理论振幅(A=0.981 2); α为水位相位滞后值; δ为水位观测振幅; δth为体应变理论振幅; φ为观测点纬度。
剩余残差矢量是指从观测残差矢量中扣除海洋负荷矢量后剩余的部分。剩余残差矢量值越小说明观测残差矢量中的海潮负荷成份扣除得越彻底。由矢量图解原理求得其振幅X和相位τ的公式为
X=(B2+L2-2BLcos(β-λ))1/2,
τ=arctan[(Bsinβ-Lsinλ)/(Bcosβ-Lcosλ)]. (7)
经海潮负荷改正后的潮汐振幅因子δ'和相位滞后Δφ的计算公式为
δ'=δth(1+(X/Aδth)2+2(X/Aδth)cosτ)1/2
Δφ=arctan[Xsinτ/(Aδth+Xcosτ)]. (8)
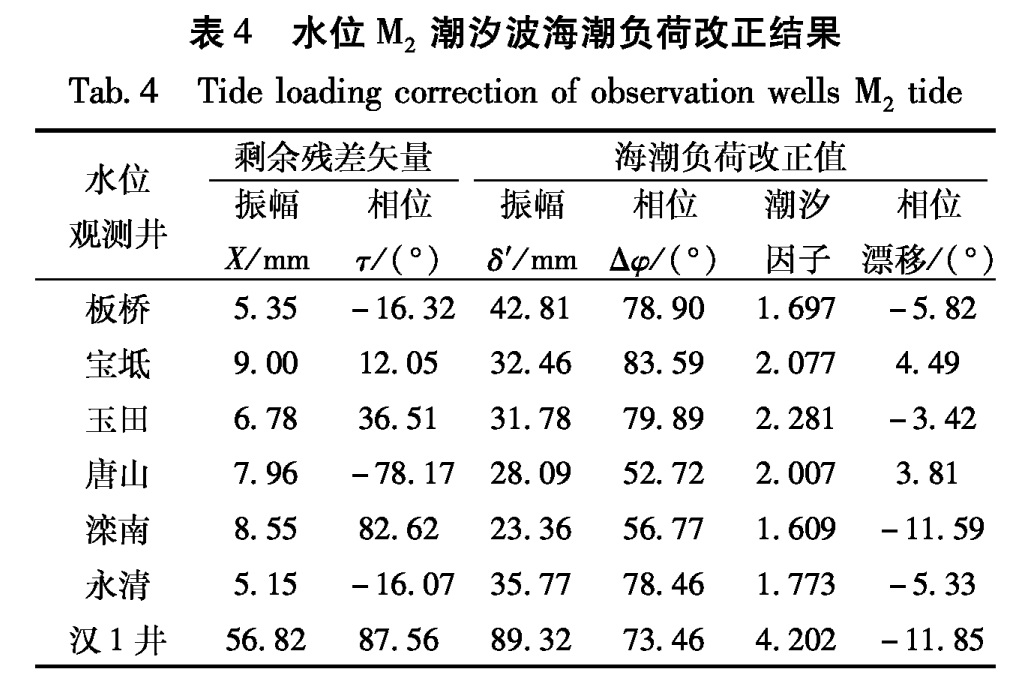
表4给出了研究区各观测井水位M2潮汐波海潮负荷改正结果。
表4 水位M2潮汐波海潮负荷改正结果
Tab.4 Tide loading correction of observation wells M2 tide5 讨论
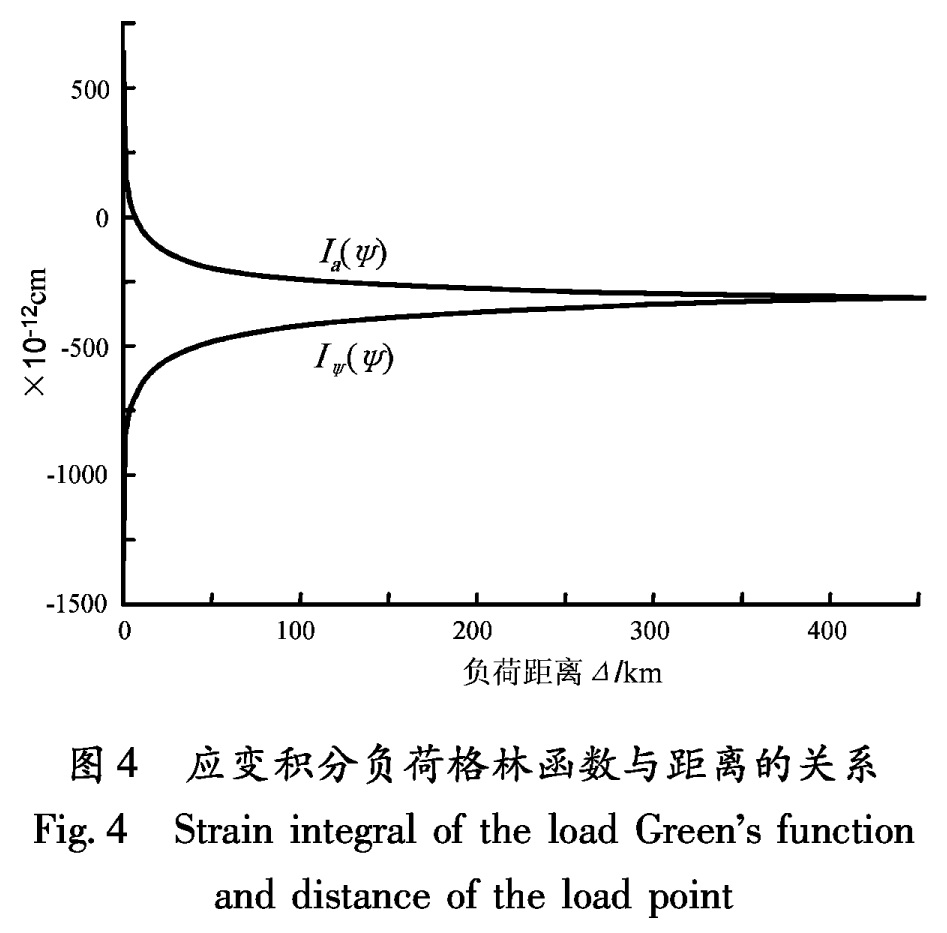
根据球状径向不均匀弹性地球模型理论,海潮负荷效应包括海水质量周期性涨落引起的直接效应和地球弹性形变导致的负荷效应。从应变积分负荷格林函数与负荷距离的关系可以看出,当Δ≤100 km时,Iψ(ψ)与Iα(ψ)呈反向非线性变化(图4); 当Δ>100 km时,随着Δ的增大,Iψ(ψ)与Iα(ψ)呈线性变化并逐渐趋于一致。说明当Δ≤100 km时,海潮负荷直接效应占主导地位; Δ>100 km时,地球弹性形变负荷效应占主导地位。
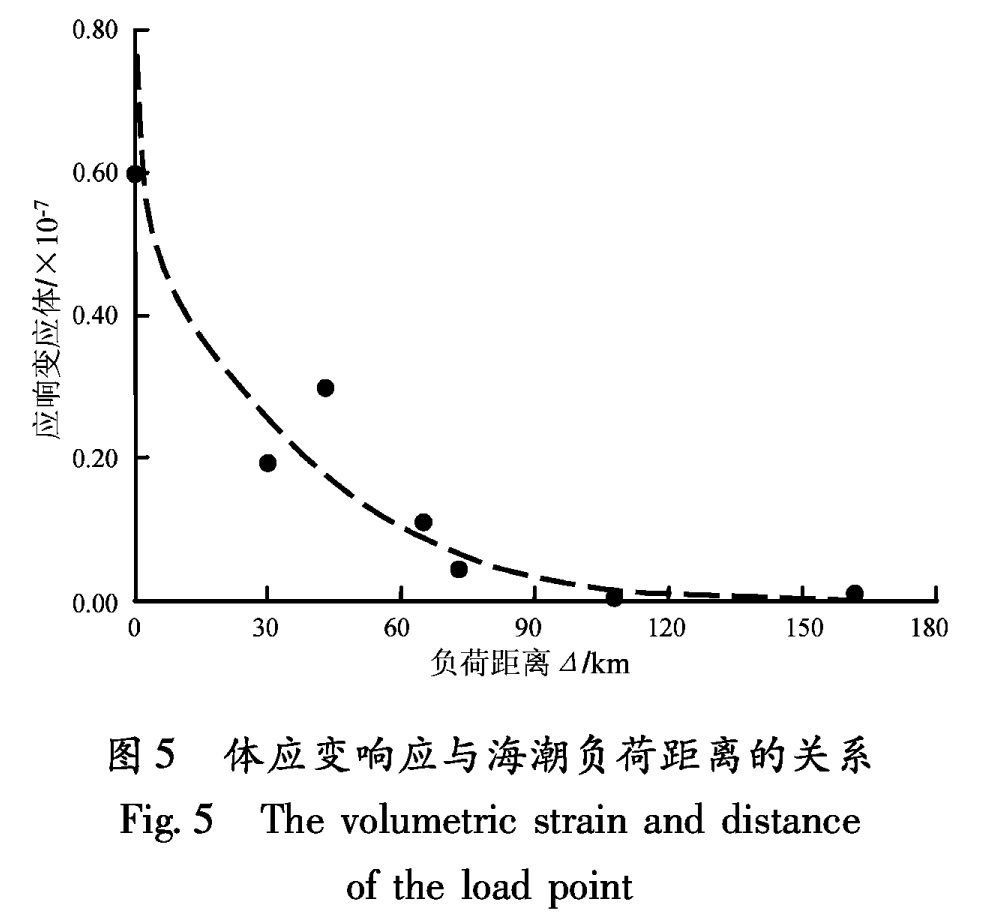
海潮负荷的体应变响应与距离有着密切关系。在Δ≤30 km范围内,体应变响应随着Δ的减小迅速增大(图5); 在Δ=30~90 km范围内,随着Δ的增大体应变响应逐渐减小; 当Δ>100 km时,体应变响应明显减弱。不难看出,在沿海地区(Δ≤30 km)海潮负荷效应对地下水微动态观测影响较大,可能会直接干扰甚至淹没水位固体潮的微动态信息。图4 应变积分负荷格林函数与距离的关系
Fig.4 Strain integral of the load Green's function and distance of the load point
6 结论根据体应变响应与海潮负荷距离的关系,海潮负荷对玉田井的影响大于永清井,但从计算结果看,永清井对海潮负荷的响应大于玉田井,这种现象可能与不同水文单元含水层的岩性和结构变化有关。剩余残差矢量的计算结果显示,除汉1井外,各观测井的水位M2波剩余残差矢量振幅X≤9.00 mm,说明观测残差矢量中的海潮负荷成份扣除得比较彻底。
参考文献:
陈宪冬.2006.GPS精密定位中的海潮负荷改正[J].西南交通大学学报,41(4):429-432.
李艳芸,李绍武.2006.风暴潮预报模式在渤海海域中的应用研究[J].海洋技术,25(1):101-106.
陆明勇,牛安福,白长清,等.2006.地壳形变短临异常与地下水位短临异常关系及识别方法的初步研究[J].地震研究,29(1):13-20.
孙和平,Ducarme B,许厚泽,等.2005.基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J].中国科学(D辑),35(7):649-657.
孙和平,许厚泽,周江存,等.2005.武汉超导重力仪观测最新结果和海潮模型研究[J].地球物理学报,48(2):299-307.
孙和平,许厚泽.1999.用超导重力仪的潮汐观测资料研究海潮模型[J].测绘学报,28(2):115-120.
万登堡,夏菲.1995.云南地下水位动态短临标志体系研究[J].地震研究,18(3):282-293.
汪成民,车用太,万迪堃,等.1988.地下水微动态研究[M].北京:地震出版社.
王勇,张为民,王虎彪,等.2003.绝对重力观测的潮汐改正[J].大地测量与地球动力学,23(2):65-68.
吴庆鹏.1997.重力学与固体潮[M].北京:地震出版社.
夏菲,万登堡.1992.井潮系数、气压系数与地震关系的探讨[J].地震研究,15(1):29-35.
张国安,徐菊生,王秀君.2004.固体潮观测与研究的国际动态与进展[J].地震研究,27(1):104-110.
张昭栋,郑金涵.1990.承压井水位对地表水潮汐的响应[J].地震研究,13(4):377-388.
周江存,孙和平,李正媛.2006.佘山台倾斜固体潮观测的海潮负荷改正[J].测绘学报,35(1):4-8.
周江存,许厚泽,孙和平.2002.中国台湾地区海洋负荷潮汐对重力、位移、倾斜和应变固体潮观测的影响[J].大地测量与地球动力学,22(1):83-88.
Lambert A,Pagiatakis S D,Billyard A P,et al≤9.00 mm,说明观测残差矢量中的海潮负荷成份扣除得比较彻底。
- 陈宪冬.2006.GPS精密定位中的海潮负荷改正[J].西南交通大学学报,41(4):429-432.
- 李艳芸,李绍武.2006.风暴潮预报模式在渤海海域中的应用研究[J].海洋技术,25(1):101-106.
- 陆明勇,牛安福,白长清,等.2006.地壳形变短临异常与地下水位短临异常关系及识别方法的初步研究[J].地震研究,29(1):13-20.
- 孙和平,Ducarme B,许厚泽,等.2005.基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J].中国科学(D辑),35(7):649-657.
- 孙和平,许厚泽,周江存,等.2005.武汉超导重力仪观测最新结果和海潮模型研究[J].地球物理学报,48(2):299-307.
- 孙和平,许厚泽.1999.用超导重力仪的潮汐观测资料研究海潮模型[J].测绘学报,28(2):115-120.
- 万登堡,夏菲.1995.云南地下水位动态短临标志体系研究[J].地震研究,18(3):282-293.
- 汪成民,车用太,万迪堃,等.1988.地下水微动态研究[M].北京:地震出版社.
- 王勇,张为民,王虎彪,等.2003.绝对重力观测的潮汐改正[J].大地测量与地球动力学,23(2):65-68.
- 吴庆鹏.1997.重力学与固体潮[M].北京:地震出版社.
- 夏菲,万登堡.1992.井潮系数、气压系数与地震关系的探讨[J].地震研究,15(1):29-35.
- 张国安,徐菊生,王秀君.2004.固体潮观测与研究的国际动态与进展[J].地震研究,27(1):104-110.
- 张昭栋,郑金涵.1990.承压井水位对地表水潮汐的响应[J].地震研究,13(4):377-388.
- 周江存,孙和平,李正媛.2006.佘山台倾斜固体潮观测的海潮负荷改正[J].测绘学报,35(1):4-8.
- 周江存,许厚泽,孙和平.2002.中国台湾地区海洋负荷潮汐对重力、位移、倾斜和应变固体潮观测的影响[J].大地测量与地球动力学,22(1):83-88.
- Lambert A,Pagiatakis S D,Billyard A P,et al≤9.00 mm,说明观测残差矢量中的海潮负荷成份扣除得比较彻底。 参考文献:
- 陈宪冬.2006.GPS精密定位中的海潮负荷改正[J].西南交通大学学报,41(4):429-432.
- 李艳芸,李绍武.2006.风暴潮预报模式在渤海海域中的应用研究[J].海洋技术,25(1):101-106.
- 陆明勇,牛安福,白长清,等.2006.地壳形变短临异常与地下水位短临异常关系及识别方法的初步研究[J].地震研究,29(1):13-20.
- 孙和平,Ducarme B,许厚泽,等.2005.基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J].中国科学(D辑),35(7):649-657.
- 孙和平,许厚泽,周江存,等.2005.武汉超导重力仪观测最新结果和海潮模型研究[J].地球物理学报,48(2):299-307.
- 孙和平,许厚泽.1999.用超导重力仪的潮汐观测资料研究海潮模型[J].测绘学报,28(2):115-120.
- 万登堡,夏菲.1995.云南地下水位动态短临标志体系研究[J].地震研究,18(3):282-293.
- 汪成民,车用太,万迪堃,等.1988.地下水微动态研究[M].北京:地震出版社.
- 王勇,张为民,王虎彪,等.2003.绝对重力观测的潮汐改正[J].大地测量与地球动力学,23(2):65-68.
- 吴庆鹏.1997.重力学与固体潮[M].北京:地震出版社.
- 夏菲,万登堡.1992.井潮系数、气压系数与地震关系的探讨[J].地震研究,15(1):29-35.
- 张国安,徐菊生,王秀君.2004.固体潮观测与研究的国际动态与进展[J].地震研究,27(1):104-110.
- 张昭栋,郑金涵.1990.承压井水位对地表水潮汐的响应[J].地震研究,13(4):377-388.
- 周江存,孙和平,李正媛.2006.佘山台倾斜固体潮观测的海潮负荷改正[J].测绘学报,35(1):4-8.
- 周江存,许厚泽,孙和平.2002.中国台湾地区海洋负荷潮汐对重力、位移、倾斜和应变固体潮观测的影响[J].大地测量与地球动力学,22(1):83-88.
- Lambert A,Pagiatakis S D,Billyard A P,98.Improved ocean tide loading corrections for gravity and displacement:Canada and Northern United States[J].Geophys Res,103(B12):30231-30244.
- Schwiderski E.1980.On charting global ocean tides[J].Rev Geophys Space Phys,18:243-268.