基金项目:国家科技支撑计划项目(2006BAG04B00)资助.
(1.长安大学 公路学院,西安 710064; 2.西南交通大学 土木工程学院,成都 610031)
(1.School of Highway,Chang'an University,Xi'an 710064,Shaanxi,China)(2.School of Civil Engineering,Southwest Jiaotong University,Chengdu 610031,Sichuan,China)
bridge engineering; stochastic vibration; cable-stayed bridge; earthquake motion; local site effect
备注
基金项目:国家科技支撑计划项目(2006BAG04B00)资助.
基于随机振动理论,以苏通长江公路大桥为例,研究了局部场地效应对大跨度斜拉桥地震反应的影响。结果 表明:与一致激励相比,局部场地效应对结构的内力和位移影响显著; 场地效应对主梁、索塔内力和位移的影响程度及规律也不尽相同,须区别对待分析。
With the growth of the main span of the cable-stayed bridges,the spatial effect of earthquake motion for the spatial structures becomes a new research topic.Based on stochastic vibration theory and taking the example of SuTong Yangtze River Highway Bridge,the stochastic seismic response of super-long-span,cable-stayed bridge under local effect is developed.The results indicate that the internal force and displacement are influenced obviously by local site effect than by the uniform excitation.For different responses of internal force and displacement of the girder and tower,the impact and the rules are different for seismic ground motion under local effect.Therefore,in view of different cases,the analyses would have different results.
引言
2008年5月12日,四川省汶川县发生8.0级特大地震,造成6 000多座桥梁受损,交通瘫痪,严重影响了灾后救援工作,人民的生命财产受到极大损失。国内外大地震一再证明了桥梁工程遭到破坏的严重后果,因此,研究大跨度桥梁抗震具有重要意义。近年来由于斜拉桥设计理论、施工方法和新材料研究取得重大发展,斜拉桥的主跨正在经历由几百米到近千米甚至上千米的发展,如日本多多罗大桥主跨890 m,湖北鄂东长江公路大桥主跨926 m,香港昂船洲大桥主跨1 018 m,苏通长江公路大桥主桥(以下简称苏通大桥)的主跨为1 088 m。随着斜拉桥跨度的不断增大,地震动力学问题也变得越来越复杂,但斜拉桥的震害实例很少,而且无规范可循。因此,研究斜拉桥结构地震效应具有重要意义。
目前,对大跨度斜拉桥动力性能的研究不少,而且主要集中在自振特性及确定性分析(即反应谱分析和时程分析)方面。本文根据斜拉桥地震响应分析的研究现状(杜修力,陈厚群,1994),基于随机振动理论,将地震动作为随机变量,建立地面加速度功率谱密度模型,研究世界第一跨斜拉桥苏通大桥在随机地震荷载激励下的响应和局部场地效应对超大跨度斜拉桥结构响应的影响规律,期望随机振动理论在复杂大型桥梁工程抗震中得到广泛的应用,为大跨度桥梁的抗震设计或行业规范的制定提供科学依据。
1 随机地震动场的模拟
对地震引起的地面运动场的准确模拟是进行结构随机地震反应分析的基础和前提,反言之,结构的地震反应分析必须以地震场地运动特性(幅值、频谱特性和持续时间)为依据。而地震动的空间变化有如下特点(杜修力,陈厚群,1994; 王光远等,1999):① 存在一个与场地条件和两点间距离相关的频率,地震波低于该频率的部分可以用波动理论很好地表述,而高于该频率的部分则适合于用随机理论方法描述; ② 地震动场两点间地震动的相关性与两点间距离和地震动频率成分密切相关; ③ 地震动场任意两点的空间变化程度依赖于地震的震源特征。空间地震动场的模型应尽可能体现上述特征,一般来说,已知地震动场的各点自功率谱,则各点互功率谱可以表示成
Sjk=(Sjj(ω)Skk(ω)ρjk(d,ω)eiωd/(Va(ω)))1/2.(1)
式中,Sjj(ω)、Skk(ω)为j、k两点自功率谱,ρjk(d,ω)为j、k两点地震动的相干函数,用于描述两点地震动相关程度,d为两点在地震动传播方向上的距离。
1957年,日本学者Kanai-Tajimi提出了过滤白噪声的随机地震动平稳功率谱模型,之后许多学者提出过改进模型,本文采用杜修力—陈厚群模型(林家浩等,2001; 屈铁军等,1996),其表达式为
SA(ω)=(1+4ξ2g(ω2)/(ω2g))/((1-(ω2)/(ω2g))2+4ξ2g(ω2)/(ω2g))·1/(1+(Dω)2)·
(ω4)/(ω2+ω20)·S0.(2)
其中,1/(1+(Dω)2)是低通滤波器,(ω4)/(ω2+ω20)是高通滤波器,ω0≈1.83,为低频拐角频率,D=1/28π,为与震源有关的参数,ωg、ξg分别为场地土的卓越频率和阻尼比。
2 随机地震反应分析方法
2.1 基于ANSYS/PSD的随机地震反应分析方法对于多自由度线性振动体系的地震反应分析,振型叠加法为最常用的方法。假定动力方程中的阻尼项为经典阻尼,结构的动力相对位移可以用振型广义坐标表示为{ufd(t)}=[φ]{y(t)},代入方程可得
y¨j+2ξjωjy·j+ω2jyj={Гj}T{u¨r},(j=1,2,3…n).(3)
式中,n为需要计算的振型数; yj为第j振型的广义位移; ωj、ξj为第j振型的自振圆频率和模态阻尼比; {Гj}为相应于基础激励的振型参与系数,可表达为
{Гj}=-([Mff][A]+[Mfr])T{φj}{Γj}.(4)
在非一致激励随机振动分析中,随机荷载是以功率谱密度函数的形式来施加的,其输入的PSD可采用下列通用形式:
S(ω)=[S11(ω)
C12(ω)-iQ12(ω)
C13(ω)-iQ13(ω)
… C12(ω)+iQ12(ω)
S22(ω)
C23(ω)-iQ23(ω)
… C13(ω)+iQ13(ω)
C23(ω)+iQ23(ω)
S33(ω)
… …
…
…
…]n×n.(5)
式中,Sii(ω)为自功率谱,Sij(ω)为互谱实部,Qij(ω)为互谱的虚部,2≤n≤10。
2.2 局部场地效应的模拟地震发生时,大跨度斜拉桥结构的各支承点由于受行波效应、局部场地效应和空间部分相干效应的影响,各支承处输入的地震波是不同的。
不同激励点间的场地是有差异的。屈铁军等(1996)对实测地震记录进行回归拟合,得到了不同激励点的自功率谱。公式为
ΔS0=0.2571×Δh-0.0124Δx.(6)
式中,ΔS0是任意测点间自功率谱参数的差值,单位为cm2/(rad·s2),Δh为点j、h的土层厚度差值,单位为m。Δx为两测点的震中距差,单位为m。根据上式就可以从一点的自功率谱求得传播方向的直线上场地另一点的自功率谱。它表征了场地上不同激励点间的局部场地效应。
2.3 结构峰值响应的计算对于桥梁工程人员来说,直接利用随机振动反应的各阶谱矩进行结构设计是非常困难的。而根据随机振动理论利用随机反应的结果(功率谱、方差等)来定量估计桥梁结构地震的响应,则便于随机振动方法在桥梁工程上的应用(周勇军等,2006; 解丽等,2008)。
目前已有不同的方法利用随机反应的各阶谱矩来估计结构的响应以便于工程设计,其中应用较普遍的方法是由Davenport提出的(林家浩等,2001)。随机反应绝对值X(t)在时间[0,T]内的最大值可表示为
Xm=max0≤t≤T〖JB<1|〗X(t)〖JB>1|〗.(7)
其均值和方差分别为
E(Xm)=γmσX; σ2Xm=Δ2mσ2X.(8)
式中:γm=(2ln(V0T))1/2+(05772)/((2ln(V0T))1/2),
Δm=π/((12ln(V0T))1/2),
其中γm为峰值因子,T为地震动持时。
V0=1/(π)(σX·)/(σX).(9)
式中,σ2X=E[X2(t)]=λ0,是随机反应X(t)的均方值,即0阶谱矩; σ2X·=E[X·2(t)]=λ2,是随机反应速度X·(t)的均方值,即2阶谱矩。
3 工程背景及有限元模型
3.1 工程背景苏通长江公路大桥位于长江下游,临近长江入海口,是目前世界上最大跨度的双塔双索面斜拉桥,主桥跨径为100 m+100 m+300 m+1 088 m+300 m+100 m+100 m。主桥钢箱梁共分为17种类型(A~O)、141个梁段,节段标准长度为16 m,边跨尾索区节段标准长度为12 m。塔柱采用倒Y形结构,分为下塔肢、中塔肢、上塔肢和横梁4部。中、下塔肢为钢筋混凝土结构,上塔肢为钢锚箱—混凝土组合结构,索塔高300.4 m。斜拉索为Φ7平行钢丝体系,全桥共34×8=272根斜拉索,主桥结构布置如图1所示。
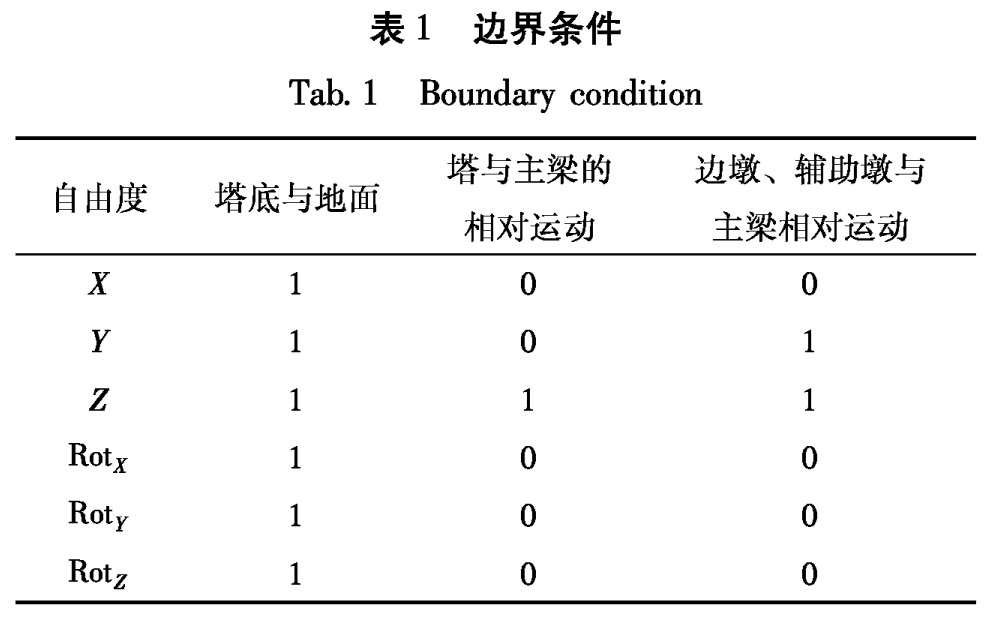
3.2 有限元模型及自振特性分析本文采用大型通用有限元分析软件ANSYS进行结构分析。有限元模型边界条件如表1所示,X轴表示桥轴向; Y轴为竖向; Z轴为横向,“1”表示约束; “0”表示自由。
在建立空间模型时,主要作了下列处理:
① 用“鱼刺梁”模拟主梁。主梁和索塔均采用beam44模拟; ② 斜拉索采用link8模拟; ③ 斜拉索与主梁之间的连接采用“鱼刺”与主梁连接,“鱼刺”用刚度很大(相对于主梁刚度)的beam4梁单元模拟; ④ 辅助墩及过渡墩采用beam44模拟; ⑤ 塔、墩底部的桩基础采用弹簧单元Combine14约束的方法模拟。
为了提高结构自振频率和振型的精度,笔者采用子空间迭代法计算结构的自振特性。限于篇幅,表2只列出了部分自振频率及相对应的振型特征。
斜拉桥的自振特性分析是研究斜拉桥动力行为的基础,其自振特性决定其动力反应的特性。从结构的频率变化和振型可以得出苏通大桥的动力特性如下:
① 自振周期长。苏通大桥的第一阶振动为纵向飘移,符合飘浮体系的特点,基本周期达13.2 s,为长周期,体现了该结构属于特柔性结构; ② 自振频率非常密集,频率变化均匀,无跳越现象,体现出苏通大桥结构动力特性的复杂性; ③ 振型表现出明显的三维性和相互耦合的特点,主梁、主塔和斜拉索之间相互影响,振动发生时,全桥振动体系中结合有各部分构件本身的振动。
4 局部场地效应分析
苏通长江公路大桥处于软土场地,按抗震烈度Ⅶ度进行设防,按场地类别为Ⅲ类。笔者选用杜修力模型,其震动模型参数取值如下(杜修力,1998; Zerva,1988,1991; 黄用军,王群,1997):S0=17.26 cm2/s3,D=0.0114,ω0=1.83,ωg=13.03,ξg=0.97,Tg=13.66。随机地震动输入功率谱曲线如图2所示。
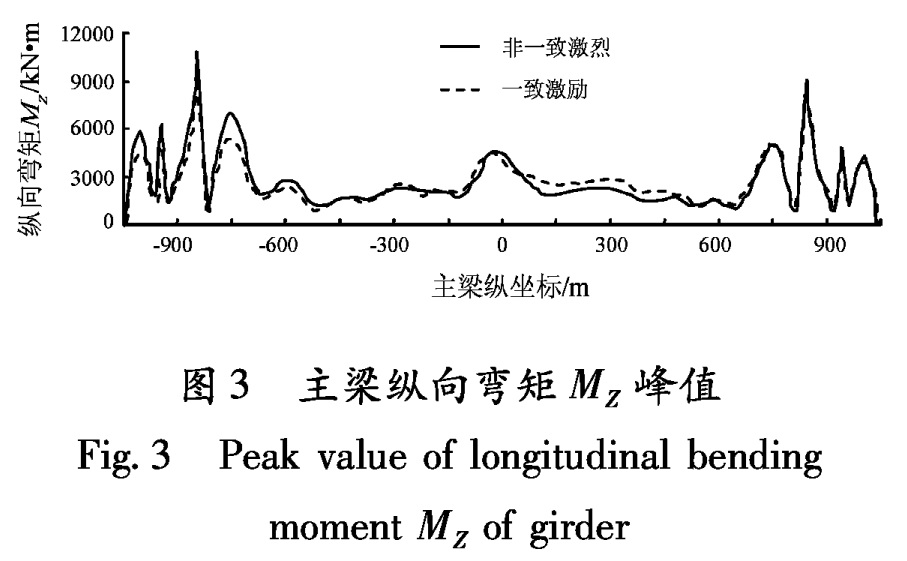
对于以上地震动输入,在ANSYS/PSD平台上采用CQC法计算各种响应的功率谱,然后按照随机振动理论求得内力及位移响应的均值和方差。为了保证较高的计算精度,考虑了前200阶振型参与贡献,阻尼比取值为5%,有效频率积分区间为ω∈[0.5,90.0] rad/s,积分间隔为0.05 rad/s。由于苏通大桥跨度比较大,若假定该桥各支承点的自功率谱相同,即忽略不同支承点间的场地差异,会存在很大的不合理性。根据地震地面运动空间变化的特点,分析苏通大桥在随机地震荷载作用下的动力响应需考虑局部场地效应。此处按Δh=0和Δx=1 088 m考虑北、南主塔支承处的场地差异。在计算分析过程中,在两个支承处输入有差异的自功率谱。局部场地效应对主梁和主塔内力及位移峰值的影响如图3至图5所示。
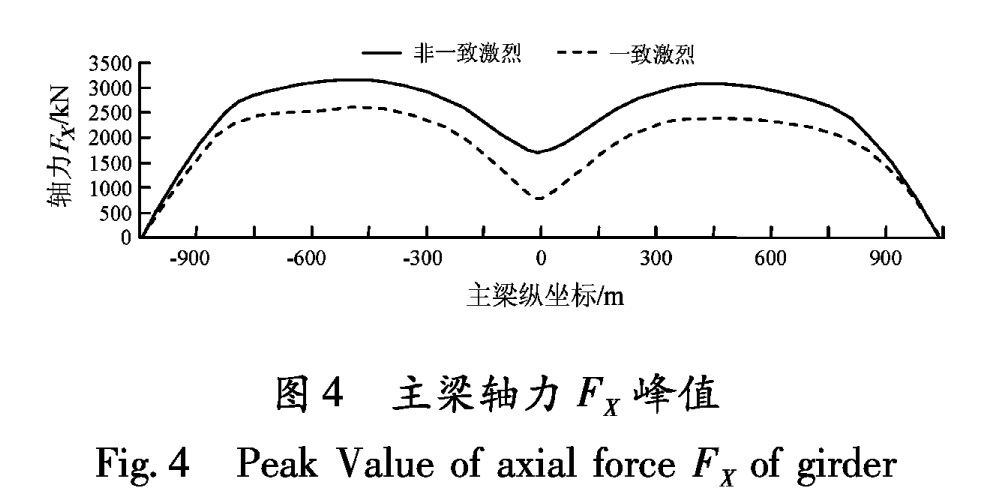
与一致激励相比,考虑局部场地效应后,北塔输入的功率谱比南塔要强。北塔边跨主梁的纵向弯矩增大10%,南塔中跨减小了24%左右,总体影响程度不是很显著,但对主梁轴力的影响非常显著。北塔塔梁交接处,轴力峰值增大22%,而跨中部位从770 kN增大到1 736 kN,增大约125%,但较大轴力主要集中在塔梁附近处,虽然跨中部位增大的相对值较大,但绝对值为1 000 kN左右,不会危及主梁的强度和刚度,同时,对主梁竖向剪力的影响甚微。
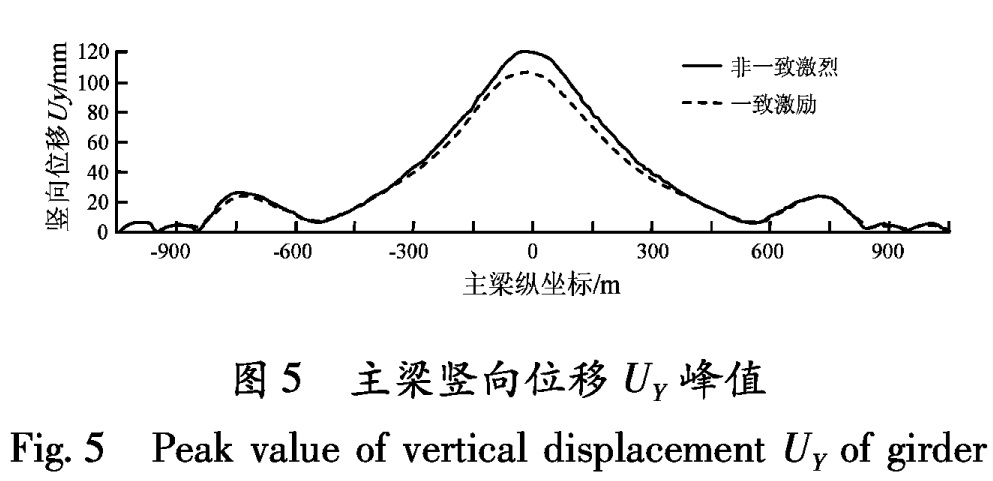
苏通大桥主跨为1 088 m,结构刚度较柔,局部场地效应对边跨主梁竖向位移几乎没有什么显著影响,但中跨主梁各部位竖向位移均为增大,其中跨中增大了14%左右(图3)。
图3 主梁纵向弯矩MZ峰值
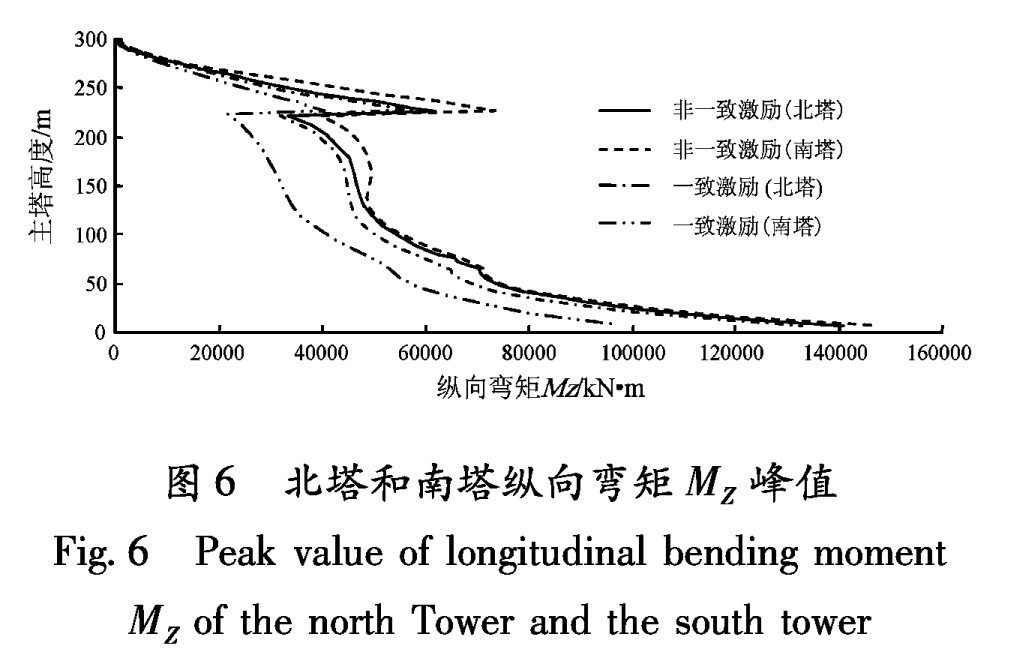
Fig.3 Peak value of longitudinal bending moment MZ of girder苏通大桥北塔和南塔的基础刚度有所差异,计算分析中考虑局部场地效应时,与一致激励相比,主塔结构的纵向弯矩和纵向位移变化显著,如图6和图7所示。这说明,多点激励下两岸主塔响应受本岸地震动激励的作用较大,而由对岸传来的地震动激励作用则相对较弱。主要原因是:① 苏通大桥主跨1 088 m,结构体系柔度很大,结构动力性能与结构自振特性关系密切(表2),且构件之间距离较远会导致二者之间的相互约束作用减小; ② 苏通大桥的主塔、过渡墩、辅助墩、主梁之间的约束关系,如辅助墩和过渡墩与主梁在纵向互不约束(表1),因而边界条件会影响结构响应。图4 主梁轴力FX峰值
Fig.4 Peak Value of axial force FX of girder图5 主梁竖向位移UY峰值
Fig.5 Peak value of vertical displacement UY of girder图6 北塔和南塔纵向弯矩MZ峰值
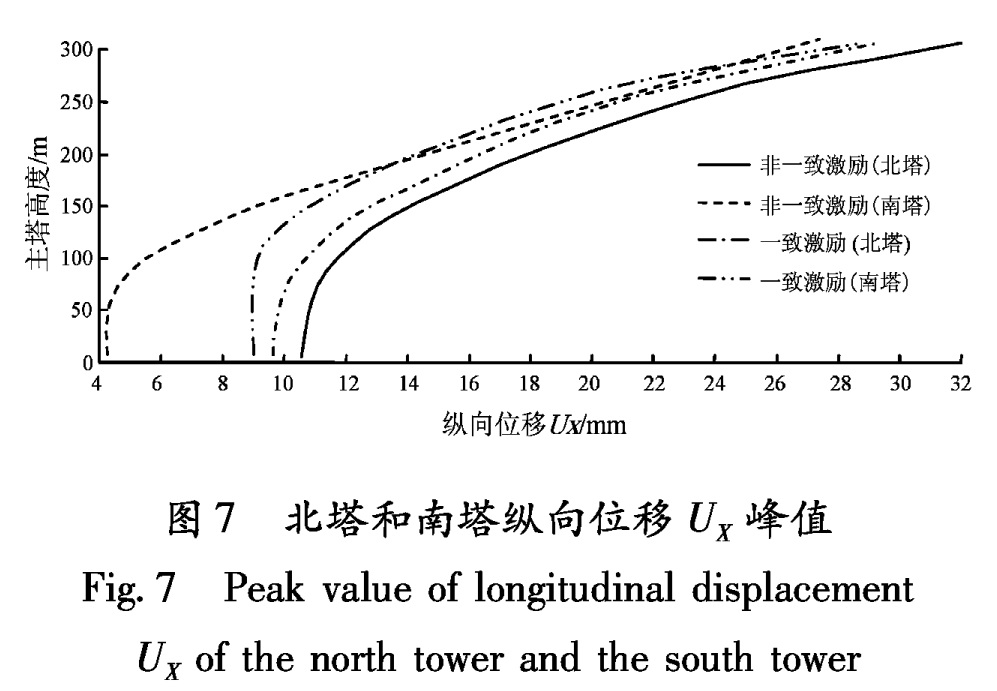
Fig.6 Peak value of longitudinal bending moment MZ of the north Tower and the south tower图7 北塔和南塔纵向位移UX峰值
Fig.7 Peak value of longitudinal displacement UX of the north tower and the south tower5 结论
(1)结构的动力特性是其抗震性能的基础,苏通大桥斜拉桥存在很强的三维运动耦合性,任何1个方向的地震动都可以引起结构3个方向的运动。
(2)与一致激励相比较,在考虑地震动的局部场地效应时,结构的动力响应在某些位置可能增大,也可能降低,说明地震动的局部场地效应对结构反应的影响与结构的特性、位置、边界条件等有关。
(3)局部场地条件对大跨度斜拉桥地震响应的影响很大,因此对于场地条件不同且跨径较大的斜拉桥结构,应根据实际场地条件进行非一致激励地震响应分析。
- 杜修力.1998.水工建筑物抗震可靠度设计和分析用的随机地震输入模型[J].地震工程与工程振动,18(4):76-81.
- 杜修力,陈厚群.1994.地震动随机模拟及其参数确定方法[J].地震工程与工程振动,14(4):1-5.
- 黄用军,王群.1997.二维地震动的局部场地效应的研究[J].武汉工业大学学报,19(2):52-54.
- 解丽,卢勇坤,非明伦. 2008. 汶川8.0级地震桥梁震害[J].地震研究, 31(增刊):530-534.
- 林家浩,张亚辉,赵岩.2001.大跨度结构抗震分析方法及近期进展[J].力学进展,31(3):250-360.
- 屈铁军,王君杰,王前信.1996.空间变化的地震动功率谱的实用模型[J].地震学报,18(1),55-62.
- 王光远,程耿东,邵卓民,等.1999.抗震结构的最优设防烈度与可靠度[M].北京:科学出版社.
- 周勇军,全伟,贺拴海. 2006. 基于正交试验的连续刚构桥地震响应敏感性参数分析[J]. 地震研究, 29(2):176-182.
- Zerva A.1988.Lifeline response to spartially variable ground motion[J].Earthquake Engineering and Structural Dynamics,17(7):361-379.
- Zerva A.1991.Effect of spartial variablity and propagation of seismic ground motion on the response of multiply supported structures[J].Probabilistic Engineering Mechanics,(7):217-226.