基金项目:国家自然科学基金项目“重大水利水电工程地震动参数研究”(50679084)、科技部“十一五”科技支撑计划项目“高坝深层抗滑稳定性评估技术”第六专题名称“地震作用下高坝深层动力抗滑稳定分析与抗震措施研究”(2008BAB29B03)、第四十三批博士后科学基金资助项目“多点多维非平稳地震加速度时程合成方法研究”(20080430447)共同资助.
(1.南昌航空大学 土木建筑学院,南昌 330063; 2.中国水利水电科学研究院 抗震中心,北京 100044; 3.中国水利水电科学研究院 综合事业部,北京 100044)
(1.College of Civil Engineering,Nanchang Hangkong University,Nanchang 330063,Jiangxi,China)(2.Earthquake Engineering and Technology Research,China Institute of Water Resourcesand Hydropower Research,Beijing 100044,China)(3.Department of Integrated Service
evolutionary power spectra; multi-filter technique; spatial variability; stochastic prediction model
备注
基金项目:国家自然科学基金项目“重大水利水电工程地震动参数研究”(50679084)、科技部“十一五”科技支撑计划项目“高坝深层抗滑稳定性评估技术”第六专题名称“地震作用下高坝深层动力抗滑稳定分析与抗震措施研究”(2008BAB29B03)、第四十三批博士后科学基金资助项目“多点多维非平稳地震加速度时程合成方法研究”(20080430447)共同资助.
基于我国台湾地区SMART-1密集台阵强震记录资料和Kameda的时变功率谱模型,利用多重滤波技术和非线性最小二乘法拟合得到每条记录的Kameda模型参数值; 通过分析模型参数随频率变化的散点图分布规律,建立了时变功率谱模型参数随频率变化的随机模型。采用随机振动理论和多元统计分析方法,分析了沿波传播方向距离、垂直于波传播方向距离及测点所在位置土层厚度等局部空间位置变化对时变功率谱模型参数的影响规律,探讨了时变功率谱模型参数的空间分布形式,建立了各模型参数随空间坐标变化的随机预测模型,从而为重大工程多点输入地震动参数的确定和多点输入加速度时程的合成提供实用模型。
Based on the strong-motion datasets of SMART-1 array and Kameda's evolutionary power spectral model,the evolutionary power spectral of earthquake ground motions were calculated by using multi-filter technique.Each parameter of the Kameda's evolutionary power spectral model were fitted by nonlinear least squares fit.Stochastic model of each parameter varying with frequency were constructed by analyzing the distribution law of spot figures of parameters varying with frequency.The spatial variability stochastic prediction models were studied by analyzing the influence of the variation of planar coordinate and soil thickness.Results gained in this paper can be applied to non-stationary,multi-point ground motion simulation.
引言
地震波在传播过程中存在行波效应、相干效应、衰减效应及局部场地效应等,使得地震动存在明显的空间变化性。即使在50 m范围内,地震动特性也存在明显的差异,表现在时空的复杂变化形式和分布上(Feng,Hu,1982)。地震动的时空变化性很早就引起了人们的注意(Bogdanoff et al,1965)。Housner(1957)对建筑物基础的运动及其附近地震动的观测都表明,是否考虑地震动的空间变化将导致结构基础响应的较大差异(廖松涛,2001)。地震动的时空变化性也已被我国新丰江大坝强震台网记录、我国台湾地区SMART-1密集台阵记录和美国巴柯依玛拱坝强震台网的实测记录等所证实(陈厚群,1997)。大量的计算分析表明,地震动的空间变化性对平面尺寸较大的结构物,如核电站、大坝、桥梁、地下管线等的地震反应具有明显影响,忽略地震动的空间变化性会给地震反应计算结果带来较大的误差(廖松涛,2001)。大跨度结构必须考虑地震动参数空间变化性的影响。
国内外不少学者在地震动空间变化性方面做了富有成效的工作,提出了不少相关(相干)函数模型,如Hao模型(Hao,1991)、Harichandran-Wang模型(Harichandran,Wang,1986,1990)、Harichandran模型(Harichandran et al,1996)、冯启民模型(冯启民,胡聿贤,1981)等等,但他们的研究主要限于时域地震动相关性(或频域相干性)等问题上,就局部场地地震动参数的空间变化性问题展开的研究较少。Okawa et al(2001)、Deng et al(1989)、胡进军(2003)分析了地震动参数沿深度的变化情况,陈厚群等(1995)分析了坝址基岩河谷地震动不均匀分布等问题,屈铁军(1995)分析了水平地震分量随波传播方向距离及测点所在位置土层厚度的变化规律,但他们的研究仅限于考虑水平地震分量的幅值和平稳功率谱等参数沿波传播方向距离和深度变化的影响,而垂直于波传播方向距离的影响及竖向地震动分量的空间变化性未加以考虑。
目前工程界普遍认为,无论就地震动特征的全面描述还是就抗震设计的合理要求而言,地震动工程参数必须同时反映幅值、频谱和持时三方面的影响,仅考虑地震动的幅值和频谱特性是不够的(易立新等,2004; 杨杰英等,2007)。时频谱不仅考虑了地震动的幅值和频谱特性,还将地震动的持续时间包含在内,能较为全面地反应地震动的特性(钟菊芳,2006; 钟菊芳,胡晓,2009)。本文以我国台湾地区SMART-1密集台阵的强震记录资料为数据基础,采用统计分析的方法,探讨局部场地上时变功率谱模型参数随波传播方向距离、垂直于波传播方向距离和土层厚度的变化而产生的空间变化规律。
1 强震记录资料的选取
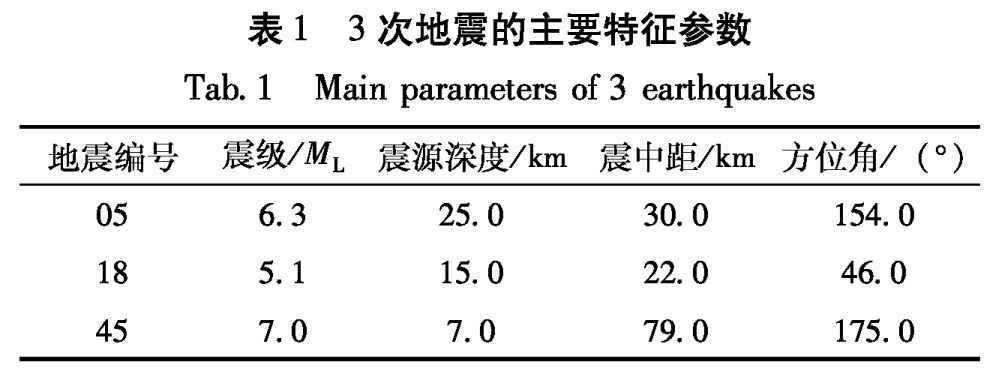
SMART-1台阵是二维差动台阵,设置有39个测点,中心设C-00测点,在3个半径分别为200 m、1 000 m、2 000 m的同心圆周上各布设12个测点,编号由内往外依次为I-01~I-12、M-01~M-12、O-01~O-12,共36个测点; E-01和E-02则位于距离C-00南端2.8 km和4.8 km处。E-02布置在裸露的基岩上,其余38个均设在土层地表上。由于E-01和E-02距离C-00测点较远,本研究中不使用,只使用其余37个测点的记录资料。笔者选用SMART-1台阵记录到的震中距大于20 km的3次地震资料,其主要特征见表1,其中震中距指震源到C-00测点的距离。
地震编号 震级/ML 震源深度/km 震中距/km 方位角/(°)05 6.3 25.0 30.0 154.018 5.1 15.0 22.0 46.045 7.0 7.0 79.0 175.02 地震记录时变功率谱的计算及模型参数的确定
2.1 计算频率点的确定工程界通常对0.1~10 Hz频率范围内的地震动较为感兴趣,Berrill和Hanks(1974)对胶片记录的长周期误差进行分析后认为记录资料的低频截止频率取FL=0.125 Hz较为合理。据此,本文对0.13~10.03 Hz频率范围内的频率点进行分析。为了使计算结果具有代表性又不至于工作量过大,计算时取频率间隔Δf=0.18 Hz,共计56个频率点。
2.2 地震记录时变功率谱的计算地震记录的时变功率谱采用Kameda(1975)的多重滤波方法计算得到,即通过计算加速度记录时程输入下单质点体系在不同频率点的反应值来实现滤波的作用。基底输入加速度时程为x(t)时单质点体系的运动方程为
y¨(t)+2βω0y·(t)+ω20y(t)=-x(t). (1)
式中,y(t)、y·(t)、y¨(t)分别为相对位移、相对速度和加速度反应,β为阻尼系数,ω0为圆频率。
根据位移传递函数定义有
E[y2(t,ω0)]=∫∞∫-∞〖JB<1*|〗H(ω)〖JB>1*|〗2Sx(t,ω)dω.(2)
式中,Sx(t,ω)为输入x(t)的时变功率谱,H(ω)为振子的传递函数。
如果时变功率谱Sx(t,ω)比传递函数〖JB<1*|〗H(ω)〖JB>1*|〗2平滑,则可近似得到
Gx(t,ω)=(2βω0)/(π)E[y2(t,ω0)+(y·2(t,ω0))/(ω20)].(3)
式中,Gx(t,ω)=2Sx(t,ω0)为单侧功率谱。
在计算时,首先令β=5%,按单自由度线性反应分析方法计算各频率点的加速度反应时程,然后积分得到速度和位移反应时程,再依(3)式计算得到各频率点的时变功率谱值Gx(t,ω)。由于计算结果随时间变化的波动很大,这里选用Parzen窗函数(大崎顺彦,1980)对计算得到的时变功率谱进行平滑
G'(t,ω)=∫∞∫-∞G(t,ω)W(ω-Ω)dΩ.(4)
式中,G'(t,ω)和G(t,ω)分别为平滑前后的时变功率谱; Parzen窗函数W(ω)=3/4u(sin(uω)/4〖JB<1*/〗(uω)/4)4,u=280/151/b,为控制谱窗带宽的参数,可依据谱窗等效带宽b值定,文中取b=π(rad/s)(大崎顺彦,1980)。
2.3 时变功率谱模型的选取及参数值的确定Kameda(1975)通过对强震记录资料的分析,建立了如下时变功率谱模型:
Gx(t,2πf)=a2m(f)〖JB<2|〗(t-ts(f))/(tp(f))〖JB>2|〗2exp〖JB<2*|〗2〖JB<2|〗1-(t-ts(f))/(tp(f))〖JB>2|〗〖JB>2*|〗, t>ts.(5)
式中,ts(f)为起始时间,通常取G(t,2πf)=0.1Gmax(t,2πf)对应的t值; ts(f)+tp(f)为时变功率谱峰值对应的时间; am(f)为时变功率谱峰值的平方根。
该模型能较好地反映时变功率谱随时间和频率的变化规律,所以笔者直接采用该模型进行计算。利用非线性最小二乘法回归拟合方法拟合3次地震各个测点记录对应的56个频率点的ts(f)、am(f)和tp(f)参数值,部分拟合结果见图1。
3 时变功率谱模型参数的空间变化性分析
3.1 时变功率谱模型参数的影响因素分析时变功率谱模型参数ts(f)、am(f)和tp(f)不仅是频率的函数,还随震级和距离的变化而变化。对于同一次地震来说,SMART-1密集台阵内各个测点记录均来自同一震源,具有相同的震级,震级对不同测点参数值的影响可忽略; 震中距相对于各个测点相对位置的差异来说要大得多,这里也忽略各个测点间震中距的差异对模型参数的影响,只考虑频率变化对参数的影响。从时变功率谱模型参数随频率变化的散点分布图来看,模型参数随频率的变化规律可用下式来描述:
{t's(f)=ts(f)-tm=α1+β1log10 f+γ1(log10 f)2
log10am(f)=α2+β2log10 f+γ2(log10 f)2
log10tp(f)=α3+β3log10 f.(6)
式中,αi、βi、γj(i=1,2,3; j=1,2)为回归系数; f为频率; tm为同一测点所有频率点对应ts的平均值。
通过对SMART-1台阵3次地震的不同测点记录资料的拟合分析,可得到不同地震对应于各个测点记录的α1、β1、γ1、α2、β2、γ2、α3、β3。
3.2 空间变化性随机方程的建立计算中用到的37个测点均布设在半径为2 km范围内的同一地表土层上,台阵的平面尺寸与震中距相比要小得多,且对于同一次地震,各测点记录具有相同的震源机理、相同的震级和震源深度,这里忽略震源机制及传播路径对同一次地震各测点时变功率谱的影响,仅考虑测点所在局部场地条件对时变功率谱模型参数α1、β1、γ1(i=1,2,3; j=1,2)的影响。本文以沿波传播方向距离为x轴,垂直于波传播方向距离为y轴,最靠近震源的测点在坐标轴上的投影为坐标原点。各测点除x和y向坐标不同外,从地质剖面图上看,各测点所在地的土层厚度(从基岩到地表土层的深度)也有较大的差异,最薄处为170 m,最厚处为610 m,设各测点所在地的土层厚度为h。
为了探讨空间位置的变化对时变功率谱模型参数的影响程度,笔者采用以下随机模型
ΔY=aΔx+bΔy+cΔhm+ε.(7)
式中,ΔY为空间位置坐标的变化引起的模型参数的变化量; Δx、Δy、Δh分别为沿波传播方向距离、垂直于波传播方向距离及土层厚度的变化量; 幂指数m分别取1、1.5和2; a、b、c为拟合系数; ε为无穷小量。当系数b=c=0时为模型(1); a=c=0时为模型(2); a=b=0且m=1时为模型(3); c=0时为模型(4); b=0且m分别取1、1.5、2时分别为模型(5)~(7); a=0、m分别取1、1.5、2时分别为模型(8)~(10); a、b、c均不为零且m分别取1、1.5、2时分别为模型(11)~(13)。
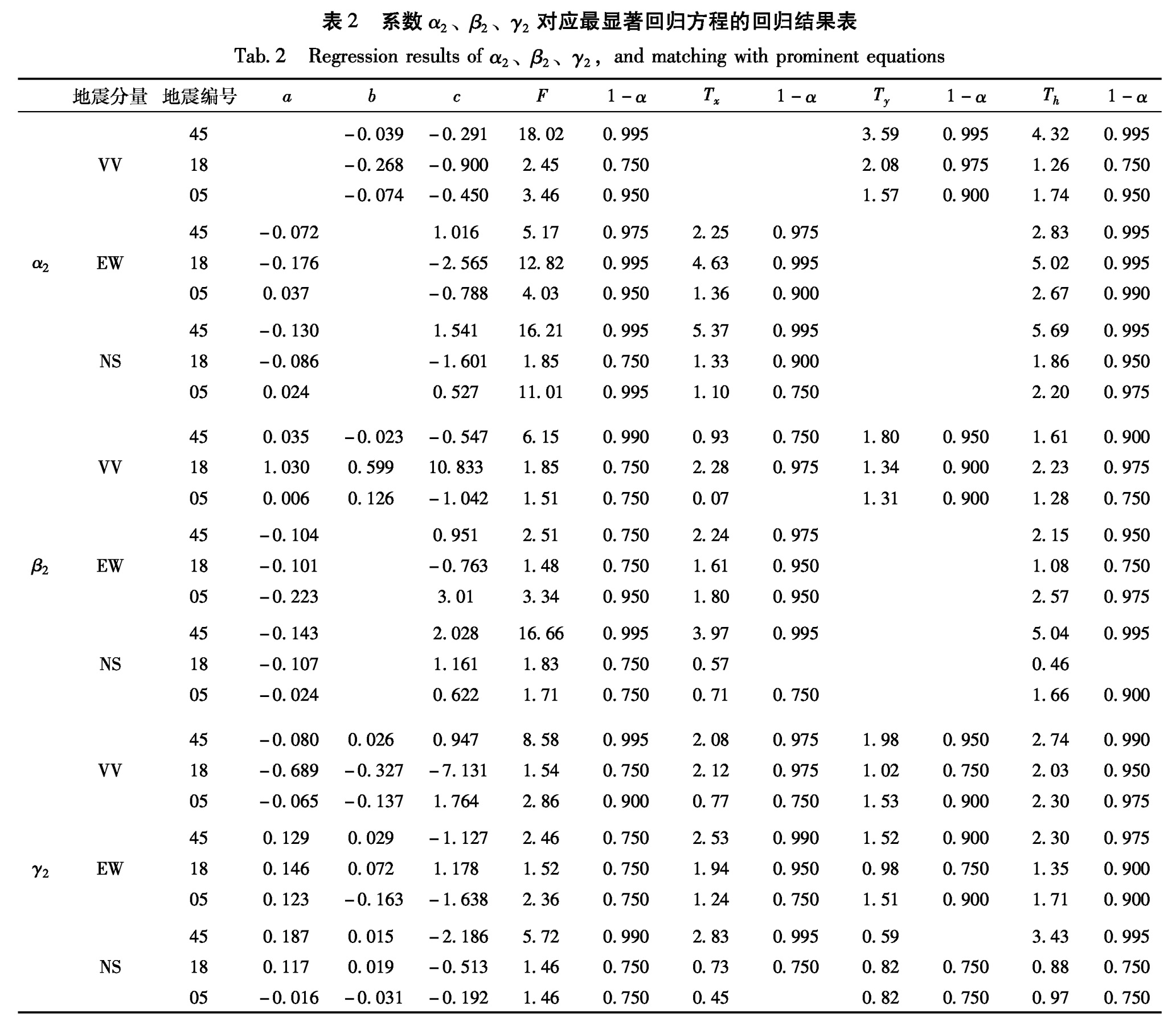
3.3 回归方程的显著性检验方法回归方程的显著性采用F检验法(朱勇华等,1999)进行检验,回归方程中各个自变量对因变量的影响程度的大小则采用偏回归平方和比较法中的T值法(朱勇华等,1999)来检验。对于相同的测点数、自由度数来说,F值越大,置信水平1-α也就越大,回归方程的显著性就越强,方程的拟合效果也就越好。Tj值越大,对应的1-α值就越大,xj对因变量y的影响程度也就越高。这里取13组回归方程中F和Ti的置信水平最高的方程为最显著回归方程。表2列出了系数α2、β2、γ2对应最显著回归方程的回归结果。
3.4 回归结果与分析从回归结果来看,α1及β3的回归结果显著性的一致性不强。相比较来说,13组方程中方程ΔY=aΔx+cΔh+ε的显著程度较好,取该方程为α1和β3的最显著方程,即两系数主要受x和h变化的影响,受y变化的影响不大。竖向分量β1在方程ΔY=bΔy+c(Δh)2+ε中的回归结果最为显著。水平分量β1对应13组回归方程的显著性都不强,一致性较差,x、y及h的变化对它的影响不明显,为了满足多点输入的需求,以ΔY=aΔx+bΔy+cΔh+ε作为它的最显著回归方程。竖向分量γ1回归结果的显著性强于两水平分量,其中竖向分量γ1在方程ΔY=aΔx+bΔy+c(Δh)2+ε中的F值和T值的置信水平都较高。经比较,以方程ΔY=aΔx+bΔy+c(Δh)2+ε作为竖向和水平分量γ1的最显著方程。
无论是竖向分量还是两水平分量,系数α2回归结果显著性的一致性都很强,最显著回归方程的F、Ti值置信水平均在75%以上,竖向分量和水平分量的最显著回归方程分别为ΔY=aΔx+cΔh+ε和ΔY=aΔx+c(Δh)2+ε。竖向分量β1将随x、y及h的变化而变化,水平分量β1将随x及h的变化而变化,分别以方程ΔY=aΔx+bΔy+cΔh+ε和ΔY=aΔx+c(Δh)2+ε作为竖向分量和水平分量的最显著回归方程。系数γ2将随x、y及h的变化而变化,但h的变化对竖向分量和水平分量γ的影响程度不同,竖向分量γ2与h呈线性变化,水平分量γ2则随h的1.5次方变化,竖向分量和水平分量的最显著回归方程分别为ΔY=aΔx+bΔy+cΔh+ε和ΔY=aΔx+bΔy+c(Δh)1.5+ε。
表2 系数α2、β2、γ2对应最显著回归方程的回归结果表
Tab.2 Regression results of α2、β2、γ2,and matching with prominent equations竖向分量α3主要受y变化的影响,x及h的变化对系数α3的影响不大,以方程ΔY=bΔy+ε为最显著回归方程。水平分量α3则主要受x及h变化的影响,选方程ΔY=aΔx+c(Δh)2+ε作为最显著回归方程,对应方程的显著性水平也较高。
从回归系数的正负号来看,不同地震、不同分量对应回归系数的正负号也不完全相同,受随机因素的影响,表现为有正有负,但从总的趋势来看,α1随x增大和h的减小而增大; 竖向分量β1随y和h的增大而减小,水平分量β1随x的减小、y和h的增大而增大; 竖向分量γ1随x、y和h的增大而增大,水平分量γ1随x的减小、y和h的增大而增大。竖向分量α2随y和h的增加而减小,水平分量α2随x的减小和h的增大而增大; 竖向分量β2随x的减小和y与h的增加而减小,水平分量β2则随x的减小和h的增加而增大; 竖向系数γ2随x和y的增加、h的减小而减小,水平向系数γ2随x和h的增大、y的减小而增加。竖向分量α3随y的增加而增大,水平分量α3则随x的减小和h的增加而减小; 系数β3随x、h的增加而增大。
3.5 随机预测模型时变功率谱模型参数在空间上的分布规律可通过空间位置的变化对模型参数变化量的影响程度来反映。在多点输入中,当已知第i输入点的时变功率谱模型参数α1i、β1i、γ1i、α2i、β2i、γ2i、α3i、β3i值,以及第i和j输入点间的空间位置变化量Δx、Δy、Δh时,可根据空间位置变化对模型参数的最显著回归方程,计算得到第j输入点的时变谱模型参数α1j、β1j、γ1j、α2j、β2j、γ2j、α3j、β3j值。计算公式如下:
{α1j=α1i+a11Δx+c11Δh
β1j=β1i+{b12Δy+c12Δh2
a13Δx+b13Δy+c13Δh
α1j=γ1i+a14Δx+b14Δy+c14Δh2 竖向、水平(VV-EW-NS)分量
竖向(VV)分量
水平(EW-NS)分量
竖向、水平(VV-EW-NS)分量,(10)
{α2j=α2i+{b21Δy+c21Δh
a22Δx+c22Δh2
β2j=β2i+a23Δx+{b23Δy+c23Δh
c24Δh2
γ2j=γ2i+a25Δx+b25Δy+{c25Δh
c26Δh1.5竖向(VV)分量
水平(EW-NS)分量
竖向(VV)分量
水平(EW-NS)分量
竖向(VV)分量
水平(EW-NS)分量,(11)
{α3j=α3i+{b31Δy
a32Δx+c32Δh2
β3j=β3i+a33Δx+c33Δh竖向(VV)分量
水平(EW-NS)分量
竖向、水平(VV-EW-NS)分量.(12)
式中,aij、bij、cij为回归系数。
将α1j、β1j、γ1j、α2j、β2j、γ2j、α3j、β3j值代入式(6),得到第j输入点的t's(f)、am(f)、ap(f)值。将t's(f)、am(f)、ap(f)值代入到时变功率谱模型式(5),得到第j输入点的时变功率谱值。
4 结论
基于SMART-1台阵3次地震记录,通过分析台阵所在场地局部空间位置坐标的变化对地震动参数变化量的影响,我们系统地分析了沿波传播方向距离x、垂直于波传播方向距离y及测点所在位置土层厚度h的变化对时变功率谱模型参数的影响规律。从分析结果来看,空间位置坐标x、y、h的变化对不同地震分量的不同模型参数的影响规律及影响程度不相同,不同的模型参数在空间上的分布形式不一致。根据时变功率谱模型参数的空间变化随机预测模型及不同测点间的空间位置变化量可方便地进行时变功率谱模型参数的估计,为多点输入地震动参数的确定提供实用模型。
由于所统计的记录资料来自于SMART-1密集台阵,该台阵位于平坦冲积谷上,因此所得时变功率谱模型参数的空间随机预测模型仅适用于平坦的土层场地地震动参数的预测。对于基岩场地,特别是峡谷型坝基等场地,空间预测模型的适用性还有待于强震记录资料的验证。
- 陈厚群.1997.当前我国水工抗震中的主要问题和发展动态[J].振动工程学报,10(3):253-257.
- 陈厚群,侯顺载,张力飞,等.1995.拱坝多点输入动力反应的试验研究[J].水利学报,(8):12-20.
- 大崎顺彦.1980.地震动谱分析入门[M].吕敏申,谢礼力,译.北京:地震出版社.
- 冯启民,胡聿贤.1981.空间相关地面运动的数学模型[J].地震工程与工程振动,1(3):1-8.
- 胡进军.2003.地下地震动参数研究[D].哈尔滨:中国地震局工程力学研究所.
- 廖松涛.2001.工程场地地震动相干函数的数值分析[D].上海:同济大学.
- 屈铁军.1995.地面运动的空间变化特性研究及地下管线地震反应分析[D].哈尔滨:国家地震工程局力学研究所.
- 杨杰英,李永强,刘丽芳,等.2007.地震主要因素对地震伤亡人数的影响分析[J].地震研究,30(2):182-187.
- 易立新,胡晓,钟菊芳.2004.基于EPA的重大工程设计地震动确定[J].地震研究,27(3):271-276.
- 钟菊芳.2006.重大工程场地地震动输入参数研究[D].南京:河海大学.
- 钟菊芳,胡晓.2009.时变功率谱模型参数衰减规律研究[J].地震研究,32(2):73-79.
- 朱勇华,邰淑彩,孙韫玉.1999.应用数理统计[M].武汉:武汉水利电力大学出版社.
- Berrill J B,Hanks T C.1974.High frequency amplitude errors in digitalized strong-motion accelerations[J].EERL.Vol.Ⅳ.Paper Q.Report No.74-104.
- Bogdanoff J L,Goldber J L,Shiff J C.1965.The effect of ground trans-mission time on the response of long structures[J].BSSA.55(3):627-640.
- Feng Q M,Hu Y X.1982.Spatial Correlation of earthquake motion and Its effect on structural response[A],Proceedings of US-PRC,Bilateral Workshop on Earthquake Engineering[C].1:A-5-1-A-5-14.
- Harichandran R S,Wang W J.1986.Response of simple beam to spatially varying earthquake excitation[J].Journal of the Engineering Mechanics Division.American Society of Civil Engineering,114(9):1526-1540.
- Harichandran R S,Wang W J.1990.Response of multi-span beams to spatially incoherent seismic ground motions[J].Earthquake Engineering and Structural Dynamics,19:819-832.
- Harichandran R S,Hawwari A,Sweidan B N.1996.Response of long-span bridges to spatially varying ground motion[J].Journal of the Structural Engineering,122(5):476-484.
- Hao H.1991.Response of multiply supported rigid plate to spatially correlated seismic excitation[J].Earthquake Engineering and Structural Dynamics,20:821-838.
- Housner G W.1957.Dynamic pressure on accelerated fluid containers[J]. BSSA, 47(1):15-35.
- Kameda H.1975.Evolutionary spectra of seismogram by multi-filter[J].Journal of Engineering Mechanism Division,American Society of Civil Engineering,101:787-801.