基金项目:云南省重点项目“云南强震活动与板缘动力学机制研究(JCYB-20080601-4)”和中国地震局“小江断裂带的中长期地震潜势定量研究”项目(200708035)联合资助.
(Earthquake Administration of Yunnan Province,Kunming 650224,Yunnan,China)
time-to-failure method,accelerating energy release,location search,Xiaojiang Fault Zone
备注
基金项目:云南省重点项目“云南强震活动与板缘动力学机制研究(JCYB-20080601-4)”和中国地震局“小江断裂带的中长期地震潜势定量研究”项目(200708035)联合资助.
使用云南区域台网记录的地震目录资料,采用破裂时间法模拟前兆地震序列能量加速释放过程,系统研究了能量加速释放模型参数估计方法及强震位置搜索技术,详细推导了预测模型基本公式,对小江断裂带上发生的19次主震事件进行了模拟,结果表明:强震前能量加速现象是一种普遍现象,主震前,与主震相差2.5个震级单位的前兆序列出现能量加速释放所占的比例为80%; 由前兆序列模拟得到的预测时间和震级与实际值很接近,主震震级预测精度约为±0.5级,预测主震发生时间误差约为±0.5年; 搜索半径和搜索时间与主震震级成线性正相关关系; 采用主震位置搜索技术,对小江断裂带未来中期6~7级强震可能危险区进行了预测。
On the basis of earthquake catalog data recorded by Yunnan region network,using time-to-failure method,we simulated the process of Accelerating energy release of Precursory earthquake sequence.Systematic research of accelerating energy release of model parameter estimation method and strong earthquake location search technology.Derived the basic formula of prediction model.We simulated 19 times the main seismic events of Xiaojiang Fault Zone.The results show that the accelerating energy release before strong earthquakes is a universal phenomenon.Appears to accelerate the release of energy of precursor earthquake sequence of the difference between the main shock with 2.5 magnitude units as a proportion of 80%.Prediction time and magnitude which precursor sequence simulated with the actual value is very close to.The main earthquake magnitude prediction accuracy level of about ±0.5,time error of ±0.5 year.Search radius and the search time and the main earthquake magnitude is a linear positive correlation.Using the main shock location search technique to predict medium-term strong earthquake risk areas in Xiaojiang Fault Zone.
引言
强震前震源及附近地区地震活动会出现从平静至增强再到平静最后发震的过程,这一现象出现于绝大多数强震发生之前,是一种较为普遍的现象(钱晓东,刘祖荫,1999; 焦远碧,丁鉴海,2000)。地震活动处于平静时期时,地震平静持续时间往往相对较长,这一时期也称为能量积累时期,地震能量释放随时间呈现出平稳变化。当地震活动处于增强状态时,地震活动打破了之前的线性变化,单位时间内释放的能量远远高于平稳状态的能量,这一时期往往相对较短,如果我们用地震矩来衡量地震活动的强弱,则这一时期也称为加速矩释放AMR时期(Accelerating Moment Release),如果用能量来衡量就称为能量加速释放时期。这是一个非常重要的时期,因为它相对于长期地震活动平静而言,其状态发生了明显变化,这种状态的改变也是我们进行地震预测预报的根本依据。当地震活动处于能量加速释放以后,又会出现平静状态,平静时间往往非常短暂,随后发生强震。针对这种地震活动加速释放及与之相关联的其它表现形式,长期以来中外地震学家从不同方面作了大量研究,取得了较多研究成果。破裂时间理论(Theory of time-dependent rupture)就是近年来发展起来的对强震前普遍存在的能量加速释放过程具有较好描述的方法,这种方法近年来在国内外已取得了较大进展。
在国外,Bufe 和Varnes(1993)对美国旧金山地区1909年和1989年结束的两个地震活跃期的中强地震进行破裂时间法研究,较为准确地拟合出了强震发生的时间和震级; Sykes和Jaume(1990)利用美国旧金山地区地震序列资料,采用累积地震矩来识别加速的能量释放; Bowman等(1998)对1952~1994年期间美国加州圣安德烈斯断裂带上发生的M≥6.5地震事件,采用时间—破裂法模拟,取得了较好效果; Brehm 和 Braile(1998,1999)对新马德里地震带和南加州地区的20多次主震,用破裂时间法来识别前兆事件能量值加速曲线,模拟主地震前的能量加速释放过程,以此研究地震的中期预测,取得了较好结果。
在国内,蒋长胜等(2004)对1978年以来中国大陆109例5.7级以上强震进行AMR模拟,发现具有明显加速特征的有55例。杨文政等(1999,2000)对中国大陆华北、川滇和新疆地区的一些地震,采用非线性拟合的方法进行了地震活动加速拟合。王丽凤等(2004)模拟强震前应变释放加速现象,对中国和新西兰几次强震前加速情况进行了考察。秦嘉政和钱晓东(2004,2005)利用云南地区中小地震资料,采用改进型破裂时间法研究了云南地区中强地震前能量加速释放现象,即通过证实两个常数比例k/m是主震的函数,从而将破裂时间法方程的未知参数从4个减少到3个,改进了模拟方法,提高了预测精度。
从国内已有报道的研究成果来看,破裂时间法仍然是一个新领域,大多数研究仅仅是对强震前前兆事件的模拟,对未来强震危险性进行预测的深入研究不多,如利用地震活动加速释放来进行强震危险地点的搜索技术研究在国内仍未见报道。本文利用改进型破裂时间法,研究了云南小江断裂带中强地震前能量加速释放现象,应用强震危险地点搜索技术,对该区中长期强震危险地区进行了探索。
1 破裂时间方程
Das和Schools(1981)根据材料断裂力学理论,提出破裂时间理论,Varnes(1989)根据破裂时间方法理论,导出下式:
(dΩ)/(dt)=k/((tf-t)n).(1)
式中,k和n为常数,Ω为地震释放,它可以是地震大小的任何一种量度,如地震矩、地震能量等,t是某次地震的时间,tf为破裂时间或主震发生时间。当t=tf时,表示地震释放是无限的,代表临界点和预测的破裂时间。Bufe 和 Varnes(1993)以(1)式为基础,积分给出破裂时间方程:
∑Ω=K+k/m(tf-t)m.(2)
式中,∑Ω代表t时刻在选定区域内的累积地震释放,t为前兆事件的发震时刻。K为总的累积地震释放,tf为主事件发生时间,k,m为常数,其中m称为标度常数,与(1)式中常数n有关,m≠0,m=1-n,由观测资料确定。根据方程式(2)改写的地震能量破裂时间方程形式为
∑E1/2=(Kpe+Kms)+k/m(tf-t)m.(3)
式中,∑E1/2是t时刻在某一选定区域内地震释放的能量平方根的累积值,地震序列释放能量平方根的总累积值K由两部份组成(K=Kpe+Kms),其中Kpe代表前兆事件地震能量平方根的总累积值,Kms代表主震能量平方根,(3)式是一个含有4个未知系数的方程。如果采用能量平方根累积值作为地震释放的量度,为了减少每个网络点的计算量,Brehm和Brailie(1999)通过确定一个经验关系式f(Kms),来确定(3)式的系数k/m,以此减少方程的未知常数,由此,提出了改进型破裂时间方程,把式(3)改写为如下形式:
∑E1/2=(Kpe+Kms)-f(Kms)(tf-t)m.(4)
式中,f(Kms)为与主震矩相关确定的系数k/m值的函数。
秦嘉政和钱晓东(2004)利用云南地区60多次主震和美国新马德里地震带和南加州地区的20多次主震,得到
lg(k/m)=0.47lgM0-1.5.(5)
图1是数据拟合结果,图中实心圆表示云南地区地震,空心圆表示美国新马德里地震带和南加州地区地震。利用Kanamori(1977)给出的地震波能量和地震矩之间的线性转换关系图1 主震地震矩M0与系数k/m的关系
Fig.1 The relationship between the main earthquake seismic moment M0 and the coefficient k/mM0=2×104E.(6)
将地震矩转换成地震波能量E,结合方程式(5)可得到
f(Kms)=k/m=100.47lgM0-1.5.(7)
式中,Kms代表主震能量平方根,f(Kms)表示系数k/m与主震地震矩相关的函数,利用(6)、(7)式,就可以将(3)、(4)式中的4个未知系数(k,m,tf,Kms)减少为3个(m,tf,Kms)。
2 破裂时间法在小江断裂带中的主震模拟
3 主震位置搜索
3.1 NSR值上述对主震的预测,我们是假定主震的位置是已知的,而事实上人们并不知道主震的位置。将整个研究区域划分为n个网格,对于每一个网格线相交点,利用一系列不同的搜索半径R挑选地震前兆事件,构建每一个加速序列,确定它们的最小(Rmin)和最大(Rmax)搜索半径值,定义
NSR=(Rmax-Rmin)/(Rmin).(12)
NSR称为归一化搜索半径。确定能量加速序列Rmin和Rmax的方法为:
计算由给定的搜索半径建造的前兆序列标准差SC,同时计算采用直线方程拟合同一前兆序列的标准差SL,当SC <SL时,表明由搜索半径建造的前兆序列有加速释放过程,计算误差比C:
C=(SL)/(SC).(13)
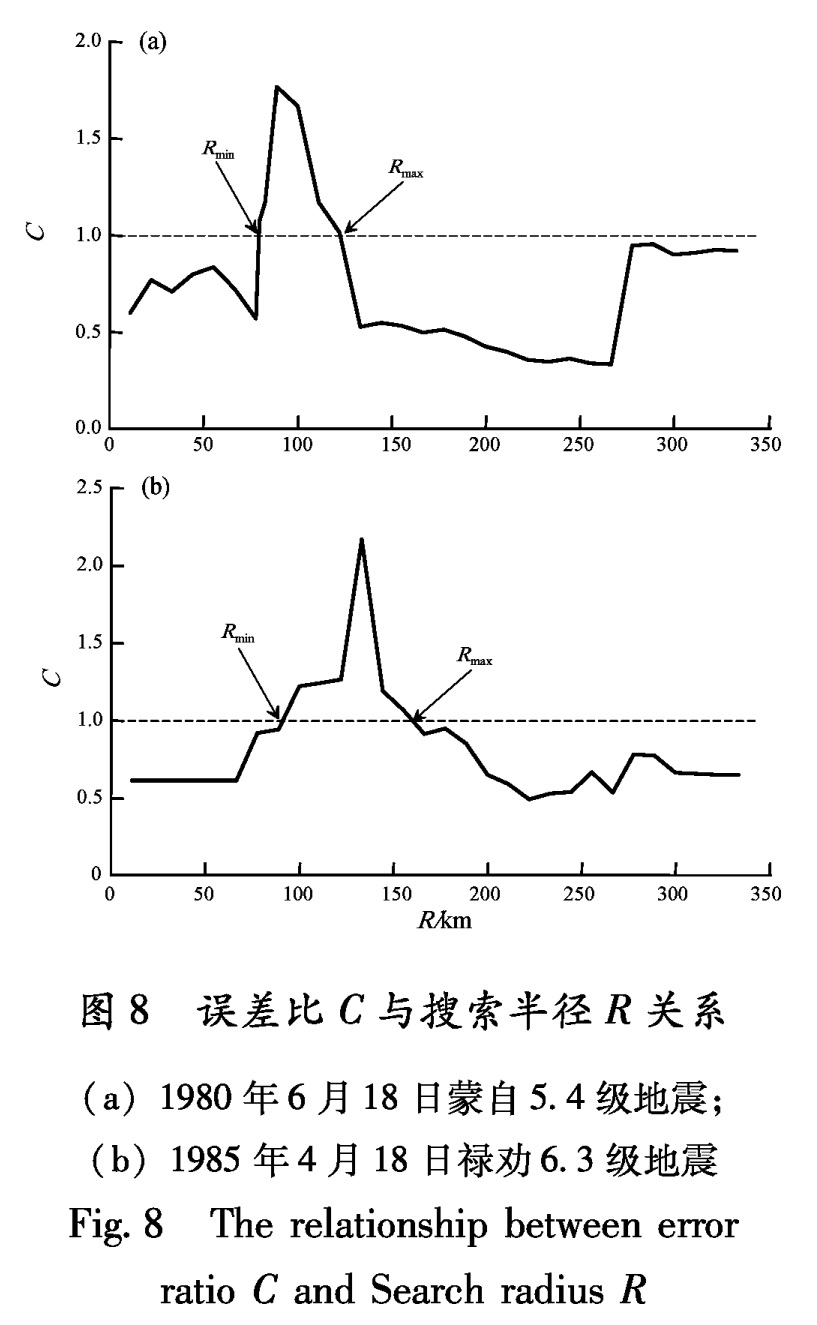
当C>1.0时,表示能量释放曲线非线性过程明显,当C≤1.0时,表示能量释放为线性(直线)增长过程,误差比C越大,前兆序列表现的加速过程越明显,定义C值大于1.0的一列搜索半径中最小的一个为最小搜索半径Rmin,最大的一个为最大搜索半径Rmax。
图8给出二次地震误差比与搜索半径R的关系曲线。以图8a为例来看,从搜索半径R=10 km开始搜索,以10 km为步长增加搜索区域,当搜索半径R增加到80 km时,误差比C值上升到1,R增加到90 km时,出现最大误差比Cmax,以后随着R的增加C值逐渐变小,从图中很容易确定Rmin、Rmax。
3.2 小江断裂带未来危险区估计对于小江断裂带(23.5°~28.5°N,102°~104°E),以0.5°为单位将该区划分为4×10=40个小网格,以每一个小方格中点为圆心,取一系列不同搜索半径,根据(4)式求出最大归一化的搜索半径NSR,最终可得到40个NSR值,根据小方格中心坐标可得到NSR等值线图。在计算能量加速曲线时,我们假设主震破裂时间为2009年以后3年,即2012年,主震震级分别为6级和7级,这样,在目前不知道主震发生的时间、震级和位置时,我们就可以根据现有的资料对未来一定时间(3年)发生一定强度的地震(6级或7级)危险地点进行估计。
图9为小江断裂带NSR等值线图。从未来3年该区发生6级地震危险地区来看(图9a),高NSR值地区主要是小江断裂带南端的通海一带地区,小江断裂带北端巧家和四川西昌之间,也出现高NSR值。从发生7级地震危险地区来看(图9b),高NSR值地区主要集中在小江断裂带北端的昭通与巧家一带,南端的通海附近也出现小片异常区域。总体上看,小江断裂带发生6级以上强震的危险地区为断裂带两端,断裂带中部发震的可能性小。4 讨论和结论
在强震发生之前,震源区中小地震活动会出现加速现象,这是人们在长期地震预测预报实践中观测到的强震前的普遍现象。余怀忠等(2004)通过岩石破裂声发射实验,发现岩石材料在受压破坏之前弹性能会出现明显的加速释放过程。强震前能量加速现象已成为人们普遍关注的现象,也是人们进行地震中长期预测的重要依据和手段,破裂时间法是研究这种现象的重要方法,但它还具有一定局限性,即它只对震前有能量加速释放的地震有效,对能量均匀释放或减速释放的地震则无能为力,而强震前未出现加速的地震比例近20%,蒋长胜(2004)也发现震前中小地震出现减速的现象,对这些地震的研究是今后的重要课题。破裂时间法的引入为我们提供了一种具有明确物理意义的预测预报方法,使用该方法近年来在云南地区进行了一些成功强震中短期预测(钱晓东,秦嘉政,2006),也说明该方法具有广阔的前景。
使用地点搜索技术时应该注意到,NSR越大,能量加速曲线越明显,NSR区域越大,能量加速系列曲线越多,最大的NSR即确定了即将发生主震的位置,考虑NSR高值是强震危险区时还需要注意以下三个问题,一是要排除干扰事件; 二是检查NSR是否稳定,即使用低于主震不同档次震级的前兆事件时NSR是否稳定; 三是NSR异常区是否存在能量亏缺,需要作长期能量估计显示一个地区显著存在能量亏缺。NSR未出现异常的地区并不意味着不存在发生主震的危险性,应当每隔一段时间(如1月、半年等)重新计算预测震级和时间,可能会出现新的NSR异常区,一直到加速系列发生主震或不再满足限定条件为止。
本文使用云南区域台网记录的地震目录资料,采用破裂时间法模拟前兆地震序列能量加速释放,系统研究了能量加速释放模型参数估计方法及强震位置搜索技术,详细推导了预测模型基本公式,对小江断裂带19次主震事件进行了模拟,结果表明:强震前能量加速现象是一种普遍现象,主震前,与主震相差2.5个震级单位的前兆序列出现能量加速释放所占的比例为80%; 由前兆序列模拟得到的预测时间和震级与实际值很接近,主震震级预测精度约为±0.5级,预测主震发生时间误差约为±0.5年; 搜索半径和搜索时间与主震震级成线性正相关关系; 采用主震位置搜索技术,对小江断裂带未来中期6~7级强震可能危险区进行了预测。
参考文献:
蒋长胜,吴忠良,史勇军.2004.中强震前地震活动矩释放加速现象(AMR)的普遍性问题[J].中国地震,20(2):119-125.
焦远碧,丁鉴海.2000.中等地震活动增强作为强震标志的研究[J].地震,20(2):15-19.
钱晓东,刘祖荫.1999.森下空间播散指数及其在地震预报中的应用[J].地震研究,22(4):357-364.
钱晓东,秦嘉政.2006.环境应力参数在2004年云南双柏5.0地震短期预报中的应用[J].中国地震,22(2):161-171.
秦嘉政,钱晓东.2004.利用前兆事件对云南地区地震进行中短期预测[J].地震学报,26(2):140-150.
秦嘉政,钱晓东.2005.云南会泽、文山两次M5.3级地震[J].地震研究.28(4):403-407.
王丽凤,马丽,David Vere-Jones,等.2004.随机AMR模型的参数估计及其在几次强震中的应用[J].地震学报,26(2):162-173.
杨文政,David Vere-Jones,马丽,等.2000.一个关于临界地震的临界区域判别的方法[J].地震,20(4):28-38.
杨文政,马丽.1999.地震活动加速模型及其在中国的应用[J].地震学报,21(1):32-41.
余怀忠,尹祥础,夏蒙棼,等.2004.地震临界点理论的实验研究[J].地震学报,26(增刊):122-130.
中国地震局.1998.地震序列的类型判别和震后趋势估计[A]//地震现场工作大纲和技术指南[M].北京:地震出版社:25-26.
Bowman D D,G Ouillon C G.Sammis,et al
本文使用云南区域台网记录的地震目录资料,采用破裂时间法模拟前兆地震序列能量加速释放,系统研究了能量加速释放模型参数估计方法及强震位置搜索技术,详细推导了预测模型基本公式,对小江断裂带19次主震事件进行了模拟,结果表明:强震前能量加速现象是一种普遍现象,主震前,与主震相差2.5个震级单位的前兆序列出现能量加速释放所占的比例为80%; 由前兆序列模拟得到的预测时间和震级与实际值很接近,主震震级预测精度约为±0.5级,预测主震发生时间误差约为±0.5年; 搜索半径和搜索时间与主震震级成线性正相关关系; 采用主震位置搜索技术,对小江断裂带未来中期6~7级强震可能危险区进行了预测。
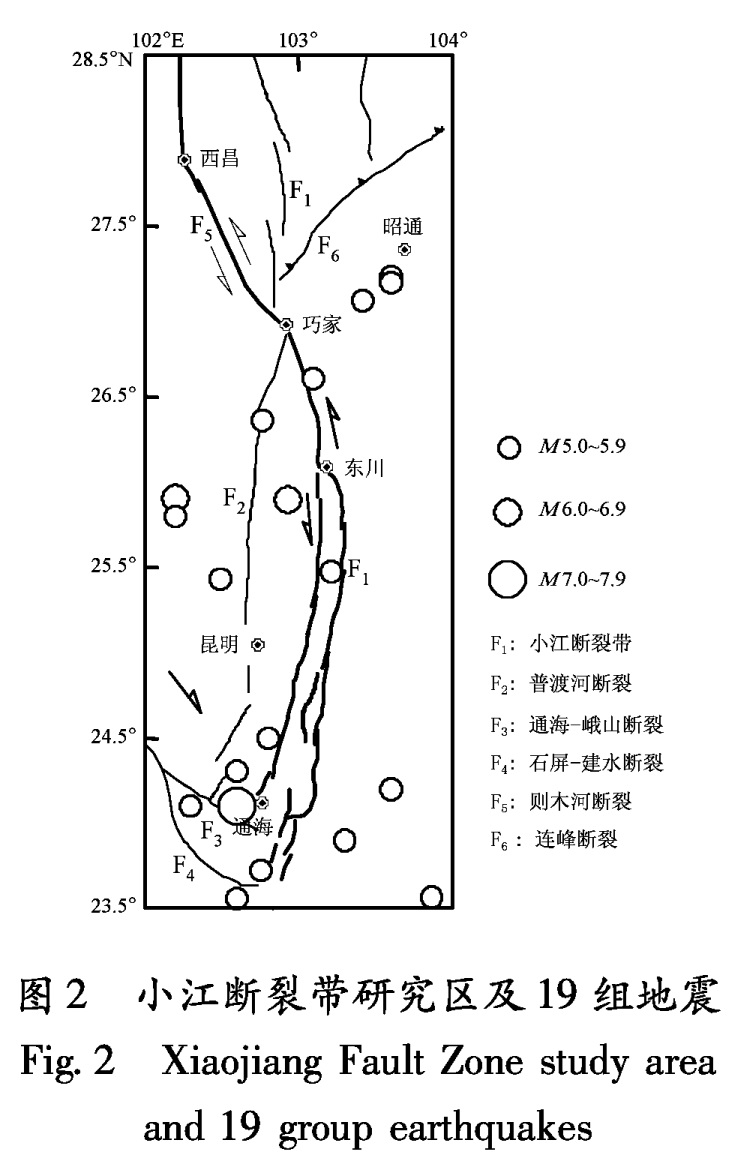
2.1 资料小江断裂带及周边地区(23.5°~28.5° N,102°~104° E)是一块长约560 km,宽约200 km的矩形区域(图2)。小江断裂带是云南地区较为重要的活动断裂带,位于康滇菱形地块南半部的东边界,呈SN走向,现代活动方式主要以左旋走滑为主。小江断裂带在东川以南分成东、西两支,相距约20 km,东支和西支左旋平均位移速率为6 mm/a。北部与四川则木河断裂相连,南部被红河断裂所截,与近NW向的石屏—建水断裂和通海峨山断裂相交,小江断裂带地区是一个地质构造较为复杂的区域。断裂带上的地震以频度低、强
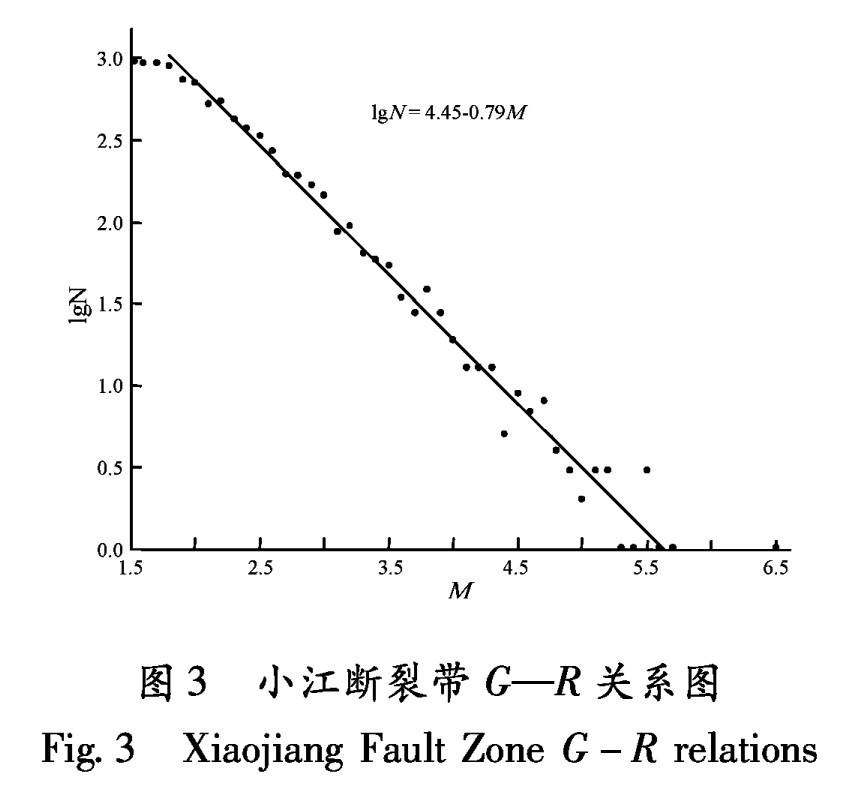
度高著称,如云南省最强烈的地震—1833年嵩明8.0级大地震就发生在其上。小江断裂属现今仍在活动的断裂,是一条强烈破坏性地震频发的地震带,因此,研究该地震带及其邻近地震带潜在强震发生的危险性,是一个十分重要的课题。图3给出该区1985年来M≥1.5地震的G-R关系,可以看到2级以下地震出现拐头现象,说明云南地震观测台网对该区2级以下地震记录不完整,本文使用2.5级以上地震,记录是完整的。
2.2 限定条件使用破裂时间法对小江断裂带地震进行模拟,为保证结果的可靠性,应该事先明确挑选地震的限定条件和准则:
(1)要有足够的地震数目,我们规定小震次数要大于15次。
(2)不存在干扰事件。由于云南地区地震活动频繁,根据实际模拟结果,允许在加速序列中的最大前兆事件应小于主震0.6个震级单位,因此,我们把前兆干扰事件定义为与主震震级相差0.6级以内的地震,因为当出现前兆干扰事件这个限制约束时,前兆事件加速曲线被截断,则不能用加速释放曲线进行模拟。“干扰事件”选取的依据主要有二点,一是国外一些学者都将震级差0.6级作为是否是“干扰事件”的度量(Brehm,Braile,1999); 二是根据目前常用的对地震类型的定义,主余型、双震型和震群型地震,也是将震级差0.6级作为判别标准(地震现场工作大纲和技术指南,1998)。
(3)删除余震。余震会造成模拟结果的失真,要删除M≥5地震的余震。
2.3 模拟结果根据破裂时间模型(4)式,对主震的破裂时间和震级进行预测,分三步进行:
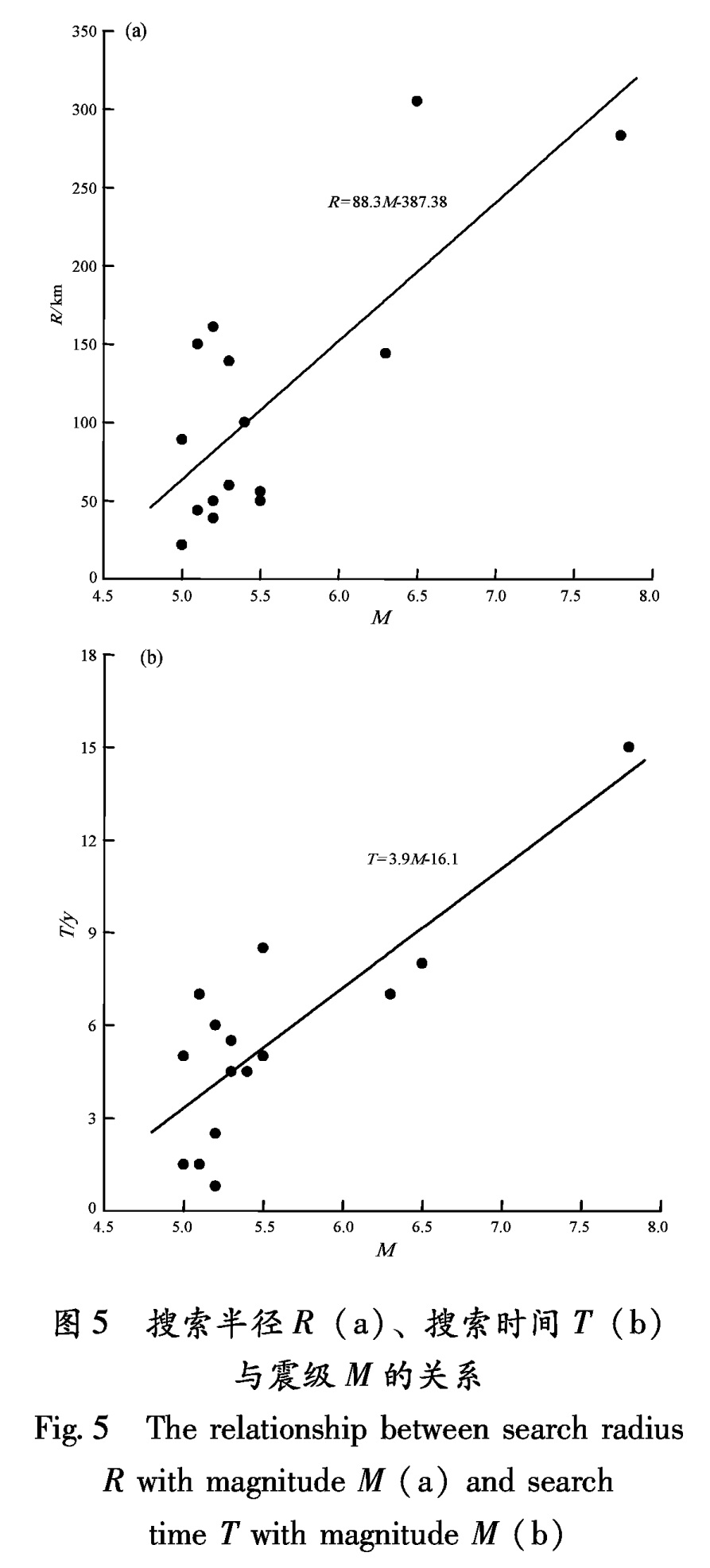
2.3.1 根据实际主震事件模拟利用主震的实际时间和震级,采用非线性最小二乘最优化程序,可估算出最优化k和m值,表1给出小江断裂带19次主震的模拟参数。当主震固定时,取震前一定时间期间范围(如0.5~30 a),以一定时间步长滑动计算(如0.5 a),对于每一个时间,取不同搜索半径进行拟合,可以得到相应标准差,最小值标准差对应的时间和半径为最终搜索时间和搜索半径。图4给出能量加速释放曲线结果。其中虚线为根据主震的实际时间和震级得到的最优化曲线。从表1中可以看出,19次地震中有4次不能得到能量加速释放曲线,约占20%。图5给出表1中搜索半径R和时间T与震级M的关系。从图中看到,搜索半径有随震级增大而增加的现象,利用最小二乘法直线拟合,近似存在关系
R=88.3M-374.4.(8)
由于数据太少,这种相关性不是太好(相关系数为0.6),但从图中可以看到,较大的主震,其前兆事件的影响区域也较大。同样,从图5b中看到,搜索时间与震级也存在线性增加关系,相关系数为0.7。
T=3.9M-16.1.(9)
2.3.2 构建标准差s误差图,预测主震震级和时间利用(4)式建立的预测模型对主震发生的时间和震级进行预测。以主震前的各个地震蠕变∑(Ei)1/2及发震时刻Ti为原始数据,不包括主震,震级范围取主震上下2个震级单位,一般在[4.5,7]区间,滑动步长取0.1级,时间范围取主震发生前0.5年至震后1年,步长为10天,以时间为横坐标,震级为纵坐标,构成一些网格和网格线,每个网格线的交点对应时间和震级,我们称之为预测时间tf和预测震级,对应的能量(蠕变)为Kms。根据(4)式,可得到无数条包含一个主震和所有前震的能量加速释放曲线,计算相应标准差
表1 用破裂时间法模拟小江断裂带19次主震及其基本参数
Tab.1 Simulation of 19 main shocks in Xiaojiang Fault Zone by time-to-failure method注:#表示无加速现象的前兆序列,不能被破裂时间法模拟.
s=((∑Ni=1(Yi-Y^i)2)/(N.))1/2.(10)
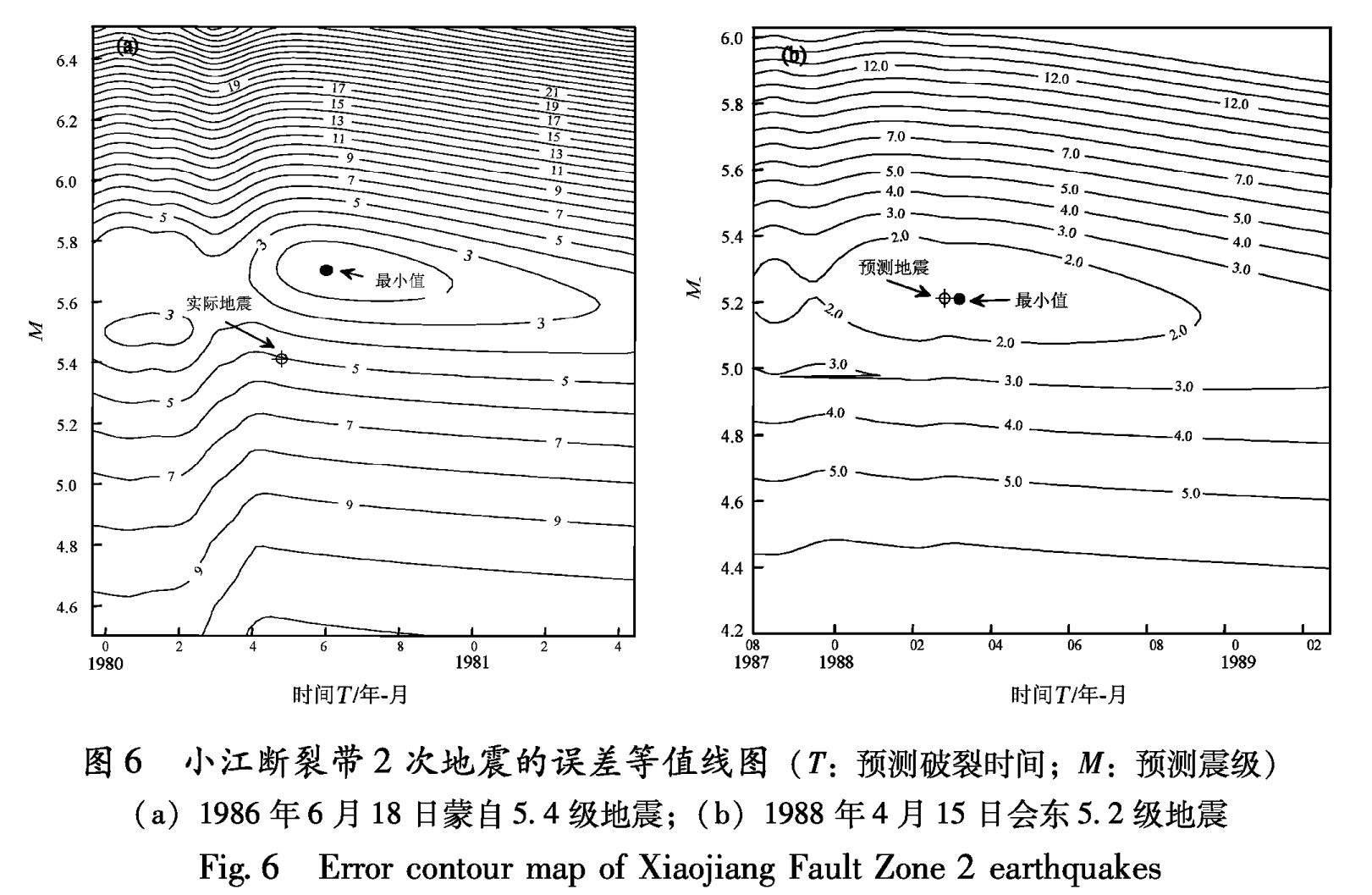
式中,Yi代表观测值,Y^i为理论值,N为数据次数,为便于比较,将s归一化到最大值为10,最小值为1。计算所有网格线交点并将结果赋予相应网格点,得到标准差s等值线图(图6)。
2.3.3 确定最佳预测震级和时间根据图6标准误差等值线图,找出最小值,其对应的震级和时间为误差最小的预测震级和时间,即最佳预测震级和时间,根据最佳预测震级和时间由(4)式拟合的预测曲线见图4中实线。
图4 小江断裂带2次地震的能量加速释放曲线(实线:根据实际主震模拟蠕变曲线; 虚线:最佳预测曲线)
(a)1986年6月18日蒙自5.4级地震;
(b)1988年4月15日会东5.2级地震
Fig.5 Curve of accelerating energy release of Xiaojiang Fault Zone 2 earthquakes2.4 预测检验通过(4)式建造加速序列时,使用最小震级分别低于主震2.5和3.0个震级单位,如果每个加速序列都满足给定的判据,每一个主震就至少有2个加速序列来模拟。表2给出小江断裂带19次主震事件用破裂时间法模拟的预测时间和预测震级结果,表中给出了两种加速序列的模拟结果,一种是低于主震2.5个震级单位的模拟预测结果,另一种是低于主震3.0个震级单位的模拟预测结果,可以看到有2次地震用低于主震3个震级单位不能被模拟。
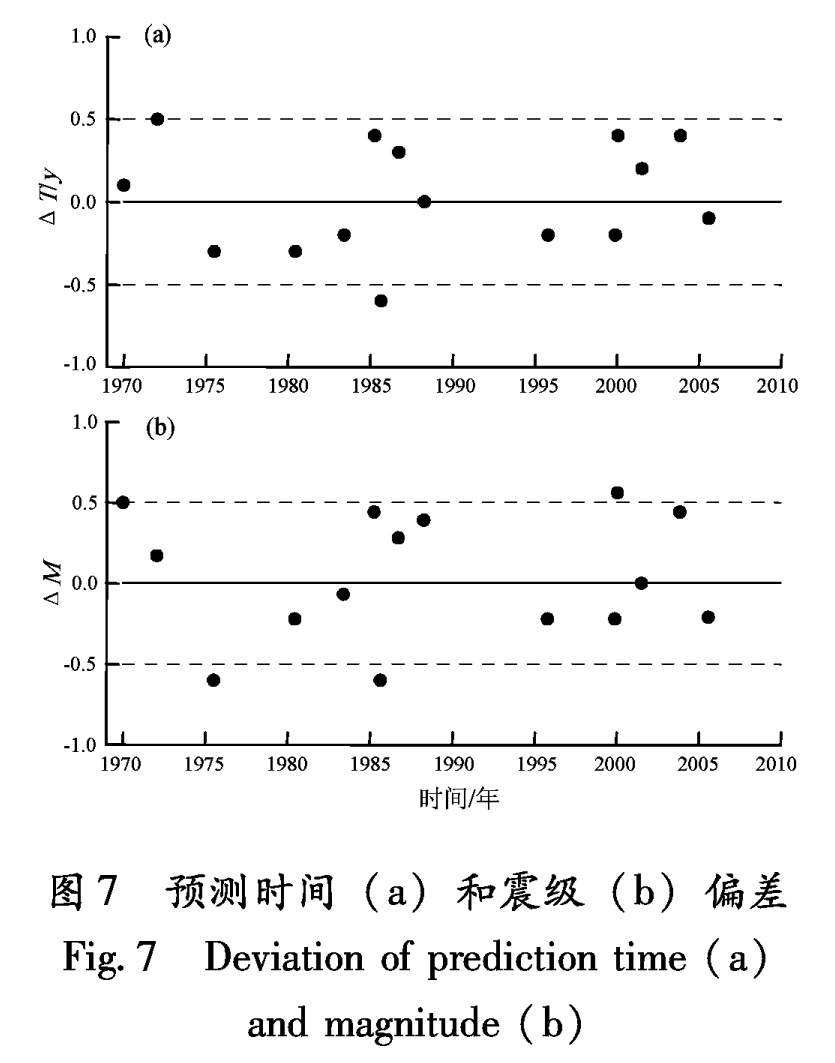
图7给出预测时间和预测震级偏差图,偏差值为实际值减预测值。对于时间预测(图7a),时间
图6 小江断裂带2次地震的误差等值线图(T:预测破裂时间; M:预测震级)
(a)1986年6月18日蒙自5.4级地震;(b)1988年4月15日会东5.2级地震
Fig.6 Error contour map of Xiaojiang Fault Zone 2 earthquakes偏差ΔT最小值为-0.6 a(即预测时间较实际时间推迟0.6 a),最大值为0.5年,平均值为0.33 a(取绝对值),图中两条虚线表示偏差为±0.5 a,可以看到只有一个点在两条虚线之外。可见这种方法对半年尺度的中期预测是有效的。
对于震级预测(图7b),震级偏差ΔM最小值为-0.6级(即预测震级比实际震级大0.6级),最大值为0.55级,平均值为0.28级(取绝对值),图中两条虚线表示偏差为±0.5级,绝大多数点在两条虚线之内,可见这种方法预测震级误差在0.5级以内,对于中期预测这样的误差在容许范围以内。
表2 小江断裂带19次主震破裂时间法模拟预测结果
Tab.2 Predictire parameters of 19 main shocks in Xiaojiang Fault Zone by time-to-failure method注:#表示无加速现象的前兆序列,不能被破裂时间法模拟; #1表示仅使用低于主震3.0个震级单位的前兆事件不能模拟主震事件.
- 蒋长胜,吴忠良,史勇军.2004.中强震前地震活动矩释放加速现象(AMR)的普遍性问题[J].中国地震,20(2):119-125.
- 焦远碧,丁鉴海.2000.中等地震活动增强作为强震标志的研究[J].地震,20(2):15-19.
- 钱晓东,刘祖荫.1999.森下空间播散指数及其在地震预报中的应用[J].地震研究,22(4):357-364.
- 钱晓东,秦嘉政.2006.环境应力参数在2004年云南双柏5.0地震短期预报中的应用[J].中国地震,22(2):161-171.
- 秦嘉政,钱晓东.2004.利用前兆事件对云南地区地震进行中短期预测[J].地震学报,26(2):140-150.
- 秦嘉政,钱晓东.2005.云南会泽、文山两次M5.3级地震[J].地震研究.28(4):403-407.
- 王丽凤,马丽,David Vere-Jones,等.2004.随机AMR模型的参数估计及其在几次强震中的应用[J].地震学报,26(2):162-173.
- 杨文政,David Vere-Jones,马丽,等.2000.一个关于临界地震的临界区域判别的方法[J].地震,20(4):28-38.
- 杨文政,马丽.1999.地震活动加速模型及其在中国的应用[J].地震学报,21(1):32-41.
- 余怀忠,尹祥础,夏蒙棼,等.2004.地震临界点理论的实验研究[J].地震学报,26(增刊):122-130.
- 中国地震局.1998.地震序列的类型判别和震后趋势估计[A]//地震现场工作大纲和技术指南[M].北京:地震出版社:25-26.
- Bowman D D,G Ouillon C G.Sammis,et al
- 本文使用云南区域台网记录的地震目录资料,采用破裂时间法模拟前兆地震序列能量加速释放,系统研究了能量加速释放模型参数估计方法及强震位置搜索技术,详细推导了预测模型基本公式,对小江断裂带19次主震事件进行了模拟,结果表明:强震前能量加速现象是一种普遍现象,主震前,与主震相差2.5个震级单位的前兆序列出现能量加速释放所占的比例为80%; 由前兆序列模拟得到的预测时间和震级与实际值很接近,主震震级预测精度约为±0.5级,预测主震发生时间误差约为±0.5年; 搜索半径和搜索时间与主震震级成线性正相关关系; 采用主震位置搜索技术,对小江断裂带未来中期6~7级强震可能危险区进行了预测。 参考文献:
- 蒋长胜,吴忠良,史勇军.2004.中强震前地震活动矩释放加速现象(AMR)的普遍性问题[J].中国地震,20(2):119-125.
- 焦远碧,丁鉴海.2000.中等地震活动增强作为强震标志的研究[J].地震,20(2):15-19.
- 钱晓东,刘祖荫.1999.森下空间播散指数及其在地震预报中的应用[J].地震研究,22(4):357-364.
- 钱晓东,秦嘉政.2006.环境应力参数在2004年云南双柏5.0地震短期预报中的应用[J].中国地震,22(2):161-171.
- 秦嘉政,钱晓东.2004.利用前兆事件对云南地区地震进行中短期预测[J].地震学报,26(2):140-150.
- 秦嘉政,钱晓东.2005.云南会泽、文山两次M5.3级地震[J].地震研究.28(4):403-407.
- 王丽凤,马丽,David Vere-Jones,等.2004.随机AMR模型的参数估计及其在几次强震中的应用[J].地震学报,26(2):162-173.
- 杨文政,David Vere-Jones,马丽,等.2000.一个关于临界地震的临界区域判别的方法[J].地震,20(4):28-38.
- 杨文政,马丽.1999.地震活动加速模型及其在中国的应用[J].地震学报,21(1):32-41.
- 余怀忠,尹祥础,夏蒙棼,等.2004.地震临界点理论的实验研究[J].地震学报,26(增刊):122-130.
- 中国地震局.1998.地震序列的类型判别和震后趋势估计[A]//地震现场工作大纲和技术指南[M].北京:地震出版社:25-26.
- Bowman D D,G Ouillon C G.Sammis,98.An observational test of the critical earthquake concept[J].J Geophys Rse,103:24395-24372.
- Brehm D J,Braile L W.1998.Application of the time-to-fsilure method for intermediate-term prediction in the New Madrid Seismic Zone[J].Bull Seism Soc Am,88:564-580.
- Brehm D J,Braile L W.1999.Intermediate-term earthquake prediction using the modified time-to failure in Southern California[J].Bull Seism Soc Am,89(1):275-293.
- Bufe C G,Varnes D J.1993.Predictive modeling of the seismic cycle of the Greater Francisco Bay Region[J].J Geophys Res,98(B6):9871-9883.
- Kanamori H.1977.The energy release in great earthquakes[J].J Geophys Res,82(2):981-2 978.
- Das S,Schools C H.1981.Theory of time-dependent rupture in the earth[J].J Geophys Res,86(B7):6039-6051.
- Sykes L R,Jaume S C.1990.Seismic activity on neighboring faults as a long-term precursor to large earthquakes in the San Francisco Bay area[J].Nature,348:595-599.
- Varnes D J.1989.Predicting earthquake by analyzing accelerating precursory seismic activity[J].Pure and Appl Geophys,130(4):661-686.