基金项目:云南省地震预报研究专项(JCYB-20080601-1)和中国地震局地震行业科研专项(200708038)联合资助.
(Earthquake Administration of Yunnan Province,Kunming 650224,Yunnan,China)
M≥6.0 strong earthquakes; interval distribution features; probability model; prediction-warning index; Yunnan region
备注
基金项目:云南省地震预报研究专项(JCYB-20080601-1)和中国地震局地震行业科研专项(200708038)联合资助.
系统分析了云南地区M≥6.0、M≥6.5和M≥7.0地震的间隔时间分布特征; 运用M≥5.0地震目录,基于G—R关系的年发生率和泊松分布模型,构建了云南地区M≥6.0、M≥6.5和M≥7.0地震的概率预测模型; 结合间隔时间分布统计特征和概率预测模型,对云南地区M≥6.0、M≥6.5和M≥7.0地震,建立了具有概率水平的三级预测预警指标:C(黄)、B(橙)、A(红)。
The interval distribution features of the earthquakes with M≥6.0,M≥6.5 and M≥7.0 occurred from 1900 to 2009 in Yunnan region are systematically analyzed in this paper.Based on the G-R relation and Poisson model,the probability model of the earthquakes with M≥6.0,M≥6.5 and M≥7.0 are built by using the M≥5.0 earthquake catalogs.Then,the three-grade,prediction-warning indexes(C(yellow),B(orange),A(red))for the earthquakes with M≥6.0,M≥6.5 and M≥7.0 are developed on the basis of the interval features and the probability model.
引言
地震重复(或间隔)时间(Recurrence Time)及其分布特征是地震活动性分析及地震危险性预测研究的一项主要内容。根据弹性回跳理论,一次大地震释放了地壳应变能,地壳应变在持续构造力的作用下重新积累,最终又形成另一次大地震。一般认为,一个区域、一个地震带上的地震(尤其是大地震)是按一定规律的时间间隔重复发生的。
基于某个震级限以上地震的间隔时间分布特征,选用概率密度函数(Probability Density Functions),构建一个地区或区域的地震概率预测模型,进行地震危险性的概率评估或预测,这种方法在国内外均有较多研究(Sun,Pan,1995; Matthews et al,2002; Field,2007; 易桂喜等,2002; 任俊杰,陈虹,2004; 张永庆等,2007)。在地震概率预测模型研究中比较常用的概率密度函数有泊松(指数)分布模型(Poisson or Exponential Model),对数正态分布模型(Log-normal Model),韦伯尔分布模型(Weibull Model),布朗流逝时间分布模型(Brownian Passage-Time Model),伽玛分布模型(Gamma Model)等,其中泊松(指数)分布模型在实际工作中应用最广泛(Kagan,Jackson,1999; Matthews et al,2002)。从1988年以来,美国加州地震概率研究组(Working Group on California Earthquake Probabilities,简称WGCEP)就一直在研究加州地区的地震概率预测模型,已先后发展了WGCEP-1988模型、WGCEP-1990模型、WGCEP-1995模型和WGCEP-2002模型(Field,2007),他们的研究工作比较有影响力和代表性。
从1996年2月3日丽江7.0级地震发生至2010年6月,云南地区7级以上地震平静已达14.41 a; 从2000年1月15日姚安6.5级地震发生至2010年6月,云南地区6.5级以上地震平静已10.46 a,该平静时间已超过1900年以来的历史极限。从统计上分析,经过这么长的平静时间,发生相应量级地震的危险性已很大,但它的危险性概率水平有多高?仅从统计上不能给出一个定量的危险性概率水平评估值。本文试图对这一问题进行研究。首先系统分析了云南地区M≥6.0、M≥6.5、M≥7.0地震的间隔时间分布特征,进而用M≥5.0地震目录,基于G—R关系的年发生率和泊松分布模型构建了云南地区M≥6.0、M≥6.5、M≥7.0地震的概率预测模型,并结合M≥6.0、M≥6.5、M≥7.0地震间隔时间统计特征,研究了具有概率水平的强震预测预警指标。
1 数据分析
本研究使用的地震目录是《中国历史强震目录》(公元前23世纪—公元1911年)(国家地震局震害防御司,1995)和《中国近代地震目录》(公元1912—1990年)(国家地震局震害防御司,1999); 1990~2009年的地震目录则使用中国地震台网中心测定的中国及邻区M≥5.0地震目录。从这些目录中选取1900~2009年云南地区(21°~29°N,97°~106°E)M≥5.0地震目录,并进行余震删除处理。余震删除的原则是参照C—S余震时间窗,作如下定义:6.0~6.9级地震,震后3个月内的余震被删除; 7.0~7.9级地震,震后6个月内的余震被删除。经余震删除处理后,1900~2009年云南地区M≥5.0地震共有324次,其中5.0~5.9级地震243次,6.0~6.9级地震68次,M≥7.0地震13次。相关研究认为,1929年以来云南地区M≥5.0 地震目录才基本完整(黄玮琼等,1994; 苏有锦等,2001)。20世纪早期云南地区地震漏记较严重,滇西南是主要的漏记地区,20世纪30年代以后该地区5级以上地震记录才较为完整(皇甫岗,李忠华,2010)。
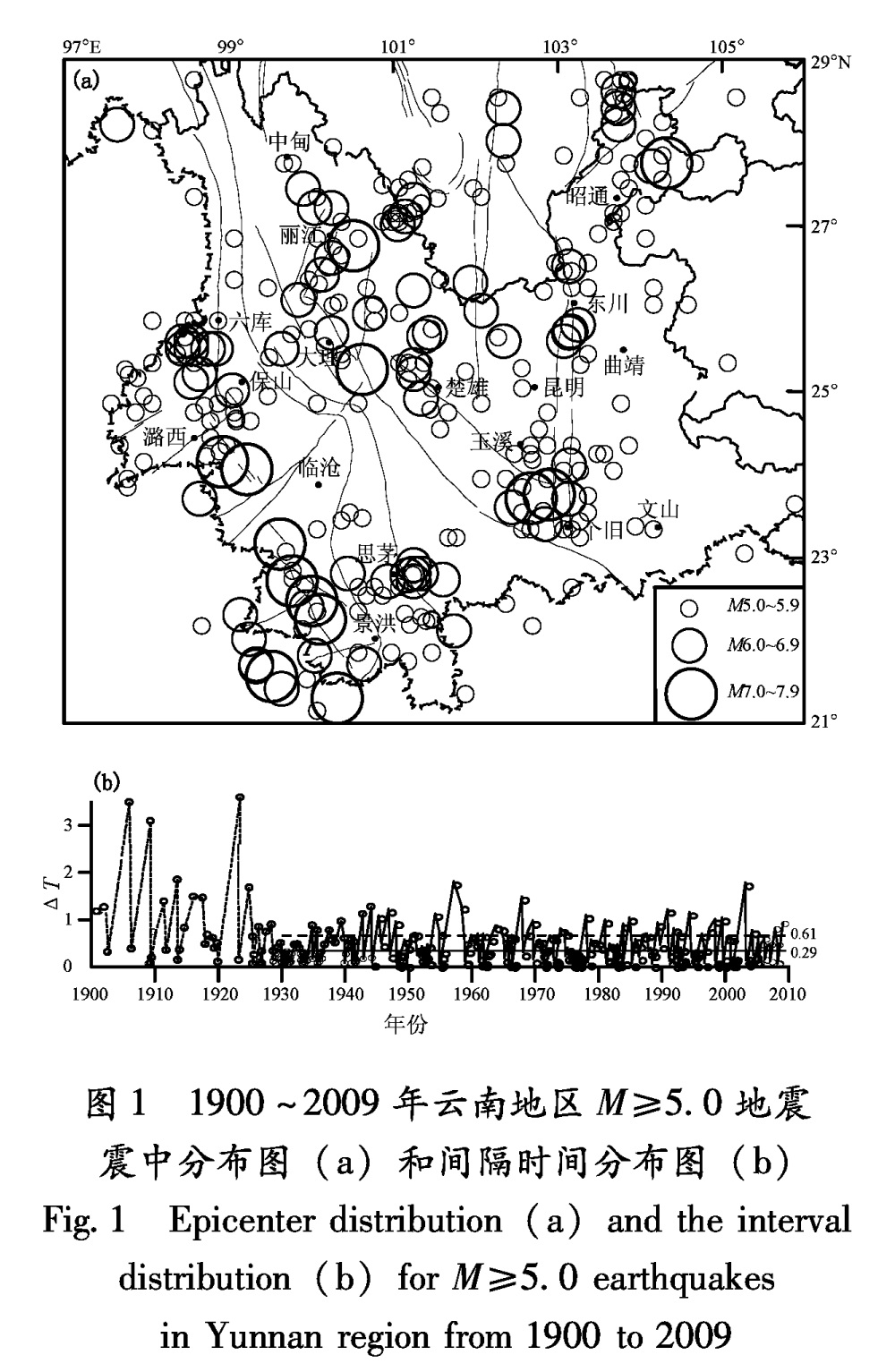
图1给出了1900~2009年云南地区M≥5.0地震的震中分布和间隔时间分布,在该研究区域内,实际上包括了四川省和中缅交界地区的部分地震。由图1b可见,大致在1930年前后,M≥5.0地震间隔时间分布有显著差别,1930年以后处于另一种分布状态,且较稳定。这进一步说明云南地区1930年以后的5级以上地震目录是基本完整的。
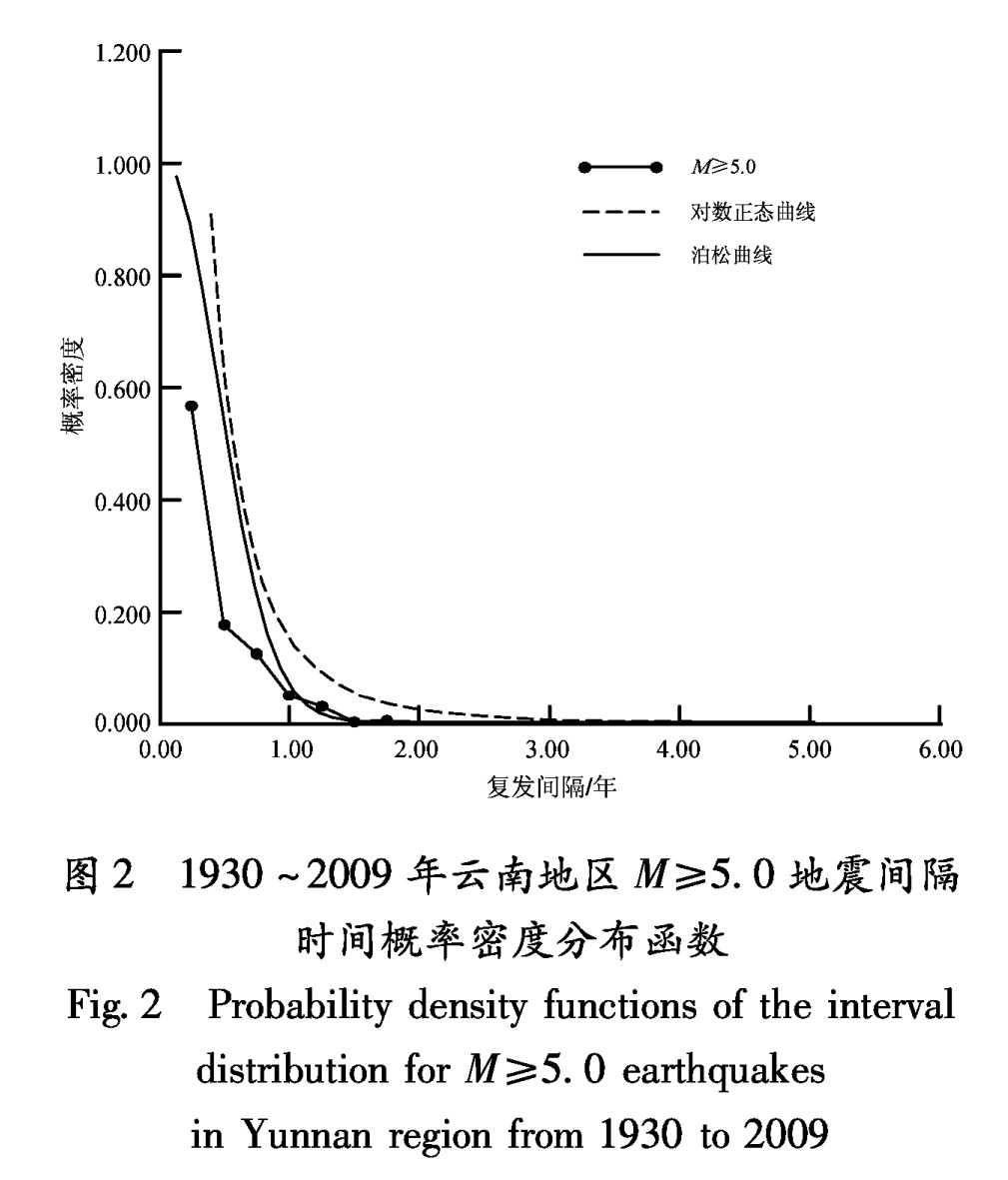
统计1930~2009年云南地区M≥5.0地震的间隔时间,共有277个样本,平均间隔时间为0.29 a,均方差为0.32 a,按0.25 a的步长进行统计。图2给出了间隔时间概率密度分布和用泊松(指数)分布模型和对数正态分布模型的拟合情况。泊松(指数)分布模型为f(t,u)=exp(-nμt)(Matthews et al,2002); 对数正态分布模型为f(t,y^-,σy)=1/((2π)1/2tσy)exp(-((lgt-y^-)2)/(2σy))(Zöller,Hainzl,2007),其中σy=(lg(1+σ/μ)2)1/2, y^-=lgμ-(σy2)/2。μ和σ是被拟合数据的平均值和标准差。1930~2009年云南地区M≥5.0地震间隔数据,平均值μ=0.29 a,均方差σ=0.32 a。
由图2可见,实际统计分布(点实线)与这两个模型均比较接近,泊松(指数)分布模型还更好一些。因此,对于云南地区M≥5.0地震间隔时间分布,本研究采用了泊松(指数)分布模型。
图1 1900~2009年云南地区M≥5.0地震震中分布图(a)和间隔时间分布图(b)
Fig.1 Epicenter distribution(a)and the interval distribution(b)for M≥5.0 earthquakes in Yunnan region from 1900 to 20092 M≥6.0、M≥6.5、M≥7.0地震间隔时间分布特征
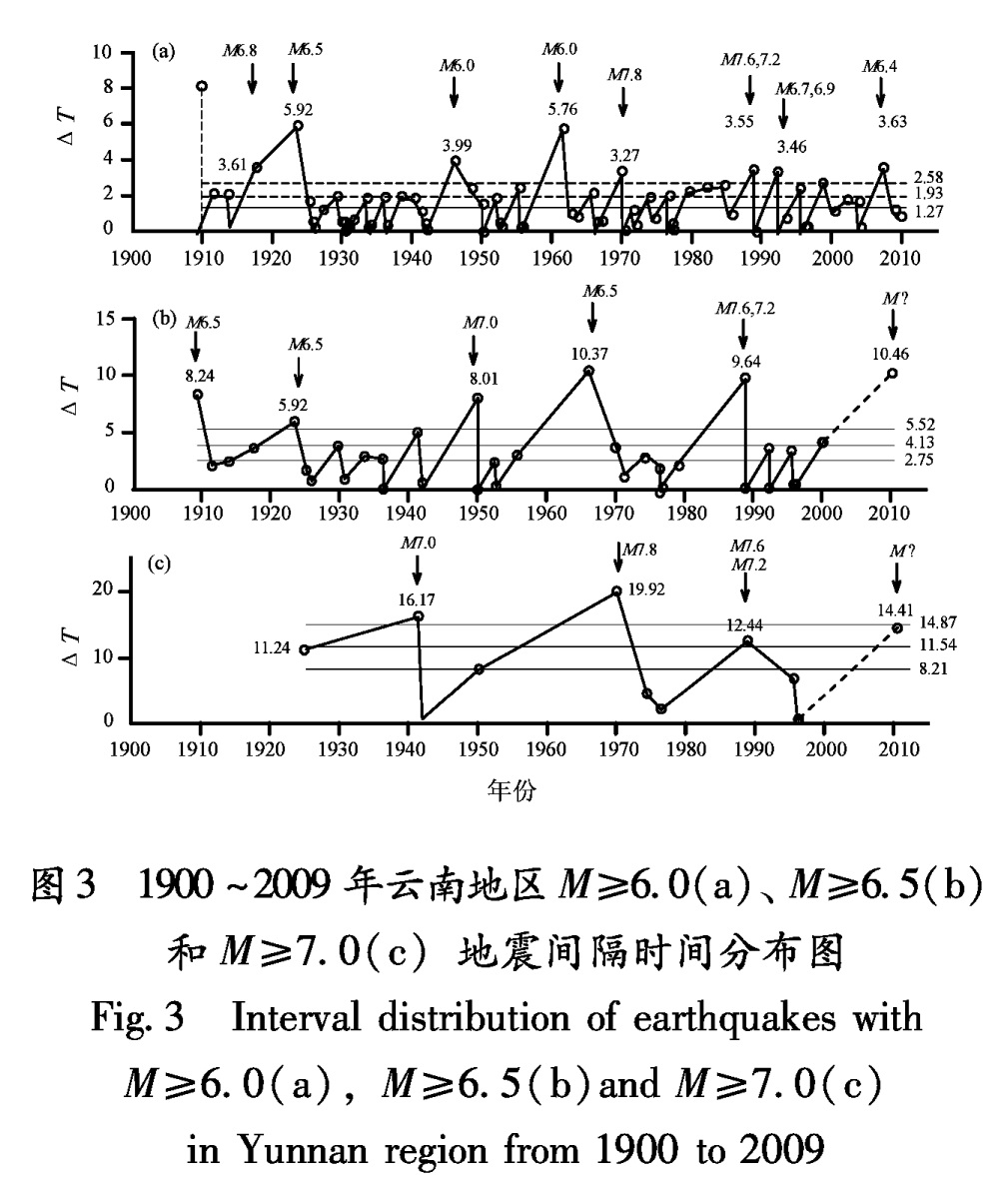
2.1 M≥6.0地震间隔时间分布特征图3a给出了1900~2009年云南地区M≥6.0强震的间隔时间分布。从1900年至1909年5月9年多的时间内,仅在1901年有过1次M≥6.0地震,其间出现了长达8年多的间隔。分析认为,云南地区M≥6.0地震目录资料,在1909年以前可能存在遗漏,1909年以后才基本完整。因此,本文仅对1909年以后的资料进行分析。1909~2009年云南地区共发生M≥6.0地震80次,有79个间隔时间样本,统计得到平均间隔时间为1.27 a,均方差σ为1.31 a; 0.5σ方差线为1.93 a,1σ方差线为2.58 a。统计表明,实际间隔时间大于平均间隔时间(1.27 a)的情况出现过30次,约占总样本数的38%,也就是说,约62%的M≥6.0地震的间隔时间在1.27 a内; 大于0.5σ方差线(1.93 a)的有21次,约占27%; 大于1σ方差线(2.58 a)的有9次,约占11%。
下面进一步分析间隔时间大于1σ方差线(2.58 a)的情况。由图3a可见,9次地震中有8次的间隔均在3 a以上,分别是3.61 a、5.92 a、3.99 a、5.76 a、3.27 a、3.55 a、3.46 a、3.63 a。从后续地震情况看,有5次直接对应了6.5级以上地震,其中2次为7级以上地震(1970年通海7.8级、1988年澜沧—耿马7.6、7.2级地震)。因此,若6级以上地震出现较长平静时间(3 a以上),就要特别警惕发生6.5级以上甚至7级以上地震的危险性。
2.2 M≥6.5地震间隔时间分布特征1900~2009年云南地区共发生M≥6.5地震37次,有36个间隔时间样本。M≥6.5地震的平均间隔时间为2.75 a,均方差为2.77 a; 0.5σ方差线为4.13 a,1σ方差线为5.52 a(图3b)。大于平均间隔时间(2.75 a)的情况出现过14次,约占总样本数的39%,即约61%的M≥6.5地震的间隔时间在2.75 a内; 大于0.5σ方差线(4.13 a)的有6次,约占17%; 大于1σ方差线(5.52 a)的有5次,约占14%。
间隔时间大于1σ方差线(5.52 a)的有5次,分别是8.24 a、5.92 a、8.01 a、10.37 a、9.64 a,其中有2次直接对应了7级以上地震(1950年勐海7.0级、1988年澜沧—耿马7.6、7.2级地震)。由图3b可见,从2000年1月15日姚安6.5级地震发生至2010年6月,云南地区6.5级以上地震平静已达10.46 a,为1900年以来最长的一次,这可能预示着发生6.5级以上地震或7级以上地震的危险性已经很大。
2.3 M≥7.0地震间隔时间分布特征1900~2009年云南地区共发生M≥7.0地震11次(组)(1976年龙陵7.3、7.4级双震和1988澜沧—耿马7.6、7.2级双震各计为1次(组)),有10个间隔时间样本。M≥7.0地震平均间隔时间为8.21 a,均方差为6.66 a; 0.5σ方差线为11.54 a,1σ方差线为14.87 a(图3c)。实际间隔时间大于平均间隔时间(8.21 a)的情况出现过4次,约占总样本数的36%; 大于0.5σ方差线(11.54 a)3次,约占27%; 大于1σ方差线(14.87 a)2次,约占18%。
1941年澜沧7.0级地震前,7级地震平静时间为16.17 a; 1970年通海7.8级地震前,7级地震平静时间为19.92 a; 1988澜沧—耿马7.6、7.2级地震前,平静时间为12.44 a。目前,云南地区7级以上地震平静时间已达14.41 a,已接近1σ方差线,这可能预示着发生7级以上地震的危险性已经很大。
3 泊松概率模型
3.1 地震年发生率和泊松概率若考虑存在震级上限Mmax,Dong等(1984)、Sun和Pan(1995)给出了基于G—R关系的地震年发生率
N(m)=(e-λm-e-λMmax)/(e-λMmin-e-λMmax)N(Mmin)
(Mmin≤m≤Mmax).(1)
λ由下式确定:
1/λ+(Mmine-λMmin-Mmaxe-λMmax)/(e-λMmin-e-λMmax)=M^-.(2)
式中Mmax为研究区最大的可能地震,Mmin是统计震级下限,M^-是统计样本的平均震级。
如果地震重复时间(间隔时间)分布符合泊松(指数)分布模型,则可由下式计算危险性概率(Sun,Pan,1995):
P(t)=1-etN(m).(3)
式中,P(t)为在未来t年发生震级大于等于m的概率; N(m)是震级大于等于m地震的年发生率,由(1)式计算。
对1930~2009年云南地区M≥5.0地震目录(即数据模型),取震级上、下限分别为Mmin=5.0,Mmax=8.0,统计计算得到N(Mmin)=3.475(即1930~2009年发生M≥5.0地震278次,T=80 a,则278/80=3.475),由(2)式计算得到λ=1.628。
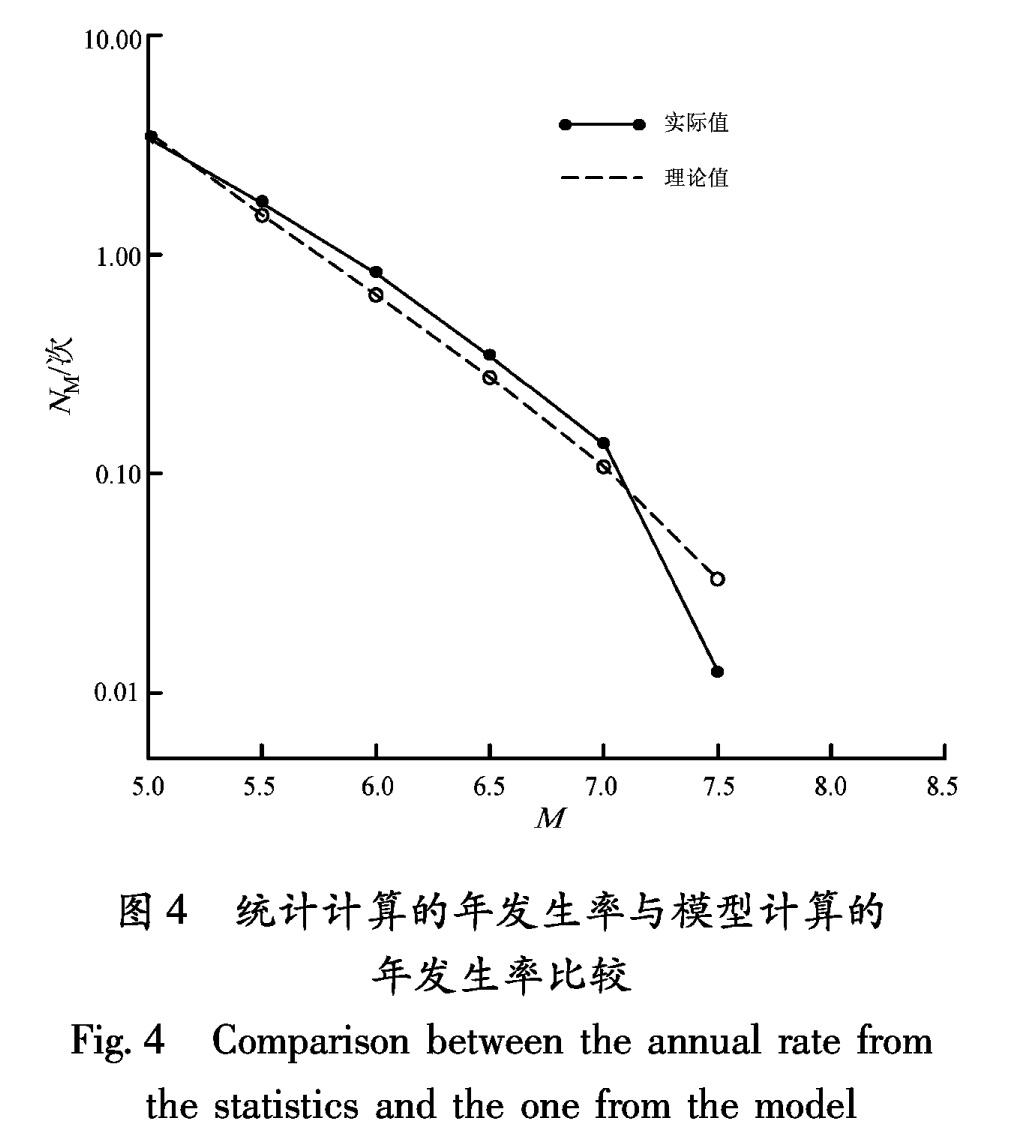
用该模型参数(Mmin=5.0,Mmax=8.0,N(Mmin)=3.475,λ=1.628),由(1)式可计算得到M≥6.0、M≥6.5、M≥7.0地震的年发生率。图4给出了直接统计计算的年发生率(由实际统计的地震次数除以统计时段的时间长度得到)与由模型计算的年发生率(式(1))的比较。由图4可见,对于云南地区的M≥6.0、M≥6.5、M≥7.0地震,由模型计算给出的年发生率均比统计结果偏低20%左右。由于地震活动时间分布上的非均匀性,用不同时段的资料进行统计,其年发生率存在较明显差异; 而通过模型式(1)计算,如果地震目录资料是完整的,这种差异就不大,可近似忽略。
3.2 M≥6.0、M≥6.5、M≥7.0地震的概率模型前文讨论了用1930~2009年云南地区M≥5.0地震目录,基于G—R关系的年发生率和泊松分布模型构建云南地区M≥6.0、M≥6.5、M≥7.0强震的概率预测模型。
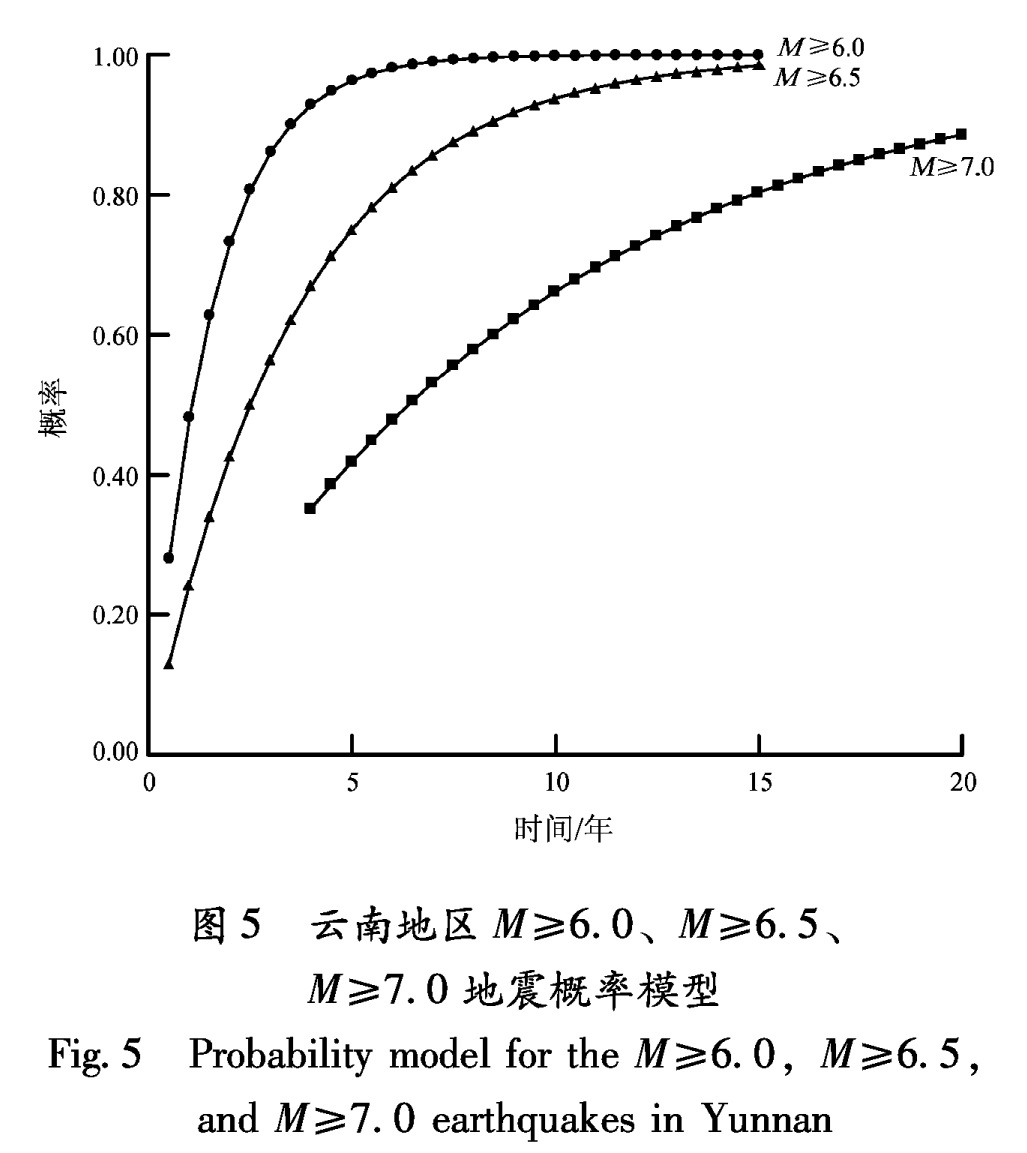
笔者用上述模型参数,由式(3)分别计算给出了云南地区M≥6.0、M≥6.5、M≥7.0地震随间隔时间的概率增长变化曲线(步长为0.5 a)(图5)。应
用该模型,可以根据M≥6.0、M≥6.5、M≥7.0地震的平静时间(间隔时间),给出各震级档地震的危险性的概率水平。例如,从2000年1月15日姚安6.5级地震发生至2010年6月,云南地区M≥6.5地震的平静时间为10.46 a,由该模型给出的M≥6.5地震的危险性概率水平为0.95(95%); 从1996年2月3日丽江7.0级地震发生至2010年6月,M≥7.0地震的平静时间为14.41 a,由该模型给出的M≥7.0地震的危险性概率水平为0.79(79%)。3.3 预测预警指标研究根据前面的分析,M≥6.0地震的平均间隔时间为1.27 a,0.5σ方差线为1.93 a,1.0σ方差线为2.58 a,为了便于表示,分别近似取1.5 a、2.0 a、2.5 a 3个特征时间; M≥6.5地震的平均间隔时间为2.75 a,0.5σ方差线为4.13 a,1.0σ方差线为5.52 a,分别近似取3.0 a、4.0 a、5.5 a 3个特征时间; M≥7.0地震的平均间隔时间为8.21 a,0.5σ方差线为11.54 a,1.0σ方差线为14.87 a,分别近似取8.0 a、11.5 a、15.0 a 3个特征时间。表1给出了这些统计特征时间及相应的概率水平。由此,笔者根据云南地区M≥6.0、M≥6.5、M≥7.0地震间隔时间分布统计特征及概率模型,建立具有概率水平的三级预测预警指标:C(黄)、B(橙)、A(红)(表1)。
(1)M≥6.0地震预测预警指标:当M≥6.0地震的间隔时间(或平静时间)ΔT≥平均间隔时间(1.5 a)时,发布M≥6.0地震黄色预警(C级),概率水平≥0.63; 当间隔时间ΔT≥0.5σ(2.0 a)时,发布M≥6.0地震橙色预警(B级),概率水平≥0.73; 当间隔时间ΔT≥1σ(2.5 a)时,发布M≥6.0地震红色预警(A级),概率水平≥0.81。
(2)M≥6.5地震预测预警指标:当M≥6.5地震的间隔时间ΔT≥平均间隔时间(3.0 a)时,发布M≥6.5地震黄色预警(C级),概率水平≥0.56; 当间隔时间ΔT≥0.5σ(4.0 a)时,发布M≥6.5地震橙色预警(B级),概率水平≥0.67; 当间隔时间ΔT≥1σ(5.5 a)时,发布M≥6.5地震红色预警(A级),概率水平≥0.78。
(3)M≥7.0地震预测预警指标:当M≥7.0地震间隔时间ΔT≥平均间隔时间(8.0 a)时,发布M≥7.0地震黄色预警(C级),概率水平≥0.58; 当间隔时间ΔT≥0.5σ(11.5 a)时,发布M≥7.0地震橙色预警(B级),概率水平≥0.71; 当间隔时间ΔT≥1σ(15.0 a)时,发布M≥7.0地震红色预警(A级),概率水平≥0.80。
按上述预测预警指标,目前云南地区M≥6.5地震平静时间为10.46 a,已处于红色预警(A级)阶段; M≥7.0地震平静时间为14.41 a,还处于橙色预警(B级)阶段,但到2011年2月,将进入红色预警(A级)阶段。
4 讨论和结论
本文给出了云南地区M≥6.0、M≥6.5、M≥7.0地震的间隔时间分布统计特征。结果表明,M≥6.0地震的平均间隔时间约为1.27 a,均方差(σ)为1.31 a,实际间隔时间大于等于平均间隔时间、0.5σ方差线和1.0σ方差线的比例分别为38%、27%和11%; M≥6.5地震的平均间隔时间约为2.75 a,均方差为2.77 a,实际间隔时间大于等于平均间隔时间、0.5σ方差线和1.0σ方差线的比例分别为39%、17%和14%; M≥7.0级地震的平均间隔时间约为8.21 a,均方差6.66 a,实际间隔时间大于等于平均间隔时间、0.5σ方差线和1.0σ方差线的比例分别为36%、27%和18%。由此可见,对于这3个震级档,60%以上的地震均发生在平均间隔时间内。这些统计特征对于认识云南地区6级以上地震的活动性及其预测研究是很有意义的,有助于我们对一次6级以上地震发生后,下一次6级以上地震发生的可能时间有一个基本的判断。间隔时间越长,发震的危险性越大,这是一个基本的统计概念。尤其是当间隔时间超0.5σ方差线或1.0σ方差线时,虽然这类情况出现的比例不高(3个震级档的比例分别为27%,17%,27%或11%,14%,18%),但其更具有显著性,能引起特别的注意。因此,对这部份地震的分析预测可能更具有指标意义。
用1930~2009年云南地区M≥5.0地震目录,基于G—R关系的年发生率和泊松分布模型,构建了云南地区M≥6.0、M≥6.5、M≥7.0共3个震级档地震的泊松概率预测模型。应用该模型,根据M≥6.0、M≥6.5、M≥7.0地震的平静时间(即间隔时间),就可以得到其危险性的概率水平。事实上,对一个地区而言,只要所研究震级地震的年发生率((3)式)没有变化,这就是一个“固定不变”的或者说与时间无关的模型。唯一的变化参量是间隔时间,间隔时间增加,危险性概率就非线性增加(图5)。前面提到,由模型计算得到的年发生率比直接统计计算得到的年发生率低(图4),由其计算所得的概率也低。
本研究中把云南地区M≥6.0、M≥6.5、M≥7.0地震的间隔时间分布统计特征与概率模型结合起来,分别用M≥6.0、M≥6.5、M≥7.0的3个统计特征时间(平均间隔时间、0.5σ方差线和1.0σ方差线),建立了具有概率水平的三级预测预警指标:C(黄)、B(橙)、A(红)。将其应用于云南地区当前的地震危险性预测,可以得到M≥6.5地震的平静时间为10.46 a,已处于红色预警(A级)阶段; M≥7.0地震的平静时间为14.41 a,处于橙色预警(B级)阶段,但到2011年2月,将进入红色预警(A级)阶段。可见,云南地区当前或未来一段时间内,发生6.5级以上或7级以上地震的危险性概率水平分别≥0.95或≥0.79。从以上统计分析可知,该套指标只适用于约40%的M≥6.0、M≥6.5、M≥7.0地震,因为约60%以上的地震均发生在平均间隔时间内。换言之,只有当3个震级档的地震间隔时间大于平均间隔时间,才能用该套指标进行分析和判定。
- 国家地震局震害防御司.1995.中国历史强震目录(公元前23 世纪—公元1911 年)[M].北京:地震出版社.
- 国家地震局震害防御司.1999.中国近代地震目录(公元1912 年—1990 年)[M].北京:地震出版社.
- 黄玮琼,李文香,曹学峰.1994.中国大陆地震资料完整性研究(之二)[J].地震学报,16(4):423-432.
- 皇甫岗,李忠华.2010.20世纪云南地区地震记录完全性评价[J].地震研究,33(1):1-6.
- 任俊杰,陈虹.2004.东昆仑断裂带地震复发周期与发震概率研究[J].大地测量与地球动力学,24(3):51-56.
- 苏有锦,李忠华,刘祖荫,等.2001.20世纪云南地区M≥5.0级地震活动的基本特征[J].地震研究,24(1):1-8.
- 易桂喜,闻学泽,徐锡伟.2002.川滇地区若干活动断裂带整体的强地震复发特征研究[J].中国地震,18(3):267-296.
- 张永庆,谢富仁,王峰.2007.乌鲁木齐地区活动断裂强震复发概率模型研究[J].地震地质,29(4):776-786.
- Dong W M,Bao A B,Shah H C.1984.Use of maximum entropy principle in earthquake recurrence relationships[J].BSSA,74(2):725-737.
- Field E H.2007.A summary of previous working groups on California earthquake probabilities[J].BSSA,97(4):1033-1053.
- Kagan Y Y,Jackson D D.1999.Worldwide doublets of large shallow earthquakes[J].BSSA,89:1147-1155.
- Matthews M V,Ellsworth W L,Reasenberg P A.2002.A brownian model for recurrent earthquakes[J].BSSA,92(6):2233-2250.
- Sun J C,Pan T C.1995.The Probability of very large earthquakes in Sumatra[J].BSSA,85(4):1226-1231.
- Zöller G,Hainzl S.2007.Recurrence time distributions of large earthquakes in a stochastic model for coupled fault systems:The roles of fault interaction[J].BSSA,97(5):1679-1687.