基金项目:国家自然科学基金(51078273)资助.
(1.同济大学 结构工程与防灾研究所,上海 200092; 2.同济大学 上海防灾救灾研究所,上海 200092; 3.国核工程有限公司,上海 200092)
(1.Research Institution of Structural Engineering and Disaster Reduction,Tongji University,Shanghai 200092,China)(2.Shanghai Institution of Disaster Prevention and Relief,Tongji University,Shanghai 20092,China)(3.National Nuclear Engineering Limited Company,Shanghai 20092,China)
seismic motion; rotational components; numerical simulation method
备注
基金项目:国家自然科学基金(51078273)资助.
列举了多次地震中的地震动转动现象,概括了国内外对地震动转动分量的产生、传播、合成方法及其对结构的作用等方面的研究成果。还介绍了由地震动平动分量计算转动分量的弹性波动方法,并讨论了其局限性; 还介绍了欧洲规范对转动分量的部分规定,指出有必要在结构抗震设计中考虑转动分量的作用。此外,在转动分量的产生、对结构的作用及数值模拟方面还做了一些假设与解释。
An intuitionistic description of the seismic rotational phenomena is listed firstly,and then the research results both at home and abroad in several fields are summarized,such as the generation,propagation of the seismic rotational components and its effects on structure.The elastic wave method used to calculate the rotational components through translational components is introduced and its limitation is discussed.Some parts of rules of Eurocodes about rotational components are referred and the necessity of adding the seismic rotational effects in the design of structures for earthquake resistance is pointed out.Further,some hypotheses and explanations in rotational component's generation,effects on structure,and structure's numerical simulation are proposed.
引言
2009年,美国知名的地学类期刊Bulletin of the Seismological Society of America出版了关于地震动转动问题的专辑,这对我们学习和研究地震动转动问题有很大帮助(Lee et al,2009)。
多次历史地震记载中都有转动破坏现象的记录。1783年意大利的Calabria地震、1897年印度Assam地震、1906年美国旧金山地震和2008年中国四川汶川地震,都有不同形式的转动破坏现象。Kozák(2009)总结了12次地震中的转动破坏现象,发现在细长高耸的建筑中出现较多转动破坏,如烟筒、教堂上的装饰、方尖碑、雕像、十字架等。同时,也不乏大型结构的扭转破坏,如1894年日本Shonai地震时钟楼的扭转破坏和1897年印度Assam地震中20 m高的方尖碑的扭转破坏(图1)。有的扭转反应是由地面的扭转引起的(Hart et al,1975),如1971年加州地震中洛杉矶一高层建筑的扭转破坏,而有的则是因为不同步变形引起的(Bycroft,1980; Trifunac et al,1994),如地震中很多大桥的垮塌是由桥墩纵向的不同步变形引起的。生命线工程中大多管线的破坏则是由土体的不均匀变形引起的,这和地震中的摇摆和扭转分量也都有关系(Ariman,1981; Trifunac,1998)。这些现象也说明地震中转动的能量是很大的,需要引起人们的注意。Yang等(2010)在
2008年汶川8.0级地震震害调查中,对江油市太白公园一曲径桥桥栏上的雕塑灯座扭转破坏现象做了调查,并通过计算,初步解释了产生这一扭转现象的原因(图2)。图1 1897年印度阿萨姆地震方尖碑破坏形态(Lee et al,2007)
Fig.1 Rotation of obelisk segments in the 1897 Assam earthquake(Lee et al,2007)1 地震动转动分量的产生及其传播
1.1 转动破坏现象在18世纪,人们就注意到地震中的转动问题,并留下关于转动的报道,这比现代地震学学科的开启还要早近百年的时间(Vivenzio et al,1783; Trifunac,2008)。因为摇摆对结构的破坏与平动造成的破坏相差不多,震后很难分辨破坏是由摇摆分量还是由平动分量造成的,所以,对转动分量造成破坏的观察只限于扭转破坏现象。小震发生时,在仅能感到轻微震动的震中地区,很少发现转动现象; 大震发生时,在远离震中、震动衰减较大、地面震动较缓和的地区,转动现象也难以察觉,但有迹象表明这些地区存在转动现象; 在地震动很强的地方,即使距震中很远,结构的转动现象也很明显。在地震中观察到转动现象的人描述说,首先看到的是一般振动现象,随后才出现转动现象。Reid(1910)至今还没有发现地震一发生就出现转动现象的报道。
1.2 转动现象研究的简单回顾据Ferrari(2006)和Kozák(2006)介绍,Robert Mallet对地震动转动的研究贡献很大,他研究了地面物体的转动情况,分析了产生转动现象的原因,并合理解释了1857年意大利Basilicata地震中的一些扭转现象。但Reid(1910)认为,是Hoffmann(1838)首先提出地震转动分量的理论 Hoffmann F.1838.Nachgelassene Werke.(2)230pp.。Reid(1910)认为,在地震动的各种成分中,有沿某条轴转动的成分,但这种波是不可能存在的,因为这种波不能再像弹性波一样传播,否则它会分解成各种不同传播速度的压缩波或者扭转波,并很快消失。Gutenberg(1927)也提到,地震动的旋转分量是不能传播的,如果在震源处产生旋转,它会很快衰减。
1.3 转动分量的解释对于转动分量产生的原因,有很多不同的解释。弹性波理论认为转动不是因为有扭矩存在,而是因为颗粒的不对称变形,如图3所示; Knopoff 等(2009)用应力降速率等震源机制分析转动产生的原因,结果发现断层中的扭矩不平衡可以产
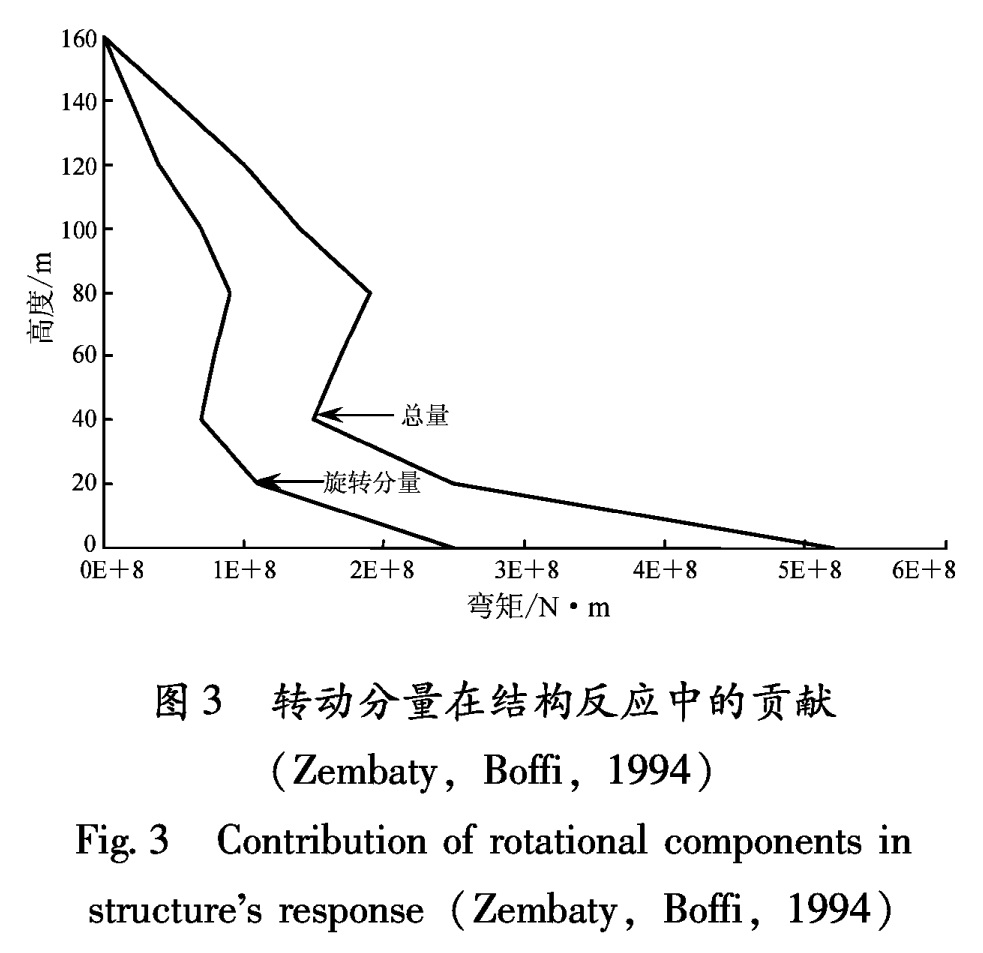
生转动并使场地产生扭转变形; Trifunac(1972)模拟了2维土—结构相互作用,结果显示结构对土体的作用可以产生很强的地面扭转。这说明转动分量产生原因的复杂性。现在还不清楚转动分量主要是由震源释放的转动能量还是由平动分量形成,转动仅仅是场地的扭动还是有更深层的原因,这也需要进一步研究。震源释放转动能量的理论与前面叙述的转动不能以波的形式传播的理论相冲突,因而本文对此暂不讨论。图3 转动分量在结构反应中的贡献(Zembaty,Boffi,1994)
Fig.3 Contribution of rotational components in structure's response(Zembaty,Boffi,1994)摇摆分量相对容易解释,例如地震波在地表传播过程中,地表的高低起伏会出现近似摇摆的现象。但地震观测告诉我们扭转现象十分复杂。有人认为,面波中的勒夫波扭动传播,它会使介质中质点的振动在水平方向和波前进方向的分量耦合后产生扭转分量(李杰,李国强,1992)。在研究地震动扭转时有些问题值得思考,如扭转的各个点是不是沿着不同的相互平行的轴转动?从波动理论来看,体波中的压缩波在土体中传播时,土层内会出现压缩和张拉交替的情景,不同方向传来的P波是否会让土体产生转动?地震中出现的扭转大小和振动的大小正相关:震级大,断层长度长,从两个不同的破裂点处传出的压缩波相交一点的角度大,形成的旋转是否就大?地震动的平动遇到建筑物(土—结构相互作用)会形成转动,那么地震波传到不同的地质临界处,是否也会产生旋转呢?出现扭转破坏的全对称构筑物的半径大多较小,比如烟囱,我们应该如何考虑其对底面积较大的建筑物的作用?
2 计算转动分量的主要方法
2.1 转动分量的记录人类在19世纪就掌握了记录平动分量的技术。因为地震动的转动影响较小,而记录转动的仪器又很复杂,所以转动分量在研究中逐渐被忽略(Galitzin,1902),直到1960年,地震工程学界才认识到地震动的转动成分对结构的反应有很大贡献(Trifunac,Giev,2006)。到20世纪80年代又有人提出三个平动、三个转动的观点,人们对转动分量的研究逐渐变多。目前对转动分量的时程记录仍然很少,主流方法是通过平动求转动。两点差法是指在很小的范围内布置多台地震仪记录水平分量,用两点间的平动位移差或平动加速度差除以两点间距离就是相应的转角或角加速度,思路简单可靠,但因为需要布设台阵故而不经济。我们可以用两点差法来验证从平动分量到转动分量的理论的正确性。
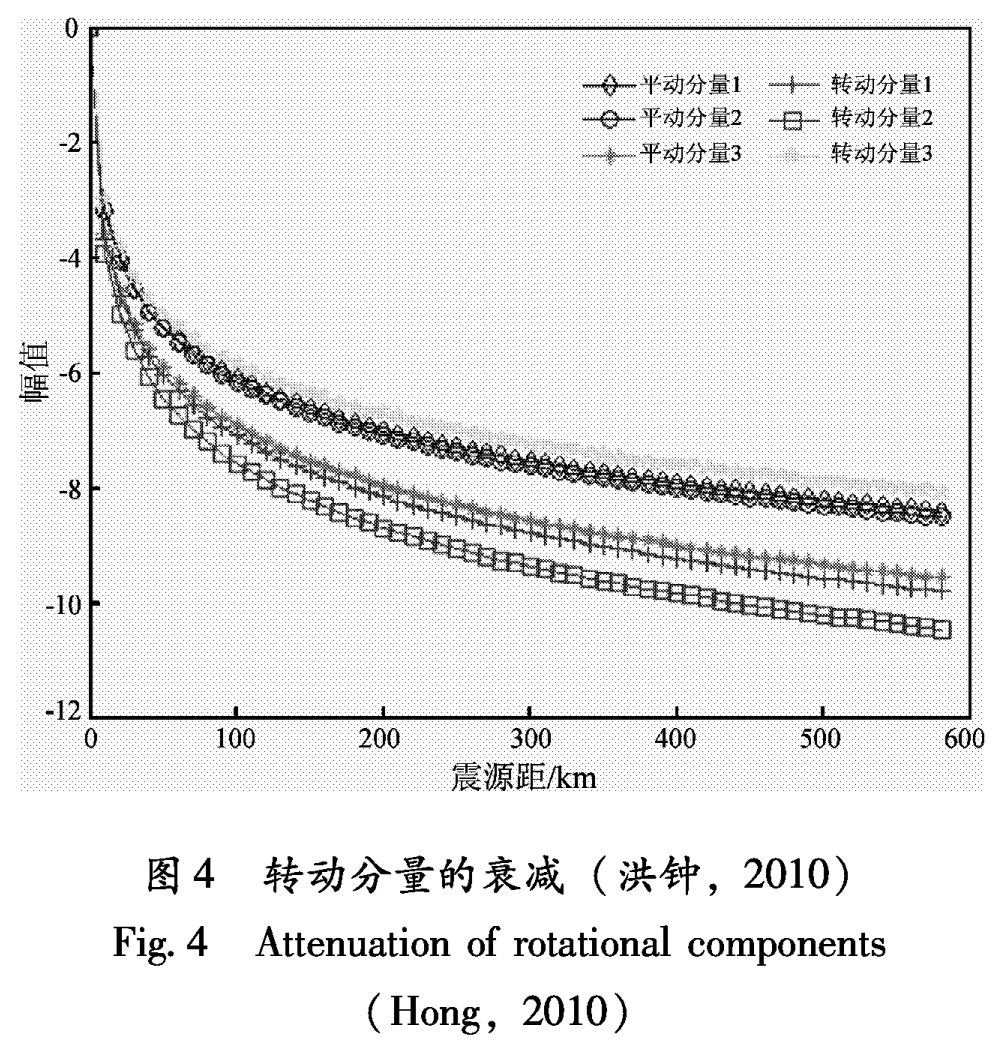
2.2 弹性波动理论解析弹性波动理论认为介质颗粒在地震中会发生不对称变形,如图3所示,Newmark(1969)首先建立了地震动转动分量和平动分量的关系(Li et al,1997)。场地土是分层的,不同频率的波有不同的传播速度并在不同界面有不同的入射角,从而影响视波速的大小。Trifunac(1982)首先认识到体波波速和入射角的频散效应对分析结果的影响,他所提方法目前运用得最多(洪钟,2010)。其主要步骤如下:
假设u1、u2、u3是地震动两个水平方向和一个竖直方向的位移分量,φ1、φ2、φ3为对应的绕三条轴的转动分量,于是:
(1)对u1(t)、u2(t)、u3(t)作傅立叶变换得到u1(ω)、u2(ω)、u3(ω);
(2)考虑主频方向的影响,设主轴角为θ,将得到的u1(ω)、u2(ω)、u3(ω)以及视波速C代入公式
{φ1(ω)=(iω)/Cu3(ω)sinθ,
φ2(ω)=(iω)/Cu3(ω)cosθ,
φ3(ω)=1/2·(iω)/C[u2(ω)cosθ-u1(ω)sinθ],
(1)
求得转动分量傅氏谱φ1(ω)、φ2(ω)、φ3(ω)。其中θ为主频角,i=(-1)1/2,ω为频率,C=vT(f)/sinα,VT(f)为等效群速度,α为体波入射角。
(3)对φ1(ω)、φ2(ω)、φ3(ω)作逆傅立叶变换,取实部,即可得转动分量时程曲线。
王君杰和胡聿贤(1991)用两点差法对行波法进行了验证,证明行波法有一定的精度,且此精度和震中距有关,震中距越大,行波法精度越高。金星和廖振鹏(1991)阐述了估计水平视波速的方法; 孙士军和陈国兴(1998)提出了用实际记录的加速度时程估计地震波入射角的方法; 李宏和孙立晔(2001)用类似的方法计算过地震面波产生的转动分量; Che和Luo(2010)也用这种方法计算了台湾集集地震的转动分量,Rutenberg和Heidebrecht(1985)、Castellani和Boffi(1986,1989)、孙士军和陈国兴(1991)、Tso和Hsu(1997)、Giev和Trifunac(2009)还尝试过用类似的方法计算扭转分量和摇摆分量的反应谱。
但弹性波动理论方法有一定缺陷,它假设弹性波是在理想的各向均质同性的水平层状介质中传播的,将两点间的相对运动近似地看成了直线,在地震作用中介质不会产生塑性变形。Giev(2009)模拟了S波在土层中的传播,结果表明,在入射波进入土层的初始阶段土层就发生了破坏,破坏形成的时间比地震波穿过土层的时间还短。地表土、沉积物及其一些风化岩石在强震时会出现非线性变形,人们在震害调查中也发现土的非线性变形很严重,这会增大地面的转动现象。Bouchon和Aki(1982)、Lee等(2009)均用弹性方法计算了强震中的转动分量,所得的结果和观察到的现象相差几个数量级,说明用这种方法估计强震的转动分量时,会低估几个数量级,其原因可能是近场场地出现非线性变化,造成数值计算方法的误差。
从公式(1)不难看出,若不考虑视波速的频散效应,两摇摆分量的频谱特性及衰减关系应和垂直分量的衰减相同,扭转分量的频谱特性及衰减和两水平分量的衰减相同。洪钟(2010)考虑了视波速的频散效应对转动分量大小影响后得到的衰减结果如图4所示。从图中可看出,地震动转动分量不会很快衰减,因此,必须对转动分量有足够的重视。
2.3 转动分量形成机制的其他解释Zembaty(2009b)分析了地震波体波和面波中的各个成分对形成转动分量的贡献,他发现摇摆分量来自于P波、SV波和瑞利面波,扭转分量来自于SH波和勒夫波,各个分量叠加后形成转动分量。但地震动是非平稳过程,从地震动时程中分离出各种成分并非易事。目前在中远场记录到的转动分量和用弹性波动理论得到的结构转动反应还相差两个数量级,Takeo和Ito(1997)认为这是因为数值模拟方法忽略了一种可能的现象——较大的转动速度是由断层破裂速度的非均匀引起的。他们基于转动和平动观测记录,得到平
动与转动之间的关系,并用这种关系由平动分量计算转动分量,但这种方法的困难在于转动记录的缺乏。3 转动分量对结构的影响
3.1 结构的扭转破坏结构的扭转破坏未必是由地震动扭转分量造成的,非对称的结构在平动分量作用下也会产生转动破坏(Yang et al,2010)。地震发生时完全对称的比较大的长细结构在左右摇摆中呈现不对称,再受到冲击后,就会发生扭转破坏。后来的研究发现在结构地震反应中,扭转分量(Luco,1976; Lee,Trifunac,1985)和摇摆分量(Lee,Trifunac,1987)对结构反应的贡献是很大的。研究表明,近场地震波的转动成分较大,其对结构的影响也很大,甚至对结构的线性和非线性的变形都起到了控制作用(Jalali,Trifunac,2008)。Werner等(1979)、Trifunac和Giev(2006)、Jalali和Trifunac(2008)分析了转动分量对结构的作用,他们都认为转动分量在结构构件中可以产生很大的剪力和弯矩。但是,因为缺乏转动分量记录等原因,许多国家在结构的抗震设计中都未考虑转动作用。
3.2 欧洲规范关于转动荷载的规定鉴于转动分量的重要性,欧洲已将地震动转动荷载纳入设计规范《EC8.1.EN 1998-1 Eurocode 8》和《EC8.6.EN 1998-6 Eurocode 8》(以下简称《规范》)。《规范》规定需要考虑转动荷载的结构是塔形建筑,包括水塔、电视塔、桅杆、烟筒、灯塔等,对于钢筋混凝土结构或钢结构的烟筒,《规范》还有特殊规定。《规范》建议高度大于80 m、设计加速度不小于0.25 g的建筑物也要考虑转动荷载,并强调考虑土—结构相互作用,对于长细比很大的结构要考虑二阶效应。结构对转动荷载的反应计算采用时程法和反应谱法。采用反应谱法时,三个方向的转动加速度取与当地剪切波速相关的经验值。Zembaty(2009a)认为扭转分量对细长结构的作用很小,只是考虑到《规范》的完整性才将其纳入《规范》。Zembaty和Boffi(1994)按欧洲规范规定的反应谱法计算了160 m高的钢筋混凝土烟筒三条转动分量及地震六分量作用下的反应,还比较了转动分量在总反应中的贡献,结果如图3所示。从图中可看出,对于高耸结构来说,转动分量对结构反应的贡献几乎和水平分量相当。这一点很容易理解,转动中的摇摆分量会对高耸结构产生很大的破坏。
3.3 转动作用的特点Park(2007)认为:结构在地震时的转动可来自:(1)地震波的转动分量;(2)土—结构相互作用;(3)结构由于惯性力引起的相对变形。我国在抗震设计中不考虑转动成分,这在近场区域会低估结构的地震反应。Tso和Hsu(1977)、Rutenberg和Heidebrecht(1985)、 Trifunac(2009b)对扭转分量反应谱的研究结果表明,反应谱在0.2~0.6 s之间是最高的平台。结构的扭转自振周期处于这一周期区间的建筑更容易受扭转分量的影响。1~50层建筑与土相互作用产生的扭转的频率在0.1~10 Hz之间(Trifunac,2009b)。陈国兴等(1999)用反应谱分析法得出,转动分量对结构角部构件的反应影响较大。Trifunac(2009a)指出,近场处即便是很简单的结构,忽略转动分量的作用可能会严重低估结构响应,一个合理的结构设计,考虑并理解转动分量对结构响应的贡献非常重要。
王君杰(1995)计算得出,扭转分量对结构反应的贡献与结构的高度和长细比有关。扭转分量对烟筒类的高柔建筑的作用较小,但震害中的扭转破坏,如烟筒、方尖碑等高柔建筑占绝大部分。这一差别可能源自地震扭转分量的真实作用方式和计算加载方式的不同。Trifunac(2008)将土—结构相互作用作为转动分量产生的机制。在高楼林立的城市,地震时高大的建筑所产生的转动分量会对周边的小型建筑产生影响,这可用以说明地震动的转动分量在城市中的破坏要比在其他地区更大。当涉及到大跨度桥梁时,因为不同桥墩很可能会沿着不同的中心旋转,这会使桥墩的运动不同步,这对桥梁的损害可能比考虑两墩之间地震动平动成分的差异带来的损害还要严重。当然,这仅仅是推理,正确与否还有待深入研究。
4 结语
(1)不同的理论对转动分量产生机制的解释与计算方法有所不同,但都认为地震动转动分量是结构在地震中不可避免的荷载。
(2)用经典的弹性波动方法解释近场转动现象还不够完善,正如Lee等(2007)所说,应该研究更好的方法来弥补这一空白。
(3)由于缺乏转动分量记录,人们对地震动转动分量和结构的转动响应的实际值所知甚少,应通过监测、试验、理论分析等多种方法研究地震动转动分量和结构的转动响应。鉴于欧洲规范的经验,今后我国的抗震设计规范中有必要逐步考虑地震动转动作用的影响。
- 陈国兴,孙士军,宰金珉.1999.多维相关地震动作用下结构反应的反应谱法[J].南京建筑工程学院学报,51(4):17-22.
- 洪钟.2010.地震动转动分量研究[D].上海:同济大学.
- 李宏男,孙立晔.2001.地震面波产生的地震动转动分量研究[J].地震工程与工程震动,21(1):15-23.
- 李杰,李国强.1992.地震工程学导论[M].北京:地震出版社.
- 金星,廖振鹏.1991.地面转动分量的工程预测[J].地震工程与工程振动,11(4):11-18.
- 孙士军,陈国兴.1998.地面运动转动分量的合成方法[J].地震学刊,(1):19-24.
- 孙士军,陈国兴.1991.地面转动分量的标准反应谱[J].南京建筑工程学院学报,(4):10~14.
- 王君杰,胡聿贤.1991.地震动旋转分量的研究[J].地震工程与工程振动,11(2):1-10.
- 王君杰.1995.地震动扭转分量对薄壁柱壳结构的影响[J].地震学报:17(2):217-222.
- Ariman T,Muleski G E.1981.A review of the response of buried pipelines under seismic xcitation[J].Earthq Eng Struct Dyn,9:133-151.
- Bouchon M,Aki K.1982.Strain and rotation associated with strong ground motion in the vicinity of earthquake faults[J].Bull Seismol Soc Am,72(5):1717-1738.
- Bycroft G N.1980.Soil-foundation interaction and differential ground motions[J].Earthq Eng Struct Dyn,8:397-404.
- Che W,Luo Q F.2010.Time-frequecy response spectrum of rotational ground motion and its application[J].Earthquake Science,23(1):71~77.
- Castellani A,Boffi G.1986.Rotational components of seismic motion[J].Earthq Eng Struct Dyn,14:751-767.
- Castellani A,Boffi G.1989.On the rotational components of seismic motion[J].Earthq Eng Struct Dyn,18:785-797.
- EC8.1.EN 1998-1 Eurocode 8:Design of structures for earthquake resistance; Part 1:General rules,seismic actions and rules for buildings[S].February 2005,European Committee for Standardization,Management Centre:rue de Stassart,36 B-1050 Brussels.
- EC8.6.EN 1998-6 Eurocode 8:Design of structures for earthquake resistance; Part 6:Towers,masts,and chimneys[S].September 2005,European Committee for Standardization,Management Centre:rue de Stassart,36 B-1050 Brussels.
- Ferrari G.2006.Note on the historical rotation seismographs[J].Earthquake Source Asymmetry,Structural Media and Rotation Effects,R.Teisseyre,M.Takeo and E.Majewski(Editors),Springer,Heidelberg,367-376.
- Galitzin B.1902.Uber seimometrische beobahtungen[J].Izv Postyann Tsent Seism Komm,1(1):101-183.
- Giev V,Trifunac M D.2009.Transient and permanent rotations in a shear layer excited by strong earthquake pulses[J].Bull Seismol Soc Am,99(2B):1 391-1 403.
- Gutenberg B.1927.Grundlagen der Erdbebenkunde.University of Frankfurt a M.
- Hart G C,DiJulio M,Lew M.1975.Torsional response of high-rise buildings[J].ASCE,101:397-414.
- Jalali R,Trifunac M D.2008.A note on strength reduction factors for design of structures near earthquake faults[J].Soil Dyn Earthq Eng,28(3):212-222.
- Knopoff L,Y T Chen.2009.Single-couple component of far-field radiation from dynamical fractures[J].Bull Seismol Soc Am.99(2B):1091-1102.
- Kozák J T.2006.Development of earthquake rotational effect study[M].Teisseyre R.Takeo M.Majewski E.Earthquake Source Asymmetry,Structural Media and Rotation Effects.Springer,Heidelberg,3-10.
- Kozák J T.2009.Tutorial on earthquake rotational effects:historical examples[J].BSSA,99(2):998-1010.
- Lee V W,TrifunacM D.1985.Trifunac.Torsional accelerograms[J].Soil Dynamics and Earthquake Engineering,14(3):132-139.
- Lee V W,Trifunac M D.1987.Rocking strong earthquake accelerations[J].Soil Dynamics and Earthquake Engineering,6(2):75-89.
- Lee W H K,Celebi M,Todorovska M I,et al.2007.Rotational Seismology and Engineering Applications:Proceedings for the First International[C].Workshop.Menlo Park,California,U.S.A.
- Lee W H K,Celebi M,Todorovska M I,et al.2009.Introduction to the special issue on rotational seismology and engineering applications[J].BSSA,(2B):945-957.
- Lee V W,Trifunac M D.2009.Empirical scaling of rotational spectra of strong earthquake ground motion[J].BSSA,99(2B):1378-1390.
- Li Hongnan,Sunarez L E,Singh M P.1997.Rotational Components of Earthquake Ground Motions[J].Earthq Eng Struct Dyn.17(2):37-51.
- Luco J E.1976.Torsional response of structures to obliquely incident seismic SH waves[J].Earthq Eng Struct Dyn.4:207-219.
- Lee W H K,CelebiM,Toberovska MI.2007.Rotational Seismology and Engineering Applications[C]//Proceedings for the First International Workshop.California,U.S.A,September 18-19.
- Newmark N M.1969.Torsion in symmetrical buildings.3:19-32.
- Reid H F.1910.The California Earthquake of April 18,1906:The mechanics of the earthquake,report of the State Earthquake investigation Commission[R],Carnegie Institution of Washington,2:43-47.
- Rutenberg A,Heidebrecht A C.1985a.Response Spectra for Torsion.Rocking and Rigid[J].13,543-557.
- Rutenberg A,Heidebrecht A C.1985b.Rotational Ground Motion and Seismic Codes[J].Canadian Journal of Civil Engineering,12:583-592.
- Takeo M.2006.Ground rotational motions recorded in near-source region of earthquakes,in Earthquake Source Asymmetry[M]//Structural Media and Rotation Effects,Springer,New York,Chapter 12:157-167.
- Takeo M,Ito H I.1997.What can be learned from rotational motions excited by earthquakes[J].Geophys J Int,129:319-329.
- Trifunac M D.1972.Interaction of a shear wall with the soil for incident plane SH waves[J].Bull Seismol Soc Am.62(1):63-83.
- Trifunac M D.1982.A note on rotational components of earthquake motions on ground surface for incident body waves[J].Soil Dynamics and Earthquake Engineering:1(1):11-19.
- Trifunac M D,Todorovska M I,Ivanovic S S.1996.Peak velocities,and peak surface strains during Northridge,California,earthquake of 17 January 1994[J].Soil Dyn Earthq Eng,15(5):301-310.
- Trifunac M D,Todorovska M I.1997.Northridge,California,earthquake of 17 January 1994:density of pipe breaks and surface strains[J].Soil Dyn Earthq Eng 16(3):193-207.
- Trifunac M D,Todorovska M I.1998.Nonlinear soil response as a natural passive isolation mechanism-the 1994 Northridge,California,earthquake[J].Soil Dyn Earthq Eng,17(1):41-51.
- Trifunac M D.2006.Effects of torsional and rocking excitations on the response of structures[J].Earthquake Source Asymmetry.Structural Media and Rotation Effects,R.Teisseyre,M.Takeo and E.Majewski,Springer,Heidelberg:569-582.
- Trifunac M D,Giev V.2006.Response spectra for differential motion of columns,paper II:Out-of-plane response[J].Soil Dyn Earthq Eng,26(12):1149-1160.
- Trifunac M D.2009a.75th Anniversary of strong motion observation-A historical review Soil Dyn[J].Soil Dynamics and Earthquake Engineering.29(4):591-606.
- Trifunac M D.2009b.Review:rotations in structural response[J].Bull Seismol Soc Am.99(2B):968-979.
- Trifunac M D.2009b.The role of strong motion rotations in the response of structures near earthquake faults[J].Soil Dyn Earthq Eng.29(2):382-393.
- Trifunac M D.2008.Buildings as sources of rotational waves[R]//R.Teisseyre,H.Nagahama and E.Majewski,Physics of Asymmetric Continuum:Extreme and Fracture Processes[R].Springer,Heidelberg,Germany.
- Tso W K,Hsu T J.1977.Torsional Spectrum for Earthquake Motions[J].Earthquake 6:375-382.
- Vivenzio G.1783.Istoria e teoria dǒ tremuoti in generaleed in particulare di quelli della Calabria'e di Messina del[J].MDCCLXXXIII,Napoli,Italy.
- Werner S D,Lee L C,Wong H I.1979.Structural response to traveling seismic waves[J].J Struct Div.ASCE 105,no.ST12,2547-2564.
- Yang F,Luo Q F,Che W.2010.Torsional phenomena in 2008 great Wenchuan earthquake[J].Earthquake Science:23(1):79~85.
- Zembaty Z.2009a.Rotational seismic load definition in Eurocode 8,part 6,for slender tower-shaped structures[J].Bull Seismol Soc Am,99(2B),1483-1485.
- Zembaty Z.2009b.Tutorial on surface rotations from wave passage effects:stochastic spectral approach[J].Bull Seismol Soc Am,99(2B),1040-1049.
- Zembaty Z,Boffi G.1994.Effect of rotational seismic ground motion on dynamic response of slender towers[J].Eur Earthq Eng,8:3-11.