基金项目:中国地震局“小江断裂带的中长期地震潜势定量研究”项目(200708035)资助.
(Earthquake Administration of Yunnan Province,Kunming 650224,Yunnan,China)
Qc-value of coda; Aki's singlescattering attenuation model; the Xiaojiang Fault Zone
备注
基金项目:中国地震局“小江断裂带的中长期地震潜势定量研究”项目(200708035)资助.
利用小江断裂带及邻区10个数字地震台记录到的地震波形资料,采用Aki单次散射模型,计算了各台站半径60 km范围内地震尾波Qc值,分别拟合得到10个台站的尾波Qc和η值,并用10个台站的平均结果得出了小江断裂带及邻区尾波Qc值与频率的关系。结果 表明,小江断裂带及邻区总体上属低值Qc区; 尾波Qc值空间差异较大,小江断裂带中段为低Qc值,明显低于北段和南段的Qc值。研究了尾波Qc值在时间上的变化与中强地震的关系。
The coda-wave attenuation factor Qc in the Xiaojiang Fault Zone is estimated through the Aki's single-scattering attenuation model based on the seismic events from January 2000 to December 2009 recorded by 10 regional digital seismic stations.The events are situated within 60 km from the stations.The relation between Qc and f at the 10 stations are fittted as Qc(f)=Q0f0.81.The Qc-value in the Zone is lower than the ones in the other areas of Yunnan.The Qc-value in the middle part of the Zone is much lower than the ones in the north and the south part of the Zone.The relationship between the temporal variation of Qc-value and the mid-strong earthquakes is studied too.
引言
小江断裂带是云南地区一条重要的活动断裂带,是川滇菱形块体的东南边界。该断裂带北部与四川则木河断裂相连,南部被红河断裂所截。全长约450 km,在东川以南分成东、西两支,相距约20 km,东支和西支平均左旋位移速率为6 mm/a。小江断裂带上的地震以频度高、强度高著称,如云南省有记载以来最大的地震——1833年嵩明8.0级大地震就发生在该断裂带上。
地震尾波Qc值是表征某个地区构造活动的指标之一,其变化反映了构造应力的变化。国内外地震学家从不同方面对Qc值开展了大量研究,如运用尾波衰减的时空特征探讨地壳介质的非均匀性、尾波Qc值空间分布与区域构造活动性的关系、大震前后尾波Qc值随时间变化在地震预测中的应用研究等(Peng et al,1968; Xie,Nuttli,1988; Beroza et al,1995; 秦嘉政,阚荣举,1986,秦嘉政等,1995; Yoshihiro et al,2000; 王伟君,刘杰,2004; 马宏生等,2006; 李琼等,2007)。
随着云南地区数字地震台网的建立,地震工作者获得了大量的数字地震波形记录资料,从而得以对区域尾波衰减特征及其与区域构造的关系进行较为精细的研究。笔者利用位于小江断裂带及邻区的10个数字地震台站记录到的近场数字地震波形资料,采用Aki的尾波单次散射模型,计算了各台站60 km范围内的地震尾波Qc值,研究了小江断裂带及邻区Qc值空间分布特征,Qc值时间变化与中强地震的可能关系。
1 计算方法
依据S波单次反射模型,尾波峰值振幅A(f,t)与尾波流逝时间t满足
A(f,t)=S(f)t-1e-πft/Qc.(1)
其中,A(f,t)为台站观测谱; S(f)代表尾波波源因子,与震源、频率有关; f为尾波频率; t为发震时间与S波到时差,根据经验,尾波开始于2倍的S波走时,即t>2R/β(R为震中距,β为S波速度); Qc为尾波衰减系数。
对式(1)取对数,可得
ln(A(f,t)*t)=lnS(f)-πft/Qc.(2)
可以看出式(2)的右边是时间t的直线方程,我们可以从某个地震记录在某一频率上测出A(f,t)和t,即可以求出直线的斜率K,从而可以得到品质因子
Qc(f)=πf/k.(3)
由式(3),可以求出不同频率的尾波Qc值,利用Qc(f)=Q0f η,可以拟合求出Qc与频率f的关系。
2 资料处理及计算过程
笔者选取小江断裂带及其周边10个数字地震台的记录资料进行计算(表1)。每个台站均安装FBS-3A型中长周期三分向速度地震仪,这些地震仪在0.0~20 Hz频段具有速度平坦的响应,信号采样率为50 Hz。在这10个台站中,昆明、通海、弥勒、马龙、易门、禄劝、东川和昭通8个台站自2000年1月以来有波形记录,巧家台自2004年10月以来波形记录,建水台自2008年1月以来有波形记录。图1给出了研究区台站分布图和2000年1月至2009年12月2.5级以上地震震中分布。笔者以台站为圆心,60 km为半径,选取2.5级以上地震,对这些地震波形资料进行筛选、整理,从中挑选出信噪比高、尾波持续时间相对长且振幅不饱和、干扰小且S波清晰的地震事件。
资料处理及计算过程如下:
第一步,使用高斯滤波器对原始数据进行滤波,共计算7个中心滤波频率点,分别为3.0 Hz、4.0 Hz、 5.5 Hz、 8.0 Hz、 10.0 Hz、 12.0 Hz、18.0 Hz。
第二步,去噪和滑移计算。从S波到时开始,对滤波后的数据,取窗长为2 s,以0.8 s间隔滑动计算,求出不同时间点(以窗的中心点为当前时间点)的平均振幅。
第三步,选择拟合开始点和窗长,用最小二乘法计算各个频率点的Qc值。
图2给出了计算尾波Qc值的一个例子。图2a-1是通海台2003年4月13日20时50分ML3.0地震原始波形的垂直分量记录,其下是3.0 Hz、
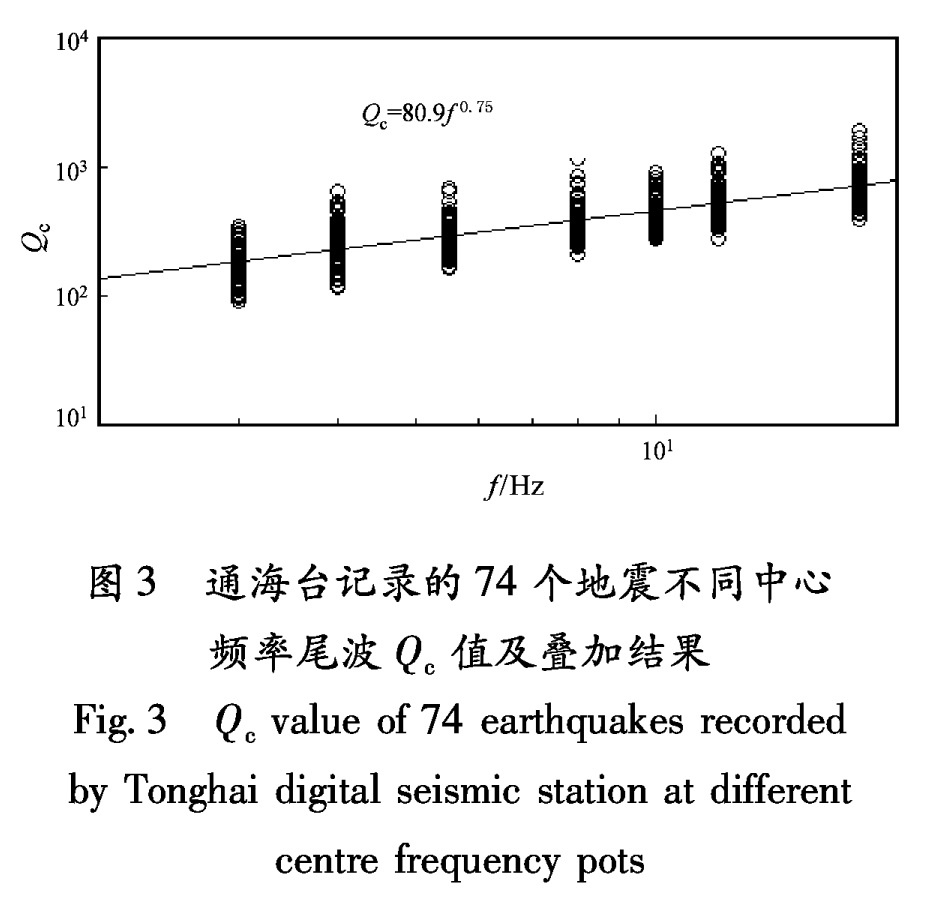
5.5 Hz、10.0 Hz 3个中心频率点的滤波波形。图2b给出了相应的各频率点上得到ln[A(f,t)*t]与t的曲线,以及用最小二乘法求出的Qc值结果; 图2b-1是用7个频率点(3.0 Hz、4.0 Hz、5.5 Hz、8.0 Hz、10.0 Hz、12.0 Hz、18.0 Hz)上的Qc值拟合得到Qc(f)的关系。把某个地震台记录到的所有地震不同中心频率都叠加到一张图上,即可以得到该台站记录到的所有地震的平均Qc值。以通海台为例,对该台记录到的74个中小地震不同中心频率点上的尾波Qc值,拟合得到Qc和η值,即得到Qc=80.9f 0.75关系(图3)。
图2 计算尾波Qc值的一个例子(a)原始波形及滤波后各中心频率的波形图;(b)地震尾波Qc值拟合结果示意图及各中心频率的ln[A(f,t)*t]与t的曲线
Fig.2 One example of Qc value calculation through Aki's model(a)Primary waveform and waveform filtered at different centre frequency pots; (b)The relationship between Qc value and frequency and the relationship between ln[A(f,t)*t] and t图3 通海台记录的74个地震不同中心频率尾波Qc值及叠加结果
Fig.3 Qc value of 74 earthquakes recorded by Tonghai digital seismic station at different centre frequency pots3 计算结果与分析
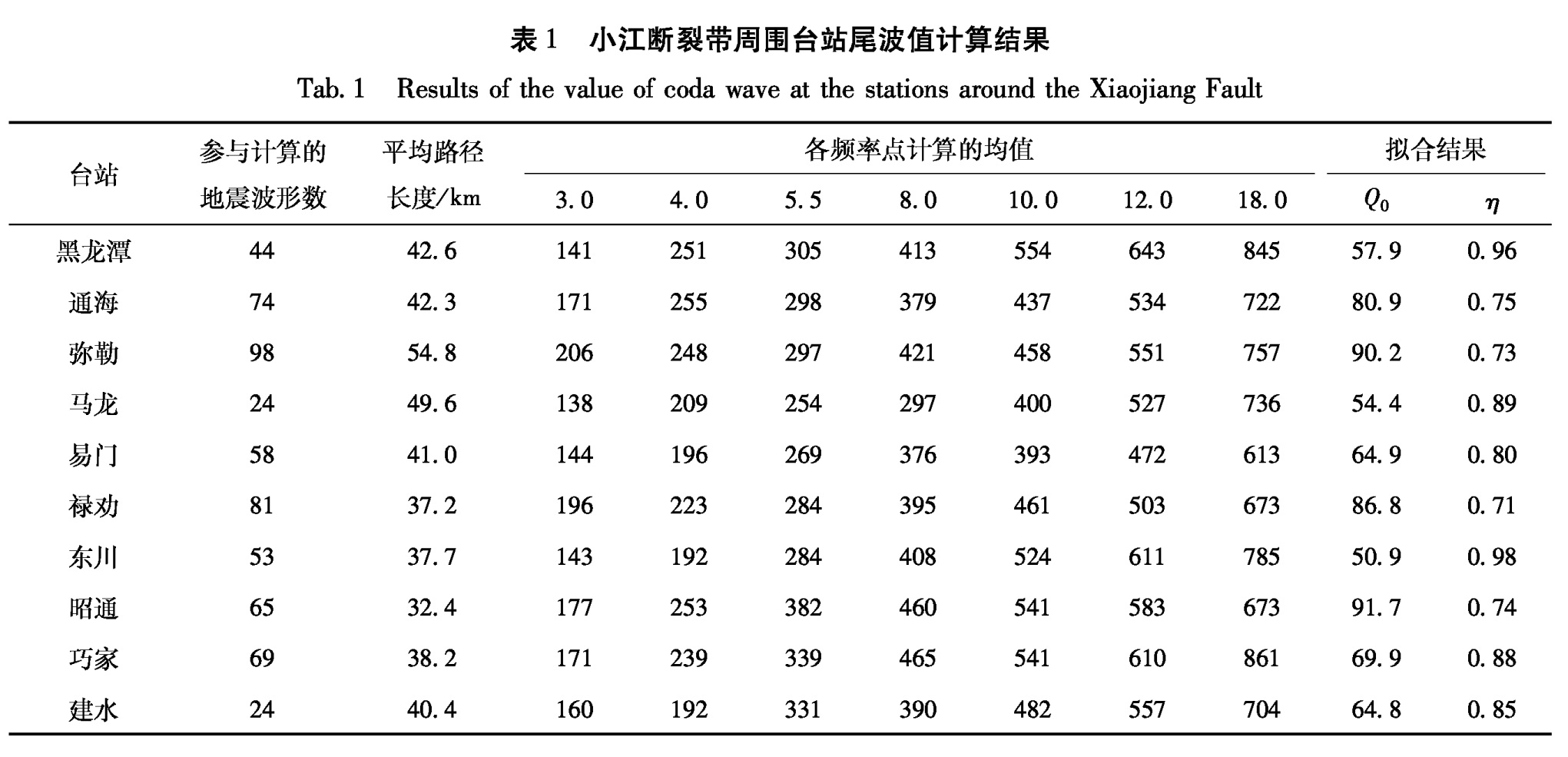
3.1 尾波Q0值空间分布特征按照上述方法和步骤,我们拟合得到了所选10个台站的Q0和η值(表1)。表1中还给出了用于计算的地震波形数和平均路径长度。用表1中10个台站在各频率点上的Qc值,最终得到平均拟合结果Qc(f)=75.4f 0.81,即得到研究区域的尾波Qc值与频率的关系。
根据已有的研究结果,姚安地震的尾波Qc=49f 0.95(李白基,秦嘉政,2004)、武定地震的尾波Qc=59f 0.95(秦嘉政等,2001)、宁洱余震序列的尾波Qc=53f 0.88(李琼等,2007)。小江断裂带中段的黑龙潭、东川、马龙三个台站尾波Q0值与上述值大致相当,表明这三个台站所处的区域构造活动水平与姚安、武定、宁洱等地相当,都是云南中强地震活动频繁的区域。而小江断裂带南段的弥勒、建水、通海,北段的昭通、巧家等台站的Q0值相对较高。根据Singn和Herrmann(1983)、Catherine和Woodgold(1990)、Hartzell等(1996)和秦嘉政等(2001)给出的国内外不同地区不同中心频率的地震波尾波衰减结果,小江断裂带南北段台站所处区域介质状态与构造地震活动相对较弱的美国中东部地区和中国河北昌黎地区明显不同,与美国加州斯通峡谷地区和云南武定、施甸、宁洱等构造地震活动频繁、强烈的地区也不尽相同,而是介于两者之间的一种活动状况,应该是一种中等构造活动的表现。
表1 小江断裂带周围台站尾波值计算结果
Tab.1 Results of the value of coda wave at the stations around the Xiaojiang FaultAki的理论是假定地球介质的Q值不变,事实上地球介质Q值是随深度变化的。黄才中和葛焕称(1995)用中国东部4省42个区域地震台周豪军等的记录以及发生于该区及邻近地区的51条地震记录研究了Q值与震中距的关系,结果表明Q值随震中距的增大而减小。本文给出了用于参与计算的地震与10个台站距离的平均路径长度(表1)。本文采用的是近震资料,震中距都在60 km范围内,每个台站的平均路径长度总体差别不大(32~55 km),从计算结果看,Q0值与平均路径的依赖关系不明显。这表明用近震地震波形资料计算区域地震尾波Q0值所得到的结果是可靠的,计算结果受所选地震震中分布影响较小。
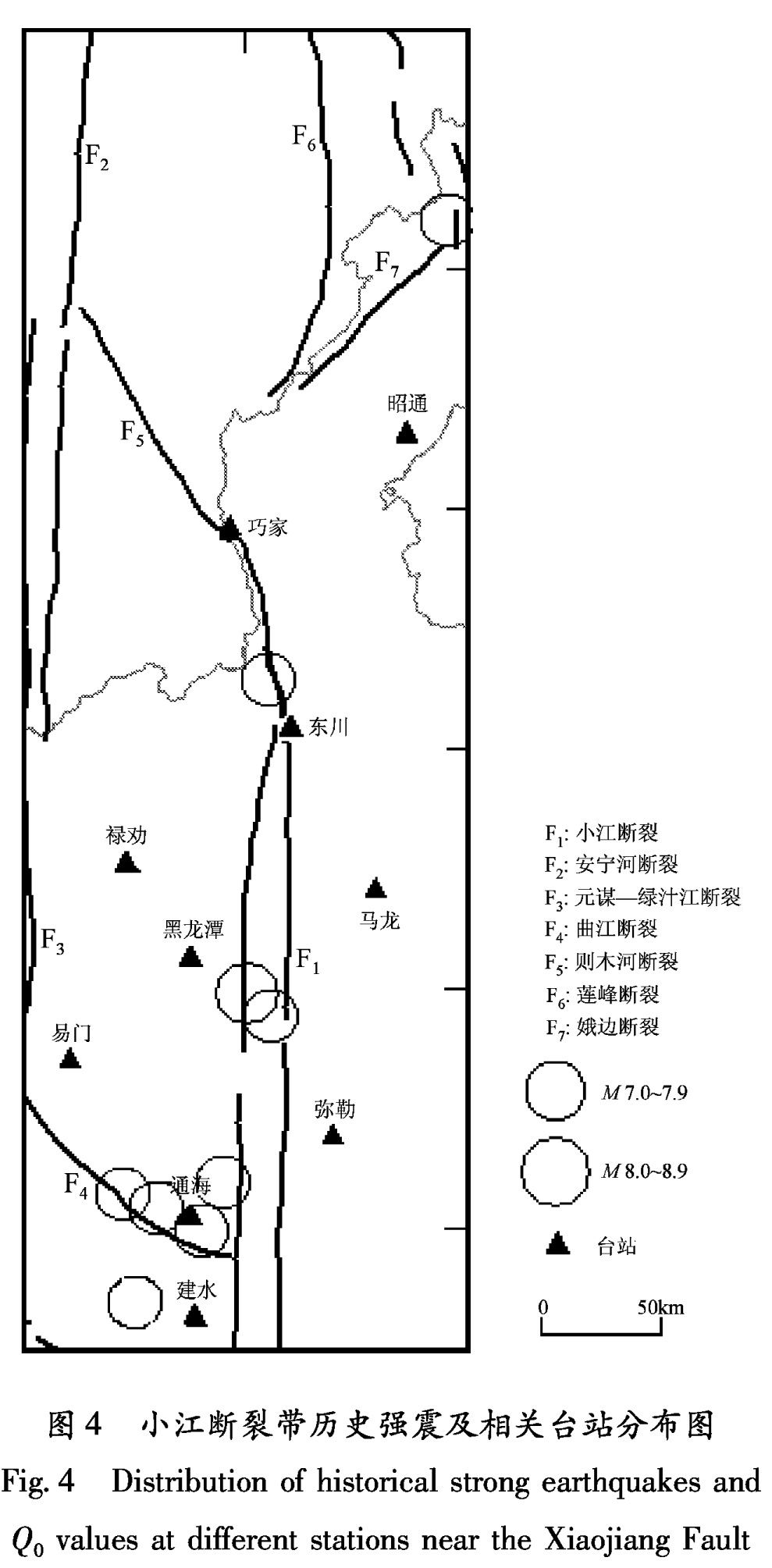
在所研究的10个台站中,Q0值最大的是昭通台,最小的是东川台。以10个台Q0值的1倍方差线为标准,高于1倍方差线的台站是昭通台和弥勒台; 低于1倍方差线的台站是马龙台和东川台; 黑龙潭台、易门台、禄劝台、巧家台和建水台Q0值在1倍方差线内。从空间区域分布来看,Q0值明显具有区域性分布特征,无论是7个中心滤波频率点的Q0值还是拟合所得的Q0值,位于小江断裂带中段台站的值都明显小于北段和南段的值。如黑龙潭、东川、马龙这三个台站附近60 km范围内的Qc和Q0值,总体上要比昭通、巧家、弥勒、易门、建水等台站低很多(图4、表1)。
下面笔者结合小江断裂带的区域构造、历史大地震分布等情况,对Q0值的空间分布特征予以初步解释。小江断裂带中段的历史强震活动要明显强于北段和南段。如图4所示,小江断裂带最大地震为1833年嵩明MS8.0地震,其次分别是1733年东川MS7.8、1970年峨山MS7.7和1500年宜良MS7.5地震,这4次地震中有3次位于小江断裂带的中段。秦嘉政(1992)年研究澜沧—耿马地震后尾波衰减特征发现,澜沧MS7.6地震余震区的地震尾波Qc值要明显低于耿马MS7.2地震余震区的地震尾及Qc值,分析认为这一原因可能是MS7.6地震造成的介质破碎程度远大于MS7.2地震,即低Qc值对应局部地区介质的非均匀性更强。历史强震使得震中附近介质破碎程度增加,导致介质稳定性变弱,从而使介质Qc值较低,故得到的距离历史大地震较近的小江断裂带中段台站的Qc和Q0值较低。北段的昭通台附近历史上仅有一次7级地震,且距离为100 km,远大于小震选取范围60 km,故该台表现出较高Qc值。而同样属于小江断裂带北段的巧家台,其拟合结果所得到的Q0
值明显小于昭通台。从图4来看,巧家台位于小江断裂带上,且距离1733年东川MS7.8地震震中较近,台站附近介质较为破碎,这可能是其Q0值小于昭通台的原因。图4 小江断裂带历史强震及相关台站分布图
Fig.4 Distribution of historical strong earthquakes and Q0 values at different stations near the Xiaojiang Fault钱晓东等(2006)认为地震波衰减对断层的破碎程度有明显的依赖关系:若地震波经过的路径上无深大破碎断裂带,地震波没有受到断裂带的强烈影响,因而表现出高Q0值特征; 若地震波经过断层破碎带,就受到强烈的散射和吸收,Q0值明显降低。同样位于相对稳定的华南地块的马龙台、弥勒台的尾波衰减参数却差别较大,对这两个台站参与计算的地震进行研究后发现,马龙台参与计算的地震记录共24条,其中位于小江断裂带以西的地震有10条。弥勒台参与计算的地震记录共98条,其中位于小江断裂带以西的地震仅21条,绝大多数地震波并没有经过较大断裂带,故Q0值明显比马龙台高。
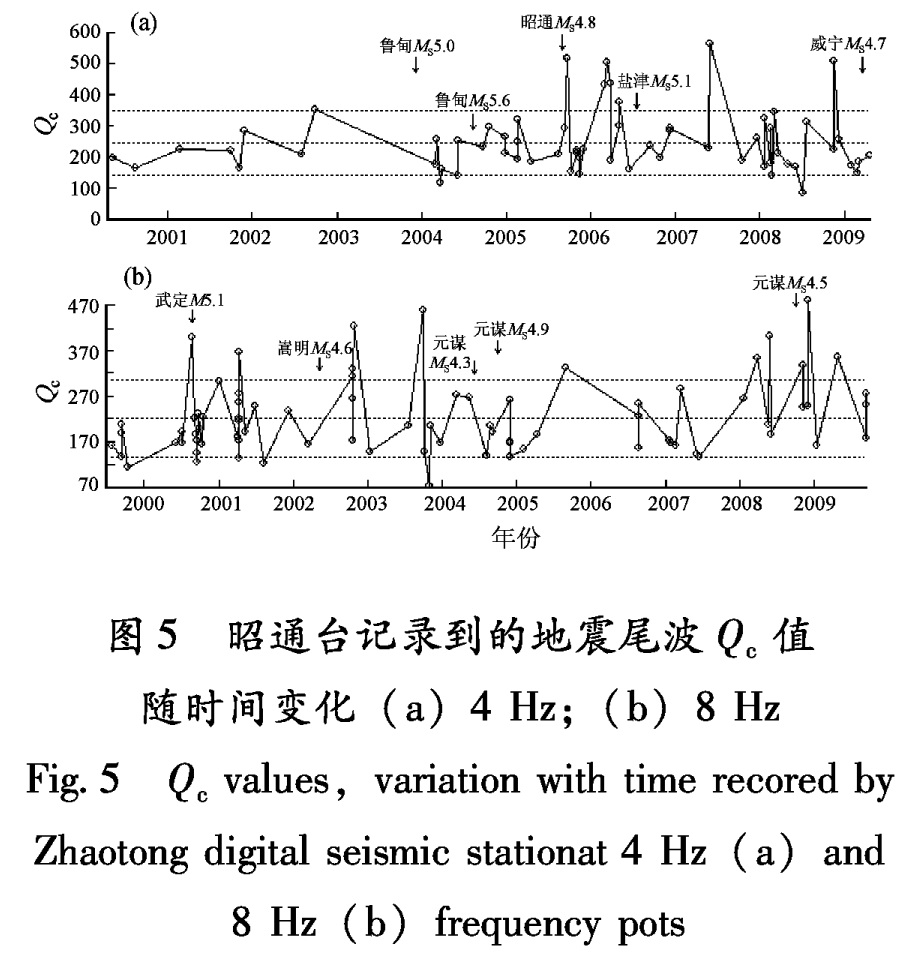
3.2 尾波Q0值时间变化特征及其应用在本研究区域和研究资料时段内,2003~2006年昭通台附近发生了多次5级地震,因此,笔者选择昭通台进行尾波Qc值时间变化与中强地震的关系研究。图5给出了在4 Hz、8 Hz两个频率点上昭通台尾波Qc值随时间的变化,两个小图中上、下两条虚线为1倍方差线。由图5可见,2000~2003年,其尾波Qc值变化相对平稳,波动幅度小(这一期间,该台记录到的符合计算条件的地震也较少); 2003年11月鲁甸MS5.1、5.0地震后,整个昭通台周边中强地震相对活跃,尾波Qc值上下波动起伏大。2003年11月鲁甸MS5.1、5.0地震和2004年鲁甸MS5.6地震前后,尾波Qc值未出现明显变化; 2006年8月盐津MS5.1地震前,在4 Hz频率点上尾波Qc值有一个高值过程,但在8 Hz频率点上未出现明显变化; 2009年3月威宁MS4.7地震前,在4 Hz、8 Hz两个频率点上均出现了一个单点高值异常。从本文的研究结果看,尾波Qc值时间变化与中强地震的关系还是不十分明确。部分尾波Qc值异常的出现可能是区域构造活动的表现,或小震活动引起Qc值波动,而不一定表现在中强地震活动上。
图5 昭通台记录到的地震尾波Qc值随时间变化(a)4 Hz;(b)8 Hz
Fig.5 Qc values,variation with time recored by Zhaotong digital seismic stationat 4 Hz(a)and 8 Hz(b)frequency pots4 结论与讨论
本文采用Aki单次散射模型,使用高斯滤波器,利用小江断裂带周边10个数字地震台记录到的地震波形资料进行了尾波Qc值计算,分别得到10个台站的尾波Q0和η值(即Qc(f)=Q0fη关系),并用10个台站的平均结果得到了小江断裂带及邻区尾波Qc值与频率的关系为Qc(f)=75.4f 0.81。研究发现,小江断裂带及邻区小江断裂带及邻区总体上属低Qc值区; 小江断裂带不同区域台站尾波Qc值差异较大,具有明显的空间分布特征:小江断裂带中段为低Qc值,明显低于北段和南段的Qc值。这种空间差异性可能与小江带不同区段上的构造活动、历史大震活动等因素有关。构造活动强烈,地震活动频繁地区一般为低Q值区,地震波衰减较快。一般认为,尾波Qc值是表征某个地区构造活动的指标之一,其变化反映了构造应力变化。因此,人们试图用区域性尾波Qc值随时间的变化特征来探索地震预测预报问题。目前主要有两种截然不同的认识:一种是主震前Qc值增大(高值异常),震后降低(Beroza et al,1995; 秦嘉政等,1995; Yoshihiro et al,2000; 王伟君,刘杰,2004; 马宏生等,2006); 另一种观点认为,某些情况下也能观测到Qc值相反的变化(啜永清等,2004)。造成上述结果的原因可能是不同作者在研究中采用的时间窗长、震中空间分布的差异及不同震源体等。Peng等(1968)针对上述可能存在的原因,采用不同时间窗长,且按照震中距大小进行分区,对美国加州Round Valley地区MS5.7地震前后尾波Qc值变化与前兆信息进行了详细研究,其结果可以简述为:主震震中附近的地区,震前Qc值高,震后下降; 距主震震中较远的地区,震前Qc值下降,震后变大。这一研究结果对用Qc值变化进行地震的时空预测有一定的指导意义。
通过对昭通台尾波Qc值随时间变化与其附近几次中强地震的关系研究,总体上可以看到,在中强地震相对平静时段,尾波Qc值变化较平稳; 在中强地震相对活跃时段,尾波Qc值上下波动起伏大。但其与具体某次地震的关系还不是十分明确。利用尾波Qc值的时间变化特征进行地震的预测研究,还需不断的积累震例资料。
- 啜永清,张淑亮,苏燕,等.2004.大同地震序列的尾波Qc值变化特征研究[J].地震,24(2):66-72.
- 黄才中,葛焕称.1995.中国东部的尾波衰减特征和Qc值估计[J].地震学报,17(2):196-202.
- 李白基,秦嘉政.2004.云南姚安地区的尾波衰减[J].地震学报,26(1):47-51.
- 李琼,秦嘉政,钱晓东.2007.2007年宁洱6.4级地震余震序列尾波Qc值研究[J].地震研究,30(4):337-343.
- 马宏生,刘杰,张国民,等.2006.云南地区尾波Qc值的分布特征及其初步解释[J].地震,26(3):37-43.
- 钱晓东,秦嘉政,李白基.2006.澜沧江流域水电工程地区的尾波衰减[J].地震研究,29(3):215-220.
- 秦嘉政,阚荣举.1986.用近震尾波估算昆明及其周围地区的Qc值及地震矩[J].地球物理学报,29(2):145-155.
- 秦嘉政,李白基,钱晓东,等.2001.云南武定地震余震近场尾波衰减的区域特征[J].地震学报,23(1):87-97.
- 秦嘉政,刘祖荫,龙晓帆.1995.滇西试验场两次中强地震前后尾波衰减的区域特征分析[J].中国地震,11(3):212-221.
- 秦嘉政.1992.澜沧—耿马地震后尾波衰减的区域特征[J].地震学报,14(1):71-82.
- 王伟君,刘杰.2004.1999年岫岩地震序列尾波Qc的变化过程[J].地震,24(4):37-44.
- Beroza G C,Cole A T,Ellsworth W L.1995.Stability of coda wave attenuation during the Loma Prieta,California earthquake sequence[J].JGR,100(B3):3977-3987.
- Catherine R D,Woodgold.1990.Estimation of Q in eastern Canada using coda waves[J].BSSA,88(2):411-429.
- Peng J Y,Aki K,Chouet B,et al.1968.Temporal change in coda Qc associated with the Round Valley,California,eathquake of November 23,1984[J].JGR,92(B5):3507-3526.
- Singn S,Herrmann R B.1983.Regionalization of crustal coda Q in the continental United states[J].JGR,88(B1):527-538.
- Hartzell S,Leeds A,Frankel A.1996.Site response for urban Los Angeles using aftershocks of the Northridge earthquake[J].BSSA,86(1B):168-192.
- Woodgold C D R.1990.Estimation of Q in eastern Canada using coda waves[J].BSSA,88:411-229.
- Xie J,Nuttli O W.1988.Interpretation of high-frequency coda at large distances:stochastic modeling and method of inversion[J].Geophysical J Int,95(3):579-595.
- Yoshihiro H,Nobuhiko H,Muneyoshi F,et al.2000.Temporal changes in coda Q-1cand b value due to the static stress changes associated with the 1995 Hyogo-ken Nanbu earthquke[J].JGR,105(B3):6141-6151.

![图2 计算尾波Qc值的一个例子(a)原始波形及滤波后各中心频率的波形图;(b)地震尾波Qc值拟合结果示意图及各中心频率的ln[A(f,t)*t]与t的曲线<br/>Fig.2 One example of Qc value calculation through Aki's model(a)Primary waveform and waveform filtered at different centre frequency pots; (b)The relationship between Qc value and frequency and the relationship between ln[A(f,t)*t] and t](2011年02期/pic55.jpg)