基金项目:国家自然科学基金(40930637)项目资助.
(College of Environmental Science & Engineering,Nankai University,Tianjin 300071,China)
the Haihe Fault; stochastic finite-fault model; near-field strong ground motion; peak acceleration
备注
基金项目:国家自然科学基金(40930637)项目资助.
通过构建横向均匀成层的地震断层模型,利用随机有限断层法,计算了海河断裂发生6.5级地震的地震动分布。计算结果克服了现行综合概率法计算结果不能体现近场效应的缺陷,并反映出断层上盘效应等特点,该结果可作为最大可信地震动应用于抗震设防变形验算,同时还可以作为评价综合概率法结果不确定性的一个参考,对海河断裂影响带的防灾减灾具有一定的借鉴价值。
The Haihe Fault is a major active fault in Tianjin.It is an important basis for the seismologists to determine the potential earthquake sources,and it plays a decisive role for people to select the aseismic design parameters.In this paper,we make a homogeneous layer of horizontal fault model to compute the effect of ground motion of a hypothetic M6.5 earthquake generated by the Haihe Fault using stochastic finite-fault method.The new method overcomes the shortcomings of the integrated probability method that can not reflect the near filed effect.And it reflects the upfault feature.The result from the new method can serve as the maximum credible ground motion to check seismic fortification deformation.The result which is useful for disaster reduction in this zone can also serve as a reference for integrated probability calculations.
引言
天津市地处华北平原东北部,是中国北方最大的沿海开放城市,同时也是我国北方的经济、海运与工业中心。21世纪以来,天津进入新的发展时期,经济社会的高速发展促进城市建筑由单一化向多样化转变,这些转变对工程场地地震安全评价提出了新的要求。海河断裂是穿越天津市区的一条主要活动断裂,由天津市西青区进入中心市区,沿海河经东丽区、津南区和塘沽区,从天津新港一带入海,延伸至渤海湾。该断裂是天津划分7级潜在震源区的主要依据,对潜源的范围、分布和震级上限等起决定性作用。因此,加强海河断裂的研究有助于更合理地进行抗震设防工作。
由于我国缺乏足够多的强震记录,目前使用的衰减关系主要依据美国西部震级小于7级、震中距为10~100 km的基岩强震记录,因此,设计地震动输入的研究还存在较多问题,如现行地震安全评价方法确定的反应谱的不合理性,常用衰减关系的近断层大震的适用性,近场大震震源破裂面的点源化近似,以及输入频率非平稳、结果不稳定等,都会对建筑物的抗震安全评价产生直接影响。笔者采用随机有限断层法对海河断裂进行模拟,综合考虑断层破裂的特征,同时通过子源间各子震的位置和上升时间等不同来体现震源的复杂性,更重要的是可不凭借衰减关系,直接给出近场强震引起的地震动,避免由于衰减关系的不适用而引起计算结果的不确定。
笔者以Boore(1983)改进的点源模型为基础,采用Brune(1970)的ω2震源谱,运用有限断层法对海河断裂的地震动进行随机模拟。该计算结果可作为最大可信地震动应用于抗震设防变形验算,同时也可作为评价综合概率法结果不确定性的一个参考,对海河断裂影响带的防灾减灾具有重要意义。
1 随机有限断层法
地震是由断层活动破裂产生的,点源模型是当震中距远远大于发震断层空间尺度时,将断层理想化为一个发生地震的“点”,然而当强震发生在近区域处(即近场的大尺度发震断层破裂),就必须考虑有限断层长度的影响。Beresnev和Atkinson(1997)提出模拟地震动的有限断层方法:假定地震破裂与一个有限的断层平面有关,该断层平面被划分为若干个矩形次断层(子源),根据断层的错动性质可确定破裂起始点(震源); 由震源点开始,当破裂传播到每个次断层的中心位置时,子源开始破裂,设定破裂的模式和破裂传播的速度,可得出子源破裂的时间顺序; 把每个次断层看作一个点源,根据子源与场址的几何关系,可以计算每个子源对场址的影响; 考虑每个子源的破裂传播到达的延时,分别叠加各子源的加速度时程,可得出有限断层破裂在场点处引起的地震动,避免了点源模型在近场区域将断层点源化处理的缺陷。
随机有限断层模型主要适用于拟合近场强地震动,很多研究已证明该方法具有可行性(Beresnev,Atkinson,1997)。另外,一些研究者多次模拟了有丰富强震资料的1994年北岭6.7级地震,与实际近场强震记录对比合成效果较好(王海云,2004; Beresnev,Atkinson,1997; 陶夏新,王国新,2003); 陶夏新和王国新(2003)还论证了这种随机方法在合成的时程中表达破裂的方向性效应和上盘效应,说明了其有效性。
1.1 随机有限断层法参数的确定(1)震源谱S(M0,f)
震源谱模型参数S(M0,f)采用Brune(1970)模式
S(M0,f)=(CM0)/(1+(f/(fa))2).(1)
式中,M0为地震矩; f为频率; fa为拐点频率; C为常数。
对于断层模型的震源尺寸,如果是已知地震可对现有记录反演得到,而预测未知地震时,只能根据经验公式估计,以下为Wehs和Coppersmith(1994)建立的模型
lgA=-3.49+0.91M,(2)
lgL=-2.44+0.59M.(3)
式中L(km)和A(km2)分别为断层长度和断层面积; M为矩震级。
(2)路径效应P(R,f)
简化的路径效应表示为几何扩散函数和滞弹性衰减函数的乘积
P(R,f)=Z(R)exp[-πfR/Q(f)CQ].(4)
式中,Q(f)为取决于某地区的岩石对波传导质量的品质因子,必须通过地震学监测来确定,一般岩石越软,该值越低; CQ为地震波速。几何扩散函数Z(R)是一个分段连续函数
Z(R)={(R0)/R R≤R1
Z(R1)((R1)/R)P1 R1≤R≤R2
Z(Rn)((Rn)/R)Pn Rn≤R.(5)
其中R取距断裂表面的最近距离,而不是震源距。分段函数中的参数分别根据Atkinson和Boore(1995)估计美国东北部地震动时取的参数值:R0=1、R1=70、p1=0.0、R2=130、p2=0.5。
(3)场地效应G(f)
场地效应一般可以表示为放大项A(f)和衰减项D(f)的乘积,即
G(f)=A(f)×D(f).(6)
其中,放大函数A(f)可用震源和地表之间的波阻抗比的平方根求得,求解过程比较复杂,这里不再详述,实际应用时可根据场地的钻孔资料确定。衰减项D(f)考虑地震动中与路径无关的高频损失,Boore(1983)建议采用简单的滤波器来表示高频地震动的衰减。笔者所用滤波器为κ滤波器(Anderson,Hough,1984)为
D(f)=exp(-πκf),(7)
式中,κ为kappa参数,Atkinson(1996)建立了kappa参数与矩震级之间的经验关系式
κ=0.0106MW-0.012.(8)
(4)子震震源参数的确定
王国新和史家平(2008)根据相关研究结果,结合子源合成地震动方面的经验,经反复试验和摸索,认为发生4~8级地震时,均有一特定的子源几何尺度可以使拟合结果最为理想,在大震震级(M)和破裂长度(L)已知的情况下,与子震震级(MZ)相应的子源平均破裂长度(ΔL)可以表示为
lg(ΔL)=lg(L)-0.5(M-MZ).(9)
因此,选择能使子源基本可以视为点源的子震震级,然后可根据式(9)确定子源几何尺度的大小。目前,一般均认为MZ的上限以5~5.5级为宜(陶夏新,王国新,2003)。
控制子源能量之和等于地震总能量,即所有发生子震地震矩之和应与大震地震矩一致。求得大震地震矩和子震地震矩,即可得到整个断层面发生子震的个数。由于破裂不均匀,计算可能使一个子源中分配到多个子震。
利用有限断层模型对地震的发震断层进行划分,确定子源地震矩
Me=Δσ*A*ΔL,(10)
再根据大震总地震矩,确定子震个数
Ne=(M0)/(MZ).(11)
每个子源都可作为一个点源处理:结合Brune(1970)的ω2震源谱,将各子源地震动过程作为有限持时、有限带宽的白噪声直接合成地震加速度时程; 设定断层的破裂方式和传播速度后就可计算出全部子源破裂的时间顺序,根据场地和每个子源的空间关系,计算各子源对场址的影响,并考虑每个子源的破裂传播到达的延时,分别叠加各子源的加速度时程,就得到有限断层在场点处引起的地震动:
a(t)=∑NLi=1∑NWj=1aij(t+Δtij).(12)
式中,NL和NW分别是沿断层长度和宽度方向的子断层数,NL×NW=N为子源总数; Δtij包括破裂传播到第ij个子源引起的时间滞后和从第ij个子源至场点间由于传播距离的不同引起的时间滞后; aij(t)是第ij个子源引起的观测点地震动。
2 海河断裂计算模型
2.1 海河断裂概况海河断裂属于张家口—渤海断裂带,张家口—渤海断裂带又称张家口—蓬莱断裂带,由近20条NW—NWW向断裂组成,这些断裂一般长40~60 km,倾角较大,该断裂带西起张家口以西,沿SE方向经怀来、南口、顺义、三河和天津等地,穿过渤海一直延伸到蓬莱附近海域,总体呈NW向展布,全长700多千米,总体表现为左旋走滑性质。海河断裂位于张家口—渤海断裂带的南侧,呈NW—NWW方向,自河北省固安附近,沿SE方向穿过天津市西青区及中心市区,沿海河经东丽区、津南区和塘沽区,从天津新港一带入海,一直延伸到渤海湾西部,在天津地区探明其长度为70余千米。该断裂倾向SSW,倾角70°左右,主要表现为左旋走滑性质,兼有一定的垂直向拉张滑动。
2.2 模型建立根据式(2)和式(3)计算得到断层尺寸为25 km×10 km,按照上述方法,本文将整个断层面划分为10个5 km×5 km的子源,每个子源的地震矩按照式(10)计算
Me=(Δσ)*A*(ΔL)=5.75×1017.(13)
因此发生子震的总个数
Ni=(7.07×1018)/(5.75×1017)≈12.(14)
计算结果表明,总共有10个子源,发生子震的次数为12。为了体现震源内介质的不均匀性,假定整个断层面错动量是不相等的,也就是破裂位错非均匀分布,因此设定震源就近的2个子源要发生2次子震,这2个子源所释放出的能量较其它子源高。个别子源发生多于一次地震的情况,体现了震源内介质的不均匀性。
3 计算结果及其分析
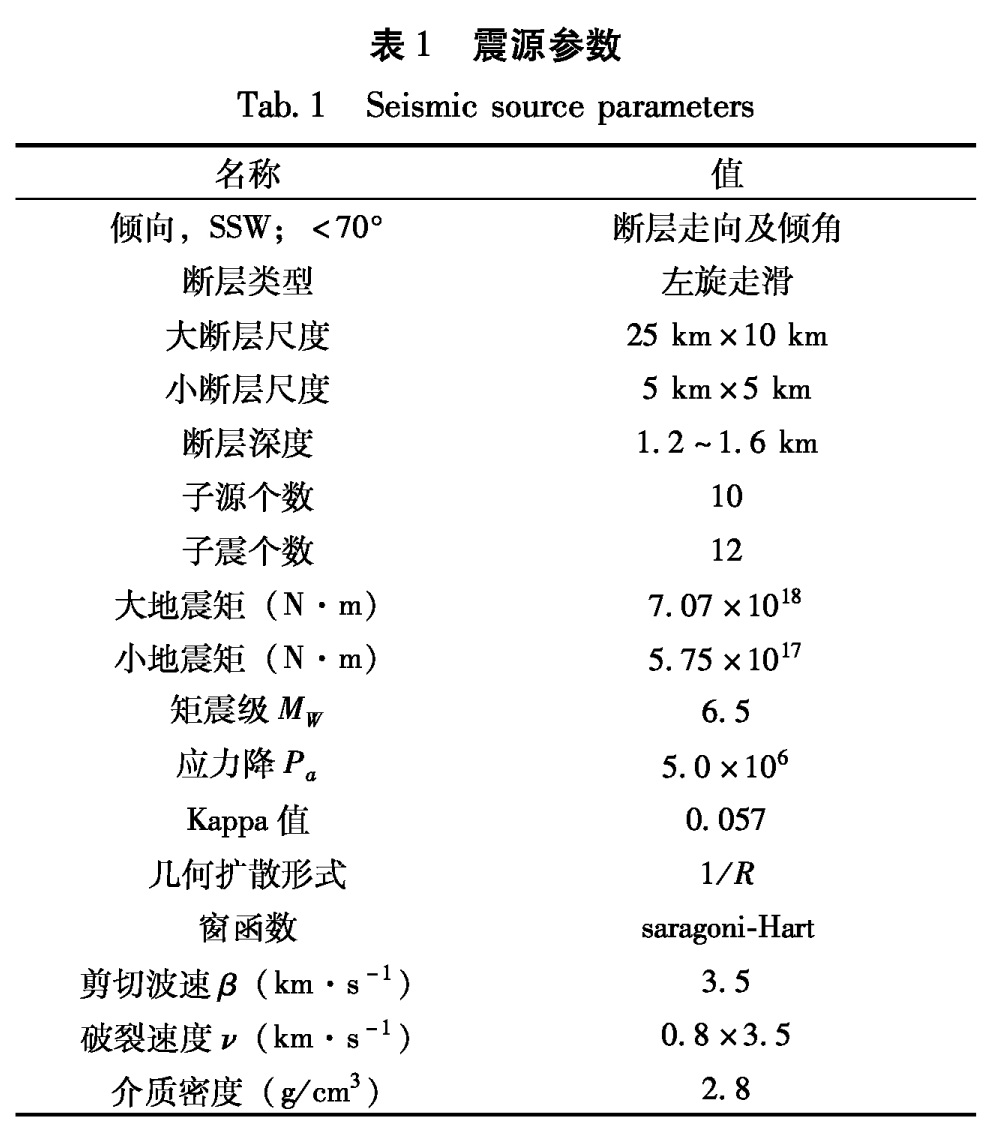
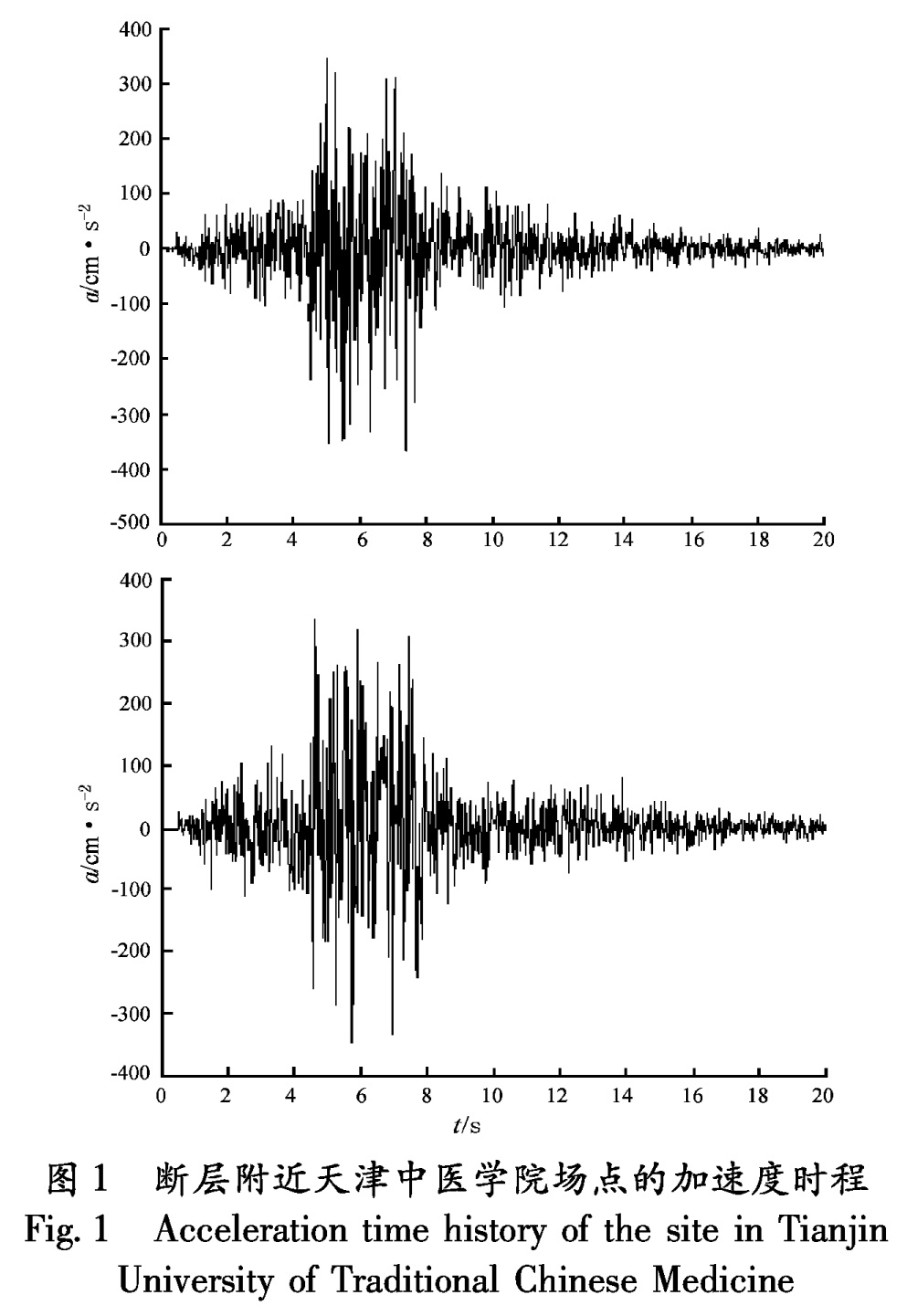
为了对海河断裂地区的地震动情况做出总体预测,笔者采用随机有限断层法对近断层范围内加速度时程按照网格划分的方式进行逐点合成计算(史家平,2008),并根据计算结果绘制了加速度等值线图。计算场点取在断层附近,范围是39.03°~39.17°N,117.13°~117.27°E,结合表1和表2的参数进行合成:
(1)取断层破裂面附近天津中医学院的场点(坐标位置:39.01°N,117.15°E)随机合成了两条加速度时程(图1),从图中可以看出两条加速度时程的峰值分别为:362 cm/s2,351 cm/s2。
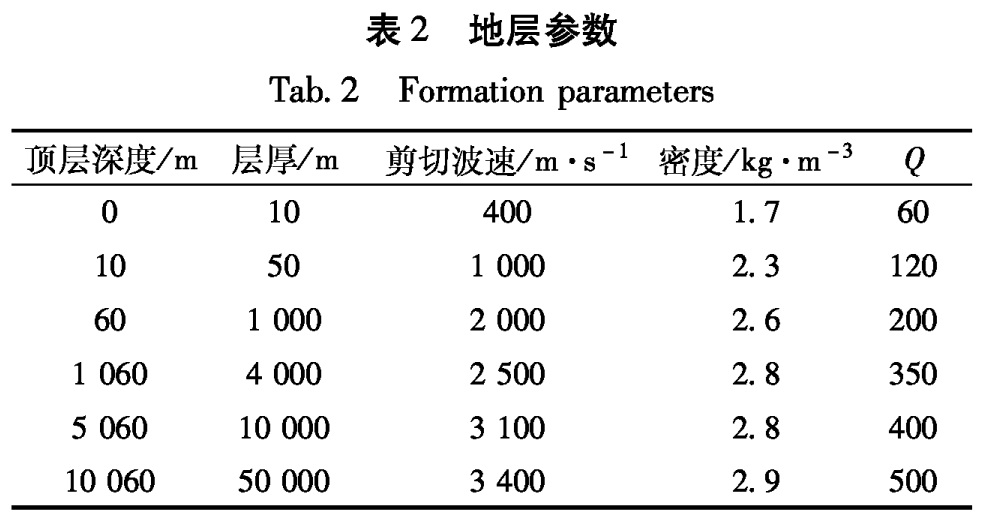
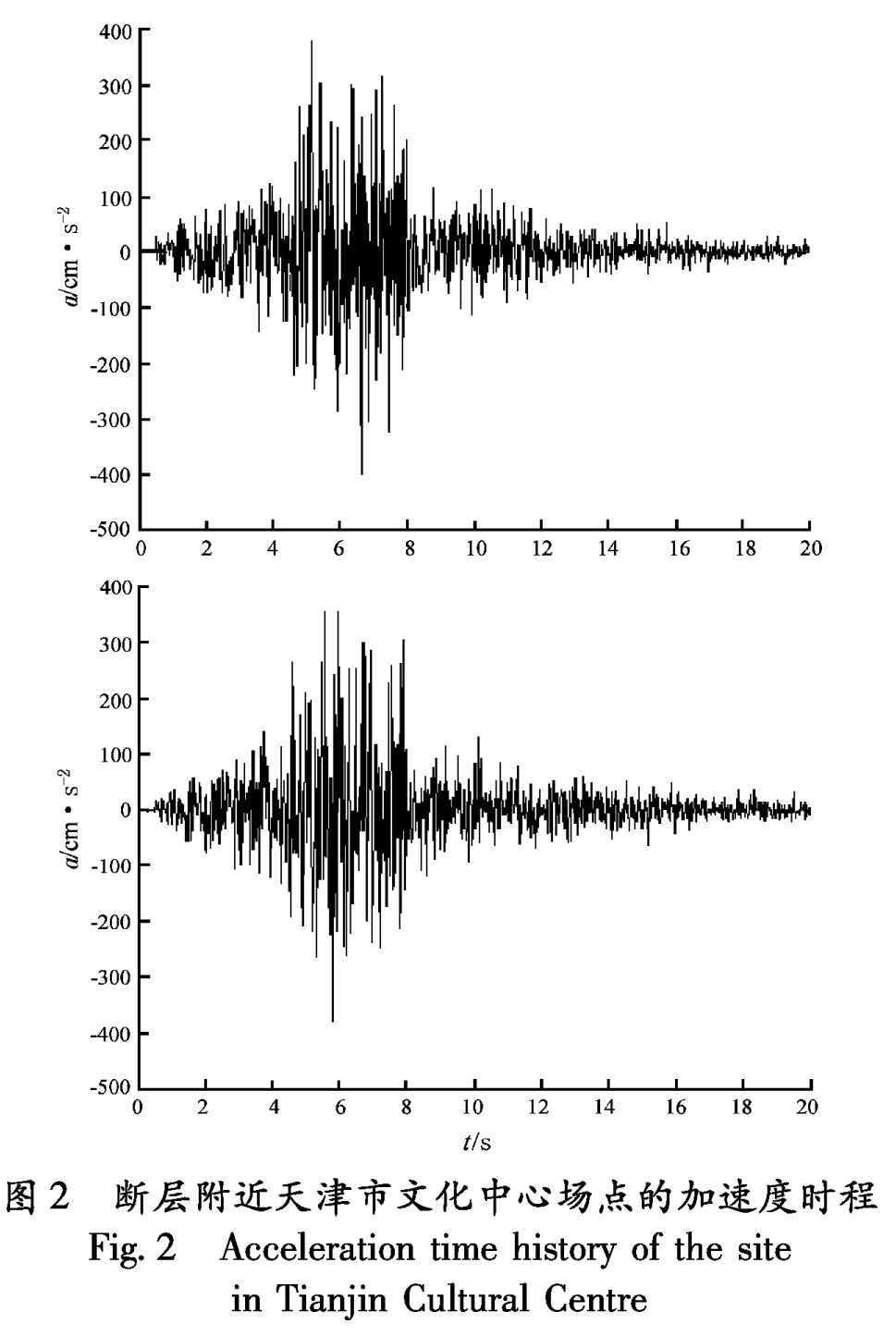
(2)取天津文化中心的场点(坐标位置:39.08°N,117.22°E)随机合成两条加速度时程(图2),从图2中可以得出两条加速度时程的峰值分别为:402 cm/s2,395 cm/s2。
将以上两个场点的峰值加速度分别和《中医临床研究基地中国针灸中心大厦项目场地地震安全性评价报告》 赵瑞斌,易立新.2009.中医临床研究基地中国针灸中心大厦项目场地安全性评价报告.、《天津市文化中心建设项目场地地震安全性评价报告》 赵瑞斌,易立新.2010.天津市文化中心建设项目场地震安全性评价报告.评价结果相比较,计算结果基本一致。图1 断层附近天津中医学院场点的加速度时程
Fig.1 Acceleration time history of the site in Tianjin University of Traditional Chinese Medicine(3)经度和纬度都按2'递增,计算39.03°~39.17°N,117.13°~117.27°E范围内各点的加速度时程画出这些点的等值线(图3)。
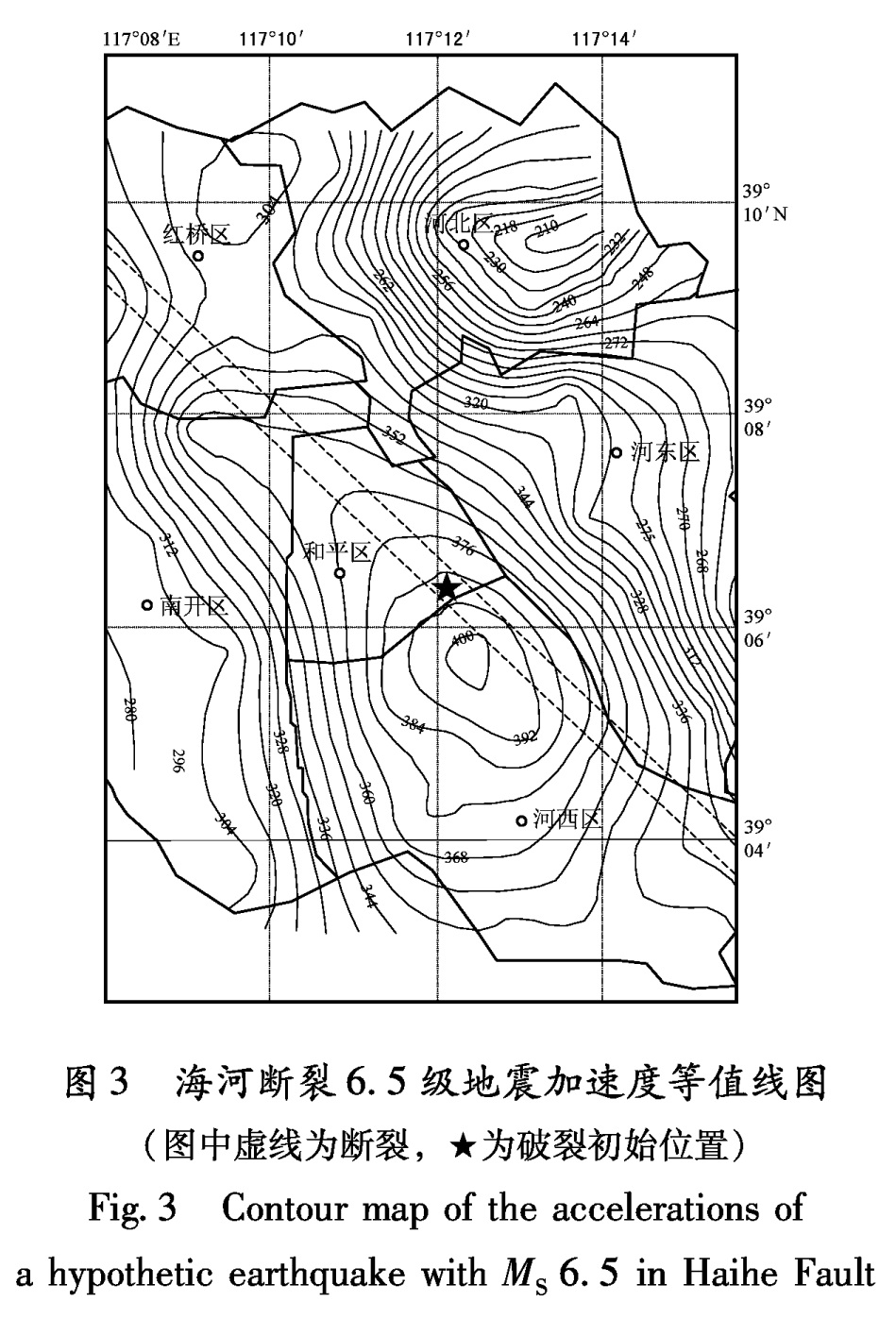
图3 海河断裂6.5级地震加速度等值线图(图中虚线为断裂,★为破裂初始位置)
Fig.3 Contour map of the accelerations of a hypothetic earthquake with MS 6.5 in Haihe Fault4 结论与讨论
通过计算海河断裂6.5级地震可以看出:计算范围内加速度达到400 cm/s2以上,大致在和平区和河西区的交汇处,最大加速度影响圈也大部分位于此范围内,平均加速度在360 cm/s2和380 cm/s2之间。在距离断层较远的河北区地震动为目标区内最小,平均加速度在240 cm/s2左右。
通过计算还可以得出以下结论。
(1)峰值加速度不一定在断层上,通常出现在断层附近。
(2)从整个加速度分布图形来看,形成以断层破裂面为中心,向四周随距离增大逐渐衰减的趋势; 且沿破裂传播方向,随着与破裂点距离增大,加速度峰值出现的时间向后推移。
(3)沿着断层方向,地震动峰值加速度明显大于其他方向; 而且断层上盘地震峰值加速度峰值大于同等情况下的下盘峰值加速度,体现了断层的上盘效应。
笔者运用随机有限断层法研究了海河断裂发震时产生的地震动特征,该方法原理比较简单,但定量考虑了断层类型因素和具体特征(各子源的几何位置),同时震级、震源距、场地条件、断层与场地的相对方位等因素均得到了合理考虑,拟合的结果基本能满足实际工作的需要,适用于确定场地地质条件和重大工程选址以及进行小范围的危险性分析和灾害评价。
- 史家平.2008.地震动合成方法比较与研究[D].大连:大连理工大学.
- 陶夏新,王国新.2003.近场强地震动模拟中对破裂的方向性效应和上盘效应的表达[J].地震学报,25(2):191-198.
- 王国新,史家平.2008.近场强地震动合成方法研究及地震动模拟[J].东北地震研究,24(2):4-10.
- 王海云.2004.近场强地震动预测的有限断层震源模型[D].哈尔滨:中国地震局工程力学研究所.
- Anderson,J G,Hough S E.1984.A model for the shape of the fourier amplitude spectrums of acceleration at high frequencies [J].BSSA,74(5):1969-1993.
- Atkinson G M,Boore D M.1995.Ground motion relations for eastern north America[J].BSSA,85(1):17-30.
- Atkinson G M.1996.The High-frequency shape of the souree spectrum for earthquakes in eastern and western Canada[J].BSSA,86(1A),106-112.
- Beresnev I A,Atkinson G.1997.Modeling finite—fault radiation from the ω2 spectrum[J].BSSA,87(1):67-84.
- Boore D M.1983.Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra[J].BSSA,73(6):1865-1983.
- Boore D M.2003.Simulation of ground motion using the stochastic method[J].Pure appl.Geophys.160(3-4):639-661.
- Brune J N.1970.Tectonic stress and the spectra of seismic shear waves from earthquakes[J].J.Geophys.Res.,75(26):4997-5009.
- Wehs D,Coppersmith K.1994.New empirical relationships among magnitude,rupture length,rupture width,rupture area,and surface displacement[J].BSSA,84(4):974-1002.