基金项目:科技部社会公益研究专项“石窟文物抗震防护技术对策研究(2002DIB20062)”资助.
(1.中国地震局地球物理研究所,北京 100081; 2.中国地震局地震预测研究所 兰州科技创新基地,兰州 730000; 3.中国建筑科学研究院,北京 100013)
(1.Geophysics Institute,CEA,Beijing 100081,China)(2.Lanzhou Base of Institute of Earthquake Prediction,CEA,Lanzhou 730000,Gansu,China)(3.China Academy of Building Research,Beijing 100013,China)
ground motion; country rock; dynamic failure; Longmen Grottoes
备注
基金项目:科技部社会公益研究专项“石窟文物抗震防护技术对策研究(2002DIB20062)”资助.
以洛阳龙门石窟为研究对象,阐述了地震荷载下洞窟围岩损伤的影响因素; 采用动力有限元法,从地震动的不同工程特性、不同输入方向等方面入手,分析研究了不同地震作用下洞窟围岩的位移、速度和应力动态变化特征,并指出了围岩内振动位移、速度最大值以及应力集中出现的地方,对有无裂隙两种情况下围岩的位移、速度和应力值进行了对比。最后,根据岩体强度和莫尔—库仑破裂准则,分析了围岩在不同地震作用下可能出现的拉性、压性以及剪性破坏,为石窟文物地震安全评估及防灾对策研究提供了依据。
We list the main influencing factors causing the failure of the country rock of the Longmen Grottoes in Luoyang City,Henan Province.Using finite element method,and aiming at the engineering characteristics,input directions,etc of the ground motion,we study the dynamic displacement,velocity,and stress variation of the country rock under different seismic loads and determine the locations where the maximum displacement,maximum velocity and stress concentration appear.Then,we compare the displacement,velocity,and stress of the country rock which has fractures with the ones of the courtry ROCRwhich has no fractures.On the basis of the Mohr-Coulomb Failure Criterion,we study the possibility of failure of the country rock,which serves as a reference for the assessment of seismic stability and the protection of culture relics of the Grottoes.
引言
龙门石窟位于河南省洛阳市城南13 km的伊河东西两岸的石质陡崖中,携同敦煌莫高窟、大同云冈石窟并称中国三大著名佛教石窟,均以其规模之大、文物价值之高而闻名于世,最早被列为世界文化遗产。多年来,这些宝贵的文化遗产受到了不同振动形式的影响,出现过窟顶坍塌、崖面崩塌与滚石以及岩体裂缝等灾害现象。一些学者在相关方面进行过比较详细的研究(付长华,石玉成,2004; 李海波,吴绵拔,1995; 李海波等,2003; 牟会宠等,2000; 秋仁东等,2009; 石玉成等,2002,2006; 王现国等,2006)。地震由于突发性、成灾的巨大性等特点,成为影响石窟文物稳定性的重要因素。经统计(国家地震局震害防御司,1995,1999; 中国地震台网中心,2010),自公元前23世纪到现在,龙门石窟外围180 km范围内共记录到3级以上地震70多次(图1),其中3~3.9级地震13次,4~4.9级地震17次,5~5.9级地震29次,6~6.9级地震10次,7级和8级地震各一次。在洛阳市就分别发生过4级和5级地震。根据现行的全国地震区划结果,洛阳市50年超越概率10%的地震峰值加速度为0.1 g(胡聿贤等,2001)。因此,本文旨在研究龙门石窟的围岩在地震荷载下的变形破坏特征,以期为该石窟文物的抗震防护提供借鉴。
1 地震荷载下龙门石窟围岩动态损伤的影响因素
1.1 环境工程地质条件龙门石窟开挖在伊河两岸的高陡边坡内,岩性为寒武纪石灰岩。边坡为折线型,石窟密集区段上部坡角约70°~75°,下部坡角约65°,坡高约55 m。边坡内发育有4组构造节理:J1:120°∠78°; J2:180°∠70°~80°; J3:90°~110°∠75°; J4:220°∠75°~85°。边坡走向近南北,倾向东,因而其稳定性主要受走向为180°左右的节理面组控制 曹美华,潘别桐.1988.龙门石窟立壁边坡岩体卸荷带形成的有限元模拟分析.。根据石窟文物区岩体波动测试的结果及有关的文献资料(李海波,吴绵拔,1995; 李海波等,2003; 王现国等,2006),得到了岩体力学参数(表1)。
工程地质岩组 弹性模量E/MPa 泊松比γ 密度ρ/g·cm-3 抗压强度/MPa 抗拉强度/MPa 内聚力C/MPa 内磨擦角Ф灰岩 2.4×104 0.25 2.65 123 5.85 53 29°
1.2 工程因素龙门洞窟群系在不同时代开挖,在崖面上紧密分布。洞室长一般3~8 m,少数达15~20 m,宽高约3~8 m,部分小洞仅1~1.5 m见方,拱顶多见穹窿形。洞室间隔墙及顶、底板岩层一般较薄,其厚度仅为0.5~2 m。
1.3 地震因素在各种地震动参数中,只考虑具有不同工程意义的地震动峰值加速度(PGA)、频谱特征周期(Tg)和持时(Dura)三个方面的因素。计算过程中,为了满足研究需要,选用了4条具有不同工程意义的地震动时程,特征周期分别考虑0.25 s、0.4 s及0.55 s共3种情况,总的持续时间为16 s或28 s,以充分反映未来可能的地震动特点(图2)。
输入峰值加速度考虑0.1 g和0.2 g两种情况,以便进行对比分析。2 有限元分析原理和方法
2.1 分析原理根据经典弹性理论的假定,将莫高窟围岩视为理想的线弹性体,在具体的计算过程中引入运动平衡方程
Mu··+Cu·+Ku=-Mx··g.(1)
式中,M为体系的总质量矩阵; C为体系的总阻尼矩阵; K为体系的总刚度矩阵; u··、u·和u分别为体系的节点加速度向量、速度向量和位移向量; x··g为施加到结构上的地震动加速度向量。运动平衡方程的求解采用Newmark隐式时间积分法。
体系采用Rayleigh阻尼,即C=αM+βK,其中α为质量阻尼系数,β为刚度阻尼系数。
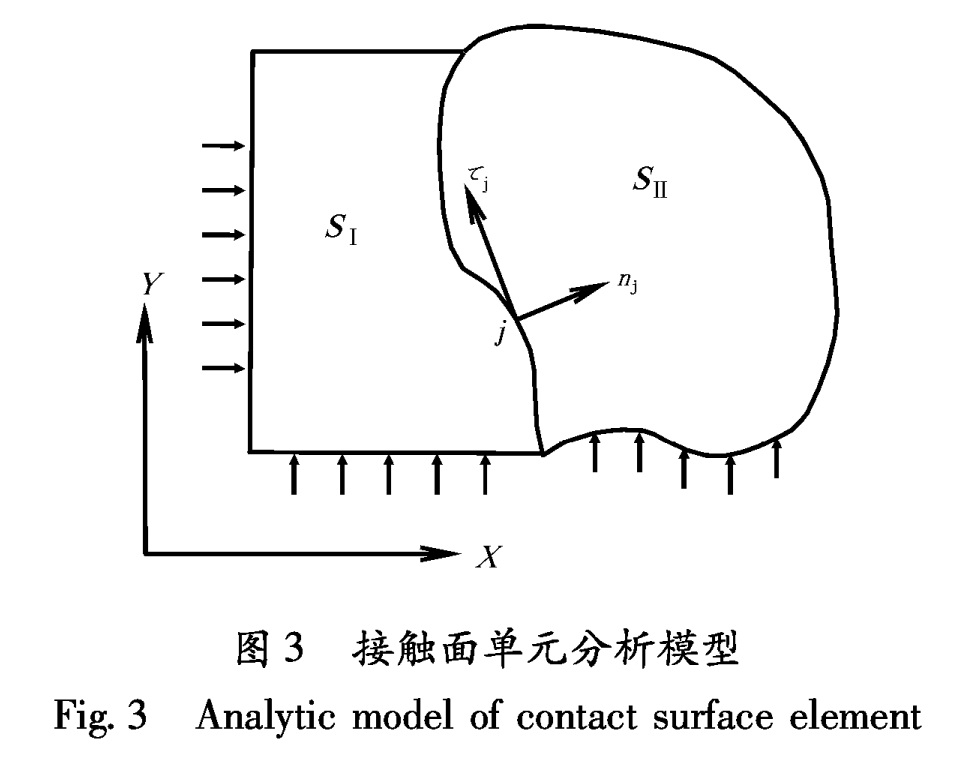
2.2 裂隙周围的岩体动接触问题将裂隙考虑成接触边界,两边的岩体视为在边界上相互接触的两个物体SⅠ,SⅡ(图3)。对于其中任一个接触点j,取SⅠ物体上该点法线方向作为n方向,然后逆时针方向旋转90°,作为其τ方向,以(nj,τj)组成局部坐标系。设SI,SII上接触点对法向接触力为Fnij(i= I,II; j=1,2,…,k; k为接触点对数),切向接触力为Fτij,相应的法向位移和切向位移分别为uij和vij。在地震动作用下,接触面可以保持连续,也可以相对滑动甚至分离,各种接触状态下接触面的连接条件可以简述如下:
(1)连续状态
FnIi+FnIIj=0; FτIj+FτIIj=0,
uIj=uIIj,vIj=vIIj.(2)
(2)相对滑动状态
FnIi+FnIIj=0; FτIj+FτIIj=0,
uIj=uIIj,FτIj=±μFnIj.(3)
(3)分离状态
FnIj=FnIIj=FτIj=FτIIj=0.(4)
接触磨擦问题需经多次迭代才能获得正确解,计算时,首先假设单元处于某种接触状态,按照假定的状态,分别计算等效单元刚度矩阵和等效荷载向量。解有限元方程后,得到一组试验解。将试验解进行接触状态检查,看其是否与原假设状态相同。若相同,说明原假设接触状态正确,相应的解即为正确解,计算结束; 若不同,则选取试验解为新的假设状态,并修改荷载向量,进行新的一轮迭代,直至收敛。
2.3 计算模型实体模型宽70 m,高70 m,右边与山体相连,左边取地表至地下深度15 m处。模型中分布有上下两个洞窟,顶部发育有与崖面平行的卸荷裂隙。有限元计算模型见图4,裂隙模拟成接触单元,假定模型左右两侧受水平方向位移限制,底边受水平与垂直方向位移限制,崖面为自由边界,计算时分别以不同工程特性和不同激振方向的地震动加速度时程作为输入。
利用现有的工程加固技术(如裂隙灌浆、锚杆加固等),可以很好地整合裂隙周围的岩体,有效地提高其力学性能(何开明等,2003; 秋仁东,2006)。因此,不妨假设已通过上述某种方法消除了裂隙的存在,重新生成有限元模型,并计算岩体的地震反应,以探讨工程加固技术对岩体地震稳定性的影响与作用。
3 围岩变形破坏机制研究与分析
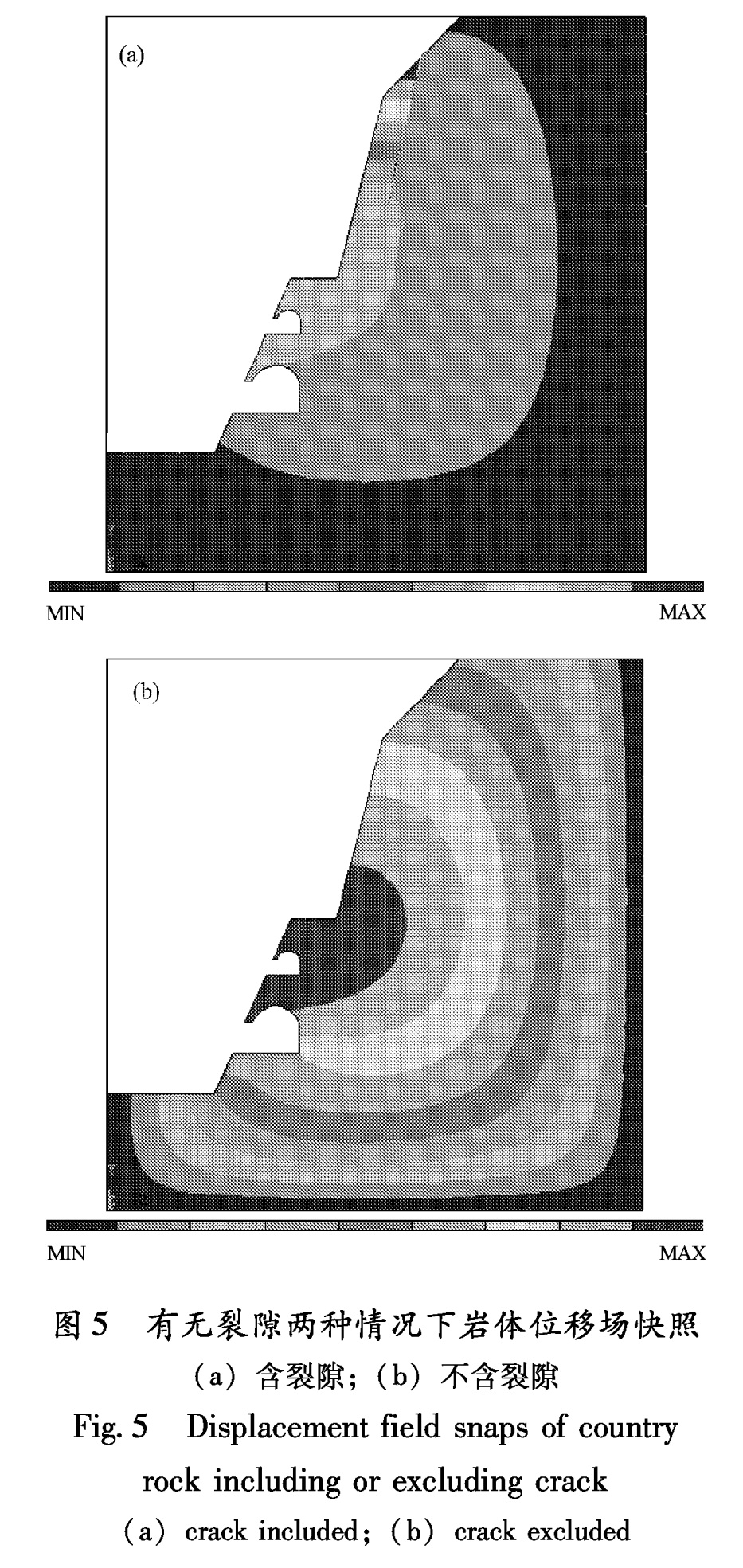
3.1 围岩振动位移分析地震为一个随机振动过程,引起的岩体的位移响应也是随时变化的。但其一般形态特征可见图5。由于裂隙的存在,洞窟围岩的最大振动位移分布于崖顶裂隙处外侧,沿裂隙处张开,顺坡面向下位移逐渐减小; 其次是洞窟所在处的突出部位,约束边界处位移最小。当没有裂隙时,岩体振动位移的最大值出现在洞窟所在处的突出部位,并以该部位为中心近似呈辐射状向四周减小。
(1)不同PGA对位移大小的影响
通过对比PGA分别为0.1 g和0.2 g两种情况下岩体的振动位移曲线,可以看出地震动加速度大小变化显著地改变了岩体在地震荷载下的位移
反应。随着地震动峰值加速度的增大,围岩的振动位移增大(图6)。图5 有无裂隙两种情况下岩体位移场快照
(a)含裂隙;(b)不含裂隙
Fig.5 Displacement field snaps of country rock including or excluding crack(a)crack included;(b)crack excluded(2)不同持时对结构位移大小的影响
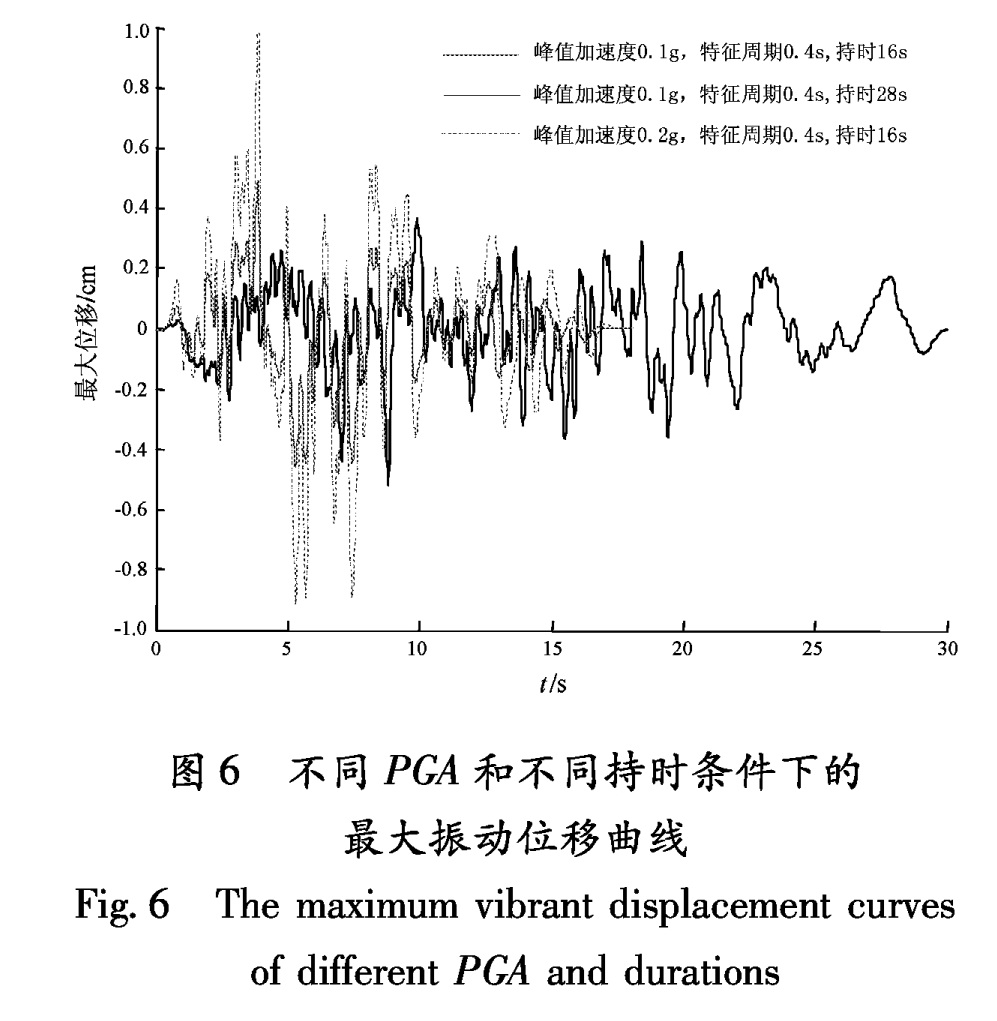
如图6所示,在相同的加速度峰值(0.1 g)和相同特征周期(0.4 s)、但不同的持时(分别为16 s和28 s)的地震荷载下,得到的位移最大值均为0.5 cm左右,说明持时对围岩在地震作用下的位移反应基本没有影响。
(3)不同特征周期对振动位移大小的影响
根据图7可知,在相同峰值和持时作用下(PGA=0.1 g,持时为28 s),特征周期增大,围岩的位移响应随之增大。说明随着长周期地震动成分的增加,会引起岩体的位移反应加大。
图6 不同PGA和不同持时条件下的最大振动位移曲线
Fig.6 The maximum vibrant displacement curves of different PGA and durations(4)考虑竖向地震动对振动位移大小的影响图7 不同特征周期条件下的最大振动位移曲线
Fig.7 The maximum vibrant displacement curves of different characteristic periods根据现有对地震地面运动的认识,竖向地震动的峰值加速度可以达到水平向峰值加速度的1/2~2/3,因此对只有水平地震动输入,以及水平和竖向地震动同时输入两种情况分别进行了计算。根据建筑抗震设计规范(2001),竖向PGA大小设定为水平向PGA的0.65倍。计算结果见图8,由图8可以看出,相比仅有水平地震动输入,当同时考虑竖向地震动时,最大振动位移高出了约0.1 cm(20%)。
(5)有无裂隙存在对振动位移大小的影响
从图8可以看出,在同样的地震动条件下(PGA=0.1 g,Tg=0.4 s,Dura=16 s,水平输
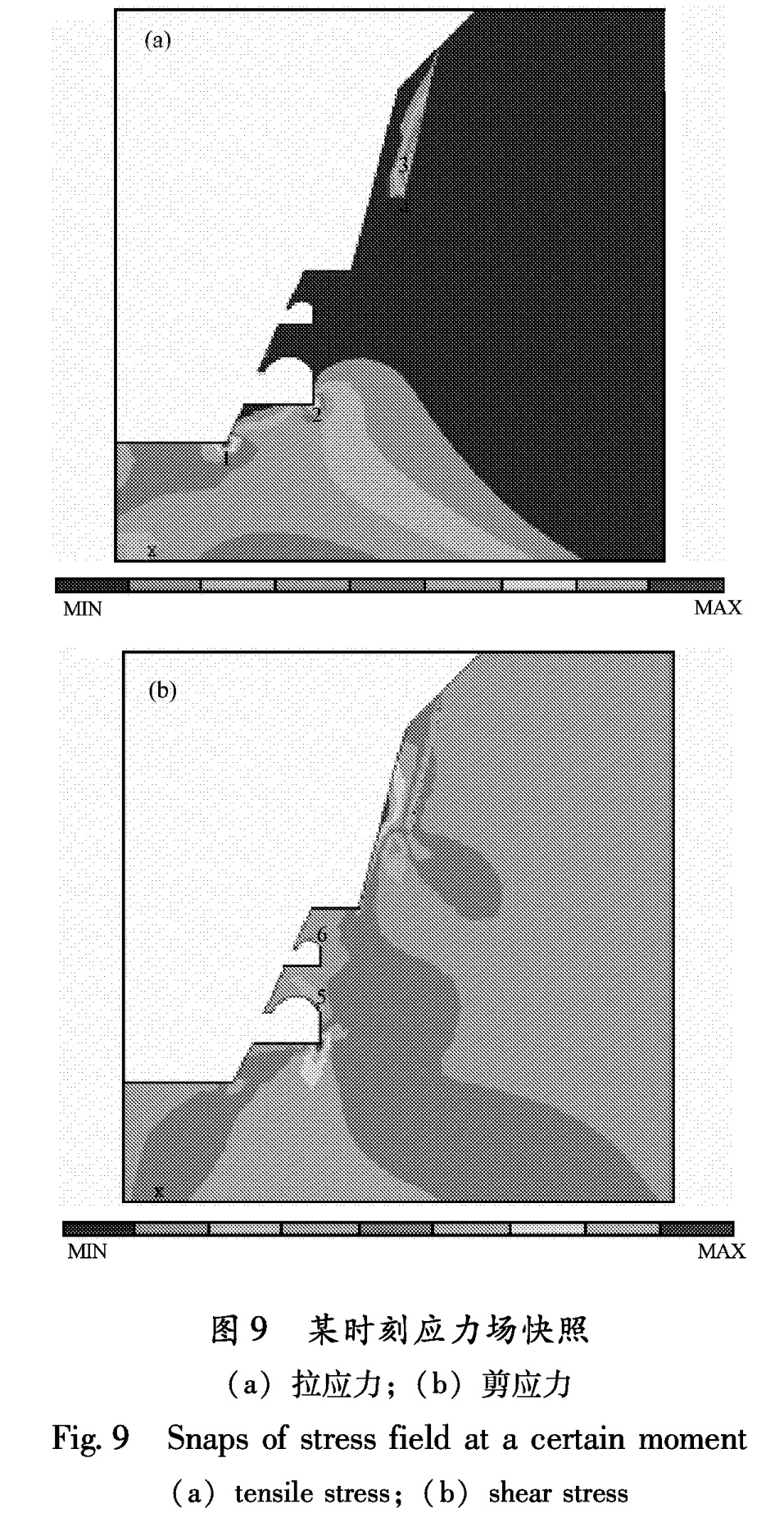
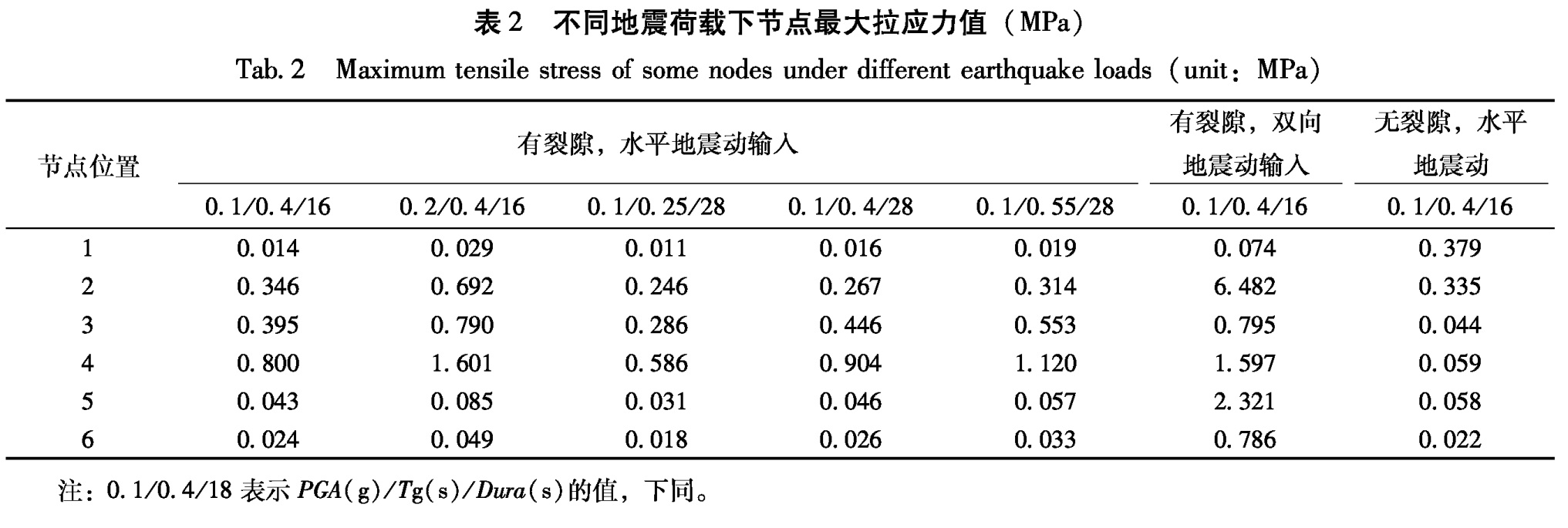
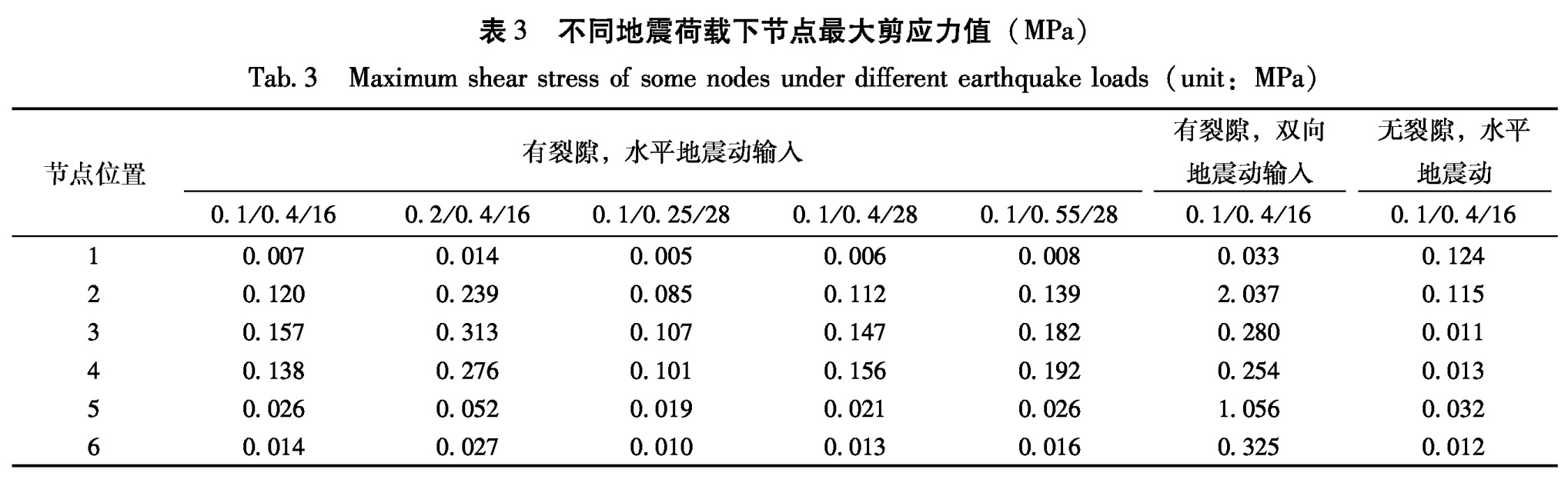
入),裂隙的存在与否对岩体的最大振动位移的影响非常显著。当考虑裂隙时,岩体的最大振动位移高达0.5 cm左右; 而无裂隙时,最大振动位移不足0.05 cm。3.2 围岩应力特征分析应力是反映岩体受力状态、判断岩体是否损伤破裂的最直接证据。从图9可以看出,在岩体转折处、洞窟脚点和窟顶、以及裂隙附近出现了应力集中,是岩体最有可能发生破坏的地方。同时,考虑到岩体的抗压强度很大(为123 MPa),基本上不可能发生压性破坏。故而,以下仅对应力集中区某些节点的拉、剪应力值分别进行了统计,结果列于表2和表3。
(1)地震动的不同工程特性对应力分布的控制
计算结果显示:对于任意节点,当地震动特征周期和持时相同时,峰值加速度(PGA)增大,拉应力和剪应力值均有所增加; 当PGA和持时相同时,特征周期加长,拉应力和剪应力值也均有所增加; 当PGA和特征周期相同时,持时大小对应力值基本没有影响。
(2)洞窟结构对应力大小的影响
2号和5号节点分别位于下层洞窟的脚点和窟顶附近,通过对比各种地震输入下两节点处的计算结果可以发现,洞窟脚点(2号节点)处的拉应力值和剪应力值均明显大于洞窟窟顶(5号节点)处的拉应力和剪应力值。说明转折大的部位的应力值会大于转折小的部位(穹窿形)的应力值。
6号节点位于上层较小洞窟的窟顶附近,通过比较发现,该节点的应力值总小于下层较大洞窟窟顶处的5号节点的应力值。表明洞窟尺寸对岩体应力有影响,尺寸越大,相似位置处的应力值越大。图9 某时刻应力场快照(a)拉应力;(b)剪应力
Fig.9 Snaps of stress field at a certain moment(a)tensile stress;(b)shear stress(3)考虑竖向地震动对应力大小的影响
相比单纯水平向地震动输入,当同时考虑水平向和竖直向地震动输入时,表中所有节点的拉应力和剪应力值均有不同程度的增加。影响最大的是2号节点,其拉应力值由0.35 MPa骤增到6.48 MPa,剪应力由0.12 MPa增加到2.04 MPa; 其次是5号节点,其拉应力值由0.043 MPa骤增到2.32 MPa,剪应力由0.026 MPa增加到1.06 MPa。需要说明的是,这种不同程度的增加,也可能反映了洞窟及其结构对控制整个应力场变化的重要意义。
表2 不同地震荷载下节点最大拉应力值(MPa)
Tab.2 Maximum tensile stress of some nodes under different earthquake loads(unit:MPa)注:0.1/0.4/18表示PGA(g)/Tg(s)/Dura(s)的值,下同。
表3 不同地震荷载下节点最大剪应力值(MPa)
Tab.3 Maximum shear stress of some nodes under different earthquake loads(unit:MPa)(4)有无裂隙存在对应力大小的影响
表中3号和4号节点在有无裂隙两种情况下的计算结果充分反映了裂隙对其周围岩体应力状态的控制作用。同样的水平地震动加速度输入下,有裂隙时两节点的应力值均大于无裂隙时两节点的应力值,其它节点受裂隙的影响较小。
最后,可以根据以下三个原则来判定岩体是否发生破坏:(1)如果岩体上的拉应力超过其抗拉强度,则发生单向拉裂破坏。当岩体中有裂隙存在,由于结构面的不抗拉特性,最易沿这组裂隙拉裂。(2)如果岩体上的压应力超过其抗压强度,则发生单向压裂破坏。(3)依据莫尔—库伦强度理论,对于脆性岩石,任一点发生剪切破坏时,破坏面上的剪应力必须大于临界剪应力。这里,临界剪应力(τf)等于材料内聚力(C)与作用于该剪切面上法向应力(σθ)引起的内摩擦阻力之和,即:
τf=C+σθ·tanφ.(5)
从表2和表3发现:(1)除了在同时考虑竖向地震动输入的情况下,下层洞窟脚点的拉应力值大于岩体的抗拉强度(5.85 MPa),会发生拉张破坏之外,其它情况下岩体的拉应力值均小于该值,因而是稳定的;(2)由于岩体的抗压强度非常大(123 MPa),所以不可能发生压性破坏;(3)由于岩体的剪应力最大为2.037 MPa,小于内聚力5.85 MPa,因此可以认为,在所有考虑到的情况之下,岩体都不会发现剪切破坏。
4 结论
(1)通过输入不同工程特性的地震动进行计算,研究发现:地震动峰值加速度越大,洞窟的振动位移和应力值明显增大; 反应谱特征周期越长,岩体振动位移和应力值也明显加大; 持时的大小对位移和应力值基本没有影响。
(2)同时考虑竖向地震动输入时,岩体的振动位移和应力值均有明显加强。对于有大量洞窟存在的岩体边坡,竖向地震动对其稳定性的影响可能会大于水平向地震动。
(3)洞窟结构对岩体应力有明显的控制作用。洞窟转折大的部位的应力值会大于转折小的部位的应力值; 洞窟尺寸对岩体应力有影响,尺寸越大,相似位置处的应力值越大。
(4)裂隙对岩体振动位移和应力也有明显的控制作用。裂隙的存在不同程度地改变了周围岩体的位移和应力值的大小,但对距其较远位置的岩体影响不大。
(5)根据岩体强度准则,认为只有在同时考虑竖向地震动输入时,下层洞窟脚点位置会发生拉张破坏。此外,裂尖处的拉应力为1.597 MPa,如果考虑裂隙处材料力学性能的折减,此处有可能也会产生拉张破坏并加以扩展,但这种危险性可以通过裂隙灌浆和预应力锚固等工程加固手段予以消除。
- 付长华,石玉成.2004.地震荷载下莫高窟围岩动态损伤特性研究[J].西北地震学报,26(3):266-273.
- 国家地震局震害防御司.1995.中国历史强震目录(公元前23世纪—公元1911年)[M].北京:地震出版社.
- 国家地震局震害防御司.1999.中国近代地震目录(公元1912年—1990年)[M].北京:中国科学技术出版社.
- 何开明,周健,王兰民,等.2003.化学灌浆黄土地基的抗液化性状研究[J].地震研究,26(4):396-399.
- 胡聿贤,高孟潭,杜玮,等.2001.中国地震动参数区划图宣贯教材[M].北京:中国标准出版社.
- 李海波,蒋会军,赵坚,等.2003.动荷载作用下岩体工程安全的几个问题[J].岩石力学与工程学报,22(11):1887-1891.
- 李海波,吴绵拔.1995.龙门石窟文物区岩体波动测试与分析[J].岩土力学,16(3):43-48.
- 牟会宠,杨志法,伍法权.2000.石质文物保护的工程地质力学研究[M].北京:地震出版社.
- 秋仁东,石玉成,李罡,等.2009.地震引发滚石灾害及其基本特征研究[J].地震研究,32(2):198-203.
- 秋仁东.2006.地震荷载作用下预应力锚索加固石窟围岩的动力响应研究[D].兰州:中国地震局兰州地震研究所.
- 石玉成,蔡红卫,徐晖平,等.2002.石窟围岩及其附属构筑物地震稳定性评价方法研究[J].西北地震学报,22(1):83-89.
- 石玉成,付长华,王兰民.2006.石窟围岩地震变形破坏机制的数值模拟分析[J].岩土力学,27(4):543-548.
- 王现国,彭涛,郭友琴,等.2006.龙门石窟变形破坏原因及保护对策[J].中国地质灾害与防治学报,17(1):130-132.
- 中国地震台网中心.中国地震台网(CSN)地震目录(2010-03-15)[2010-05-01].http://www.csndmc.ac.cn/newweb/data.htm#.
- GB/T 50011-2001.建筑抗震设计规范[S].