基金项目:地震行业专项:汶川8.0级地震建筑震害研究及震害数据库建设项目(201008006)和中国地震局地震科技星火计划项目(XH1021Y)共同资助.
(1.四川省地震局,成都 610041; 2.成都理工大学,地球探测与信息技术教育部 重点实验室,成都 610059; 3.中国国土资源部 航空物探遥感中心,北京 100083)
(1.Earthquake Administration of Sichuan Province,Chengdu 610041,Sichuan,China)(2.Key Laboratory of Geophysics & Information Technology of the Ministry of Education of China,Chengdu University of Technology,Chengdu 610059,Sichuan,China)(3.China Aero Ge
aeromagnetic anomaly; wavelet transform; multi-scale analysis; Mex file; mixed programming
备注
基金项目:地震行业专项:汶川8.0级地震建筑震害研究及震害数据库建设项目(201008006)和中国地震局地震科技星火计划项目(XH1021Y)共同资助.
阐述了小波多尺度分析原理和Mallat算法。针对以往MATLAB文件执行速度较慢的问题,提出了一种新的通过MEX文件来实现在MATLAB环境中调用C++源码程序的混合编程技术,并对球体磁异常叠加理论模型进行正演计算和对比研究,最后利用该方法对某测区的航磁异常进行分解,并展示两个阶次典型的航磁异常细节特征图。结果 表明:用小波分解得到的航磁异常细节特征图,同样起到了功率谱分解的作用,不但可以从异常细节图上清晰地圈闭出深大断裂带的赋存位置,而且在速度上较以往的单一计算方法也有了明显的提高,对今后类似地区数据处理具有较重要的参考价值。
We explain a multi-scale analysis of wavelet theory and Mallat Algorithm.In view of the previous slow pace of implementation for MATLAB files,We propose a new mixed programming technique to call C++ source process using MEX file in MATLAB environment.We make a calculation and comparison of magnetic anomalies superposition of the sphere theoretical model,and using the method to decompose the aeromagnetic anomalies of a certain measured area and its surrounding areas,we get two orders of the typical characteristics of aeromagnetic anomaly map.The results show that detail of aeromagnetic anomaly map obtained through wavelet decomposition also plays a role in the power spectrum analysis.The deep faults can be located on the anomalous map,hence,this map provide a reference for the similar regional data processing in future.
引言
在地球物理反演中,航磁异常是来自不同深度和不同尺度地质体位场的叠加反映,也是利用磁测资料进行构造分区的基础,如果不能对其做合适的分离,则难以解译场源体的物性参数和赋存范围等信息①(李才明,万新南,1996)。傅立叶分析法作为处理地球物理信号的主要工具只能获得函数的整体频谱,不能获得信号的局部特性,而小波分析提供了一种自适应的时—频同时局部化的分析方法,无论分析低频信号还是高频信号,它都能自动调节时—频窗,以满足实际分析的需要(李世雄,刘家琦,1994); 侯遵泽和杨文采(1997)使用小波多尺度分析方法对中国布格重力异常进行了分解,为研究地壳结构提供了证据; 高德章等(2000)使用小波多尺度分析方法对东海及邻区重力异常进行多尺度分解,解释了该区域沉积基底面、莫霍面形态等信息; 王文睿等(2009)使用小波多尺度分析对月球重力异常进行了分解,解释了月球内部的基本分层结构; 张先等(2006)利用小波变换技术对北京地区航磁异常进行多尺度分解,并在此基础上对北京市区的主要断裂进行了探讨。本文应用多尺度分析的特性,将信号分解成各种不同的频率成分或尺度成分,并通过伸缩、平移、聚焦到信号的任意单一细节,用MATLAB即可实现基于小波变换的各种分析计算,从而为航磁异常的处理开辟了一条新的途径(Mallat,Hwang,1992)。
MATLAB作为一种解释性的脚本语言,其编写的算法程序运行效率低下,尤其是涉及到循环迭代语句时,运行速度更加缓慢; 然而C++语言则表现出运行速度快、执行效率高的优势。笔者在小波分析原理的基础上,介绍了通过MEX文件实现MATLAB环境中调用C++算法程序来加快执行速度的可行性和细节要点,并在对球体理论模型磁异常正演计算的基础上采用混合编程技术,选择一个测区的实际航磁异常资料进行多尺度分析,不但得到了各种有利于地质解释的航磁异常特征,而且在速度上较以往也有了进一步的提高。我们根据航磁异常的处理结果,结合地质信息,对该地区的断裂的分布特征与性质和深部地质构造进行了初步的分析研究,取得了良好的效果,为正确认识区域的地球物理场特征提供了坚实的依据。
1 小波分析的方法原理
1.1 函数的小波变换设函数f(x)=∑m,n∈zWf(m,n)ψm,n(x),(1)
定义其小波变换为
Wf(a,b)={f,ψa,b}=1/((|a|)1/2)∫+∞∫-∞f(x)ψ^-((x-b)/a)dx,(2)
其中ψ(x)∈L2(R)称为小波函数或简称为小波,
ψa,b(x)=1/((|a|)1/2)ψ((x-b)/a),(a∈R,b∈R,a≠0),(3)
ψ(x)满足条件∫+∞∫-∞ψxdx=0。
令Cψ=∫+∞∫-∞(|ψ^(ω)|2)/(|ω|)dw,其中ψ^(ω)是ψ(ω)的傅立叶变换,相应的小波逆变换
f(x)=1/(Cψ)∫+∞∫-∞(da)/(a2)∫+∞∫-∞Wf(a,b)ψ(a,b)(x)db.(4)
取a=am0, b=nam0b0(m,n∈z,a0>1,b0>1)则有小波变换的离散形式
Wf(m,n)=a-m/20∫+∞∫-∞f(x)ψ(a-m0x-nb0)^-dx.(5)
1.2 多尺度分析原理和Mallat算法对于二维平面上的函数f(x,y),设{Vj}j∈z为一维多尺度分析,其尺度函数φ(x)和小波函数ψ(x)满足双尺度方程,令V2j=VjVj,则{V2j}j∈z构成一个二维多尺度分析,尺度函数为
φ(x,y)=φ(x)·φ(y),(6)
小波函数为{ψhf(x,y)=ψ(x)·φ(y),
ψvf(x,y)=φ(x)·ψ(y),
ψdf(x,y)=ψ(x)·ψ(y).(7)
令函数f(x,y)∈{V2j}j∈z, Ajf(x)表示V2j空间的低频细节部分, Dhjf(x)、 Dvjf(x)、 Ddjf(x)分别表示W2j空间中水平、垂直和对角线方向上的高频细节部分,则有
Aj f(x,y)=Aj+1 f(x,y)+Dhj+1 f(x,y)+
Dvj+1 f(x,y)+Ddj+1 f(x,y).(8)
上式中,{Aj+1 f(x,y)=∑m1,m2∈zsj+1m1,m2φj,m1,m2,
DTj+1 f(x,y)=∑m1,m2∈zdT, j+1m1,m2φTj,m1,m2,
(T=h,v,d).(9)
其中:{sj+1m1,m2=∑k1,k2∈zhk1-2m1hk2-2m2sj,m1,m2,
dh,j+1m1,m2=∑k1,k2∈zhk1-2m1gk2-2m2sj,m1,m2,
dv,j+1m1,m2=∑k1,k2∈zgk1-2m1hk2-2m2sj,m1,m2,
dd,j+1m1,m2=∑k1,k2∈zgk1-2m1gk2-2m2sj,m1,m2.(10)
对于二维航磁异常的小波多尺度分析则表示为
ΔT(x,y)=A0 f(x,y)=A4 f(x,y)+∑4j=1(Dhjf(x,y)
+Dvjf(x,y)+Ddj+1f(x,y)).(11)
再根据sj+1m1,m2~dd,j+1m1,m2,可以计算出其他空间中尺度函数的系数{sj}和小波函数的系数{dh,j}、{dv,j}、{dd,j},这样表达式可以简记为
ΔT(x)=A4ΔT(x)+D1ΔT(x)+D2ΔT(x)
+D3ΔT(x)+D4ΔT(x).(12)
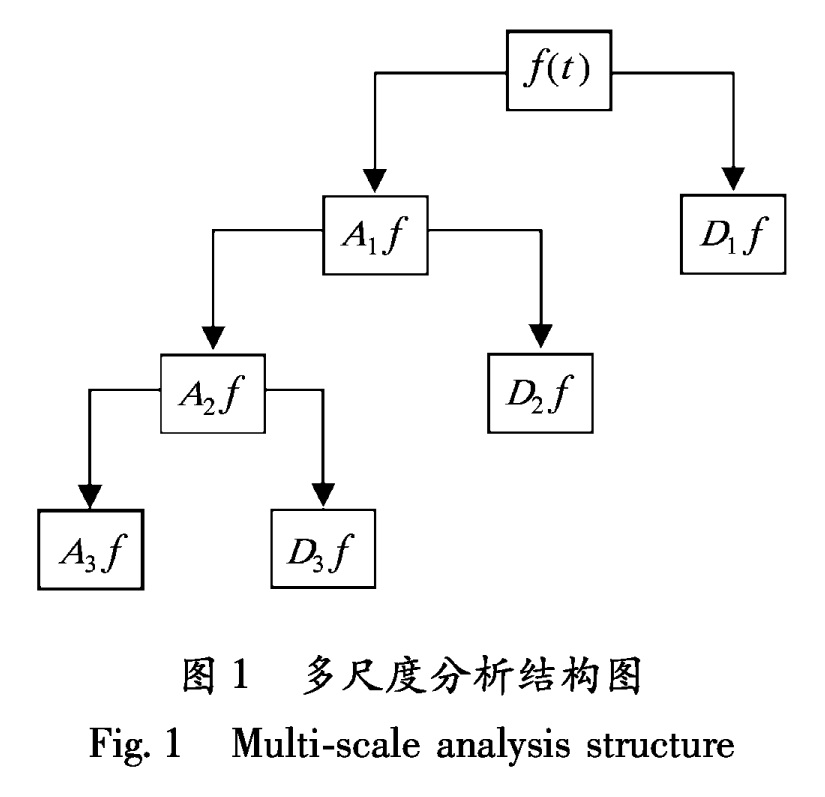
上述小波多尺度分析原理为我们提供了理论基础(张凤君,2007; 吴立辛等,2007; 裴韬等,2004),Malllat的快速算法给我们解决问题提供了一个途径。Mallat算法是将正交小波基的构造法统一起来,迭代出正交小波的构造方法和正交小波变换快速算法,其基本思想是:信号f(t)的某层小波分解是将f(t)以某个尺度j变换到空间L2(R)的两个正交子空间Vj和Wj上,由Vj得到离散逼近值Ajf,由Wj得到离散逼近值Djf,下一层分解中是以尺度j+1再将Aif分解到子空间Vj+1和Wj+1中,这样不断分解下去,即
f(t)=A1f+D1f=A2f+D2f+D1f=Anf+Dnf+Dn-1f+Dn-2f+…+D2f+D1f,(13)
从而对信号进行了多尺度分析,过程如图1所示。
1.3 MATLAB与C++混编计算(1)混合编程的环境
由于使用MATLAB 与C++混合编程涉及到两个软件,因此需要提供相应的外部程序接口并配置集成开发环境(张德丰,2009; 刘维,2007),MATLAB外部程序接口可以方便地完成与外部环境的交互,VC++可以通过dll方式提供应用程序接口。首先在MATLAB命令窗口输入Mex-setup根据提示进行安装,进行高级语言编译器的关联; 然后在VC++中增加MATLAB外部程序接口函数的安装路径,配置好集成环境后,就可以在一个软件的集成环境中进行程序编译调试。
(2)混合编程的编译细节
在混编计算操作中需要注意的是编译时的一些要点:首先在MATLAB命令窗口输入Mex-setup,根据提示进行安装,生成的mex文件,直接用mex*.cpp就可以输出*.dll文件,如果需要生成调试的mex文件,需用mex-g*.cpp,或生成*.dll文件; 接着运行->MSdev “路径下的*.dll文件”,打开VC++6.0窗口,在Project->Settings设置框,将“Executable for…”设为“C:\MATLAB701\bin\win32\MATLAB.exe”,就可以进行调试了,程序已在MATLAB7.01和VC++6.0环境下调试通过,运行结果如表1所示。
从表1中对比研究发现,MATLAB文件计算速度远比C++程序要慢,但是通过调用Mex文件执行后计算速度就加快了很多,此优越性为接下来用MATLAB实现基于小波变换提供了新的方法思路。
2 球体理论模型的正演计算与小波变换
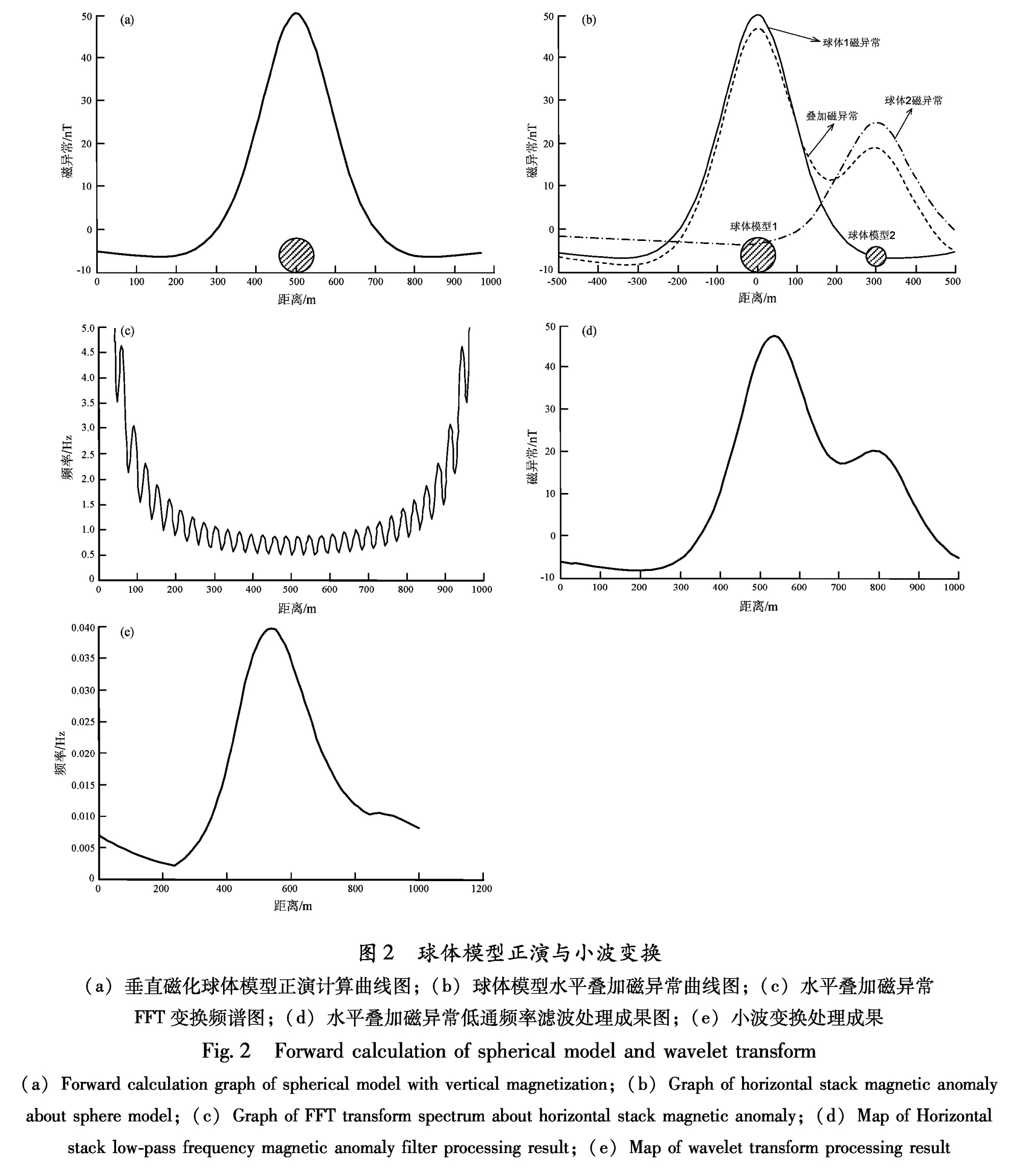
下面调用Mex文件在MATLAB环境中实现基于小波变换的各种处理。为了说明小波在提取深部场源体磁异常信号中的效果,我们在处理过程中设计了如下的球体理论模型,并与频率滤波做了对比研究,得到如下结果:设计球体理论模型中心埋深300 m,单位长度的有效磁矩为104 Am2,磁化倾角I取90°,即垂直向下磁化,正演计算得到球体模型的ΔT曲线(图2a)。
图2b中显示了球体1和球体2各自的磁异常曲线以及两个球磁性异常叠加后的曲线,其中,球体2位于球体1右侧300 m处,深度为250 m,有效磁矩为5 000×10-3 Am2; 图2c为对水平叠加磁异常进行快速傅立叶变换,然后再进行傅立叶反变换后的处理结果; 图2d为经过低通频率滤波处理得到的结果,可以看出该图没能很好地分离出两个球体的磁性异常,即对于该数学模型磁异常的提取,利用傅立叶频率滤波方法还不理想; 图2e为经过小波变换得到的水平叠加磁异常的处理结果,该图不仅能够明显反映出深部球体的磁异常曲线形态和埋藏位置,而且通过调用MEX文件实现MATLAB在处理计算的过程中简化了以往的多行代码,提高了运行速度。
图2 球体模型正演与小波变换
(a)垂直磁化球体模型正演计算曲线图;(b)球体模型水平叠加磁异常曲线图;(c)水平叠加磁异常
FFT变换频谱图;(d)水平叠加磁异常低通频率滤波处理成果图;(e)小波变换处理成果
Fig.2 Forward calculation of spherical model and wavelet transform(a)Forward calculation graph of spherical model with vertical magnetization;(b)Graph of horizontal stack magnetic anomaly about sphere model;(c)Graph of FFT transform spectrum about horizontal stack magnetic anomaly;(d)Map of Horizontal stack low-pass frequency magnetic anomaly filter processing result;(e)Map of wavelet transform processing result3 航磁异常的分解结果
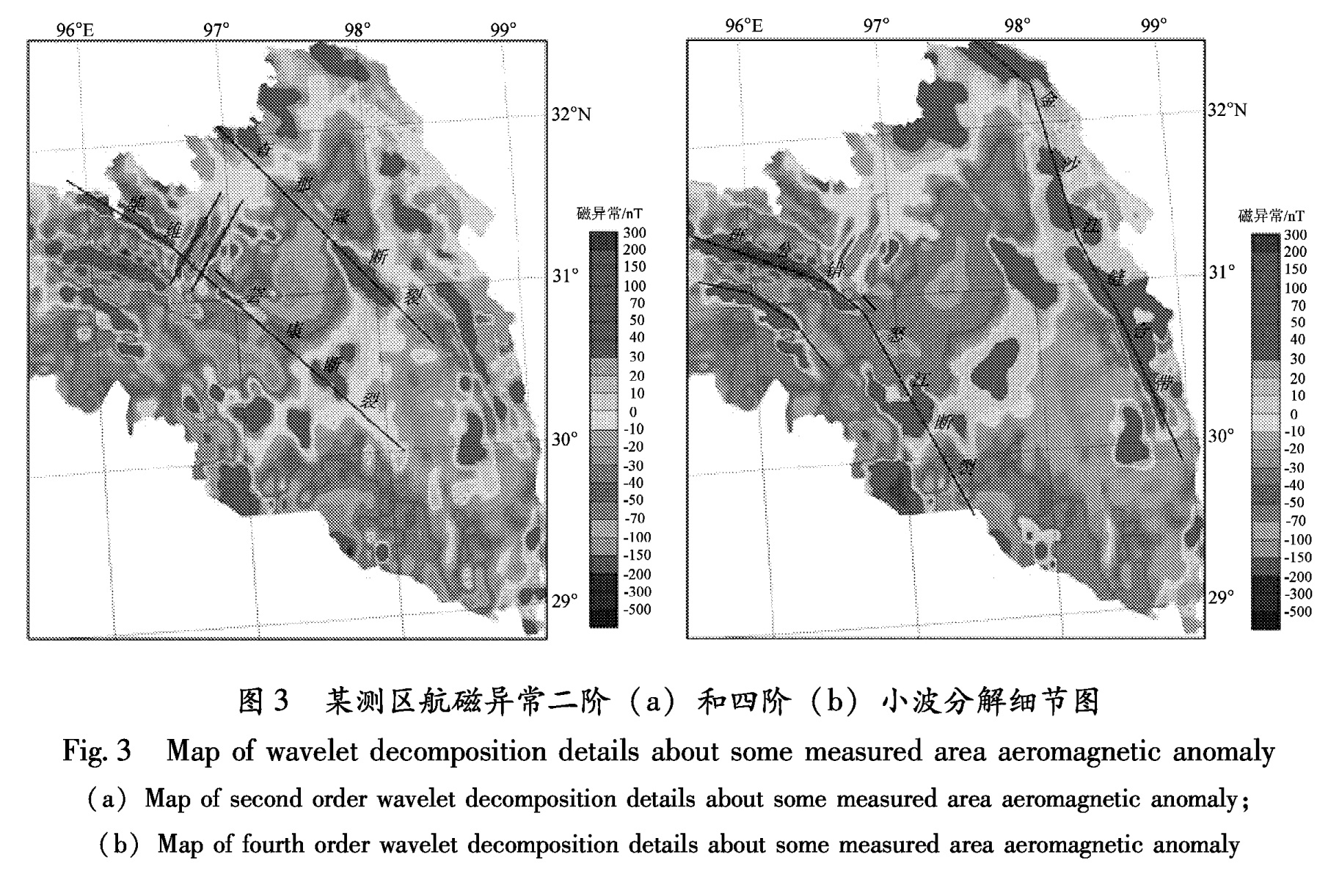
笔者依据上述方法原理分别对某测区航磁异常进行了处理。使用中国国土资源航空物探遥感中心1:100万的航磁数据,首先将数据合并进行预处理,包括正常地磁场校正、日变校正、高度校正,再通过小波多尺度分析对航磁异常进行处理和多尺度分析计算。计算过程如下:首先对航磁异常进行小波正变换,乘以选好的小波函数进行小波反变换,得到不同阶次的异常分解细节图,根据细节图就可推断区域内断裂体系的分布范围,在此展示两个典型细节的图像(图3a,b)。
需要说明的是,本次处理过程中所使用的计算方法对于一个区域内叠加异常的分解与其他位场分离方法一样,单一尺度的细节不可能完全分离出某一埋深和规模的地质体的异常,这不仅由于不同埋深和规模的场源体频谱重叠,还因为此次处理的区域数据量大、地质体的介质特性复杂。本文只是展示所取得的一些典型的试验性成果。
从图3a可以看出异常圈闭尺度较小,分布离散杂乱且无规律,局部串珠状的磁异常主要因为观测数据中包含高频噪声干扰以及浅层岩石磁性特征和岩浆活动较为频繁。深大断裂的位置和走向不明显,因此对一些无明显特征的磁异常带不能做出正确的解释推断,只能对较明显的条带状和块状磁异常区进行推断,认为它们是柴维—芒康断裂及查那隆断裂。经过四阶小波分解得到图3b,从中可以清晰地看出浅部规模小的断裂信息消失了,保留下来的是规模较大、切割较深的大断裂。最明显的正负磁异常相间的条带状异常为班公错—怒江断裂及金沙江断裂。总体走向近北西西向、呈波状延伸的班公错—怒江断裂带分布较连续,主要特征为负背景场上叠加有众多正负伴生异常,磁异常多以紧密线性排列,规模较大,峰值一般为100~300 nT,它是一条切割很深的断裂,向西磁异常逐渐减弱,直至与背景磁场连成一片,反映了断裂带南西、北东两侧具有相同基底的特点; 而位于测区北缘的金沙江缝合带的特征幅尤为明显,在研究区内向南偏转,呈断续的带状分布,峰值明显高于背景场,它同样是一条切割很深的大断裂,推断其为幔源断裂。
从图3可以看出,从南到北航磁异常表现出明显的分区性和分带性,这些特征是该区特有的地质构造及赋存状态的综合反映,由此可见,经过小波多尺度分解计算得到的断裂信息更加丰富、更加清晰。
图3 某测区航磁异常二阶(a)和四阶(b)小波分解细节图
Fig.3 Map of wavelet decomposition details about some measured area aeromagnetic anomaly(a)Map of second order wavelet decomposition details about some measured area aeromagnetic anomaly; (b)Map of fourth order wavelet decomposition details about some measured area aeromagnetic anomaly4 结论
(1)相对于传统的数据处理和反演方法,小波分析方法具有传统方法所不具备的优势,尤其适用于重磁异常的尺度分解及地质解释,无论是浅部断裂还是深部壳源、幔源断裂等大型断裂,只要在断裂两侧存在磁性差异,就会在不同阶次的航磁异常细节图上有所体现,加之在抗磁异常处理过程中使用了C++与MATLAB混合编程的新技术,解决了MATLAB不便于处理大量带有循环结构的问题,提高了运行的速度。
(2)不同尺度的异常细节图像反映出不同深度的断裂构造信息,但细节图还未能反映场源体的埋深信息,笔者基于位场波数域的理论,并结合功率谱计算等频谱分析方法或是地震测深反演手段计算出小波细节所对应的的场源深度,从而达到了解断裂在不同深度的赋存状态和三维空间的分布状况。
(3)笔者通过混合编程实现了小波分析的计算和执行速度的提高,是地球物理数据处理环节上(尤其是位场勘探数据计算领域)的新尝试,并取得了初步成果,对于该领域存在的一些问题,还需要更深入细致的研究。
- 高德章,侯遵泽,唐建.2000.东海及邻区重力异常多尺度分解[J].地球物理学报,43(6):842-849.
- 侯遵泽,杨文采.1997.中国重力异常的小波变换与多尺度分析[J].地球物理学报,40(1):85-95.
- 李才明,万新南.1996.物探异常的间接模式识别[J].成都理工学院学报,23(1):91-99.
- 李世雄,刘家琦.1994.小波变换和反演数学基础[M].北京:地质出版社.
- 刘维.2007.精通MATLAB与C/C++混合程序设计[M].北京:航空航天大学出版社.
- 裴韬,周成虎,汪闽,等.2004.用二进小波分析方法对华北地区强震活动期的研究[J].地震研究,27(1):37-42.
- 王文睿,李雯,鄢建国,等.2009.月球重力异常的小波多尺度分析[J].地球物理学报,52(7):1693-1699.
- 吴立辛,卫定军,李国斌,等.2007.小波分析方法在宁夏短水准资料分析中的应用[J].地震研究,30(1):49-53.
- 张德丰.2009.MATLAB与外部程序接口编程[M].北京:机械工业出版社.
- 张凤君.2007.东北地震区地震趋势的小波分析[J].地震研究,30(2):134-141.
- 张先,赵丽,刘天佑等.2006.北京地区航磁异常的多尺度分解及断裂研究[J].地震学报,28(5):504-511.
- Mallat S,Hwang W L.1992.Singularity detection and processing with wavelets[J].IEEE,38(2):617-643.