基金项目:中国地震局2009年震情跟踪重点定向合同制工作任务(2009010104)资助.
(Earthquake Administration of Anhui Province, Hefei 230031,Anhui,China)
accelerating strain release; time-to-failure analysis; precursory event; critical radius; East China
备注
基金项目:中国地震局2009年震情跟踪重点定向合同制工作任务(2009010104)资助.
根据华东地区的地震活动特点,定义较简单的半径搜索方法,遵循一定的准则挑选出1976年以来华东地区满足震前累积应变加速释放模型(ASR)的14次ML≥4.5地震序列。将“破裂—时间分析”法的非线性方程分成两个线性方程,采用线性最小二乘法拟合参数k/m与主震矩的经验关系,确定华东地区的ASR模型,并用来预测主震的时间和震级。经检验该方法预测震级误差约为±0.3,发震时间误差约±1.68 a。
According to the characteristics of seismic activity in East China, we define a simple approach of searching radius and choose fourteen ML≥4.5 earthquake sequences since 1976 in East China which satisfy the pre-seismic Accelerating Strain Release(ASR)model. We express the nonlinear time-to-failure analysis equation with two linear equations and fit the empirical relation between the coefficient k/m and the main seismic moment tensor by means of Linear Least Square method in order to construct ASR model of East China for the prediction of the time and magnitude of the main shock in East China. Comparing the magnitude and the original time from the ASR model with the ones of the occurred strong shocks, we find that the magnitude error is ±0.3 and the time error is ±1.68 years.
引言
大地震前的矩释放加速现象(Accelerating Moment Release,简称AMR)在地震预测研究中展示了较好的应用潜力,引起地震学家的广泛关注(Skyes,Jaumé,1990; Bufe,Varnes,1993; Kno-poff et al,1996; Jaumé,Skyes,1999)。Varnes(1989)、Bufe和Varnes(1993)将重整化群的思想应用到AMR研究中,提出用累积地震矩与时间之间的“破裂—时间”逼近关系来定量描述这一现象,通过“破裂—时间分析”方法进行地震预测,并通过对旧金山湾区的强震研究表明,用累积Benioff应变(CBS)对加速模型进行拟合,以构造累积Benioff应变的加速释放模型(Accelerating Strain Release,简称ASR),比用地震矩释放能更准确地对目标地震的发生时间及震级进行预测(Bufe,Varnes,1993)。Bowman等(1998)利用使震前CBS释放曲线的幂率和线性拟合的均方根残差比最小来定量地确定计算AMR或ASR的“临界”时、空尺度,这使得利用AMR或ASR现象进行回溯性检验的“破裂—时间分析”方法具有了实际的可操作性。国内外已将“破裂—时间分析”方法应用于诸多震例(Bufe,Varnes,1993; Brehm,Braile,1998,1999; Mignan,Giovambattista,2008; 杨文政,马丽,1999; 秦嘉政,钱晓东,2004; 蒋海昆等,2009; 蒋长胜,吴忠良,2009; 钱晓东,2010),表明该方法不仅对于强震和发生在板块边缘的地震,而且对于中强以上地震和发生在板内地震活动带的地震均有较好的预测效果。
近年来,围绕AMR或ASR究竟是不是一种可靠和带有普遍性的地震前兆的争论也逐渐升温(Bowman et al,1998; Jiang,Wu,2006)。一方面,“最优化”搜索得到的AMR“临界”时、空尺度是不是真正的“孕震”时、空尺度; 另一方面,震前AMR现象作为一种可能的地震前兆是否具有普遍性。Jiang和Wu(2006)使用固定的时间尺度和多空间尺度,系统研究了中国大陆MS6.0以上地震事件前AMR现象的普遍性问题,发现60%的中强震前存在稳定的地震矩释放加速现象。蒋海昆等(2009)以中国大陆21次6.8级以上地震为例,得出中国大陆7级左右地震前地震应变释放模式具有复杂、多样性。
华东地区(29°~37°N,113°~124°E)是大地震较少的地区,有历史记载以来共发生5次MS7.0以上的强震,最大为1668年山东郯城MS8.5地震,1970年以来共发生MS6.0以上地震3次,MS5.0以上地震14次,MS4.0以上地震70次(资料截止到2010年)。迄今为止,对华东地区AMR或ASR现象的研究仅限于1668年山东郯城MS8.5级地震和1846年黄海MS7.0地震(李强,2000),并没有涉及到中强以上地震的情况,而对中强以上地震的研究对该区域更具现实意义。本文将在上述研究的基础上,深入研究华东地区中强以上主震的特点,定义较简单的搜索半径的方法,遵循一定准则,挑选出震前满足ASR现象的地震序列,利用挑选出的地震序列的主震矩和参数k/m之间的强相关性和线性拟合确定参数m的方法,将“破裂—时间分析”方程的参数由4个减小到2个,确定华东地区的ASR模型,通过模拟实际观测资料来预测主震的时间和震级,以期揭示出该区域地震前兆事件活动的一些规律。
1 “破裂—时间分析”方法的基本原理
“破裂—时间分析”方法是通过幂指数关系来定量描述AMR或ASR现象,利用给定区域的前兆性地震活动来预测未来地震时间和强度的一种中期地震预测方法,且用累积Benioff应变比地震矩的预测效果更好(Bufe,Varnes,1993)。本文采用Bufe和Varnes(1993)、Brehm和Braile(1999)的表示方法
∑E1/2=Kpe+Kms-[k/m](tf-t)m,(1)
将Benioff应变定义为地震波能量的平方根。式中∑E1/2是t时刻在选定区域内的累积Benioff应变(CBS); 地震序列的CBS由Kpe和Kms组成,Kpe代表前兆事件的CBS,Kms代表主震的Benioff应变。式(1)中有4个未知参数(Kms,tf,k,m),tf是预测主震的破裂时间; k和m是常量,且m≠0,幂指数m的大小表示了CBS释放曲线类型,当m<1时为加速,m越小,加速特征越明显,m>1时为减速,m=1时为线性。
在计算由(1)式地震波能量的平方根定义的Benioff应变时,采用由Gutenberg和Richter(1956)给出的地震波能量与震级的转换关系
lgE=1.5MS+4.8.(2)
由于地震目录中的震级为体波震级ML,可利用经验关系式转换为面波震级MS
MS=1.13ML-1.08.(3)
假定每个主震的前震个数为N,对第i(i=1~N)个前震将(1)式整理为
lg(Kpe+Kms-∑ij=1(Ej)1/2)i=lg(k/m)+mlg(tf-ti),(4)
或简单的线性形式
y=p+qx.(5)
式中p=lg(k/m), q=m, x=lg(tf-ti), y=lg(Kpe+Kms-∑ij=1(Ej)1/2)i。因由主震和前震可确定x和y,故可计算出N组(xi,yi)数据,这样由线性最小二乘法可以拟合出斜率m。
Brehm和Braile(1998,1999)指出系数k/m的对数和主震地震矩M0的对数之间存在一种线性关系
lg(k/m)=AlgM0+B.(6)
式中地震矩M0与震级MS的转换关系(杨文政,马丽,1999)为
lgM0=1.5MS+9.14.(7)
分别将(4)式中拟合的m值和(6)式的k/m值代入式(1)式,于是未知参数由4个(Kms,tf,k,m)减到2个(Kms,tf)。
2 资料及数据处理
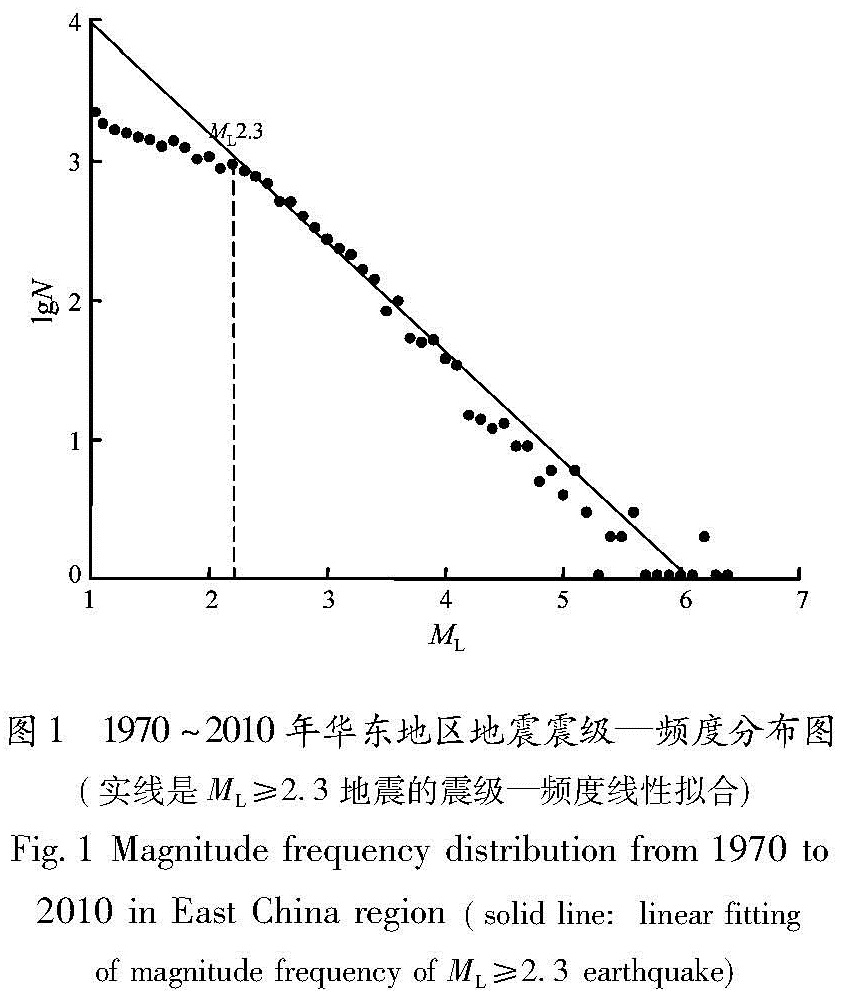
2.1 资料及ASR地震序列判别研究区域为华东地区(29°~37°N,113°~124°E),使用由中国地震台网中心提供的1970~2010年的ML≥1.0地震目录,震级统一为体波震级。从其震级—频度分布(图1)可以看出曲线在ML≤2.3时出现拐头现象,说明整个研究区域ML≥2.3地震记录相对完整,为了保证每个震例所在相对较小区域资料的完整性,本文使用ML≥2.5地震目录。
为了保证结果的可靠性,在挑选ASR现象的主震及其前震时遵循下面的准则:
(1)前震事件是从目标主震发震时刻前最佳持续时间段内,以目标主震的震中为中心,搜索半径的圆域内,震级在目标主震两个震级单位内的地震事件,由于本文使用ML≥2.5地震目录,因此主震震级可以从ML4.5开始。图1 1970~2010年华东地区地震震级—频度分布图(实线是ML≥2.3地震的震级—频度线性拟合)
Fig.1 Magnitude frequency distribution from 1970 to 2010 in East China region(solid line:linear fitting of magnitude frequency of ML≥2.3 earthquake)(2)至少有10次前震,其震级必须大于完整震级,考虑到震前至少应有6 a左右的资料以进行ASR模拟,因此选择的主震的发震时间从1976年开始。
(3)前震序列不含任何扰动事件,根据华东地区的地震活动特性,将扰动事件定义为小于等于主震0.5个震级单位内的地震,因此前震的震级范围是主震的两个震级单位到0.5个震级单位内。
(4)主震之间相互独立。在确定ASR的“临界”时、空尺度时,为了避免前震序列中含有扰动事件而使加速曲线被截断,本文定义搜索半径R为主震与小于等于主震0.5个震级单位内的前震的最近距离。
遵循上述准则挑选出主震和前震序列后,尚需对前震序列的加速或减速特征进行判定。一般以曲率参数C对观测资料的加、减速特征进行判定,曲率参数C定义为对累积Benioff应变进行幂率拟合的均方差与线性拟合的均方差之比(Bowman et al,1998),即
C=(幂率拟合的均方差)/(线性拟合的均方差).(8)
式中C<1表明幂率拟合结果优于线性拟合结果,即实际观测数据加速或减速的特征较为明显,C越小,模型的加、减速特征越明显。当C<1时且m<1为地震应变加速释放; 当C>1时,线性拟合结果优于幂率拟合结果,表明观测数据与幂率关系式(1)不相符。本文的前震序列均从1970年1月开始搜索,对所有满足10次以上前震的地震序列计算C值,当C<1且m<1时,最小C值对应的持续时间为加速序列的最佳持续时间,即地震应变加速释放序列为在最佳持续时间、搜索半径和震级范围内的10次以上前震事件和主震构成的序列。
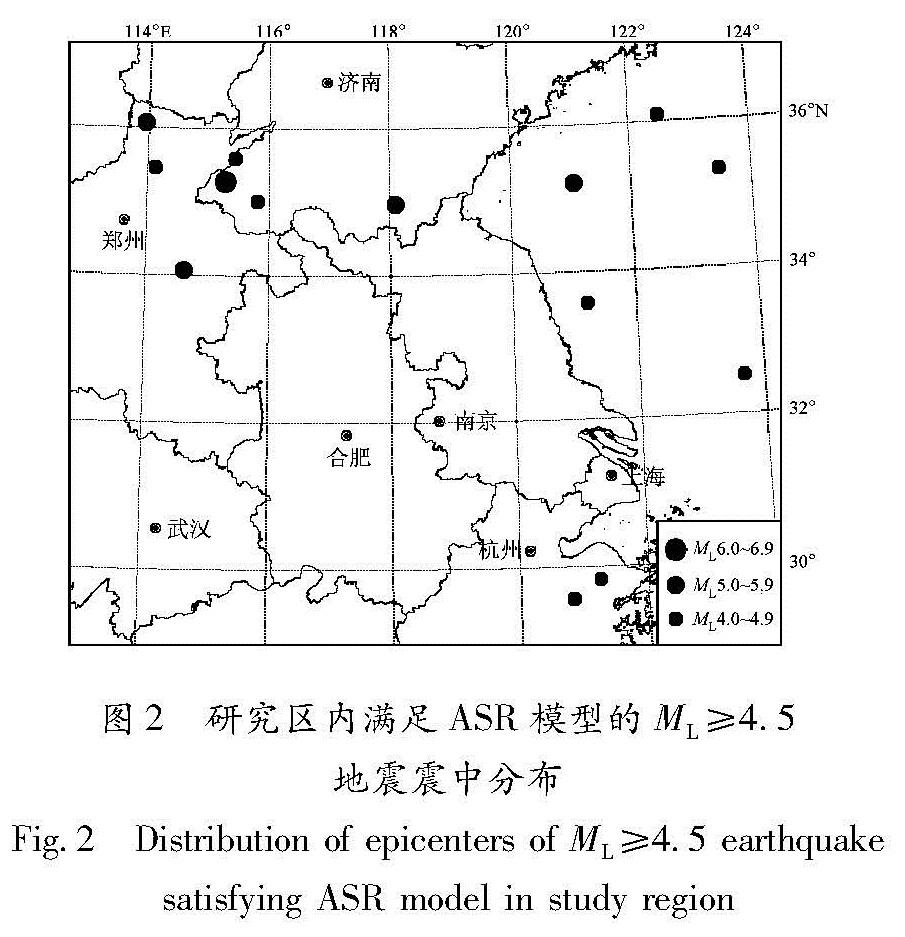
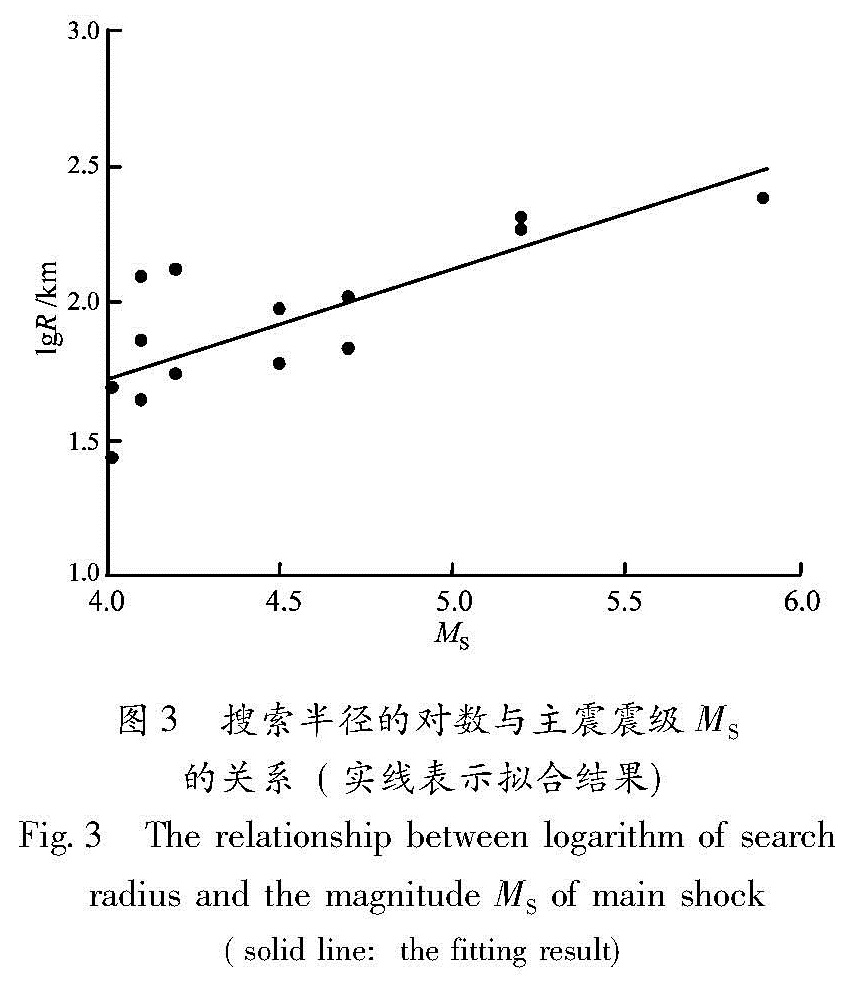
2.2 华东地区的ASR模型1976~2010年华东地区共发生47次ML≥4.5地震,其中29次分布在陆域。满足上述判定条件的主震有14次,其中陆域9次(图2)。对于每个地震应变加速释放序列,由式(4)可以拟合出m和k/m,由(8)式拟合出C值,表1列出了这14次主震的参数和拟合结果。搜索半径R在27~243 km范围内,图3显示搜索半径的对数与主震的大小(用MS表示)呈线性趋势,斜率为0.38,这与Wang等(2004)综合多项研究数据拟合的斜率相同,表明本文定义搜索半径的合理性。持续时间在5.5~31.0年之间,与主震震级关系不明显,m值在0.059~0.428之间,曲率C值在0.35~0.95之间。
图2 研究区内满足ASR模型的ML≥4.5地震震中分布
Fig.2 Distribution of epicenters of ML≥4.5 earthquake satisfying ASR model in study region图3 搜索半径的对数与主震震级MS的关系(实线表示拟合结果)
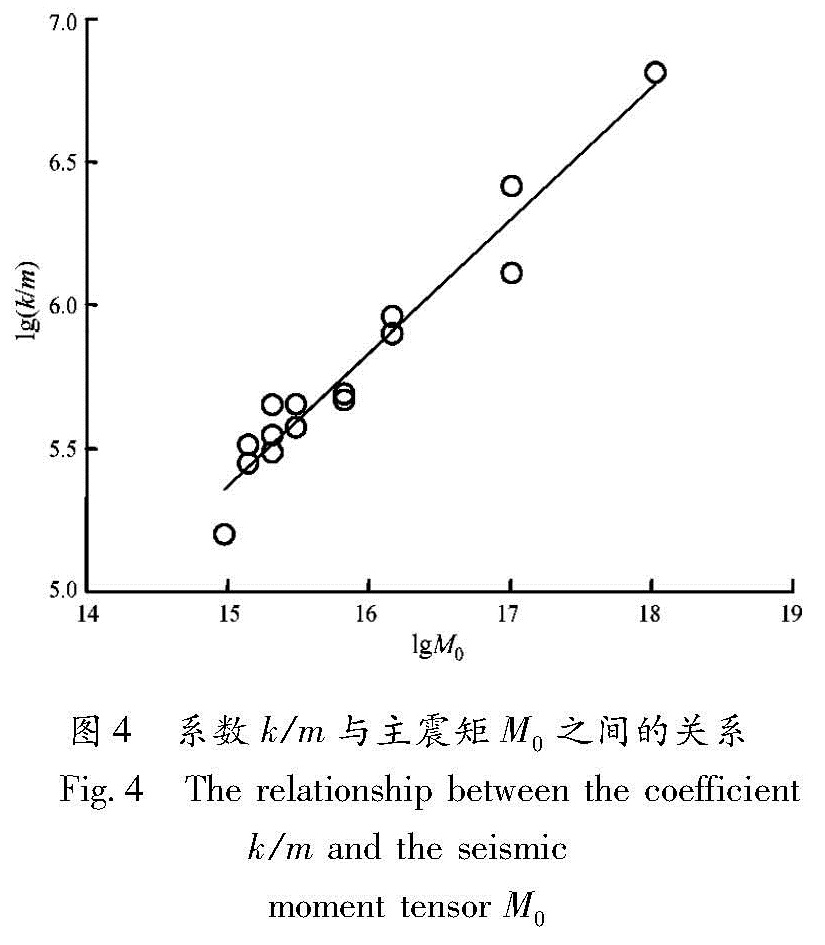
Fig.3 The relationship between logarithm of search radius and the magnitude MS of main shock(solid line:the fitting result)moment tensor M0图4 系数k/m与主震矩M0之间的关系
Fig.4 The relationship between the coefficient k/m and the seismic表1 华东地区满足ASR模型的14次地震序列的主震参数及拟合结果
Tab.1 Fitting result and main shock parameters of 14 earthquake sequences satisfying with ASR model in East China region图4中14次具有CBS加速释放的前震序列的k/m(表1)的对数与主震矩M0的对数显示较强的线性关系,采用线性最小二乘法拟合(6)式,拟合的相关系数为0.977,给出如下关系
lg(k/m)=0.464lgM0-1.59.(9)
由(4)式可以得到m值,将(9)式代入(1)式,系数k/m与主震矩有关,这样(1)式中的未知参数为Kms和 tf,由此确定出华东地区的ASR模型。
2.3 模拟结果在华东地区的ASR模型中,未知参数为Kms和tf,因此采用在Kms和tf的一定范围内进行双参数搜索求解。对于每个主震,取最后一个前震的发震时间加0.02 a作为起始时间(避免对零取对数),往后取4年作为预测时间范围,震级范围取主震上下1个震级单位。分别以时间和震级为横轴和纵轴,均以0.01为步长网格化,将每个格点对应的破裂时间(tf)和主震能量(Kms)代入(1)式可以计算出每个前震的∑(Ej)1/2calc.,与实际释放值进行比较,由下式计算出均方根(RMS)误差值
RMS=(1/N∑Nj=1 [(∑Ej)calc.-(∑Ej)obs.]2)1/2.(10)
先计算出每个格点的RMS值,然后通过除以整个网格的最小RMS值进行归一化,归一化后的RMS值最小值为1,画出归一化的RMS值等值线图。最小均方根误差值域区代表“最佳拟合”解的集合,取RMS最小值对应的震级和时间为预测值。这种通过分析均方根误差等值线图而不仅仅依据“单一的、最佳拟合”解的方法避免了多个可能解。
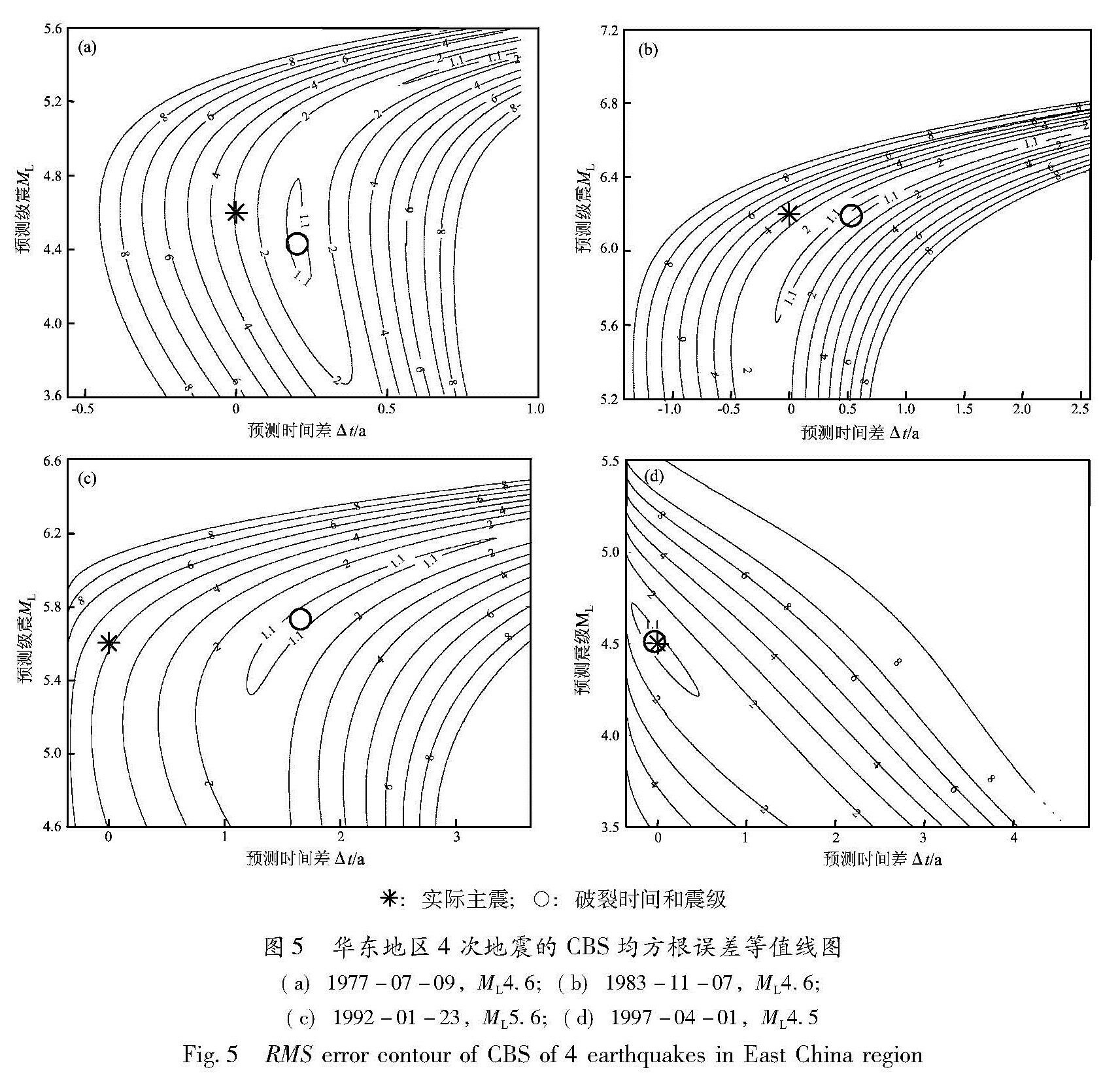
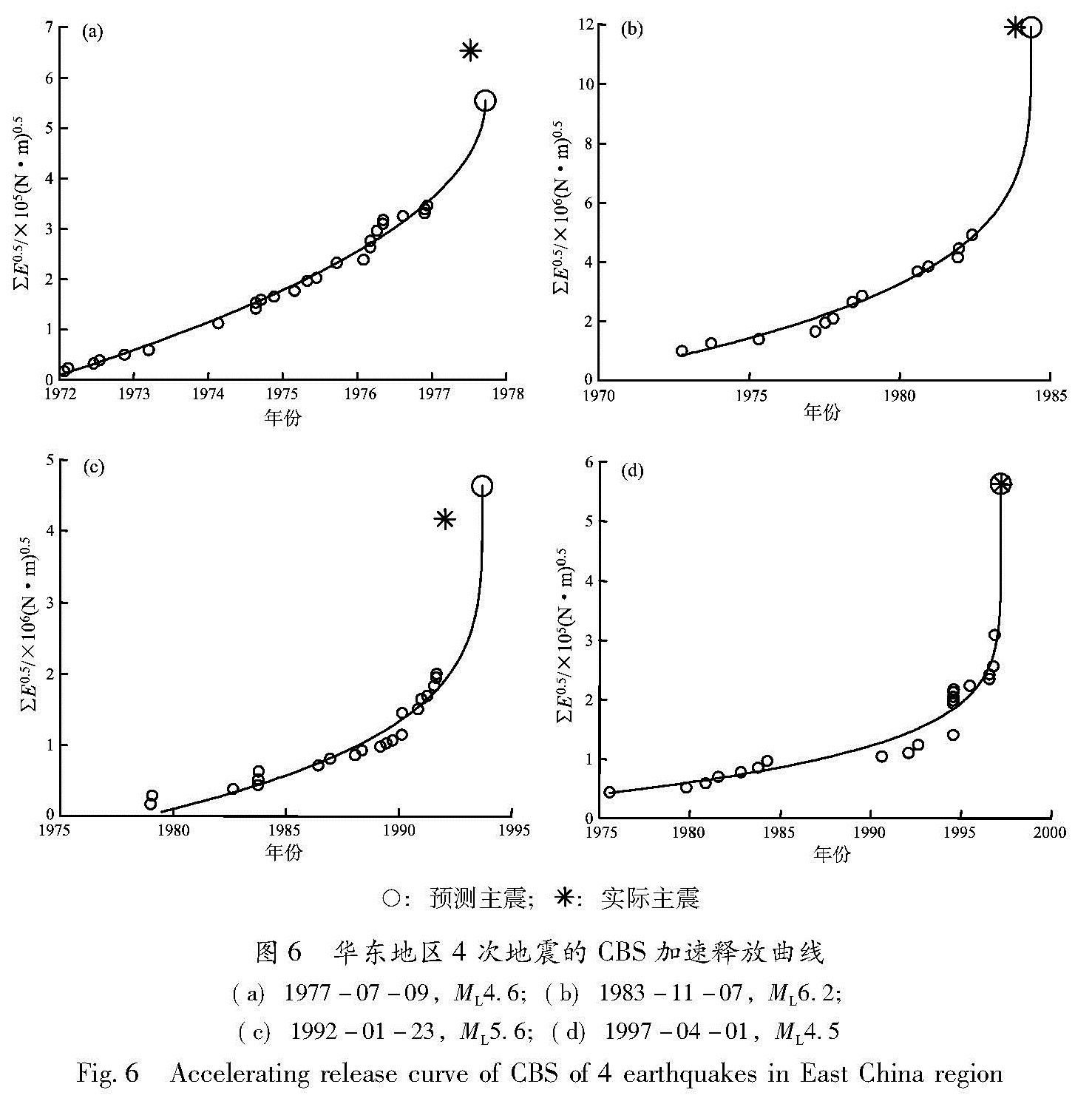
图5给出了4次地震的累积Benioff应变的均方根误差等值线图(为使图像清晰,RMS>10不做图),其中陆域和海域各2次。图中横坐标为预测破裂时间与实际主震发震时间之差Δt,单位为年,正数表示预测的主震破裂时间滞后,负数表示预测的主震破裂时间提前,纵坐标为预测震级。根据预测时间和震级由(1)式模拟的CBS曲线见图6中实线,空心圆点表示实际释放的CBS。表2给出了用华东地区的ASR模型模拟的14次主震事件的预测时间和预测震级。
:实际主震; ○:破裂时间和震级
图5 华东地区4次地震的CBS均方根误差等值线图(a)1977-07-09,ML4.6;(b)1983-11-07,ML4.6; (c)1992-01-23,ML5.6;(d)1997-04-01,ML4.5
Fig.5 RMS error contour of CBS of 4 earthquakes in East China region○:预测主震;:实际主震
图6 华东地区4次地震的CBS加速释放曲线(a)1977-07-09,ML4.6;(b)1983-11-07,ML6.2; (c)1992-01-23,ML5.6;(d)1997-04-01,ML4.5
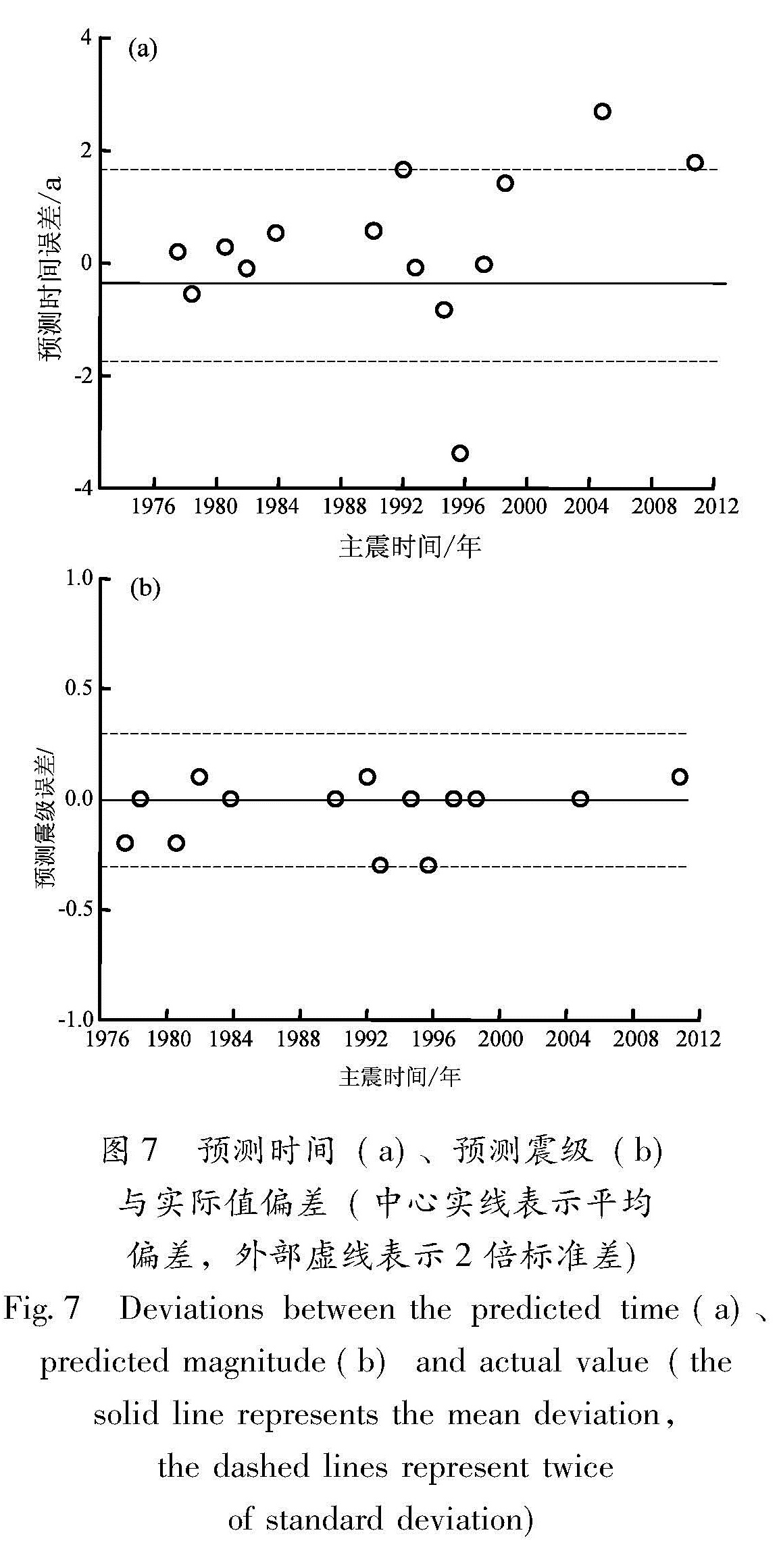
Fig.6 Accelerating release curve of CBS of 4 earthquakes in East China region2.4 误差分析对预测时间、预测震级与实际值的偏差进行了统计分析,偏差值为预测值减实际值(图7)。除了1995年9月20日山东苍山ML5.6地震的预测时间偏差为-3.38 a外,其余绝对时间偏差小于2.69 a。2倍标准差给出的统计时间误差为±1.68 a,分析表明1995年苍山ML5.6地震前5 a内无满足条件的前震事件,最后一次前震为1990年8月1日山东苍山ML4.4,预测时间比实际发震时间提前较多; 震级绝对偏差小于0.3级,2倍标准差给出的统计震级误差为±0.3级。因此这种方法对3 a尺度的中期地震预测效果较好,表明该模型适合于模拟华东地区的地震活动。
3 结论与讨论
对AMR或ASR的“临界”时、空尺度一般采用“最优化”的搜索结果,但是这种“最优化”搜索仅仅是对数据本身的拟合而言,一个明显的问题是相同构造区域和相近震级大小的强震的“临界”时、空尺度差异过大(蒋长胜,吴忠良,2009)。本文采用主震与小于等于主震0.5个震级单位内的前震的最近距离作为搜索半径,搜索半径的对数与主震的震级呈线性关系,斜率为0.38,Wang等(2004)综合多项研究数据拟合的斜率相同,表明这种搜索半径的合理性。采用曲率参数C和幂率指数m综合判别前震序列CBS释放的加、减速特征,最小C值对应的加速序列的搜索时间为最佳搜索时间。按照上述准则挑选出华东地区震前满足ASR模型的14次ML≥4.5地震序列,利用这14次地震序列拟合出k/m与主震矩的经验关系,确定华东地区的ASR模型。
利用华东地区的ASR模型对14次地震进行回顾性预测,预测震级误差约为±0.3级,预测时间误差约为±1.68 a,表明该方法可以作为一种有效的中期预测方法。
在挑选主震时,根据华东地区的地震活动特点遵循了一定的判别准则,保证了模拟结果的可靠性。华东地区1976年以来的47次ML≥4.5独立性地震事件中有14次满足ASR模型,仅占30%,这是因为地震应变释放模式具有复杂、多样性。蒋海昆等(2009)以中国大陆21次6.8级以上地震为例,研究得出中国大陆7级左右地震前中小地震应变释放模式可分为5类,其中“外围增强,内部减弱”的减速的应变释放占38%,“外围减弱,内部增强”的加速的应变释放占19%,仅能检测出加速特征的应变释放占14%,仅能检测出减速特征的应变释放占24%,仅有一例呈现出应变匀速释放特征。本文仅对14次满足ASR模型的地震进行了模拟,对华东地区其它应变释放模式有待进一步研究。
本文的研究尚不能对未来主震位置做出预测。为了将这种预测技术运用到实际的地震预测预报工作中,还需要进一步将开展主震位置搜索技术的研究。
- 蒋长胜,吴忠良.2009.强震前的“加速矩释放”(AMR)现象:对一个有争议的地震前兆的回溯性震例研究[J].地球物理学报,52(3):691-702.
- 蒋海昆,苗青壮,董祥,等.2009.中国大陆7级强震前中小地震应变释放特征[J].地震,29(3):1-10.
- 李强.2000.华东地区地震活动的加速模型分析[J].西北地震学报,22(4):419-423.
- 钱晓东.2010.破裂时间法在云南小江断裂带强震预测中的应用[J].地震研究,33(2):138-146.
- 秦嘉政,钱晓东.2004.利用前兆事件对云南地区地震进行中短期预测研究[J].地震学报,26(2):140-150.
- 杨文政,马丽.1999.地震活动加速模型及其在中国的应用[J].地震学报,21(1):32-41.
- Bowman D D,Quillon G,Sammis C G,et al.1998.An observational test of the critical earthquake concept[J].JGR,103(NB10):24359-24372.
- Brehm D J,Braile L W.1998.Intermediate-term earthquake prediction using precursory events in the New Madrid Seismic Zone[J].BSSA,88(2):564-580.
- Brehm D J,Braile L W.1999.Intermediate-term earthquake prediction using the modified time-to-failure method in southern California[J].BSSA,89(1):275-293.
- Bufe C G,Varnes D J.1993.Predictive modeling of the seismic cycle of the greater San Francisco Bay region [J].JGR,98(B6):9871-9883.
- Gutenberg B,Richter C F.1956.Earthquake magnitude,intensity,energy and acceleration[J].BSSA,46(2):105-145.
- Jaumé S C,Sykes L R.1999.Evolving towards a critical point:A review of accelerating seismic moment/energy release prior to large and great earthquake[J].Pure Appl Geophys,155(2-4):279-305.
- Jiang C S,Wu Z L.2006.Benioff strain release before earthquakes in China:accelerating or not? [J].Pure Appl Geophys,163(9):1965-1976,doi:10.1007/s00024-006-0107-1.
- Knopoff L,Levshina T,Keilis-Borok V I,et al.1996.Increased long-range intermediate magnitude earthquake activity prior to strong earthquakes in California[J].JGR,101(B3):5779-5796.
- Mignan A,Giovambattista R D.2008.Relationship between accelerating seismicity and quiescence,two precursors to large earthquakes[J].Geophys Res Lett,35,L15306,doi:10.1029/2008GL035024.
- Sykes L R,Jaumé S C.1990.Seismic activity on neighboring faults as a long term precursor to large earthquakes in the San Fancisco Bay area[J].Nature,348:595-599.
- Varnes D J.1989.Predicting earthquakes by analyzing accelerating precursory seismic activity[J].Pure Appl Geophys,130(4):661-686.
- Wang Y C,Yin C,Mora P,et al.2004.Spatio-temporal scanning and statistical test of the accelerating moment release(AMR)model using Australian earthquake data[J].Pure Appl Geophys,161(11-12):2281-2293.