近年来利用背景噪声研究地下结构已经成为一个热点。Aki(1957)提出地震动信号的空间相关能够得到一个用来研究地震序列相速度的贝塞尔函数; Claerbout(1968)推测可通过对两点记录到的散射地震背景噪声进行互相关计算提取脉冲响应,即通过互相关计算提取格林函数。该猜想最早在日震学领域得到证实和应用,通过对太阳表面噪声进行互相关计算得到太阳外层三维流速度结构(Rickett,Clarebout,1999)。随着计算技术的提高和这一理论的不断发展,直到2005年利用地震背景噪声提取台站格林函数的尝试才取得成功(Shapiro et al,2005)。随后,这种方法在地震学领域得到迅速发展,应用到面波层析成像(Shapiro et al,2005; Sabra et al,2005; Yao et al,2006; )、火山监测(Sabra et al,2006; Brenguier et al,2007)、地震波速变化监测(李军等,2009; 刘志坤,黄金莉,2010)、背景噪声源分析(郑定昌等,2011)以及地壳介质的衰减测量分析(Prieto et al,2008,2009; Lin et al,2011)等方面。

这些研究在使用互相关计算提取格林函数时,为了去除地震信号、仪器故障引起的畸变信号以及记录台站附近干扰对互相关计算结果的影响,对记录的数据做了“one-bit”、谱白化或滑动绝对平均处理(Campillo,Paul,2003; Bensen et al,2007; 房立华,吴建平,2009),但是,通过“one-bit”或谱白化处理得到的格林函数只保留了相位信息,丢失了幅值信息(Larose et al,2007),而幅值信息恰恰是反映地下介质的重要参数; 滑动绝对平均方法虽然可以保留部分幅值信息,但应用该方法时滑动时窗长度不易选取,且保留幅值信息的多少也不易确定。

另有学者研究表明利用反褶积运算提取含有幅值信息的格林函数已成为可能(Snieder,Safak,2006; Kohler et al,2007),Prieto等(2008,2009)将这一方法运用到了地震背景噪声研究中,从中提取出了具有相对幅值信息的格林函数,并利用获得的幅值衰减特性进行了地壳的非弹性研究。需要指出的是,在Prieto等(2008,2009)的研究中以记录到每两小时的非重叠的背景噪声原始数据作为对象提取格林函数,计算前对数据进行筛选,若数据记录有天然地震(尤其是远震)或尖峰等干扰,则剔除该段数据,不进行格林函数提取计算。显然该方法在地震频发(如云南地区)和记录数据质量不高的台网区域并不适用。本文通过对该方法的研究,设计出一种可自动剔除天然地震和尖峰干扰的方法,利用反褶积提取含有幅值信息的高信噪比格林函数。

已有研究推导证明,与互相关计算类似,通过对两个台站记录到的长时间地震背景噪声数据进行反褶积计算,可以提取台站间的格林函数(Vasconcelos,Snieder,2008a,2008b; Prieto et al,2009)。 A、B两点数据记录u_A(t), u_B(t)的反褶积计算在频率域内可表示为

D_AB(ω)=(u_A(ω))/(u_B(ω))=(u_A(ω)u_B^*(ω))/(u_B(ω)u_B^*(ω))

=(u_A(ω)u_B^*(ω))/(|u_B(ω)|²),(1)

式中,由于分母项|u_B(ω)|²可能会出现值为0的情况,造成反褶积计算的不稳定,为了平衡这一问题,可将(1)改写为

D_AB(ω)=(u_A(ω)u_B^*(ω))/(|u_B(ω)|²+ε).(2)

式中,参数ε一般按u_B(ω)平均功率谱的一定比例给出。

笔者利用多窗谱分析方法将背景噪声数据转换到频域后,再做反褶积计算提取格林函数。多窗谱分析是Thomson(1982)在经典的谱分析的基础上提出的,与经典的直接法只有一个窗函数不同,多窗谱分析使用的窗函数是一组相互正交的离散椭球序列,也叫Slepian窗。多窗谱分析计算是对各窗函数下的直接谱求平均所得,该方法得到的谱具有方差较小的优点,且更接近真实的谱。

对于采样率为τ,数据长度为T=Nτ的数据记录u(nτ)的多窗谱分析(Thomson,1982; Park et al,1987)估算,可写为

u^k(ω)=∑^n-1_n=0u(nτ)w^k_ne^i2πωnτ(3)

式中,{w^k_n}^N-1_n=0是k=0,1,2,3,…,K-1阶Slepian数据窗,其中K为窗函数的最大阶数,与时间带宽积p=NW(N数据长度,W为带宽)具有K=2p-1的关系。

将式(3)代入式(2),即得到多窗谱反褶积计算公式:

D_AB(ω)=(u_A(ω)u_B^*(ω))/(|u_B(ω)|²+ε)

=(∑^K-1_k=0u^k_A(ω)(u^k_B(ω))^*)/((∑^K-1_k=0u^k_B(ω)(u^k_B(ω))^*)+ε).(4)

为了得到高信噪比的格林函数,需要在反褶积计算前进行数据预处理。其预处理步骤包括去仪器响应、去均值、去趋势项和带通滤波等,这与互相关计算中标准化的处理步骤类似(Bensen et al,2007)。在进一步的预处理中,常用的“one-bit”处理方法不能满足去除干扰信号的同时又保留振幅信息的要求,而时间域归一化滑动绝对平均方法,虽然可以部分地保留振幅信息,且能够很好地保留长周期的信号,但其滑动时间窗长度的选取不易把握,且其能够保留的振幅信息多少亦难以确定(Bensen et al,2007; 房立华,吴建平,2009)。因此本文设计一种算法,该算法能够在去除地震信号和仪器故障引起的信号畸变等一些干扰的同时,又尽可能完整的保留下幅值信息。

对于N点背景噪声记录数据u(nτ),进行如下处理:

(1)计算背景噪声u(nτ)的均方根:

D_rms=(1/N∑^N_n=1u(nτ)^*)^1/2;(5)

(2)找寻出数据中振幅值大于均方根(D_rms)M倍(M一般取2)的记录点u(Idτ), 并给出最大幅值u_imax:

|u(Idτ)|>M*D_rms,(6)

u_imax=max(|u(nτ)|);

(3)将数据序列u(Idτ)除以u_imax后, 与均方根D_rms相乘, 实现最大值均一化:

u(Idτ)'=(u(Idτ))/(u_imax)*D_rms;(7)

(4)将u(Idτ)'序列替换u(nτ)中对应的记录值, 即可得到新的时间序列u(nτ)';

(5)重复(1)～(4)步骤, 对新的时间序列u(nτ)'做最大值均一化处理,直到数据记录达到了消除干扰的目的。

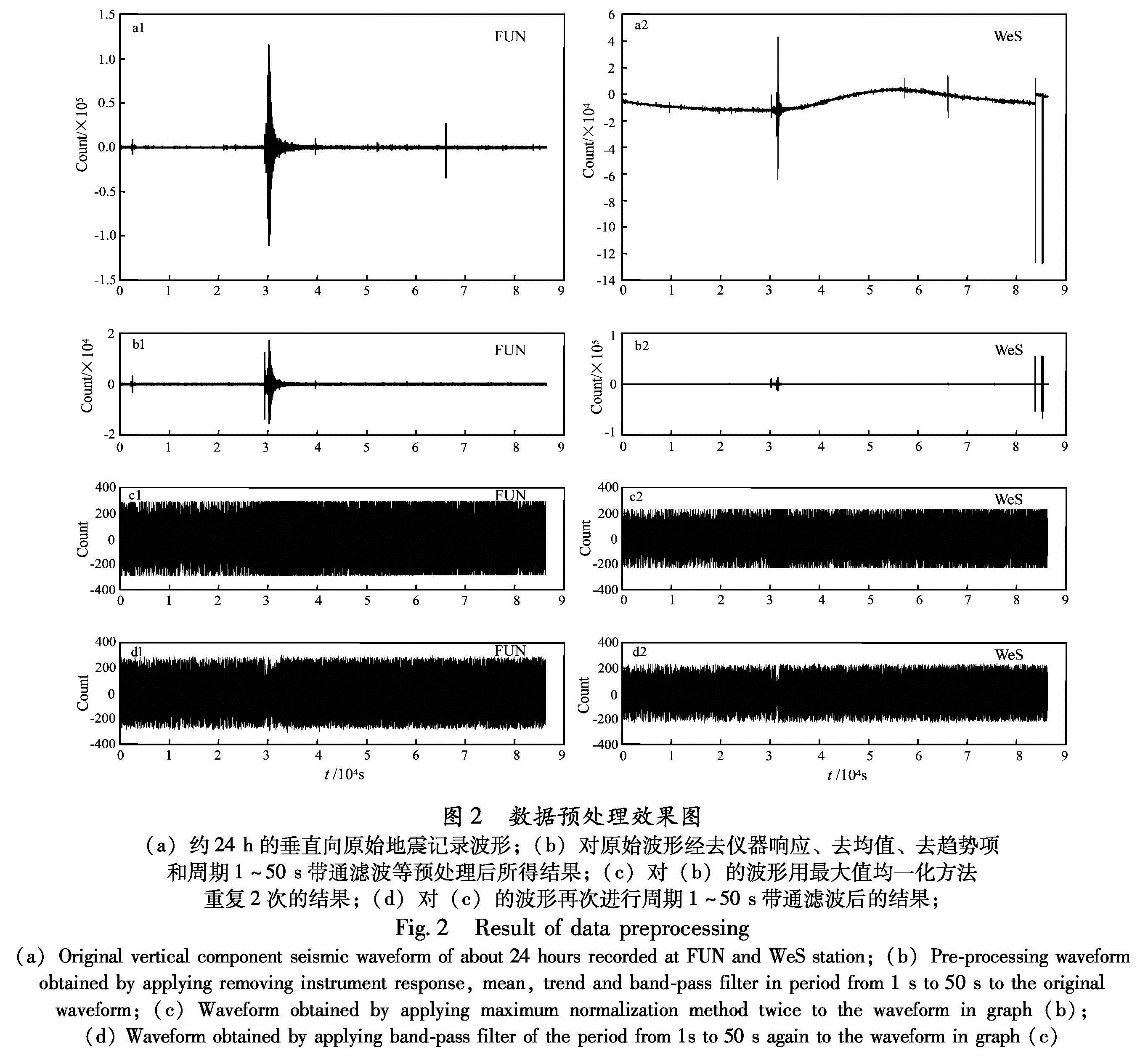
我们将上述处理方法定义为多次最大值均一化方法。发现一般重复2～3次,即可消除地震信号干扰和尖峰干扰。我们选取FUN(富宁,图1空心五角星标注)、WeS(文山,图1中实心五角星标注)所记录到的连续数据,运用最大均一化方法对单台站数据预处理,图2中,a1、a2分别为FUN台2008年6月14日、WeS台2008年6月23日垂直向约24 h原始地震记录波形,b1、b2分别为经FUN和WeS台去仪器响应、去均值、去趋势项和周期1～50 s带通滤波等前期预处理后所得结果,c1、c2分别为对b1、b2的结果使用最大值均一化方法重复2次所得结果。经处理后,c1与b1、c2与b2的数值重合率分别为97.54%、98.71%。d1、d2分别是对c1、c2数据再次进行周期1～50 s带通滤波后的结果,表明最大值均一化方法有效地消除了a1中远震信号和a2中小震及畸变信号干扰。

图1 云南测震台网分布图
Fig.1 Distribution of stations in Yunnan digital seismic network

图2 数据预处理效果图(a)约24 h的垂直向原始地震记录波形;(b)对原始波形经去仪器响应、去均值、去趋势项和周期1～50 s带通滤波等预处理后所得结果;(c)对(b)的波形用最大值均一化方法重复2次的结果;(d)对(c)的波形再次进行周期1～50 s带通滤波后的结果;
Fig.2 Result of data preprocessing(a)Original vertical component seismic waveform of about 24 hours recorded at FUN and WeS station;(b)Pre-processing waveform obtained by applying removing instrument response, mean, trend and band-pass filter in period from 1 s to 50 s to the original waveform;(c)Waveform obtained by applying maximum normalization method twice to the waveform in graph(b); (d)Waveform obtained by applying band-pass filter of the period from 1s to 50 s again to the waveform in graph(c)

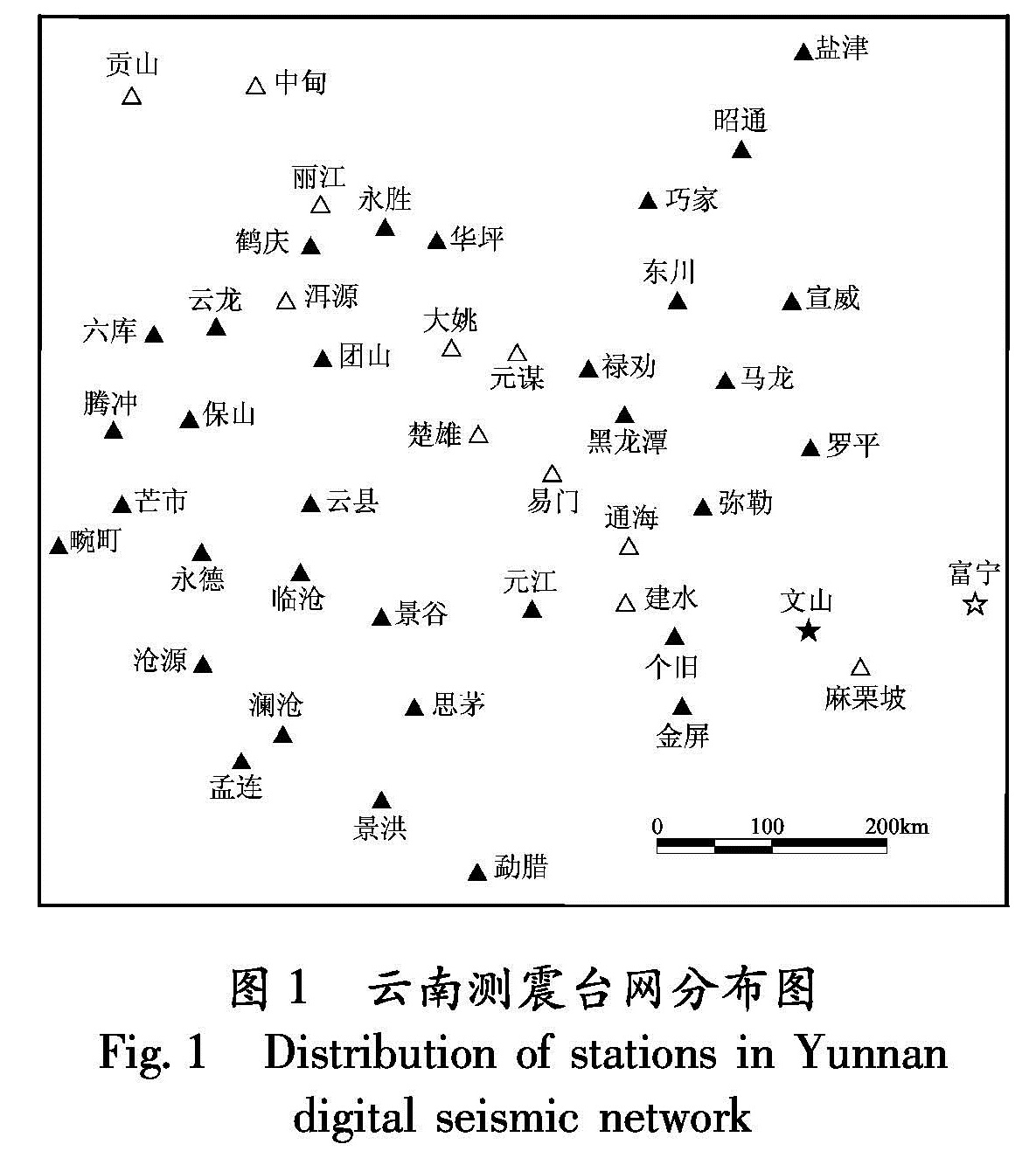
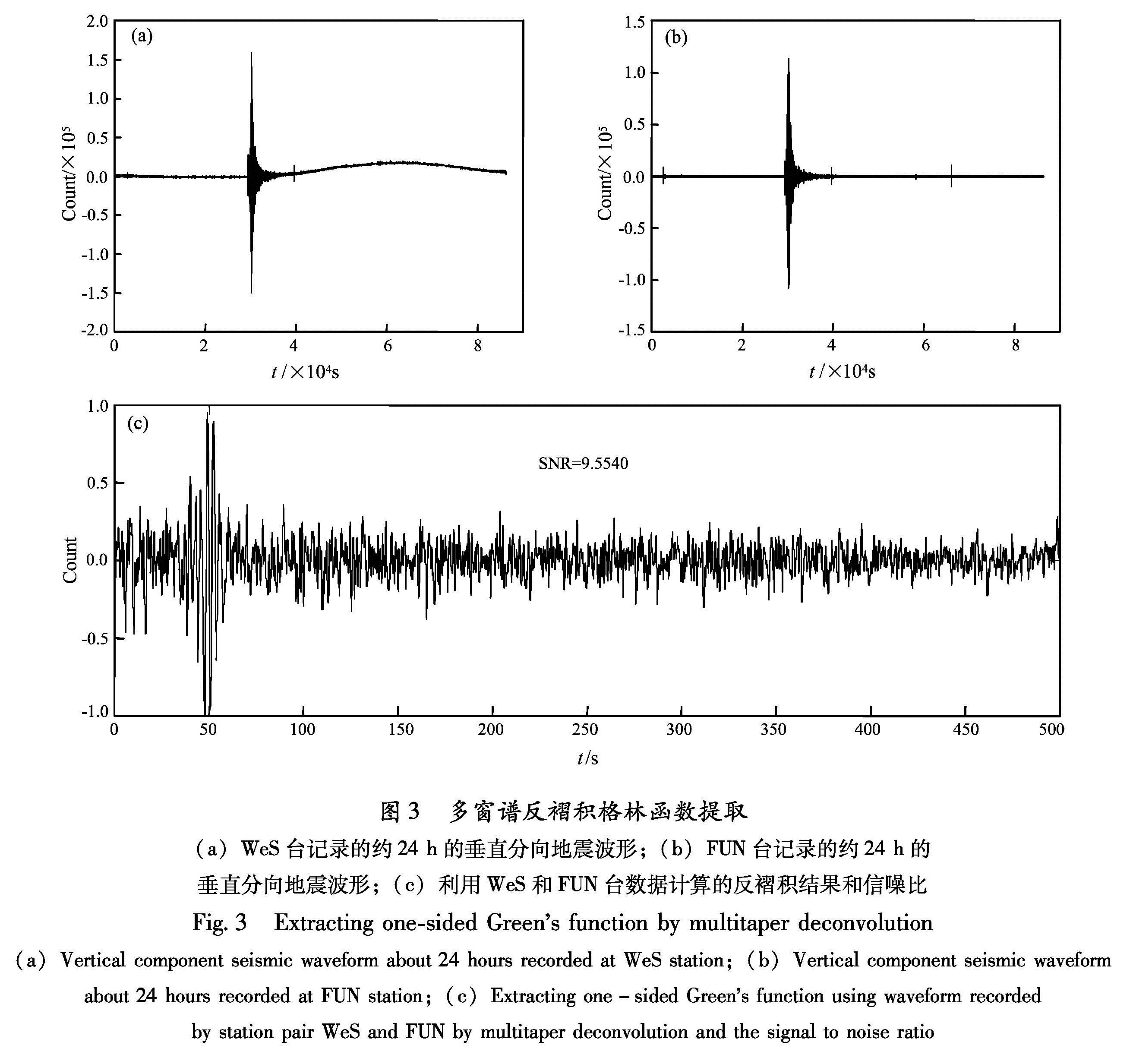
为了验证本文所述反褶积提取格林函数的有效性,选取2008年6月14日WeS(图3a)、FUN(图3b)约24 h记录的地震波形进行反褶积计算提取格林函数,台间距约142 km。通过数据预处理将记录到的远震干扰信号进行去除,处理过程中选用周期1～50 s带宽进行了带通滤波,重复2次使用最大值均一化算法; 在对干扰信号有效去除的基础上,利用(4)式所示的多窗谱反褶积方法提取格林函数,计算时时间带宽积p=3.0,K=5,ε取WeS台站记录数据平均功率的1‰,选用非重叠的2 h时窗进行滑动计算,一天计算出12个结果,对其叠加得到该日单边格林函数,并进行了归一化处理如图3c所示。计算该格林函数信噪比(SNR)为9.5540。

图3 多窗谱反褶积格林函数提取(a)WeS台记录的约24 h的垂直分向地震波形;(b)FUN台记录的约24 h的垂直分向地震波形;(c)利用WeS和FUN台数据计算的反褶积结果和信噪比
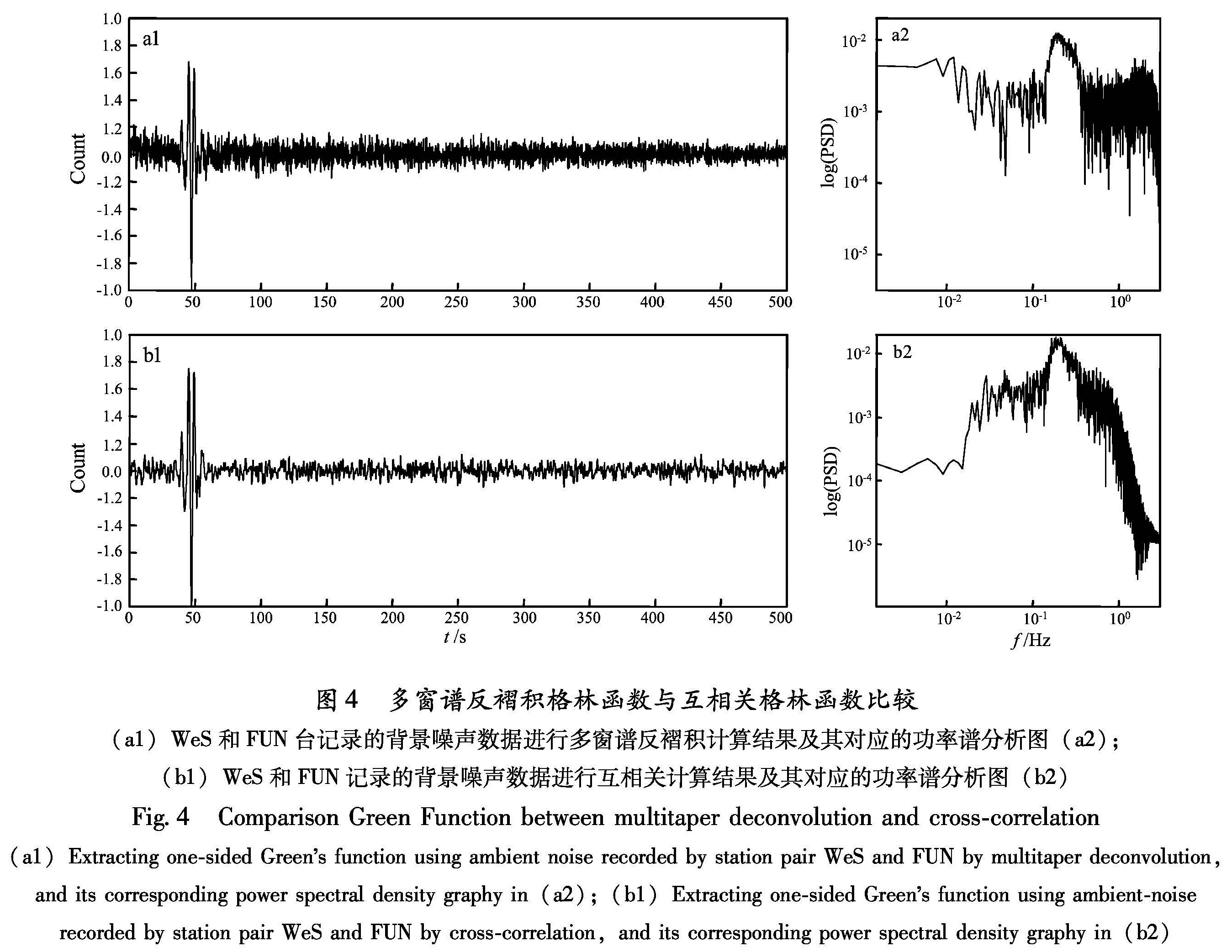
Fig.3 Extracting one-sided Green's function by multitaper deconvolution (a)Vertical component seismic waveform about 24 hours recorded at WeS station;(b)Vertical component seismic waveform about 24 hours recorded at FUN station;(c)Extracting one-sided Green's function using waveform recorded by station pair WeS and FUN by multitaper deconvolution and the signal to noise ratio

同时,我们又分别利用多窗谱反褶积和互相关两种算法对2008年7月29日WeS、FUN记录到的1天的背景噪声数据进行了格林函数计算,结果如图4a1、b1所示。对其进行功率谱分析得到图4a2、b2,表明反褶积提取的格林函数图4a1较互相关提取的格林函数图4b1具有更宽的频带响应,蕴含了更丰富的信息。

地球作为一个非弹性体,地震波在其内部传播的过程中,随着传播距离的增加,必然造成能量的衰减,衰减有两个因素:几何衰减和阻尼衰减(胡聿贤,1999)。背景噪声场由于其存在多重散射和固有的衰减,从背景噪声中提取的格林

图4 多窗谱反褶积格林函数与互相关格林函数比较(a1)WeS和FUN台记录的背景噪声数据进行多窗谱反褶积计算结果及其对应的功率谱分析图(a2); (b1)WeS和FUN记录的背景噪声数据进行互相关计算结果及其对应的功率谱分析图(b2)
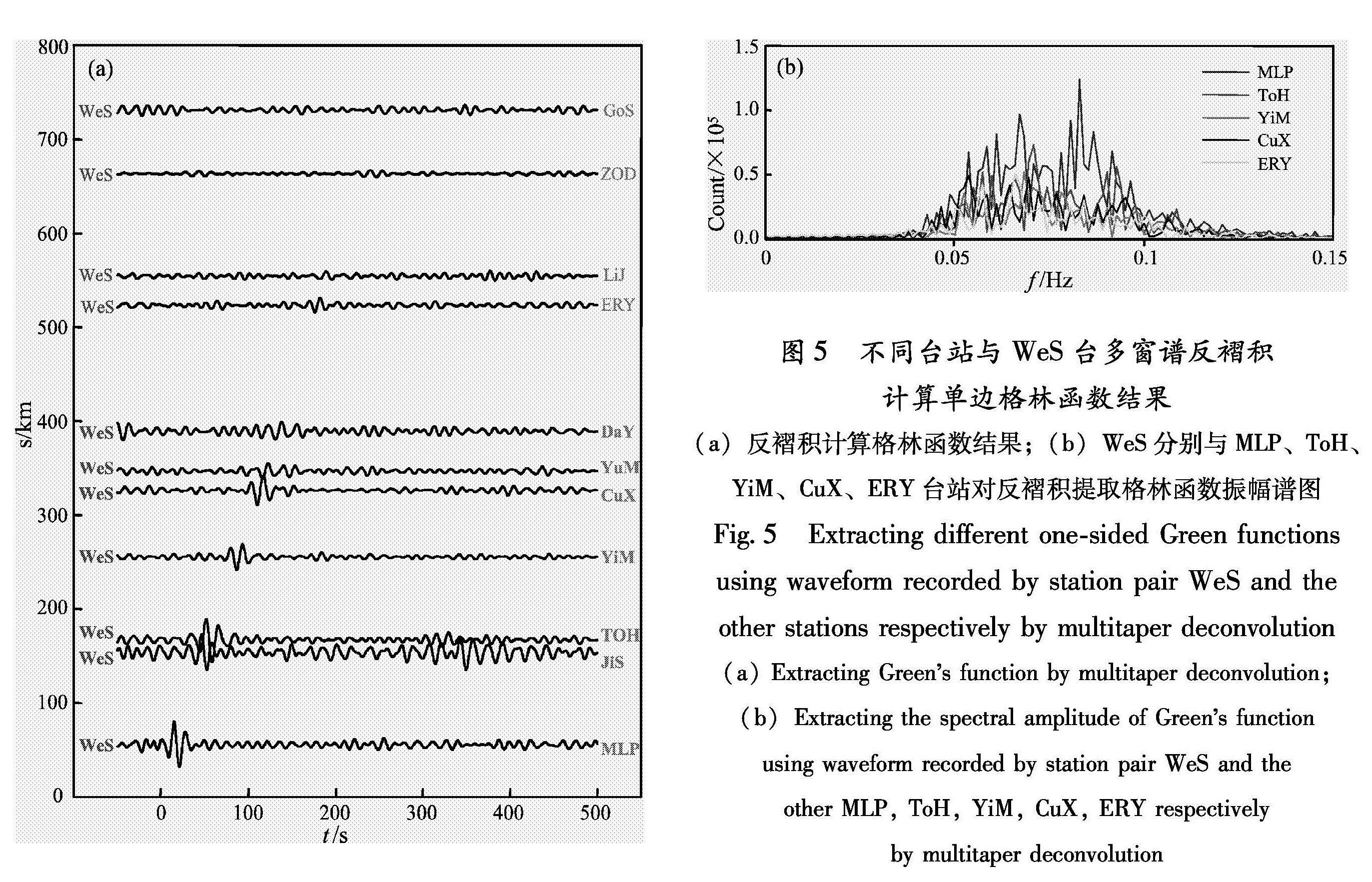
Fig.4 Comparison Green Function between multitaper deconvolution and cross-correlation(a1)Extracting one-sided Green's function using ambient noise recorded by station pair WeS and FUN by multitaper deconvolution,and its corresponding power spectral density graphy in(a2);(b1)Extracting one-sided Green's function using ambient-noise recorded by station pair WeS and FUN by cross-correlation,and its corresponding power spectral density graphy in(b2)

图5 不同台站与WeS台多窗谱反褶积计算单边格林函数结果(a)反褶积计算格林函数结果;(b)WeS分别与MLP、ToH、YiM、CuX、ERY台站对反褶积提取格林函数振幅谱图
Fig.5 Extracting different one-sided Green functions using waveform recorded by station pair WeS and the other stations respectively by multitaper deconvolution(a)Extracting Green's function by multitaper deconvolution; (b)Extracting the spectral amplitude of Green's function using waveform recorded by station pair WeS and the other MLP, ToH, YiM, CuX, ERY respectively by multitaper deconvolution

为了表明经过最大值均一化方法处理后的背景噪声数据进行多窗谱反褶积计算提取的格林函数保留了幅值信息。笔者利用WeS台(图1中实五角星标注)与其它11个台站(图1中空心三角形标注),在2009年1～5月记录到的背景噪声数据进行反褶积提取格林函数,计算前对各个台站记录的数据进行了灵敏度校正,结果如图5所示。图5a为所进取的11个不同台站与WeS台反褶积提取的5个月格林函数叠加结果,且随台间距增大,自下而上排列图示,图5b则为对MLP、ToH、YiM、CuX、ERY台记录的数据提取到的格林函数进行振幅谱分析的图示。结果表明随着台间距的增大其格林函数的幅值具有减小的趋势,如台间距最小的WeS-MLP格林函数幅值最大,随台间距的加大WeS-ZOD、WeS-GoS幅值已经衰减到很弱,同时也存在幅值随台间距增加出现衰减异常的情况,如台间距较大的WeS-CuX与台间距较小的WeS-YiM的格林函数幅值相当,这可能是由于CuX台位于楚雄盆地内,盆地对其具有放大效应所致(Prieto et al,2008)。

本文针对云南这一地震频发区域,采用多窗谱反褶积计算方法从背景噪声中提取了含有相对幅值、信噪比较高的格林函数,其提取的格林函数与互相关提取格林函数对比表明反褶积提取的格林函数蕴含有更丰富的信息内容。我们在数据预处理的步骤过程中,设计了一种可以有效消除地震背景噪声中天然地震干扰信号和仪器畸变信号的最大值均一化方法,利用该方法预处理后的背景噪声数据能够很好的保留绝大部分的振幅信息。