基金项目:地震科学联合基金(C08036)和地震科技星火计划项目(XH12017Y)联合资助.
(1.同济大学 海洋与地球科学学院,上海 200092; 2.上海市地震局,上海200062)
(1.School of Ocean and Earth Science,Tongji University,Shanghai 200092,China)(2.Earthquake Administration of Shanghai Municipality,Shanghai 200062,China)
borehole deformation; deformation observation; wavelet transform; background noise; Sheshan Station in Shanghai
备注
基金项目:地震科学联合基金(C08036)和地震科技星火计划项目(XH12017Y)联合资助.
对上海佘山钻孔形变观测资料正常的背景噪声进行初步分析并定量刻画其正常信息场的变化特征。结果 显示:上海佘山形变观测资料的小波变换细节部分不同尺度包含着不同的信号成分,通过研究形变观测资料小波变换各尺度信号的非震异常特征变化,可能会捕捉到与地震孕育过程有关的前兆异常信息。
We analyze characteristics of the normal background noise of borehole deformation observation data recorded at Sheshan Station in Shanghai,and quantitative characterize variation characteristics of their normal information field.The results show that the different scales of the wavelet transform detail parts of deformation observation data contain different signal components.Through studying the non-seismic anomaly characteristics change of different signal scale of wavelet transform,we may obtain precursor information of the earthquake preparation process.
引言
由于地震发生于地壳深部,而地震观测只能在地球表面或近地表开展,一方面,大多数地震的信号都非常小,要求地震监测系统的接收灵敏度必须很高; 另一方面,地球表面或近地表不可避免地受到各种人为因素的干扰; 同时各个台站由于本身地质构造的差异性,其背景噪音也各有其独特的特征。因此,这就产生一个疑问,基于地表观测推断的地球深部物质组成、特性、环境、地震孕育、发生、发展的物理机理和物理过程是否真正代表地下实际?目前上海地表观测资料,能否为地震预报、震灾预防和地震预警以及地震科学研究提供可靠的观测资料,从而能更广泛、更深入地了解地球内部的动力作用过程?
目前,傅里叶变换和小波变换被广泛地应用在地球物理资料的处理和分析中,成为最基本的一种分析手段。傅立叶变换的基本思想是将信号分解成一系列不同频率的连续正弦波的叠加,但变换时会丢失时间信息,无法判断一个特定信号何时发生; 小波理论在时间域和频率域都达到较高的分辨率,被称为“数学显微镜”,在数值信号处理领域得到广泛应用并得到了大量有益的结果。武安绪等(2007)利用二进正交离散小波对数字形变资料趋势异常进行了分析探讨; 敬少群等(2002)利用小波变换理论对地下水观测资料进行应用分析; 张永志等(1998,1999)利用小波变换进行重力异常、大面积形变测量和定点形变测量资料中地震异常分析研究; 宋治平等(2003)基于小波变换理论,提出了应用小波分析方法识别、消除数字化资料的干扰、提取不同频率信息的方法; 张燕等(2004)利用小波变换的时频分析和奇异性检测特性,对几次地震前的形变时间序列资料(定点潮汐形变观测、GPS 观测)作小波变换,结果发现不同的地震异常出现的时间不一样,这些同时出现在多个台站或观测站的同频段的异常信号可能是地震前兆。
本文基于小波变换技术,对上海佘山钻孔形变观测资料的正常背景噪声进行初步分析,定量刻画其正常信息场的变化特征,为利用上海佘山形变观测资料进行地震预测分析等研究提供可靠资料,进而为识别地震异常信息、揭示地壳应力应变的变化过程研究,提供更加客观背景特征参考值。
1 小波变换理论
设Ψ(t)∈L2(R)函数, 并且满足条件
∫+∞∫-∞Ψ(t)dt=0,(1)
定义
Ψa,b(t)=a1/2Ψ((t-b)/a).(2)
式中,a,b∈R,a≠0,Ψ(t)为小波基函数或母小波函数,a为尺度参数,b为平移参数。
对于任意函数f(t)∈L2的连续小波变换为
Wf(a,b)=∫+∞∫-∞f(t)Ψa,b(t)dt, a>0.(3)
式中,小波变换的基函数Ψa,b(t)是窗函数Ψ(t)进行时间平移和尺度伸缩的结果。尺度参数a的变化可以改变窗口的大小,若a>1,基函数相当于将窗函数拉伸,使窗口的时宽增大,其频谱变窄并朝低频方向移动; 若a<1,基函数相当于将窗函数压缩,使窗函数缩小,其频谱展宽并向高频方向移动。大尺度参数对应低频端,频率分辨率高、时间分辨率低; 相反,小尺度参数对应高频端,频率分辨率低、时间分辨率高,这就是小波变换的多分辨特性。参数b起时移作用,b的变化只影响时频窗的中心点在时间轴上的位置,而对时频窗的形状无影响; 随着a的增大,时频窗的中心频率降低,时间宽度增大,但时频窗的面积保持不变,a、b的联合作用可使时频窗覆盖整个相空间。式(3)相当于用一系列不同宽度的时窗去分析f(t)在b时刻附近的频率成分,由于Ψ(t)是局域化的,因而小波变换同时具有良好的频域局部性和时域局部性,即可以实现对信号的“变焦”分析(万永革,2007)。
2 资料和计算方案
选取上海佘山台“十五”期间建设的钻孔应变和钻孔倾斜无震期间(2010年11月1~30日)的数据作为研究资料,分别选取该时段内应变数据和倾斜数据的整点值和分钟值进行分析,其中钻孔应变为四分量应变仪,钻孔倾斜为二分量倾斜仪。在这1个月的数据中,应变记录连续可靠,倾斜记录的分钟值中漏记9个数据,对这9个缺数进行内插预处理,实现观测数据的连续和可靠。
由于固体潮等影响,形变观测数据由一系列不同频率的周期成分和背景噪声叠加组成,周期性较明显。因此,本文利用小波分析时选用正则性较好的daubec-Hies小波进行分析,并结合李杰等(2005)给出的方法对佘山形变观测数据噪声和信号进行定量识别,分析形变资料的噪音动态特征。由于篇幅关系和结果的一致性,只给出应变仪东西向分量观测资料时间序列图。
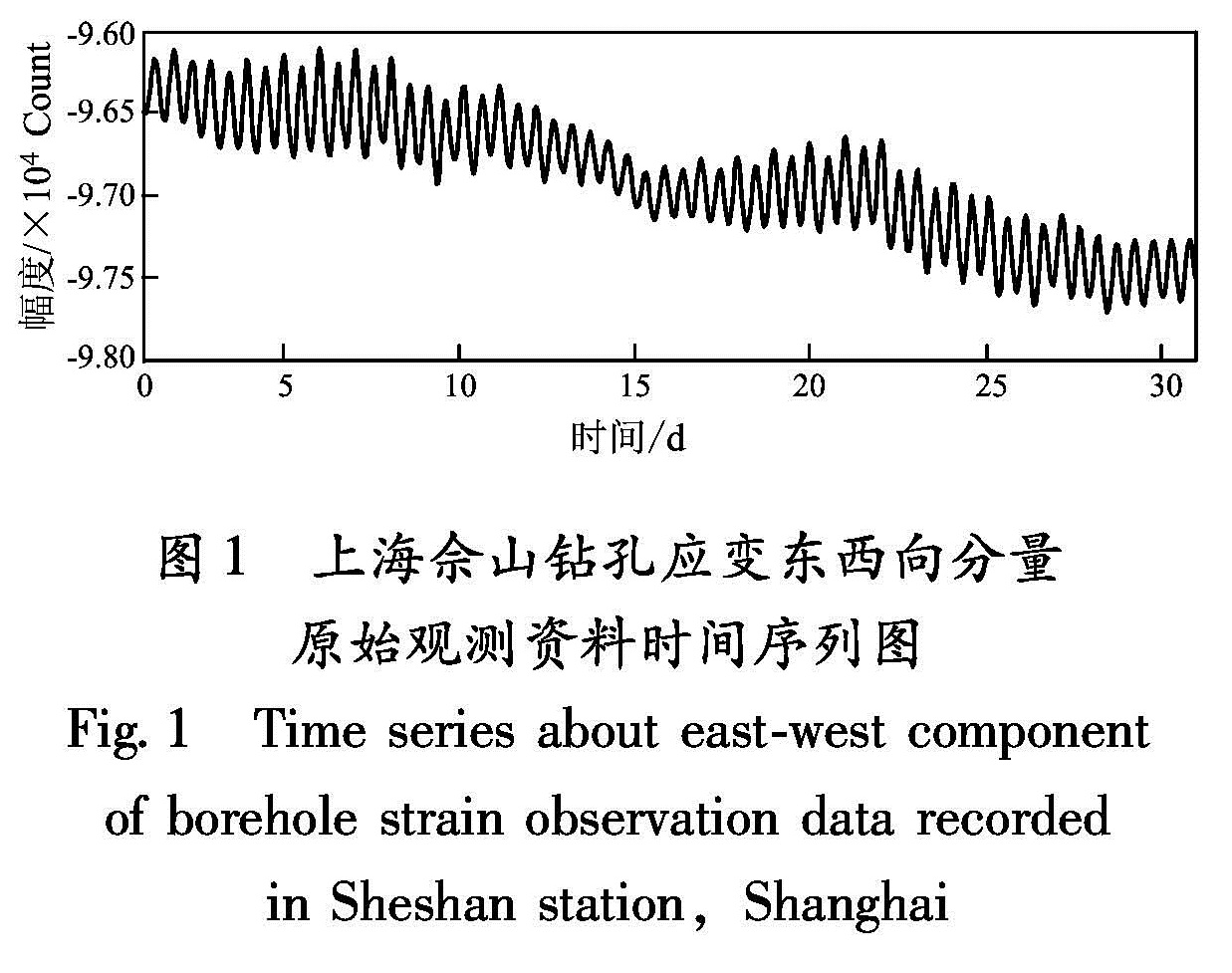
3 佘山形变观测资料小波分解
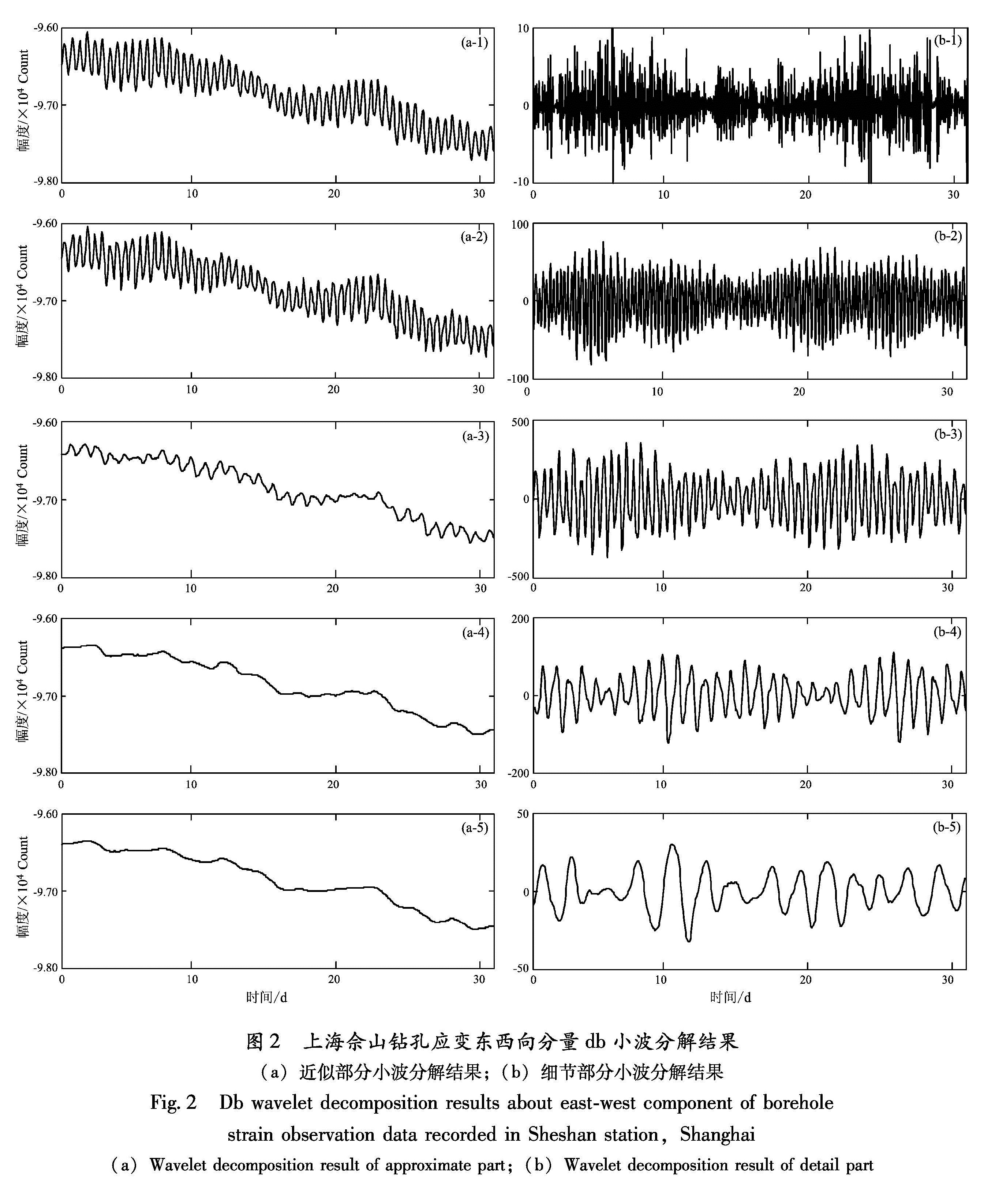
采用2010年11月上海佘山台应变观测资料和倾斜观测资料的整点值进行小波变换分析。图1给出了应变仪东西向分量原始观测资料时间序列图; 图2为东西向分量的小波分析近似部分与细节部分的分解曲线。比较图1和图2,可见低频信息主要反映趋势变化过程,而高频信息反映的是短期变化过程。图2a给出了不同频率范围的近似部分,反映出整体变化趋势,而小波变换分解出的细节部分(图2b)主要反映了固体潮汐的1/4日波、半日波、日波、半月波的高频变化信息。因此,应用小波变换方法对数字化前兆资料中的不同频率的潮汐波信息可进行识别。在不同频率的信息识别基础上,也可以应用小波变换对不同频率的信息进行分离。在实际工作中,可以通过从分离出的不同频率固体潮异常中,识别地震前兆信息。本文只给出应变东西向分量分解结果,其它分量以及倾斜观测资料也具有同样的特征。
4 佘山形变观测数据背景噪声和信号的定量分析
如果观测数据x(t)的各阶统计量不随时间的变化而改变,则称x(t)为平稳信号; 如果观测数据x(t)某阶统计量随时间改变,则称x(t)为非平稳信号; 如果观测数据x(t)的二阶或高阶统计量不随时间的变化而改变,则称x(t)为二阶或高阶平稳信号,其自相关函数(张贤达,保铮,1995)表示为
x(τ)=(1/(n-τ)∑n-τt=1{[x(t)-μ][x(t+τ)-μ]})/(1/n∑nt=1[x(t)-μ]2).(4)
其中,n为观测资料长度,τ为延迟因子,μ为观测数据均值。为定量刻画式(4)中除τ=0以外的随机噪声、循环平稳信号和非平稳信号自相关函数x(τ)的差异特征,本文采用李杰等(2005)给出的用二次项式方法拟合信号自相关函数,具体表达式为
图2 上海佘山钻孔应变东西向分量db小波分解结果(a)近似部分小波分解结果;(b)细节部分小波分解结果
Fig.2 Db wavelet decomposition results about east-west component of borehole strain observation data recorded in Sheshan station,Shanghai (a)Wavelet decomposition result of approximate part;(b)Wavelet decomposition result of detail partx(τ)≈aτ2+bτ+c.(5)
式中,a是用来描述自相关函数非线性衰减特性的因子,b是用来描述自相关函数线性衰减特性的因子,c是用来描述信号和噪声的识别因子。所得二次项拟合系数显示(李杰等,2005):纯白噪声序列、循环平稳序列和非平稳序列相比,各自具有不同的典型特征,白噪声的一次项系数、常数项和识别误差最小; 循环平稳信号的常数项值最大; 非平稳信号的二次项系数、一次项系数和识别误差最大。钻孔形变观测数据主要由纯白噪声、平稳信号和非平稳信号这三种信号构成,其中非平稳信号里可能包含着地壳形变信息,是我们所要识别的信号。
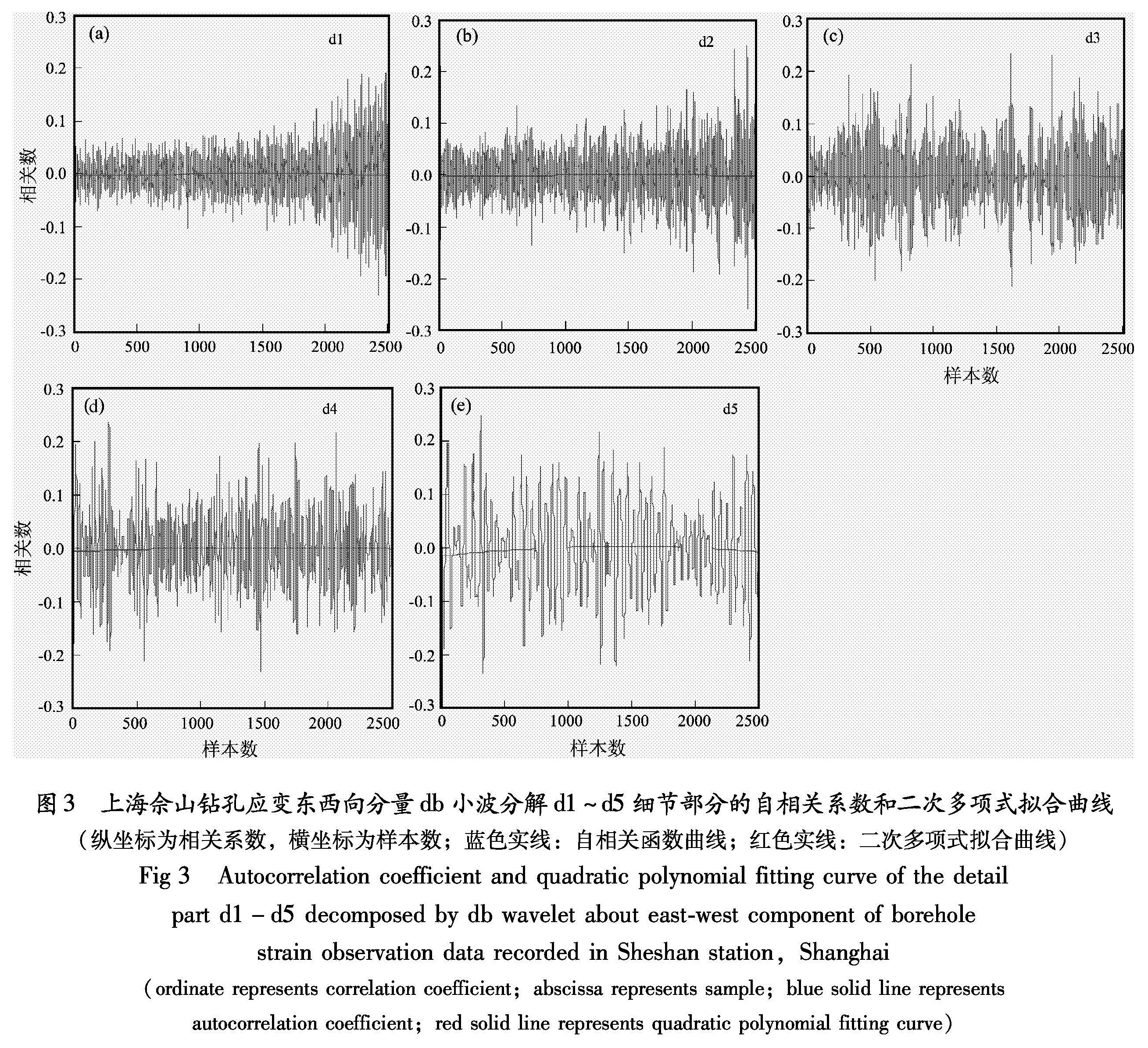
对观测数据进行db小波分解后,将分解所得的各细节信号时间序列利用式(4)进行自相关分
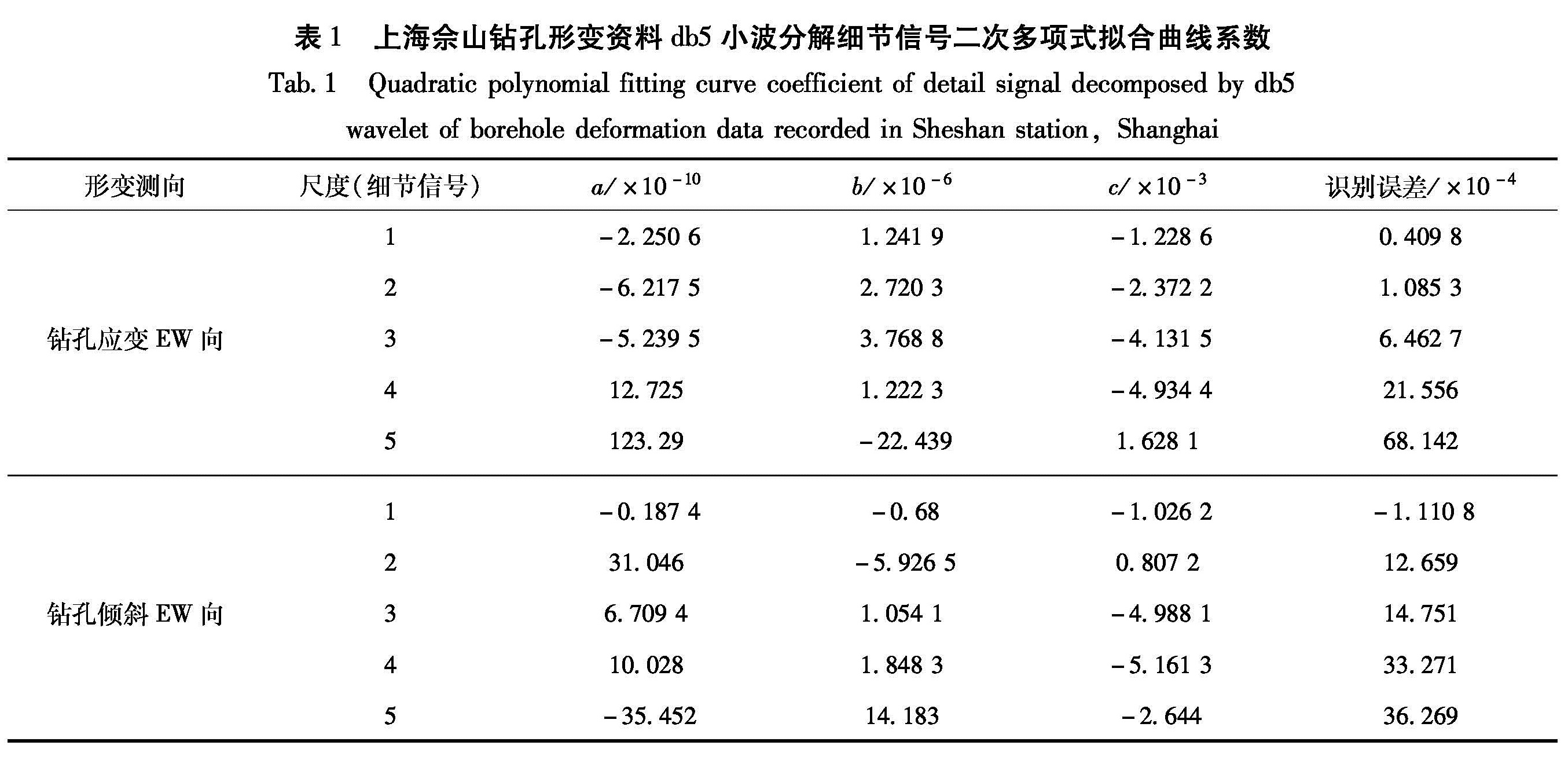
析,分析结果见图3中的蓝色实线。再利用式(5)对自相关系数进行二次项拟合得到各二次项拟合曲线,见图3中的红色实线,同时把二次多项式拟合系数计算结果列于表1,最后根据上述结论对佘山形变观测和倾斜观测数据的背景噪声和信号进行定量分析,以期得到非平稳信号的动态变化特征,具体结果如表1所示,表中a,b,c分别代表二次项系数、一次项系数和常数。
(1)尺度1、2的细节信号识别误差最小,而尺度1的一次项和常数项基本较小,尺度2没有明显规律,表明尺度1基本由纯白噪声构成,而尺度2中除了噪声外,还包含着非平稳信号。
(2)尺度3、4的细节信号常数项值较大,表明尺度3、4中主要以平稳信号为主,主要反应了固体潮汐的稳定周期变化信息。
(3)从表1中可以看出,尺度5的二次项系
图3 上海佘山钻孔应变东西向分量db小波分解d1~d5细节部分的自相关系数和二次多项式拟合曲线(纵坐标为相关系数,横坐标为样本数; 蓝色实线:自相关函数曲线; 红色实线:二次多项式拟合曲线)
Fig 3 Autocorrelation coefficient and quadratic polynomial fitting curve of the detail part d1-d5 decomposed by db wavelet about east-west component of borehole strain observation data recorded in Sheshan station,Shanghai (ordinate represents correlation coefficient; abscissa represents sample; blue solid line represents autocorrelation coefficient; red solid line represents quadratic polynomial fitting curve)表1 上海佘山钻孔形变资料db5小波分解细节信号二次多项式拟合曲线系数
Tab.1 Quadratic polynomial fitting curve coefficient of detail signal decomposed by db5 wavelet of borehole deformation data recorded in Sheshan station,Shanghai数、一次项系数和识别误差基本上都远远大于其它尺度细节信号相应系数,对比非平稳序列的典型特征,表明尺度5中具有非常显著的非平稳序列典型特征,即佘山形变观测资料中地壳形变信息可能包含在该尺度内,在日常的分析中应特别注意。
5 结论和讨论
小波分析在处理地球物理信息场时有其独特的优越性,可以给出信号在不同尺度下的近似和细节部分,分析不同频率范围的正常变化背景。在进行地震前兆异常分析时可以根据不同尺度的近似和细节部分的正常背景作为依据,判断观测数据是否存在着长期和短期异常。
从佘山形变观测资料db小波分解结果看,近似部分反应了信号的长趋势变化,主要为仪器的零漂,从小波变换细节部分分解出的不同层数得到固体潮汐的1/4日波、半日波、日波、半月波的高频变化信息。因此,应用小波变换方法对数字化前兆资料中的不同频率的潮汐波信息可进行识别,可以针对不同频率的细节部分进行分析,能清晰地辨别固体潮畸变信息成分,从而能更有利于对地震前兆异常或者干扰的分析。
对上海佘山地震台形变观测数据背景噪声和信号进行定量分析,发现尺度1基本由纯白噪声构成,而尺度2中除了噪声外,还包含着非平稳信号; 对于尺度3、4,细节信号常数项值较大,以平稳信号为主; 尺度5中非平稳信号占显著成分,可能包含着地壳形变信息,是我们所要识别和关注的信号成分。
对形变观测资料进行分析的目的是从信号中得到地壳形变等有价值前兆异常现象,而信号中的白噪声以及客观存在的平稳信号等对于地震前兆异常分析来说,是一定的干扰,本文从信号的特征出发,通过小波分解以及后续处理,从信号中分离出非平稳信号,最大限度地使观测不受其它已知客观环境的干扰。非平稳信号中包含着的地壳形变信息如何进一步分离以及如何提高分辨,需要进一步的研究。
综上所述,本文基于小波变换方法,对上海佘山钻孔形变观测资料正常的背景噪声进行初步分析并定量地刻画了其正常信息场的变化特征,为利用上海佘山形变观测资料识别地震异常信息、揭示地壳应力应变的变化过程研究提供更加客观背景特征参考值。此外,在分析具体信号特征时也一定要对台站的地质构造背景、台址条件、周围环境有充分的了解,以便得出正确结论。
- 敬少群,王佳卫,童迎世.2002.小波变换在少震、弱震区地下水位数据分析中的应用[J].华南地震,22(2):9-15.
- 李杰,刘希强,李红,等.2005.利用小波变换方法分析形变观测资料的正常背景变化特征[J].地震学报,27(1):33-41.
- 宋治平,武安绪,王梅,等.2003.小波分析方法在形变数字化资料处理中的应用[J].大地测量与地球动力学,23(4):21-27.
- 万永革.2007.数字信号处理的MATLAB实现[M].北京:科学出版社.
- 武安绪,鲁亚军,李平安,等.2007.基于二进小波的数字形变资料趋势异常分析探讨[J].东北地震研究,23(2):16-21.
- 张贤达,保铮,1995.非平稳信号分析与处理[M].北京:国防工业出版社.
- 张燕,吴云,刘永启,等.2004.小波分析在地壳形变资料处理中的应用[J].地震学报,26(增刊):103-109.
- 张永志,王双绪.1998.河西地区地壳垂直形变的小波分析结果与中强震关系研究[J].地震学报,20(2):150-157.
- 张永志,王文萍,牛安福.1999.华北定点形变的小波分析与地震活动研究[J].地壳形变与地震,18(3):48-54.