基金项目:地震科技星火计划项目(XH12051Y),青海省地震科学基金(2010A04)联合资助.
(1.青海省地震局,青海 西宁 810001; 2.中国地震局地球物理研究所,北京 100081)
(1.Earthquake Administration of Qinghai Province,Xining 810000,Qinghai,China)(2.Institute of Geophysics,CEA,Beijing 100081,China)
earth free oscillations; gravity observation data; Japan M9.0 Earthquake; Golmud Reference Seismological Station
备注
基金项目:地震科技星火计划项目(XH12051Y),青海省地震科学基金(2010A04)联合资助.
利用格尔木基准地震台重力观测资料,检测到2011年3月11日日本东海岸9.0级特大地震激发 0S0~0S40之间的球型自由振荡,其中有 0S0、 0S13、 0S22、 0S26、 0S30共5个振型的
By use of the gravity digital observation data recorded at Golmud Reference Seismological Station,we detect the spherical free oscillation between the mode of 0S0 and 0S40 stimulated by the M9.0 earthquake occurred on March 11,2011 in Japan.The difference between the theoretical and the observed frequency values of the mode of 0S0、 0S13、 0S22、 0S26、 0S30 is almost zero.Meanwhile,we find that the mode of 0S2 and 0S3 have the phenomenon of spectra line splitting.But it is difficult to identify the mode of 0S32 and 0S37,because they are drowned in the noises.The whole mean deviation is about 0.10%,which shows that there is a good agreement between observed and theoretical frequency values.The results not only suggest the validity of the theory of Preliminary Reference Earth Model,but also show the excellent of gravity data recorded at Golmud Reference Seismological Station,so it maybe helpful to understand the structure in deep earth.
引言
特大地震发生后,通常会产生延续几天甚至几个星期的全球自由振荡,只有长周期重力仪、地震仪等才能记录到这种振荡。最早对地球自由振荡作出准确观测是1960年5月22日智利8.9级地震后,Benioff等(1961)与Ness等(1961)分别用Isabella应变仪和Lacoste-Romberg重力仪实现的,两个观测结果非常吻合并与理论值一致,使人们知道了长周期自由振荡的存在。目前人们认识到的自由振荡有两种:第一种是球型振荡,地球作球型振荡时,其质点位移既有径向分量,也有水平分量; 第二种是环型振荡,地球作环型振荡时,各质点只在以地心为球心的同心球面上振动,位移无径向分量,地球介质只产生剪切形变,无体积变化,地球的重力场不受扰动,因此重力仪记录不到这种振荡。
近年来全球大地震频繁发生:2001年昆仑山口8.1级地震、2004年印尼苏门答腊9.0级地震、2008年汶川8.0级地震、2011年日本9.0级地震等,这些罕见的大地震为人们研究地球自由振荡提供了良好的机会。不少研究者利用数字观测资料研究了一些大地震激发的地球自由振荡,如万永革等(2004,2005,2007)利用中国数字地台网的资料研究了2001年昆仑山口西8.1级地震和2004年印尼苏门答腊大地震激发的地球自由振荡; 雷湘鄂等(2002,2004,2007)利用超导重力仪来观测地球球型自由振荡; 于海英等(2006)、邱泽华等(2007)、唐磊等(2007)、任佳等(2009)、徐晓枫等(2010)、杨跃文等(2010)也分别利用钻孔差应变仪观测资料、中国钻孔应变台网体应变观测资料、水位前兆资料、中国数字地震台网资料、云南水管仪观测资料等研究了苏门答腊地震、汶川地震所激发的地球自由振荡,取得了不少成果,让人们对地球内部结构有了进一步的了解。
格尔木地震台是国家基准台之一,观测手段丰富多样,观测质量在国家数字台网中排名前列。北京时间2011年3月11日13时46分日本东海岸发生了9.0级特大地震,地震后不久,作者立即利用格尔木基准台重力观测数据,检测此次地震激发的 0S0~0S40基频振型自由振荡,并观测到 0S2、 0S3振型谱峰分裂现象,观测效果明显。
1 格尔木重力仪对日本大地震的记录
格尔木地震台位于青藏高原腹地,属于国家基准台,海拔3 118 m。台站观测环境良好,置放仪器的山洞进深28 m,总长30 m,洞顶覆盖大于40 m,侧向覆盖大于30 m,洞内岩石为花岗岩,岩石比较坚硬完整,主体山脉基本无植被,且方圆3 km内没有大的活动断裂通过。台站使用PET型固体潮重力仪,该仪器漂移率小、精度高、测量范围宽,2008年开始投入使用,目前运行稳定,产出数据质量良好,观测数值单位为μGal(1 μGal=10-8 m·s-2)。
2011年3月11日日本东海岸附近(38.1°N,142.6°E)发生9.0级特大地震,格尔木基准地震台重力仪清晰地记录到这次大地震。图1为格尔木基准台重力仪记录的日本9.0级特大地震的分钟值曲线,图中信号清晰,可清楚地看到重力潮汐和地震波。
2 数据选取及计算方法
我们选取数据长度为2011年3月11日13时00分至3月18日12时59分,共168小时,功率谱中频率分辨率为1.67×10-6 Hz,适当的频率分辨率是辨认振型谱峰的前提。通常用功率谱来描述随机信号的频域特征,这是一个统计平均的频谱特征。功率谱的目的是根据有限数据给出信号及随机过程的频率成分布的描述,提取淹没在噪声中的有用信息。采用改进的平均周期图法来求取随机信号的功率谱密度估计,并运用信号重叠分段、加窗函数与FFT算法等提高运算效率与效果。设信号x的自相关函数为Rn,则定义其Fourier变换为该信号的功率谱密度估计(万永革,2007),即
Sk=∑N-1n=0Rne-i(2πnk)/N,k=0,1,2,…,N-1.(1)
式中,自相关函数
Rn=1/N∑N-1j=0xjxj+n,n=-(N-2),
-(N-1),…,N-2,N-1. /((2))
式中,N为计算所用数据的数目,由于我们计算重力资料地球自由振荡信息时采用的记录是分钟值,故N取10 080,x为重力数据,Sk离散值为功率谱密度值。另外,为了消除数据不能无限长而必须加窗对功率谱密度估计造成的影响,根据窗函数的不同特性,笔者采用Hanning窗来抑制功率谱旁瓣,突出主瓣,以获取较准确的频谱信息。为了时间截取上的便利,计算的数据包含了地震波传到仪器之前的54个数据,但其相对于整个数据长度是微不足道的,不会影响分析结果。
笔者参考雷湘鄂等(2007)的甄别方法,即每个检测振型的谱峰值与该振型附近的观测背景噪声谱的比值,即该振型的信噪比,若被检测振型的信噪比大于3就是有效检测。
为了观察是否存在着能贡献出类似于自由振荡信息的非地震因素,我们对地震之前的重力资料进行分析,从而确定检测到的自由振荡信息为日本地震所激发的。
3 计算结果
3.1 震后功率谱密度估计谱采用上述的数据与方法,我们得到的格尔木地震台重力观测数据日本大地震后的功率谱密度估计谱,如图2所示,观测频段依次分别为0.28~1.80,1.80~2.90,2.90~3.85和3.85~4.75 mHz。计算结果清晰地检测到了 0S0~0S40之间除 0S32、 0S37振型之外基频振型自由振荡系列。为了对观测到的自由振荡和PREM模型的理论自由振荡周期进行对比,图中用虚线指示PREM模型的理论自由振荡频率值。
图2a所示为在0.28~1.80 mHz频段内检测到的基型振荡 0S0~0S10。由图可以看出,整个频段无较大干扰,各个振型附近噪音很小,信噪比均大于3,能将 0S0~0S10振型有效检测出来。虽然 0S2和 0S3振型相对于其它振型观测效果不明显,但是由于其周围噪声很微弱,依然能将其检测出来。由目前的工作可知(万永革等,2007; 雷湘鄂等,2007), 0S2和 0S3振型存在着谱线分解的情况。一般情况下,观测人员观测到 0S2和0S3并不像其它振型那么明显,这可能有两个原因:一是因为 0S2和 0S3振型是低频率的低阶振型,一般地
震难以激发,只有大地震发生时才能被观察到; 另一方面可能是由于其能量的分散,谱线的分裂意味着能量的分散, 0S2和 0S3振型的能量分散于理论频率值附近的几个谱峰,不易观察。图2 不同频段重力记录功率谱密度估计曲线
(a)0.28~1.80 mHz;(b)1.80~2.90 mHz;
(c)2.90~3.85 mHz;(d)3.85~4.75 mHz
Fig.2 Estimation curve of power spectrum density of the gravity records in different frequency range (a)0.28~1.80 mHz,(b)1.80~2.90 mHz,(c)2.90~3.85 mHz,(d)3.85~4.75 mHz图2b所示为在1.80~2.90 mHz频段内检测到的 0S11~0S20振型,该频段噪声较低,信噪比较高,观测的振型附近无较大干扰,观测效果清晰,且观测频率值与理论值相差甚微。
图2c所示为在2.90~3.85 mHz频段内检测到的 0S21~0S30振型,据图可知,除0S28振型观测频率值与理论数值偏差稍微大外,其余振型检测效果良好。
图2d所示为在3.85~4.75 mHz频段内检测到的 0S31~0S40振型,该频段的噪声较大,其中 0S32和 0S37振型未形成突出的谱峰,导致观测效果不明显,尽管如此,依然较清晰地检测到了这些振型,不过观测频率值与理论值偏差相对于其他频段较大。
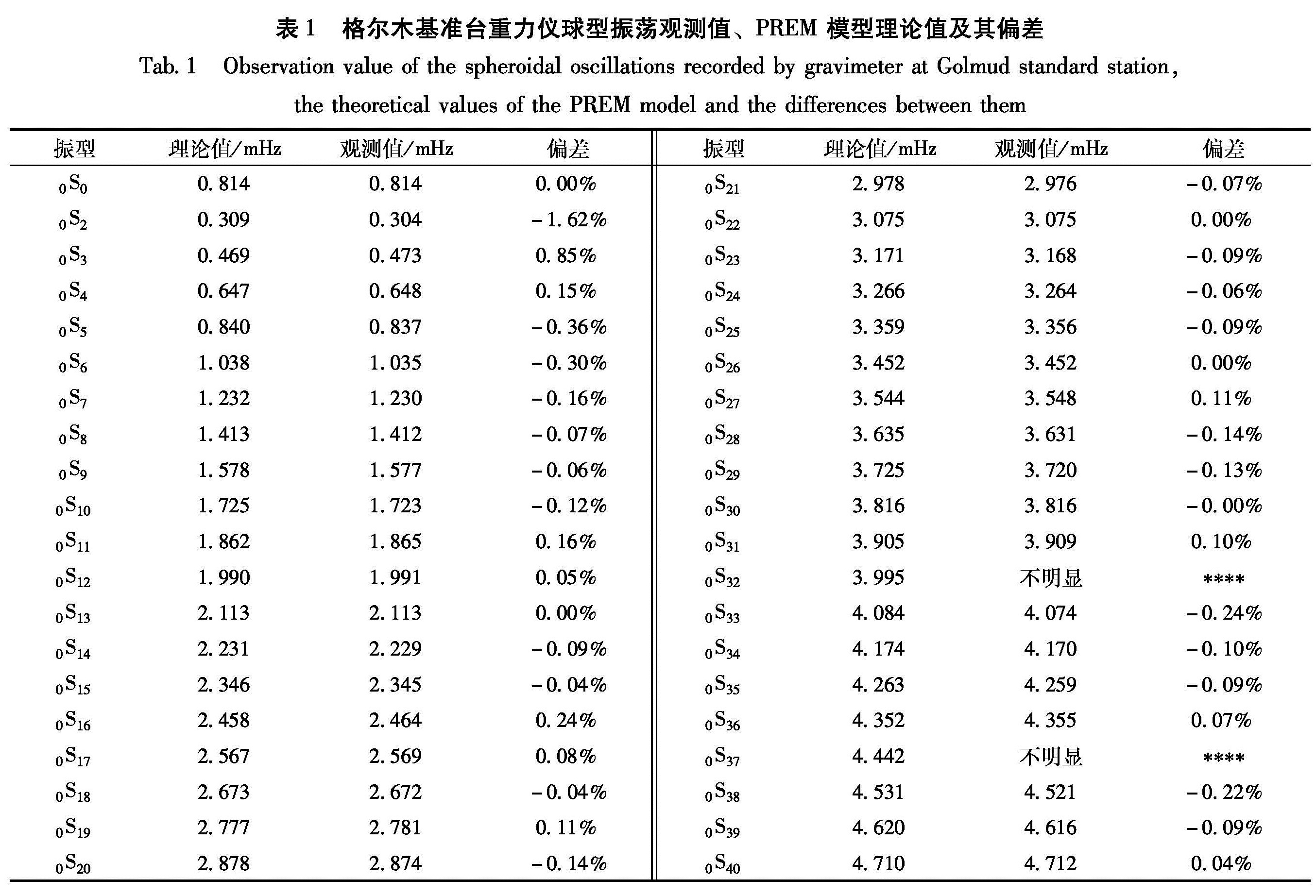
将球型振荡 0S0~0S40振型观测频率值与PREM模型理论值进行比较(表1)可见, 0S2、 0S3振型观测频率值与理论值偏差较大,分别为-1.62%与0.85%,这并不是观测的失误,而可能是 0S2、 0S3振型谱线分裂所致; 而频率较高的 0S32、 0S37振型由于未能与周围的噪音区分出来,没有很好的观测效果。同时,可以看出 0S0、 0S13、 0S22、 0S26和 0S30共5个振型的观测频率与理论值偏差近似为0,这是很少观测到的现象。除去 0S2、 0S3、 0S32、 0S37振型,偏差绝对值大于0.20%以上的仅有5个振型: 0S5、 0S6、 0S16、 0S33和 0S38; 而小于0.10%的振型有20个,总体平均偏差为0.10%。在计算总体平均偏差的过程中, 0S2、 0S3振型存在谱线分裂, 0S32、 0S37振型未能分辨出,故这4个振型不在计算之列。
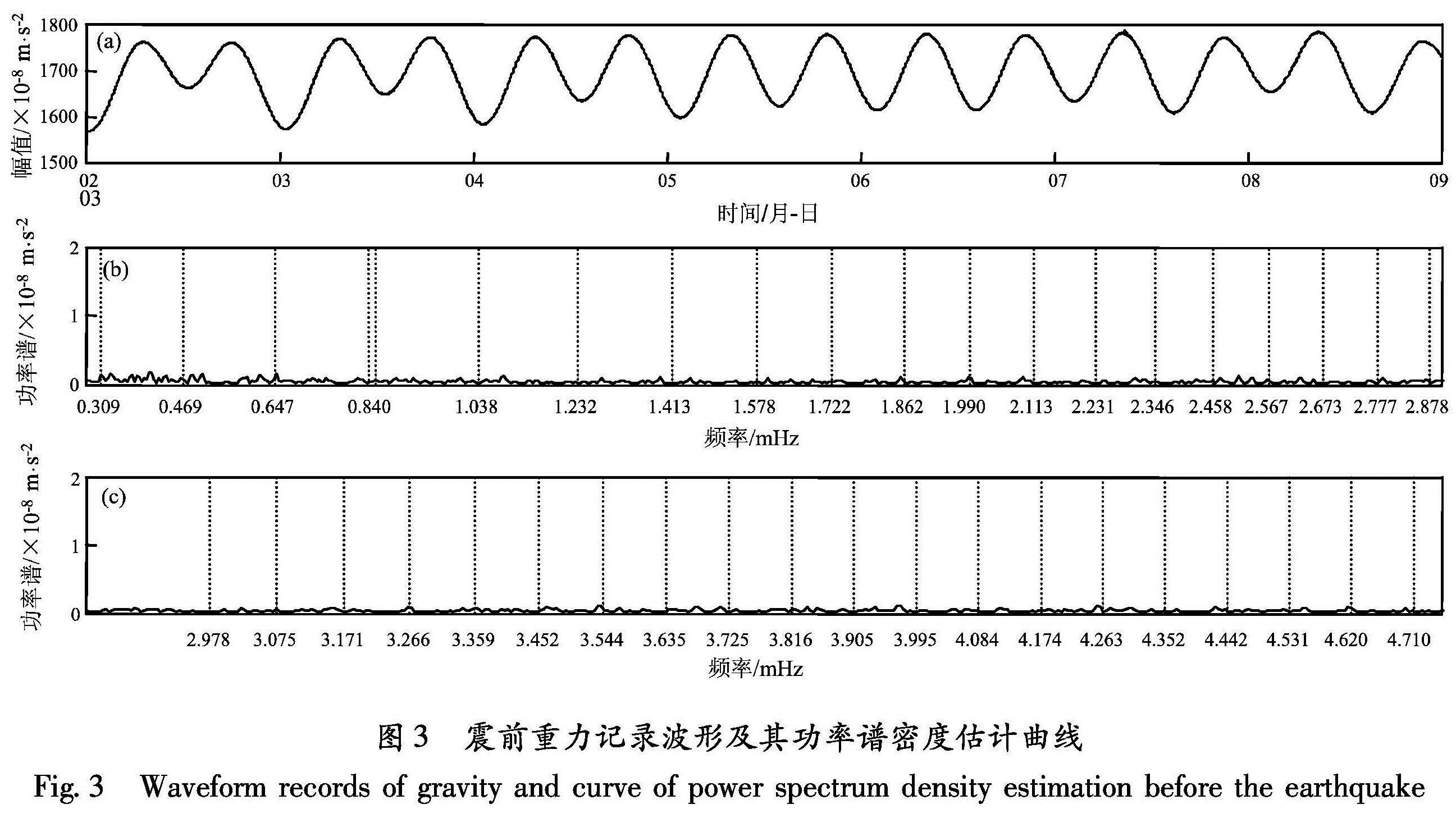
3.2 震前重力数据功率谱检测为了检验其他因素是否对此次检测到的自由振荡信息有影响,我们对地震之前的重力资料进行分析,观察是否有类似于自由振荡信息存在。截取2011年3月2日0时0分至3月8日23时59分的重力数据,数据长度与前面一致,按照前文介绍的方法进行计算,这样将3月9日日本7.2级地震可能产生的影响排除掉。从这段数据的功率谱上可以看出,在检测的频率范围内,并无太大的背景干扰,噪音很小,潮汐因素也并未对所研究的频段造成太大的影响,因此,我们可以确定检测到的信号大部分来自日本9.0级大地震引起的自由振荡信息(图3)。
3.3 0S2、 0S3振型的谱线分裂
由于地球自转与扁率的影响,地球的某些
本征振荡不是简并的,而是存在谱线分裂现象。地球自由振荡的简正振型表现为一些离散的频谱峰,频谱峰的位置可以用来确定球面上的平均地幔结构,而频谱峰分裂是大尺度的非球状和非均匀地球的证据(Widmer-Schnidrig,1999)。Dahlen
表1 格尔木基准台重力仪球型振荡观测值、PREM 模型理论值及其偏差
Tab.1 Observation value of the spheroidal oscillations recorded by gravimeter at Golmud standard station,the theoretical values of the PREM model and the differences between them图3 震前重力记录波形及其功率谱密度估计曲线
Fig.3 Waveform records of gravity and curve of power spectrum density estimation before the earthquake等(1968,1969)利用扰动理论分析了地球自转及扁率作用导致的地球自由振荡谱分裂,并把相关分裂参数制成表格形式,从理论上详细地分析了科里奥利力分裂效应。现在人们对地球自转和扁率引起自由振荡谱线分裂的研究已比较成熟,可以将实测振型的谱线分裂与模型理论预测值进行比较。
谱线分裂的振型一般都包括两个或两个以上的分裂谱峰,频率最高的谱峰与频率最低的谱峰之间频率差为实测谱线分裂宽度W,振型谱线分裂宽度的理论值Wth,定义用谱线分裂率R为实测谱线分裂宽度W与理论谱线分裂宽度Wth之比值(雷湘鄂等,2007),即
R=W/Wth.(3)
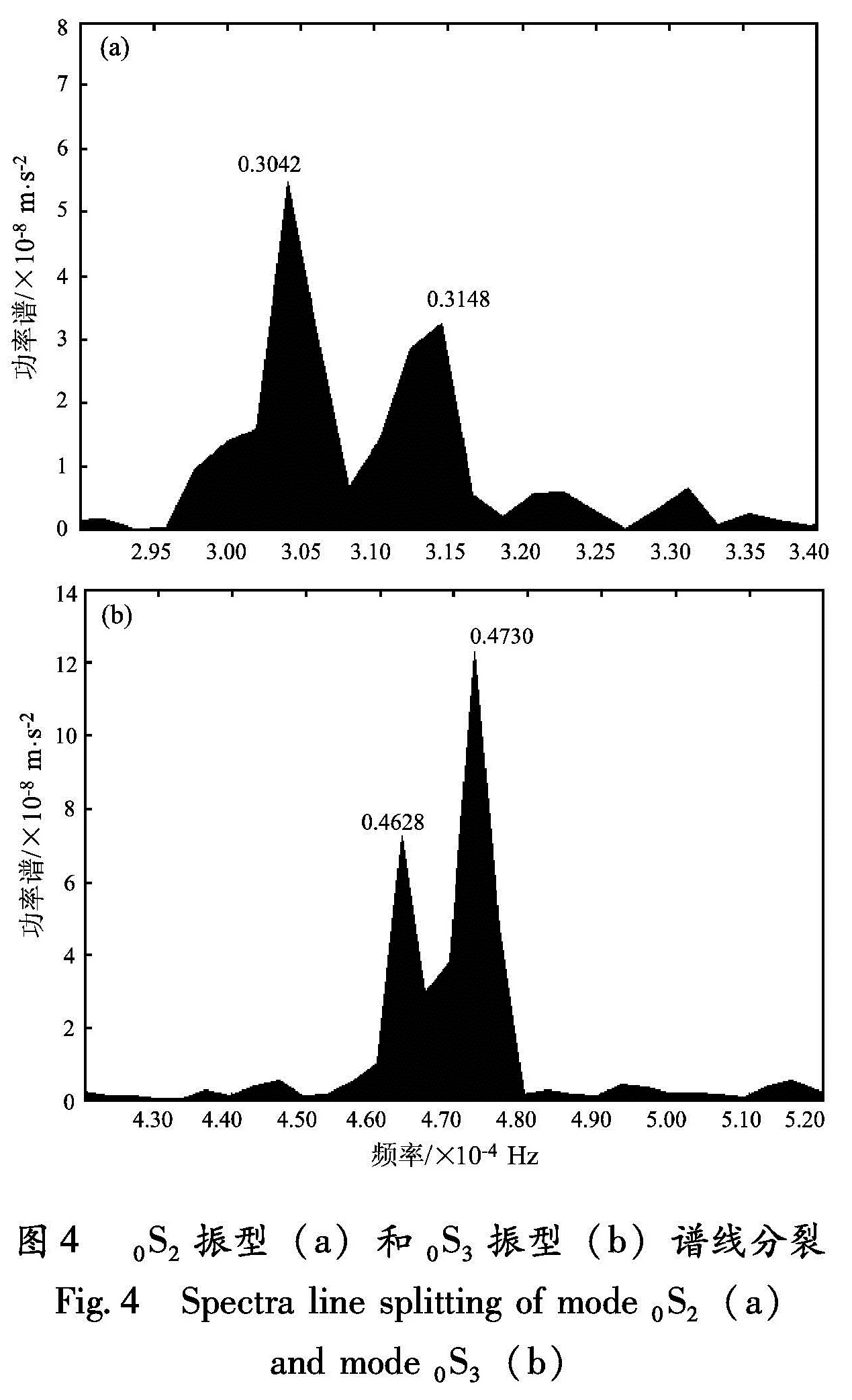
从图4中可以看出, 0S2、 0S3振型各有两个谱峰,每个谱峰的信噪比都大于3,故能将其分辨出。实测谱线分裂宽度、理论宽度分别为W1=10.60×10-6 Hz,W2=10.20×10-6 Hz,Wth1=
19.48×10-6 Hz,Wth2=13.05×10-6 Hz。谱线分裂率分别为R1=0.544,R2=0.782。这个结果要小于雷湘鄂等(2007)用武汉超导重力仪研究苏门答腊地震时得到数值(其结果分别为1.07,1.13)。方明(1991)指出,利用由地表向地心的数值积分计算自由振荡 0Sn的周期时,发现只有 0S2和 0S3振型的穿透深度进入内核,其中 0S2的穿透深度接近地心,而 0S3的穿透深度则刚刚进入内核。可见某些特殊振型的分裂能反映地球内核结构的复杂性,本文结果与雷湘鄂等(2007)的结果不同,可能是地球内核各向异性的表现。 0S2、 0S3振型存在着谱线分裂的现象,能量被分解,也正说明了 0S2、 0S3振型难以明显观测的原因。图4 0S2振型(a)和 0S3振型(b)谱线分裂
Fig.4 Spectra line splitting of mode 0S2(a) and mode 0S3(b)4 结论与讨论
(1)运用格尔木地震台PET型固体潮重力仪记录的资料,除 0S32、 0S37振型之外,准确检测到了日本9.0级地震激发的 0S0~0S40振型球型自由振荡,与PREM理论自由振荡频率进行对比,发现实测的频率值与PREM理论值有很好相符,两者互相吻合,既证明了PREM理论的正确性,也反映了台站重力记录质量良好。
(2)计算过程中未对观测数据进行扣除固体潮的数字处理,但经过对震前重力资料的处理,并没发现相似的地球自由振荡信息,整个研究的频率范围噪音很微弱,可见这样的处理是合适的。
(3)经过反复观察,并参照前人研究成果,认为0S2、 0S3振型难以观测的原因一方面在于其难以激发,需能量较大的地震才能将其激发出来,另一面更在于0S2、 0S3振型存在着谱线分裂的现象,能量被分散在邻近的几个频率,故在功率谱上较难观测。
(4)本文利用格尔木基准地震台重力记录检测到的日本大地震激发的地球自由振荡资料还可能包含其他振动源的贡献,特别是地震后原震区附近大规模的海啸对观测到的地球自由振荡的影响,还需进一步研究。
感谢格尔木基准地震台李启雷、李玉丽提供的帮助。
- 方明.1991.地球自由振荡——正演、反演理论中若干问题的研究[D].北京:中国科学院测量与地球物理研究所.
- 雷湘鄂,孙和平,许厚泽,等.2007.苏门达腊大地震激发的地球自由振荡及其谱线分裂的检测与讨论[J].中国科学D辑:地球科学,37(4):504-511.
- 雷湘鄂,许厚泽,孙和平.2002.利用超导重力观测资料检测地球自由振荡[J].科学通报,47(18):1 432-1 436.
- 雷湘鄂,许厚泽,孙和平.2004.由5个国际超导重力仪台站资料检测到的秘鲁8.2级大地震所激发的球型自由振荡现象[J].中国科学D辑:地球科学,34(5):483-491.
- 邱泽华,马瑾,池顺良,等.2007.钻孔差应变仪观测的苏门答腊大地震激发的地球环型自由振荡[J].地球物理学报,50(3):797-805.
- 任佳,陈华静,蒋翠荣,等.2009.数字化水位仪观测的苏门答腊大地震激发的地球球型自由振荡[J].地震研究,32(4):333-338.
- 唐磊,邱泽华,阚宝祥.2007.中国钻孔体应变台网观测到的地球球型振荡[J].大地测量与地球动力学,27(6):37-44.
- 万永革,盛书中,周公威,等.2007.中国数字地震台网记录的苏门答腊—安达曼地震激发的地球球型自由振荡的检测[J].地震学报,29(4):369-381.
- 万永革,周公威,郭燕平,等.2004.昆仑山口西地震激发的地球环型振荡[J].防灾减灾工程学报,24(1):1-7.
- 万永革,周公威,郭燕平.2005.中国数字地震台网记录的昆仑山口西地震的球型自由振荡[J].地震,25(1):31-40.
- 万永革.2007.数字信号处理的MATLAB实现[M].北京:地震出版社.
- 徐晓枫,万永革,王惠琳.2010.由中国CDSN台网检测到的汶川地震所激发的地球球型自由振荡[J].地震,30(1):36-49.
- 杨跃文,秦嘉政,任佳,等.2010.利用云南水管仪观测资料检测地球自由振荡[J].地震研究,33(2):189-194.
- 于海英,朱元清,寿海涛.2006.印度洋9.0级大地震激发的地球球型振荡和环型振荡[J].地球物理学进展,21(3):706-716.
- Benioff H,Press F,Smith S.1961.Excitation of the free oscillations of the earth by earthquake[J].J Geophys Res,66(2):605-619.
- Dahlen F A.1968.The normal modes of a rotating,elliptical earth[J].Geophys J Rastr,16(4):329-367.
- Dahlen F A.1969.The normal modes of a rotating,elliptical earth——11 near-resonance multiplet coupling[J].Geophys J Rastr,18(4):397-436.
- Ness N R,Harrison C T,Slichter L B.1961.Observation of the free oscillation of the earth[J].J Geophys Res,66(2):621-629.
- Widmer-Schnidrig R.1999.Free oscillations illuminate the mantle[J].Nature,398:292-293.