极值理论是概率论中的一个重要分支,也是统计预报地震的重要方法之一。 Nordquist(1945)最早将Gumbel极值分布应用于地震统计,其后,国内外许多学者应用和发展了Gumbel理论,使其在地震预报、地震危险性分析、工程地震安全性评价及地震区划等诸多地震领域都有着重要应用(Epstein,Lomnitz,1966; Yegulalp,Kuo,1974; Huillet,Raynaud,1999; 高孟潭,贾素娟,1988; 贾素娟,鄢家全,1996)。考虑到震级应有上限,陈培善和林邦慧(1973)给出了极值分布的修正式,并对我国14个地震带作了内符检验和预测。陈虹等(1995,1996)通过将极值分布线性组合成混合极值分布研究了大陆和东南沿海各震区的地震危险性,一定程度上弥补了在震级较大区间内I型极值相对观测值偏高,而III型相对观测值偏低的缺点。由于地震活动的复杂性,各地区地震震级分布存在很大的差异,在我国各多震区,各种极值类型分布有着不同的适用性(秦卫平,1983; 张卫东等,2005)。因此在实际应用过程中,对模型的选择就显得非常重要,如果模型分布选择不当,可能会带来严重偏差。广义极值分布可以统一3种类型极值渐近分布(De Haan,Ferreira,2006),本文基于广义极值分布讨论地震危险性分析,给出了几种与地震预报有关的公式和预报方法,并以台湾地区震级资料为基础,分析了未来不同年份地震危险性。

设X₁,X₂,…,X_n是独立同分布的随机变量列,有共同的分布函数F(x),记为M_n=max(X₁,X₂,…,X_n),若存在{a_n>0,b_n∈R}和非退化分布函数G(x),使

(M_n-b_n)/(a_n)〖FY(〗b〖FY)〗 G(n→∞).(1)

则称G为极值分布,并称F为属于G的吸引场,记作F∈D(G)。Fisher和Tippett(1928)证明了极值分布的3大类型定理,指出G必属于下列3种类型之一:

Ⅰ.Gumbel Λ(x)=e^-e-(x-μ)/σ,x∈R,σ>0;

Ⅱ.FrechetΦ_α(x)={ 0, x≤μ,

e^{-((x-μ)/σ)-α},x>μ,σ>0,α<0;

Ⅲ.WeibullΨ_α(x)={e^{-((x-μ)/σ)-α},x>μ,

1, x>μ,σ<0,α<0.(2)

其中, μ为位置参数,σ为尺度参数,α为极值指标。

如果知道地震震级分布的类型,并且能验证其是否满足极值分布吸引场条件(史道济,2006),就可以确定相关问题的极值分布属于什么类型,但是通常只能获得观测数据,而其具有何种分布是难以确定的。另外,即使知道分布类型,也很难验证其是否满足最大值吸引场条件。对于我国各个多震地区,以往应用极值理论来分析地震危险性时往往单独采用3种分布中的一种,而忽视满足其分布的条件。

广义极值分布包含了以上3种分布,是极值分布的统一形式,其分布函数为

G_ξ(x)=exp{-(1+ξ(x-μ)/σ)^-1/ξ},(3)

其中1+ξ(x-μ)/σ>0,σ>0, ξ∈R, μ∈R。μ为位置参数,σ为尺度参数,ξ为形状参数。当ξ>0时,令ξ=1/α对应极值Ⅱ型分布,位置参数为(μ-ασ),尺度参数为ασ; 当ξ<0时,ξ=-1/α对应极值Ⅲ型分布,位置参数为(μ+ασ),尺度参数为ασ; 当ξ=0时对应极值Ⅰ型分布,因为lim_ξ→0 exp{-(1+ξ(x-μ)/σ)^-1/ξ}=e^-e-(x-μ)/σ.

国内应用极值方法进行地震活动分析时,通常作如下2个假定(陈培善,林邦慧,1973; 夏成明等,2002):

(1)地震震级x和相应的发震频度n(x)遵守古登堡-里克特(G-R)经验公式:

lnn(x)=a-bx.(4)

(2)单位时间内发生大于某个震级的地震次数η服从泊松分布:

P(η=k)=(λ^k)/(k!)e^-λ,(λ>0,k=0,1,2,…).(5)

在这2个假定下可以推导出地震震级分布为指数分布:

F(x)=1-e^-βx,x>0,β=bln10,(6)

单位时间内最大地震震级分布为

G(x)=e^-e-β(x-μ), μ=lnλ/β.(7)

这实际上与极值统计中得到的指数分布属于Gumbel分布吸引场的结果是一致的。而事实上除指数分布外还有很多分布也属于Gumbel分布吸引场。最大值的渐进分布若存在,则也属于广义极值分布,这从另一个侧面说明在应用极值理论作统计分析时,直接从广义极值分布模型出发将具有更广的适用性。

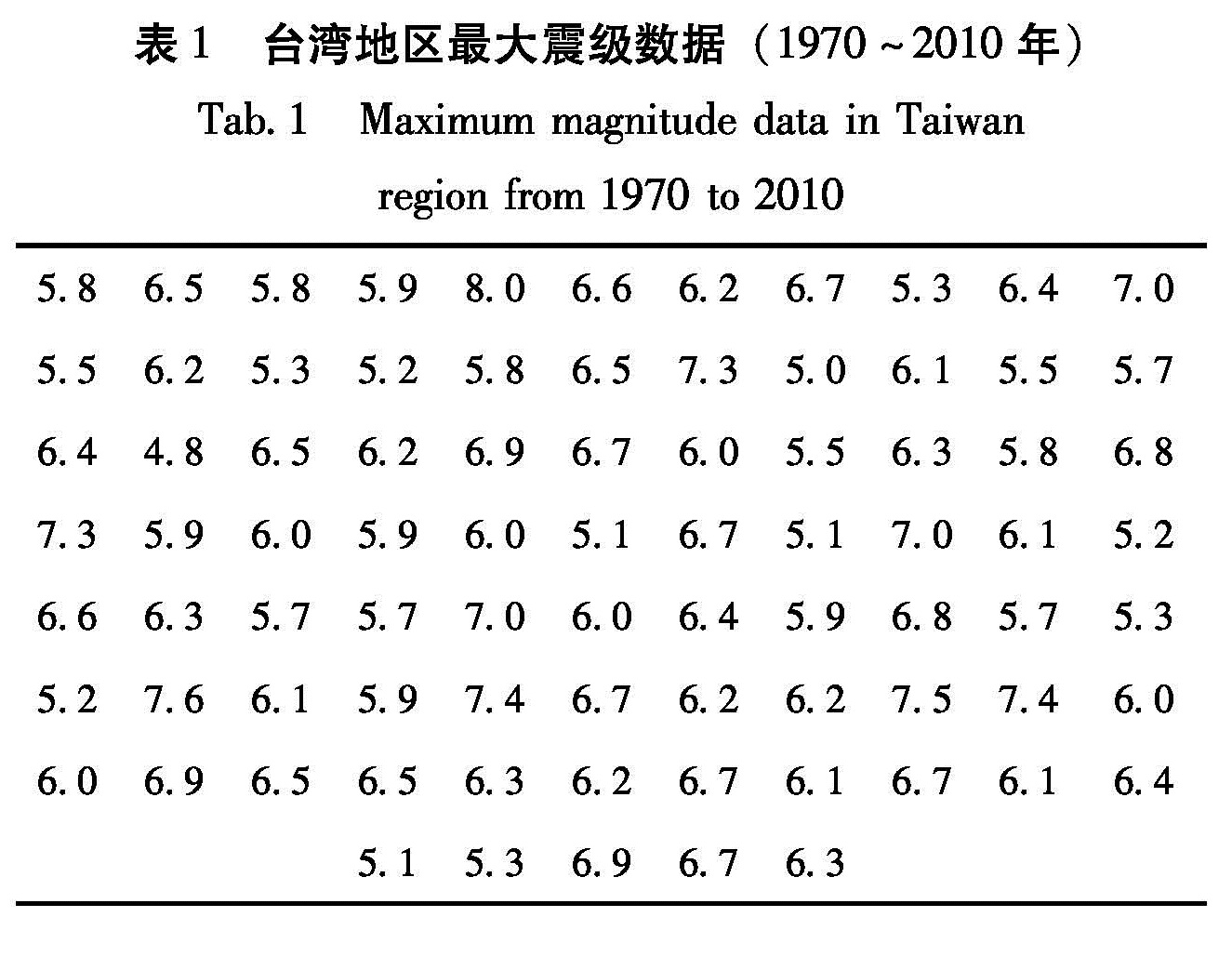
广义极值分布为观测值的最大值提供了一个理想的模型,应用时一般是按等长度对数据进行分组,并以广义极值分布作为区组最大值序列的模型。本文采用中国地震信息网 http://www.csi.ac.cn.提供的地震目录,选取1970年1月1日至2010年12月31日台湾地区(22°～26°N,120°～125.5°E)共41年的M_S≥2.7地震为基础数据,以6个月为时间步长进行区组最大值统计,得到研究区间内每半年地震最大震级数据(表1)。

表1 台湾地区最大震级数据(1970～2010年)
Tab.1 Maximum magnitude data in Taiwan region from 1970 to 2010

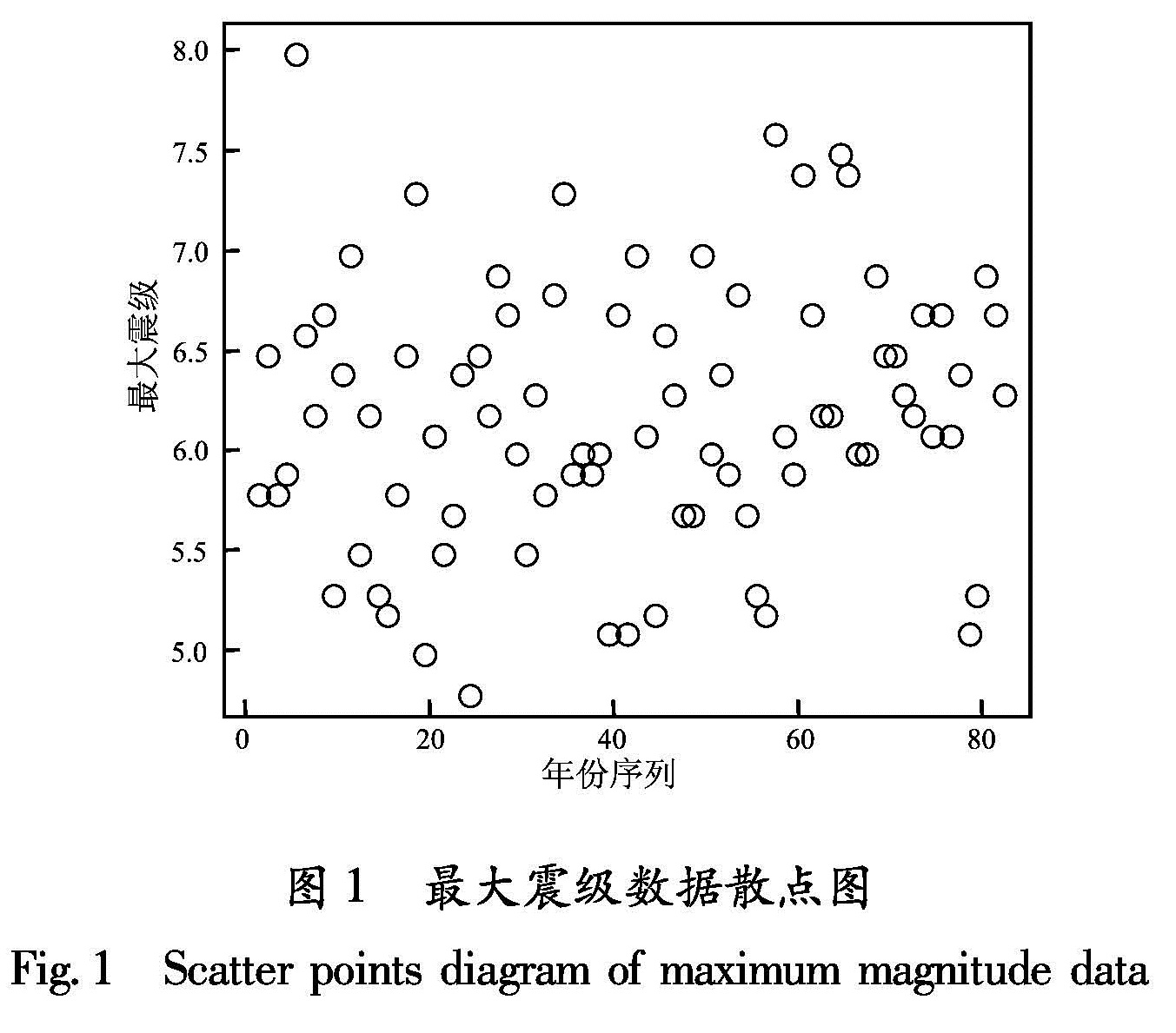
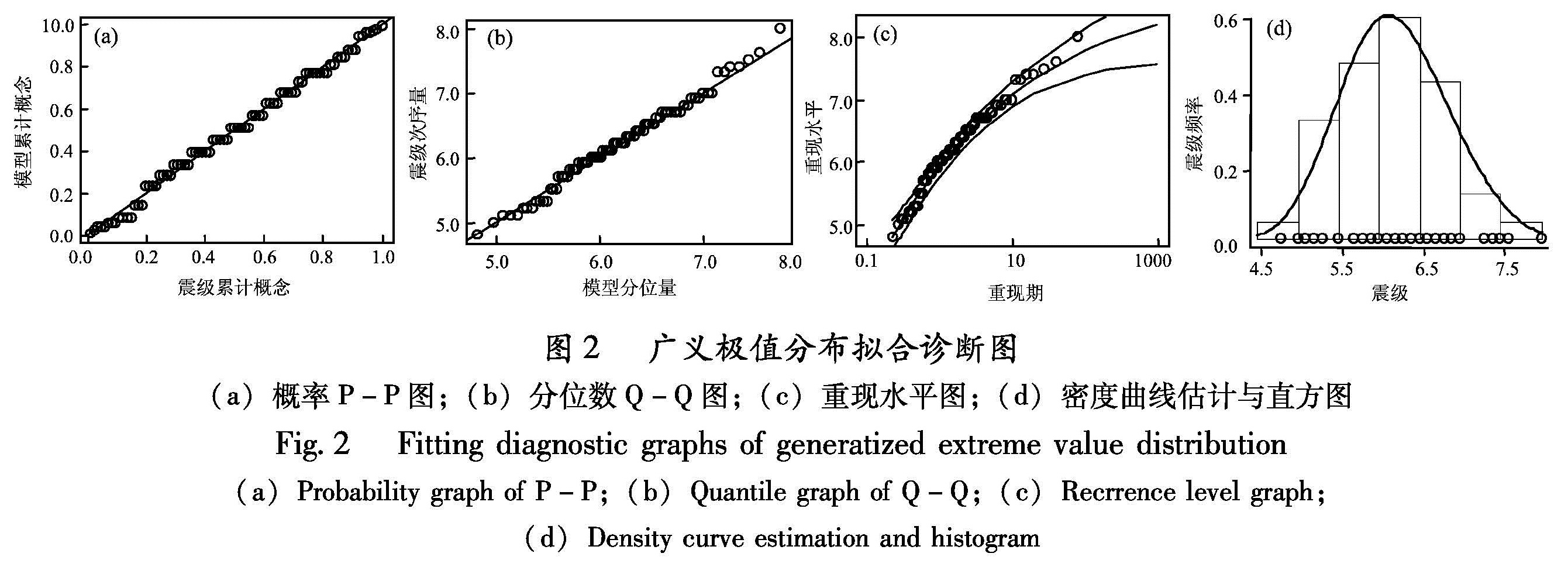
图1是最大震级散点图,图中横轴表示以半年为单位的时间,为简便起见,以序列号代替,纵轴表示每半年最大地震震级M_S。数据显示最大地震震级分布没有明显的变异性,因此可以将观测值看作是来自广义极值分布的样本。实践中极大似然估计是一种比较好的参数估计方法,对复杂模型更具适应性。根据表1的数据使用统计软件R中ismev工具包广义极值.fit命令,可得广义极值分布参数的极大似然估计为(μ^{^},σ^{^},ξ^{^})=(5.953,0.641,-0.224), 估计的标准差分别为0.078、0.055、 0.069。 由估计值和标准差还可知广义极值分布参数μ、σ、ξ的置信度为95%的置信区间分别为[5.80,6.11]、 [0.533,0.749]和[-0.359,-0.089]。ξ的极大似然估计与置信区间都显示为负值,因此台湾地区在研究时间尺度范围内最大震级服从III型极值分布,即对应于一个有界的Weibull分布,符合震级有上界的认识。史道济(2006)介绍了一些常用的模型检验方法,基本的检验方法有P-P图、Q-Q图、直方图等。当数据符合理论假设分布时,P-P图与Q-Q图应近似为直线。直方图是历史悠久且仍广泛使用的方法,可以作为分布密度曲线的近似。另外,估计高分位数(重现水平)是极值分析的主要目的之一,重现水平图可作为模型检验的诊断工具,当ξ=0时为直线,当ξ<0时为凸曲线,当ξ>0时为凹曲线。模型的诊断见图2。

图1 最大震级数据散点图
Fig.1 Scatter points diagram of maximum magnitude data

图2 广义极值分布拟合诊断图
(a)概率P-P图;(b)分位数Q-Q图;(c)重现水平图;(d)密度曲线估计与直方图
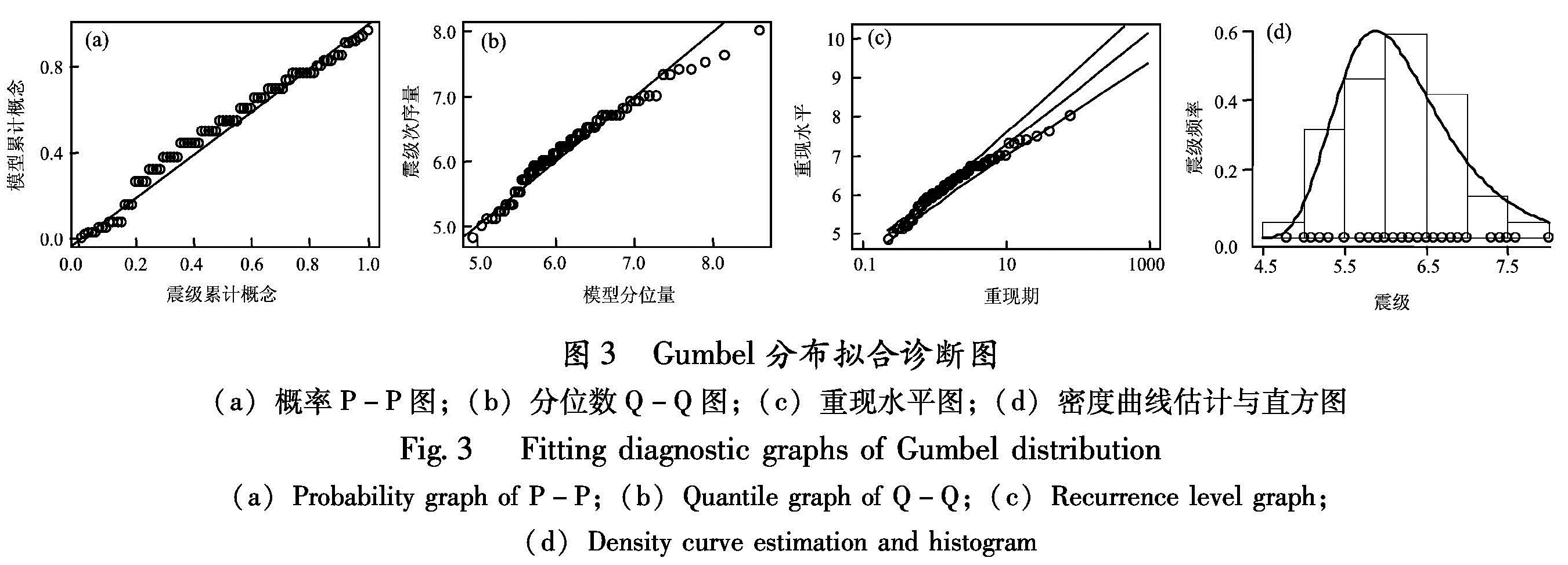
Fig.2 Fitting diagnostic graphs of generatized extreme value distribution(a)Probability graph of P-P;(b)Quantile graph of Q-Q;(c)Recrrence level graph; (d)Density curve estimation and histogram

图3 Gumbel分布拟合诊断图
(a)概率P-P图;(b)分位数Q-Q图;(c)重现水平图;(d)密度曲线估计与直方图
Fig.3 Fitting diagnostic graphs of Gumbel distribution(a)Probability graph of P-P;(b)Quantile graph of Q-Q;(c)Recurrence level graph; (d)Density curve estimation and histogram

从图2a和图2b可看出,所有点都几乎在一条直线上,因此不能否认所拟合的模型。由于ξ的估计值为负,因此相应分布存在有限上界,故重现水平曲线应渐近地趋于某个有限值,且重现水平图为1条凸曲线(图2c)。密度曲线的估计与直方图也显示模型拟合较优(图2d)。因此4个诊断图都支持拟合的广义极值分布模型。图3则是用Gumbel分布模型拟合台湾地区震级数据的模型诊断图,与图2对比可见用该模型拟合效果较差。

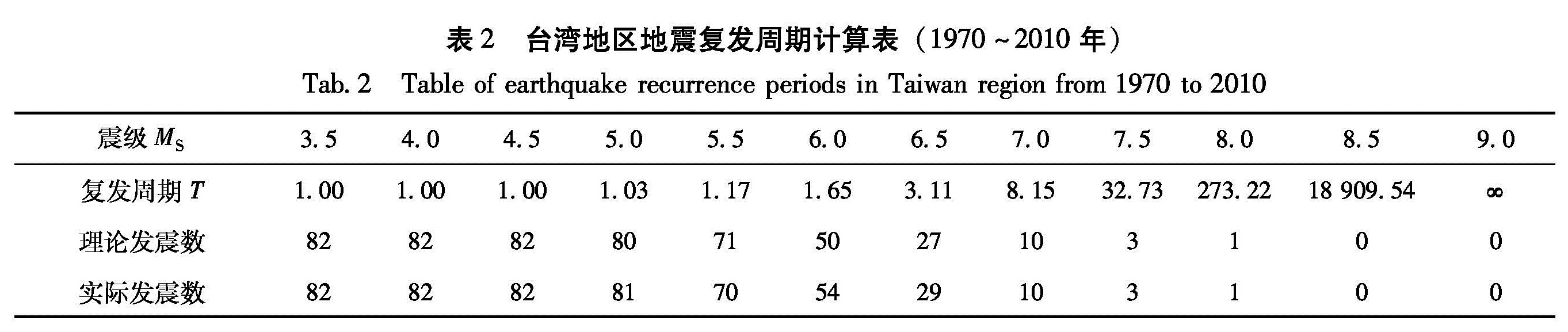
利用第2节中给出的公式,以6个月为时间步长计算1970～2010年台湾地区最大地震震级的平均复发周期及理论发震次数,并预测未来0.5年、1年和5年内发震的概率,计算结果见表2和表3。

表2 台湾地区地震复发周期计算表(1970～2010年)
Tab.2 Table of earthquake recurrence periods in Taiwan region from 1970 to 2010

表3 台湾地区未来T年发震危险性
Tab.3 Seismic risks in the next T years in Taiwan region

(1)针对台湾地区最大震级分布的极值建模,应用Gumbel极值分布拟合效果较差,从分析结果可以看出震级分布服从具有有限上界的Weibull分布。基于广义极值分布的地震危险性分析模型,一方面理论上是合理的,比传统方法更可靠,另一方面也能够避免以往单独采用某一分布的不足。

(2)根据广义极值分布计算出的地震理论发震数与实际发震数相比较,震级超过3.5～4.5级的地震次数理论与实际一致,事实上震级数据中最大震级几乎都超过4.5级。由于极值理论主要特点在分析分布尾部特征,因此比较大的震级发生才是我们所关心的,表2显示M_S≥7.0地震次数符合实际,由此可见极值理论是强震预报中一种较有效的方法之一。震级超过5.0～6.5级的地震次数实际发生数总是大于理论发震数,这可能是因为在所讨论的时间窗口中未能将余震信息删除。余震和震群被认为是非“独立”的事件,是由于较大地震发生后,在其震源区及其附近应力调整而产生的“相关”事件(傅征祥,1997),这在一定程度上削弱了模型应用的变量独立性条件。

(3)从地震发震危险性分析来看,台湾地区半年内发震震级几乎都超过5.0级,发生超过6.0级地震的概率达到0.6; 1年内发生超过6.5级地震的可能性也达到了0.54。从更长时间来看,未来5年台湾地区发生超过6.5级地震的概率为0.98,超过7.0级地震的概率高达0.73,危险性非常高,应引起重视。需要说明的是,以上针对台湾地区41年来的地震基础资料进行的极值分析,仅是从有限的样本中得到的统计特征,随着统计数据样本量的增加,结果可能会更可靠。另外,由于地震活动呈现出地震活跃—平静期交替变化的周期特征和时间空间分布的丛集特点,针对这种呈趋势性的震级序列怎样进行极值统计分析,还值得进一步的研究和探讨。