基金项目:地震行业科研专项“宁洱6.4级地震现场综合考察和研究”(200808061),地震行业科研专项“南北地震带灾区速判与灾情展布关键技术研究”(2008-2012年)与地震行业科研专项“西南地震应急对策新模式与关键技术研究”(20080813)联合资助.
(超高)层建筑环境振动特性实测与统计分析*] 非明伦,周光全,卢永坤,杨树明,代博洋 (云南省地震局,云南 昆明 650224)
(Earthquake Administrator of Yunnan Province,Kunming 650224,Yunnan,China)
high-rise(skyscraper)building; natural vibration period; damping ratio; mathematical regression simulation
备注
基金项目:地震行业科研专项“宁洱6.4级地震现场综合考察和研究”(200808061),地震行业科研专项“南北地震带灾区速判与灾情展布关键技术研究”(2008-2012年)与地震行业科研专项“西南地震应急对策新模式与关键技术研究”(20080813)联合资助.
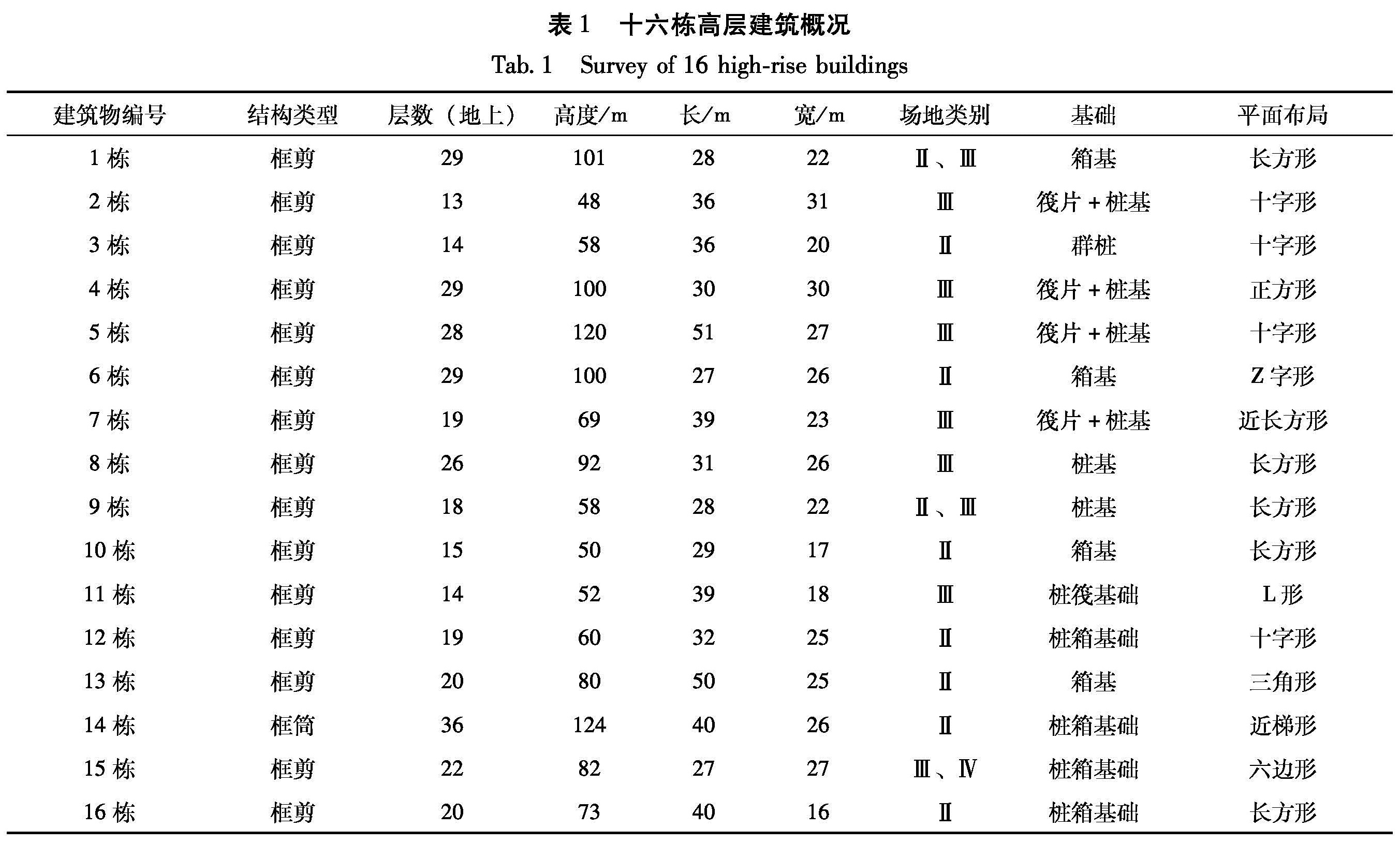
对昆明16栋典型钢筋混凝土高层建筑物的振动特征(包括建筑物的固有频率、振型和阻尼比)进行观测与分析,对地震响应数值模拟研究,获取实测高层建筑物第一至第三振型及结构,计算第一至第二振型自振周期结果,采用数学线性回归方法,模拟得到昆明高(超高)层建筑结构实测第一至三振型和计算第一至第二振型周期公式,为类似建筑结构的设计提供经验和依据。
Having observed and analyzed the vibration characteristics(including inherent frequency,mode and damping ratio)of 16 typical reinforced concrete high-rise buildings in Kunming,and studied the numerical simulation of the seismic response,we obtain Vibration Mode 1-3 and structure of high-rise buildings,and calculate the natural vibration period of Vibration Mode 1-2.Using linear regression methods,we obtain the stimulant formula of the actual measuring of Vibration Mode 1-3 and the theoretical calculating of Vibration Mode 1-2 of high-rise(skyscraper)buildings in Kunming by simulation,which provides experience and basis for the design of similar building structure.
引言
建筑结构在地震作用下的反应与结构物的动力特性密切相关,其自振周期是建筑物的主要动力特性之一,它与许多因素有关,如平面的布置、质量分布、构件刚度、材料特征、施工质量以及地基情况等,可以通过理论计算、实测和试验研究等不同途经来确定建筑物的周期。在20世纪70、80年代,全国各地开展了大量的建筑物自振周期实测工作,获得了大量的实测资料,在实测统计的基础上给出了多层和高层各种结构类型的经验公式。但对于高层或超高层而言,因当时高层建筑数量较少,仅限于北京、广州等地,因此,这些经验公式不能充分反应高层建筑的实际周期。
现今对高(超高)层建筑的抗震设计,需要有较高参考意义的建筑结构物的自振周期。基于这一需求,云南省地震局在“十五”期间对昆明高(超高)层建筑进行中近场强震响应研究,主要研究昆明近场范围内发生强烈地震时,昆明盆地内典型高(超高)层建筑的地震响应。根据设定地震震源模型和对传播路径介质的了解,研究设置震源发生地震破裂时昆明盆地及上覆土层的地震响应,在此基础上研究盆地土—结构相互作用及其对高层建筑的影响。通过理论研究、模型实验、实际观测分析研究昆明市典型高层建筑的地震响应,并提出相应的防震减灾对策,其核心内容是开展昆明盆地地震动场研究及高层建筑结构响应的数值模拟和实验。
本文主要对典型高层建筑的振动特征(指其固有的特性,包括固有频率、振型和阻尼比)进行观测与研究。振动观测的目的是了解建筑物结构的动力特征,为建筑物的安全性评价、损伤识别积累基础资料,为建立合理的建筑数值模型提供依据。 笔者对昆明盆地16栋典型高层建筑进行实测和理论计算结构自振周期和阻尼比,对16栋结构自振周期进行数学回归分析,得到一个适用于昆明高层建筑自振周期的经验公式,并对实测和理论结果进行比较。
1 昆明高(超高)层建筑基本概况
笔者对昆明盆地10层以上453栋高层建筑的建筑结构类型、结构高度、地上(下)层数、建筑物坐落地点、建筑面积、设防烈度、工程造价、室内财产总值、设计单位、竣工年份、建筑用途等情况进行普查。最后从中选取31栋不同结构类型、不同高度、不同座落地点的具有代表性的高层建筑结构,收集它们的建筑设计总说明、结构设计总说明、建筑设计施工图、结构设计施工图及竣工图等详细资料。
昆明盆地高层建筑主要分布在25°00'04″~25°07'19″N,102°38'53″~102°45'00″E范围内,覆盖区总面积82.47 km2 。
2 建筑环境振动测试
3 数学回归分析
3.1 数学模拟模型的建立在已有16栋高层第一至第三振型的实测资料分析基础上,建立数学回归分析数学模型(中国科学院数学研究所统计,1979; 翁文波等,1996; 非明伦等,2007),即假设周期T与楼层δ的线性关系为
T=a + Bδi.(13)
用最小二乘法原理可拟合a,b和相关系数R:
a=1/n∑ni=1Ti-b/n∑ni=1δi,(14)
b=(n∑ni=1(Tiδi)-(∑ni=1δi)(∑ni=1Ti))/(n∑ni=1δ2i-(∑ni=1δi)2),(15)
R=(∑ni=1(Tiδi))/(((∑ni=1T2i)(∑ni=1δ2))1/2).(16)
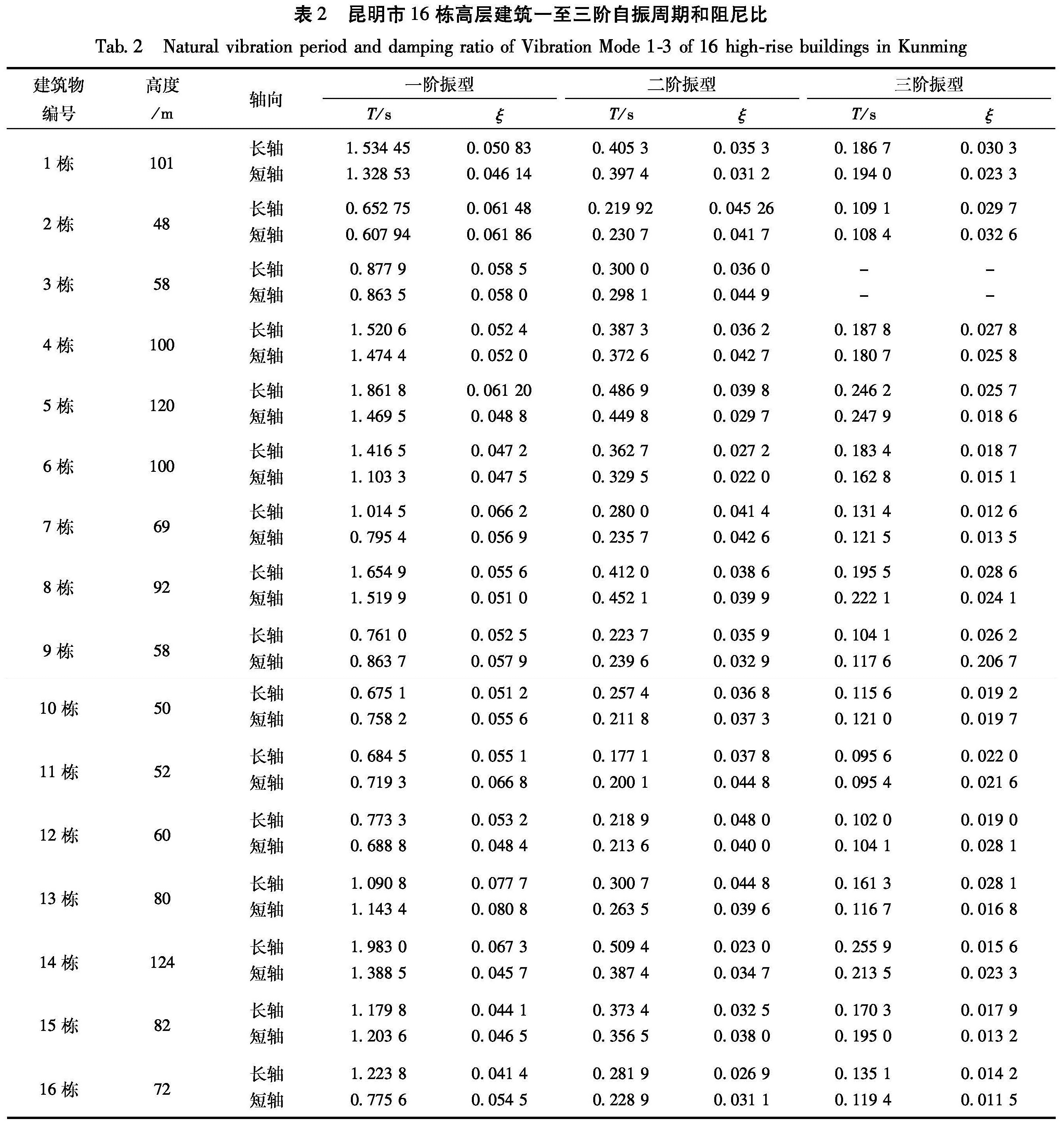
根据表2实测结果模拟得到第一至第三振型的长、短轴方向自振周期关系曲线见图1~3,模拟公式为(17)~(22)。
第一振型
长轴:T1=0.3444e0.0519δ(R2=0.8499),(17)
短轴:T1=0.0398δ+0.148(R2=0.699).(18)
第二振型
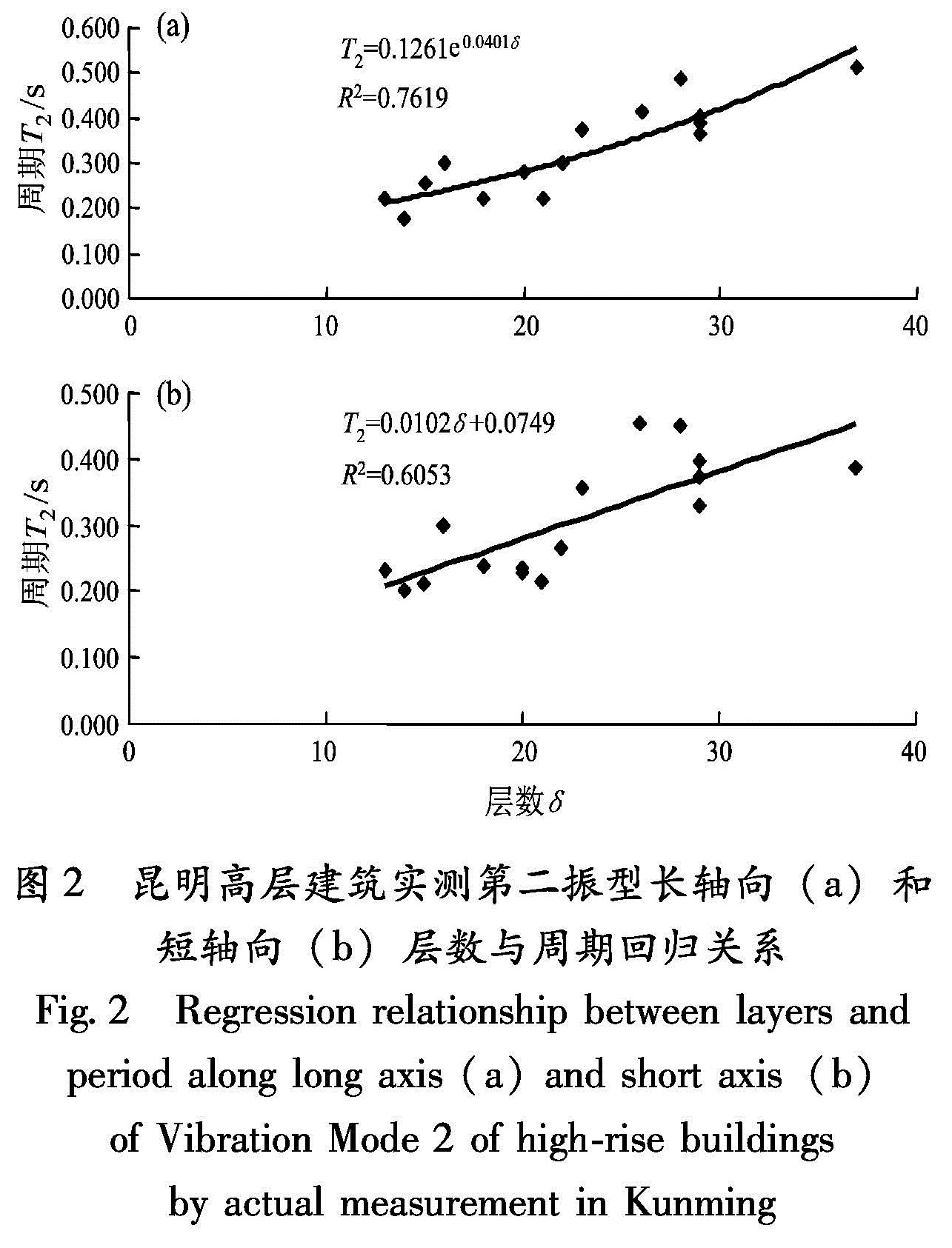
长轴:T2=0.1261e0.0401δ(R2=0.7619),(19)
短轴:T2=0.0102δ+0.0749(R2=0.6053).(20)图1 昆明高层建筑实测第一振型长轴向(a)和短轴向(b)层数与周期的回归关系
Fig.1 Regression relationship between layers and period along long axis(a)and short axis(b)of Vibration Mode 1 of high-rise buildings by actual measurement in Kunming第三振型
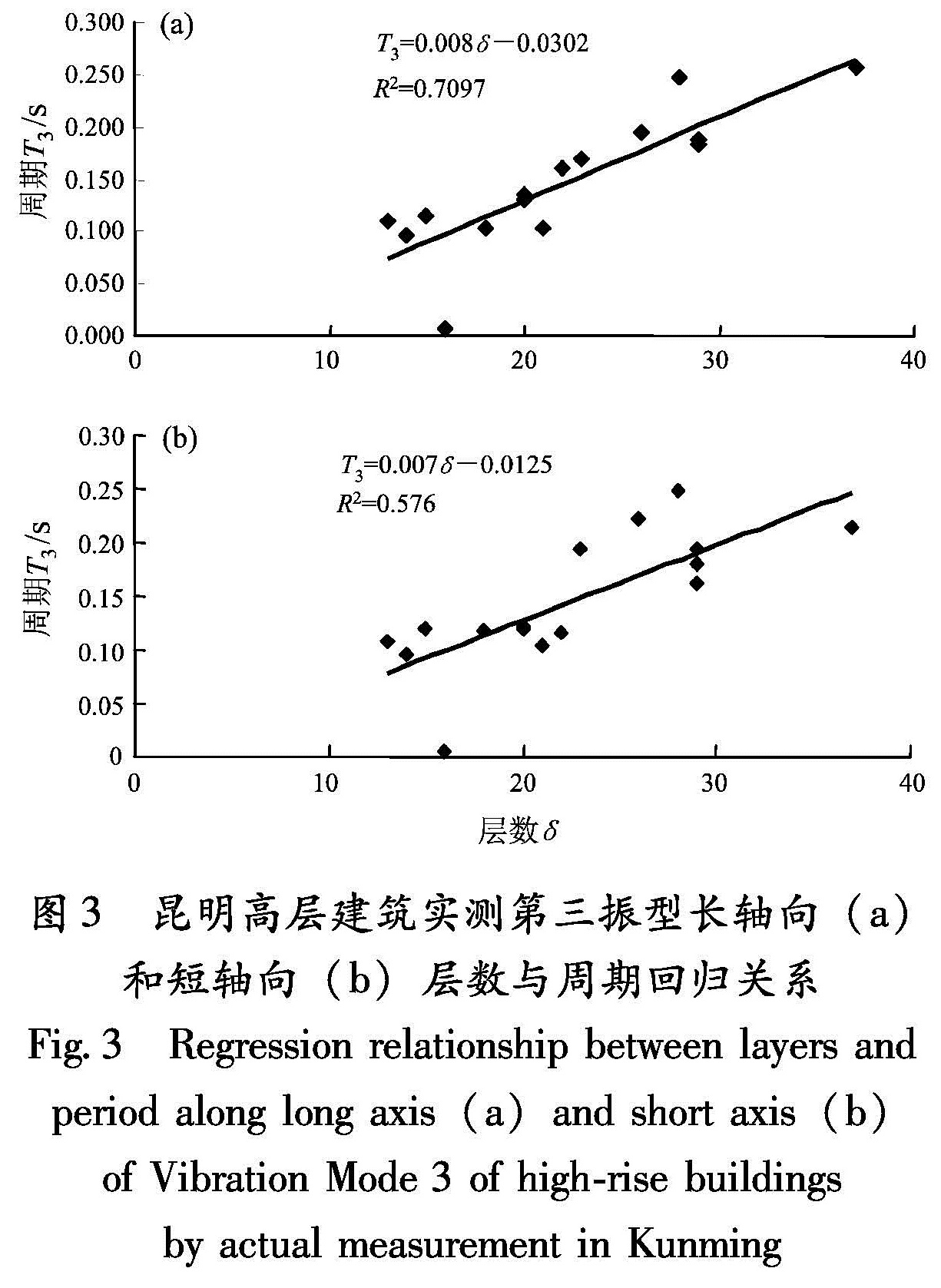
长轴:T3=0.008δ-0.0302(R2=0.7097),(21)
短轴:T3=0.007δ-0.0125(R2=0.576).(22)
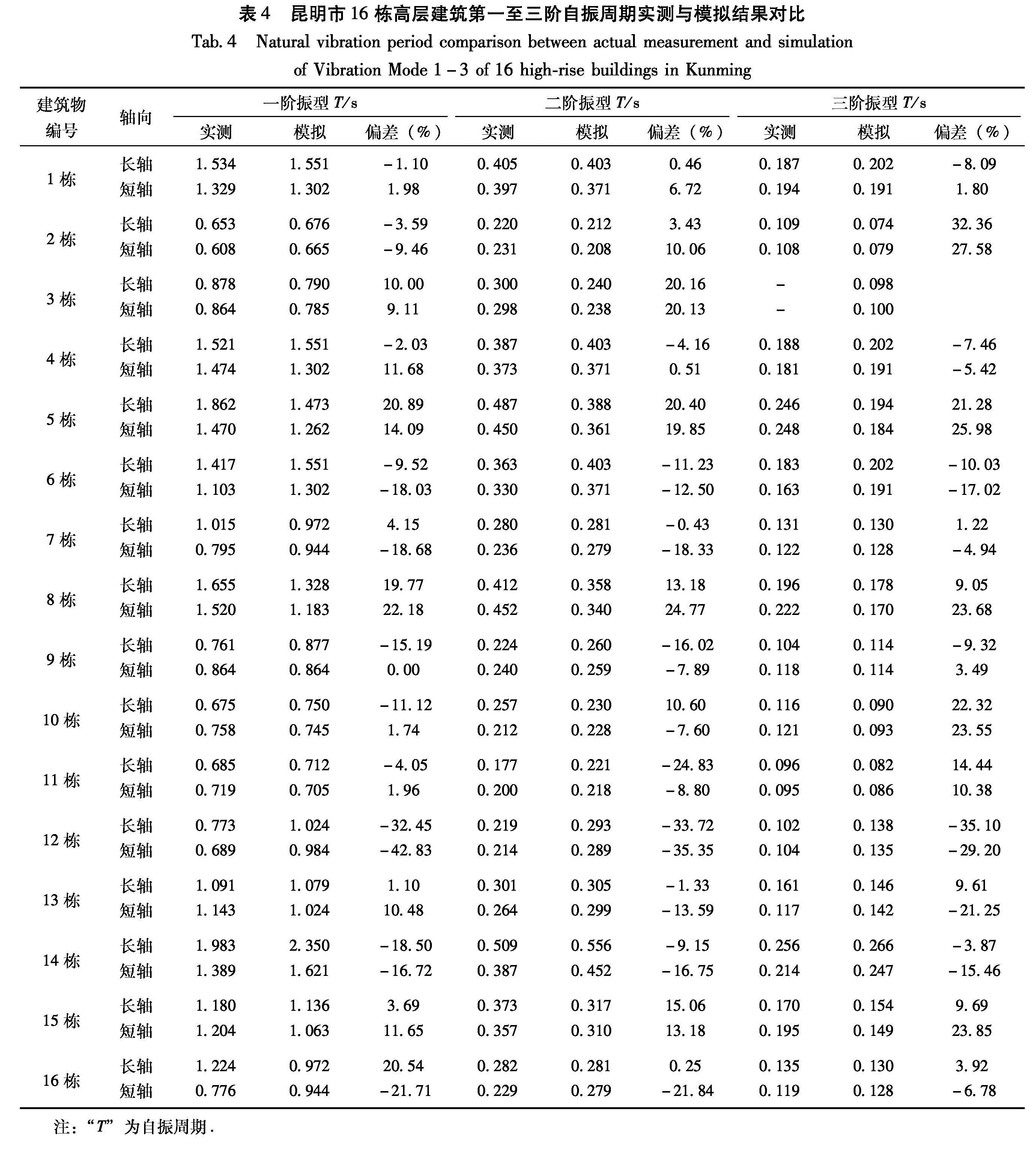
据模拟公式(17)~(22)计算得到的结果与实测结果对比见表4。
3.2 实测模拟结果分析表4为实测结果和模拟结果对比,根据这些结果,可以得出以下结论:
(1)对昆明市16栋典型高层建筑结构的实测自振周期值进行数学模拟,计算结果表明,高层建筑结构第一至第三振型模拟长、短轴周期相对正、负误差在15%内有57个,占周期总数的60.64%,表明模拟方法是可靠的。
(2)高层建筑结构第一振型模拟周期结果正、负误差在15%以内有20个,占长、短轴向周期总数的62.50%,最大误差为第12栋高层建筑短轴向周期误差(-42.83%); 第二振型模拟周期结果正、负误差在15%以内有20个,占长、短轴向周期总数的62.50%,最大误差为第12栋高层建筑短轴向周期误差(-35.35%); 第三振型模拟周期结果正、负误差在15%以内有17个,占长、短轴向周期总数的56.767%,最大误差为第12栋高层建筑长轴向周期误差(-35.1%)。
图2 昆明高层建筑实测第二振型长轴向(a)和短轴向(b)层数与周期回归关系
Fig.2 Regression relationship between layers and period along long axis(a)and short axis(b)of Vibration Mode 2 of high-rise buildings by actual measurement in Kunming图3 昆明高层建筑实测第三振型长轴向(a)和短轴向(b)层数与周期回归关系
Fig.3 Regression relationship between layers and period along long axis(a)and short axis(b)of Vibration Mode 3 of high-rise buildings by actual measurement in Kunming注:“T”为自振周期.表4 昆明市16栋高层建筑第一至三阶自振周期实测与模拟结果对比
Tab.4 Natural vibration period comparison between actual measurement and simulation of Vibration Mode 1-3 of 16 high-rise buildings in Kunming(3)第12栋高层建筑第一至第三振型模拟周期结果短轴向周期均出现-35%~45%的误差,主要原因可能是第12栋高层结构在正交中心线方向均布置了较多剪力墙,所以两个方向刚度较大,但如此布置未能形成有效抗扭转刚度,从理论计算结果表明,扭转方向周期1.33 s成为第一振型,可能抑制正常的长、短轴向的周期,导致误差较大。
根据表3理论计算结果模拟得到第一至第二振型的长、短轴方向自振周期关系曲线见图4~5; 模拟公式(23)~(26)。
第一振型
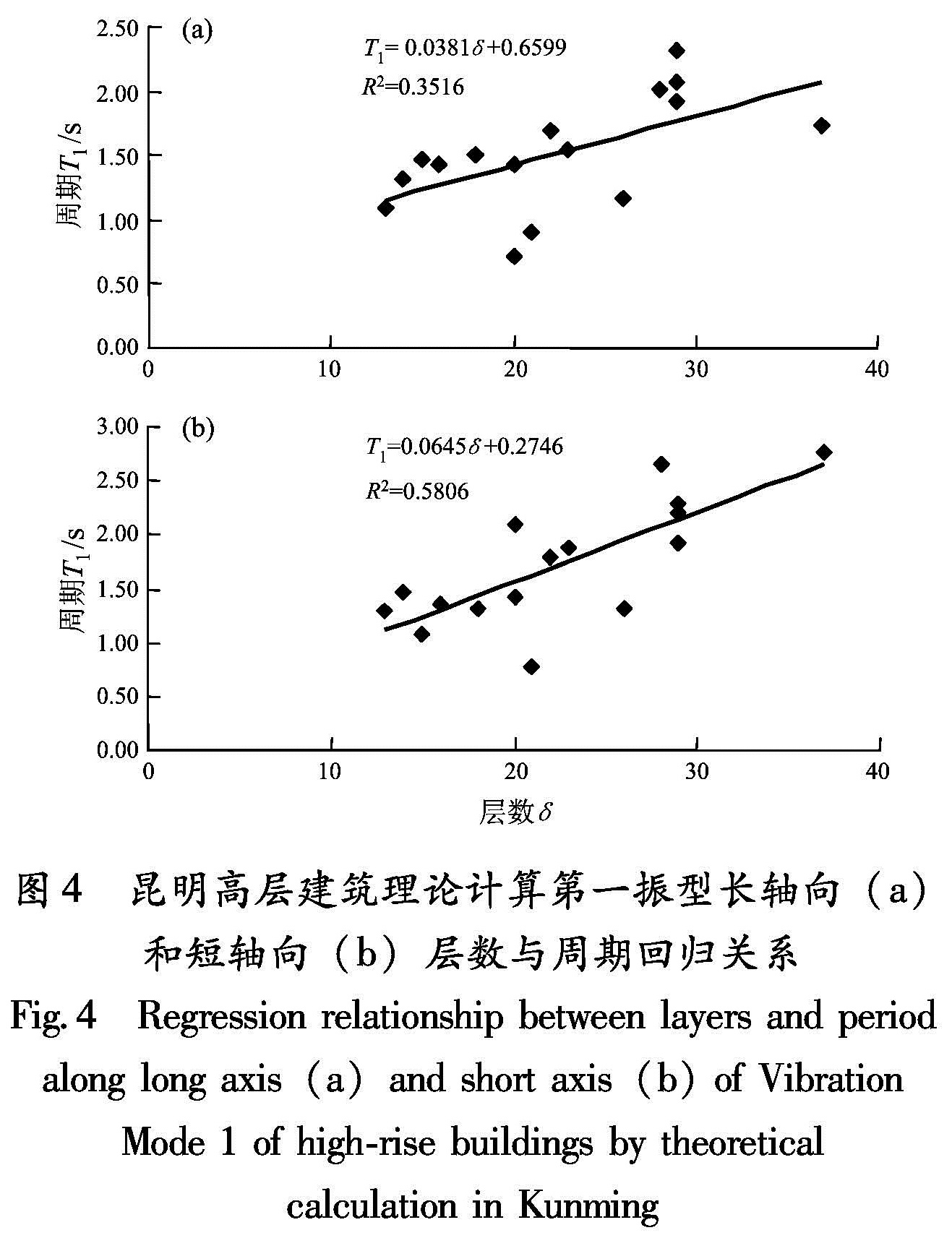
长轴:T1=0.0381δ+0.6599(R2=0.3516),(23)
短轴:T1=0.0645δ+0.2746(R2=0.5806).(24)
第二振型:
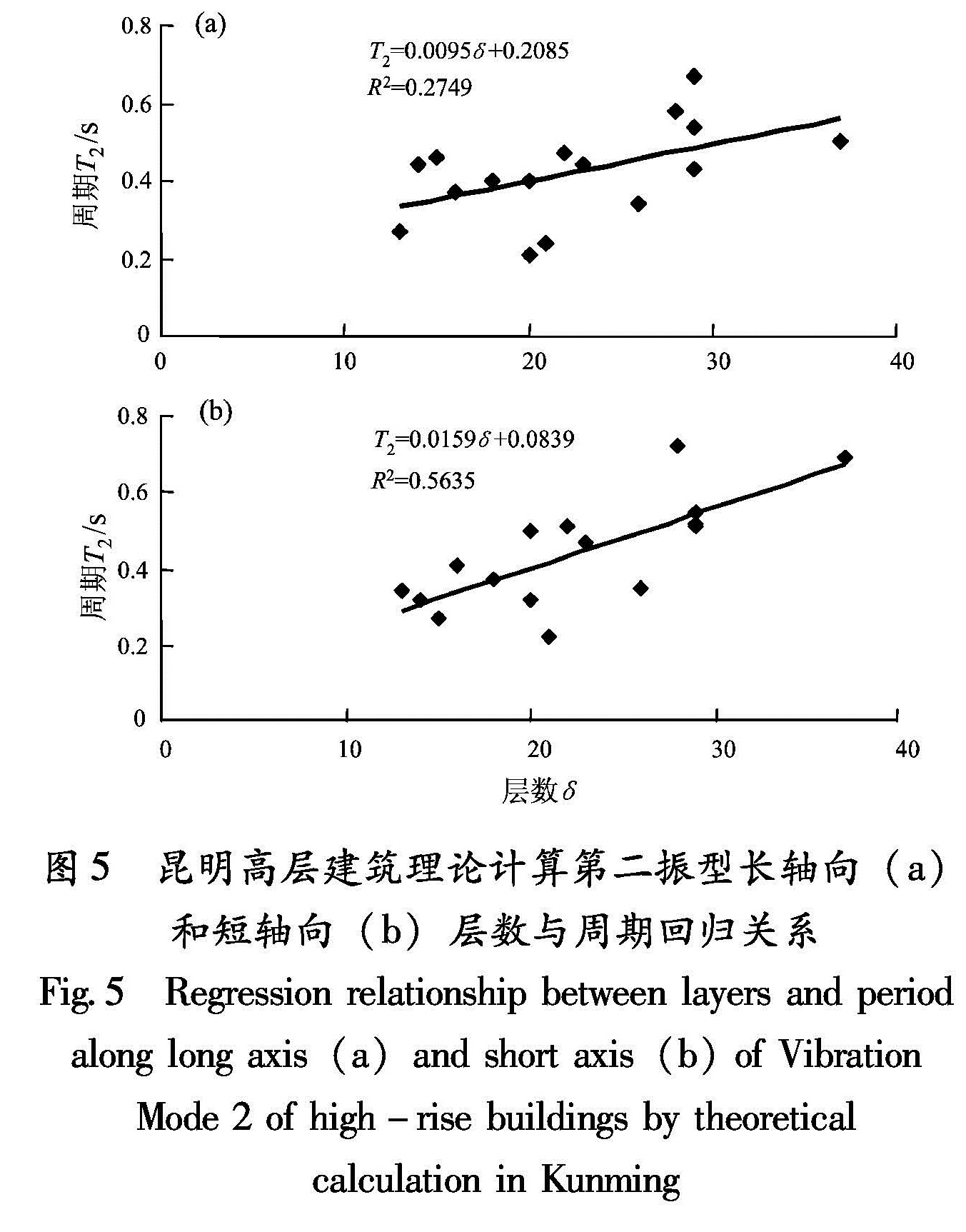
长轴:T2=0.0095δ+0.2085(R2=0.2749),(25)
短轴:T2=0.0159δ+0.0839(R2=0.5635).(26)
图4 昆明高层建筑理论计算第一振型长轴向(a)和短轴向(b)层数与周期回归关系
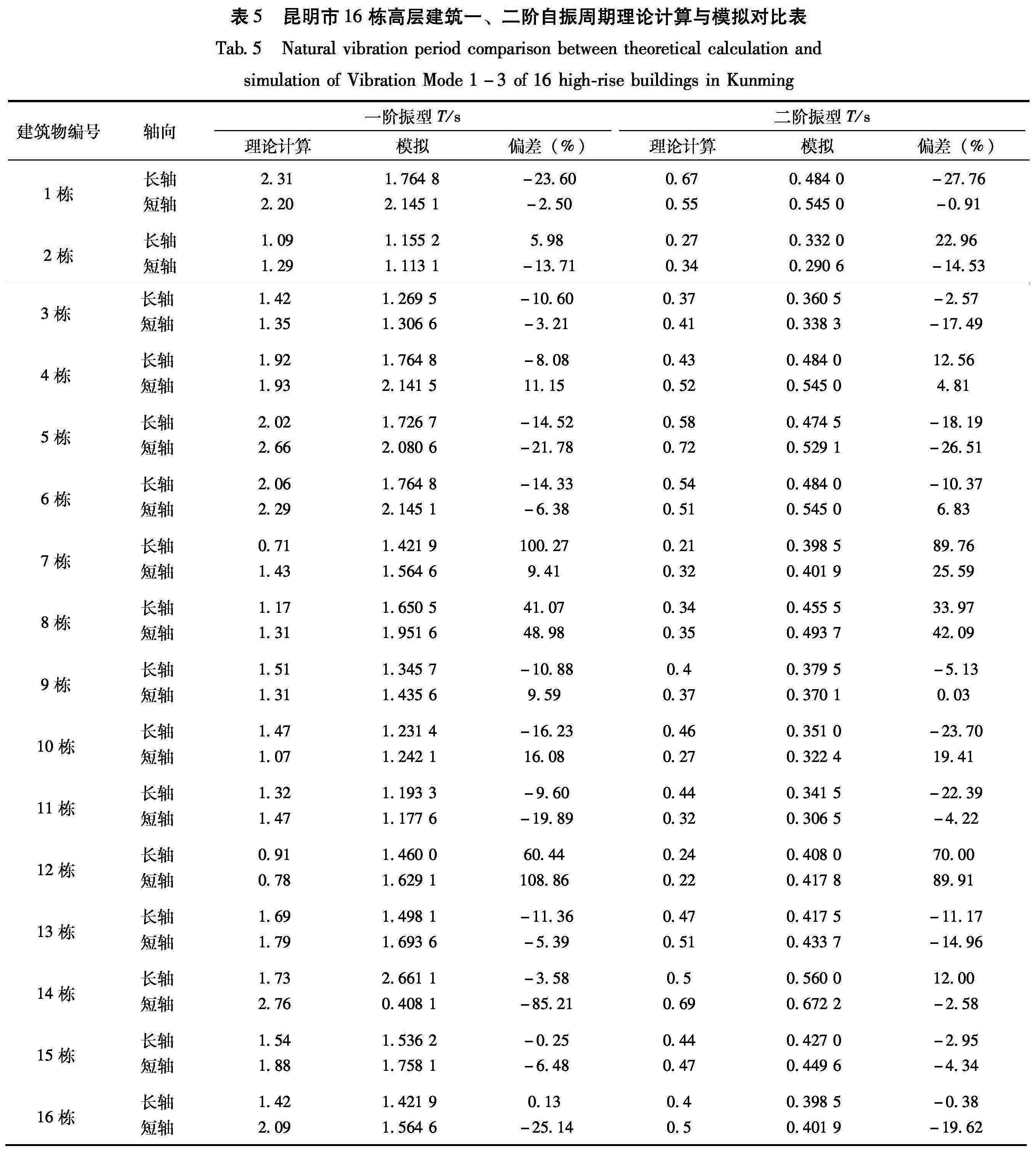
Fig.4 Regression relationship between layers and period along long axis(a)and short axis(b)of Vibration Mode 1 of high-rise buildings by theoretical calculation in Kunming3.3 理论计算模拟结果分析表5为理论计算结果与模拟结果对比,从这些结果中可以看出:
(1)对昆明16栋高层建筑结构的理论计算自振周期进行数学模拟,模拟自振周期公式计算结果多数相对正、负误差在15%以内,说明模拟方法是可靠的。
(2)高层建筑结构第一振型模拟长轴向周期除第7栋误差为100.27%、第8栋误差为41.07%和第12栋误差为60.44%外,其余各栋长轴向周期正、负误差均在23%以内,占81.25%; 第一振型模拟短轴向周期除第8栋的误差为48.98%、第12栋误差为108.86%和第14栋的误差为-85.21%外,其余各栋短轴向周期正、负误差均在25%以内,占87.5%。第二振型模拟长轴向周期除第7栋误差为89.76%、第12栋误差为70.00%外,其余各栋正、负误差均在34%以内,占87.5%; 第二振型模拟短轴向周期除第8栋误差为42.09%、第12栋误差为89.91%外,其余各栋正、负误差均在27%以内,占87.5%。
(3)第7栋高层建筑第一和第二振型模拟长轴向周期结果误差分别达100.27%和89.76%; 第12栋高层建筑第一和第二振型模拟短轴向周期结果误差分别达108.86%和89.91%。从表5中可以看到,第7栋第一和第二振型长轴向和短轴向自振周期差别较大,说明两个方向刚度分配不尽合理,可能抑制正常的长、短轴向的周期,导致误差较大(皇甫岗等,2009); 第12栋高层模拟结果误差大的原因在实测结果中已分析。
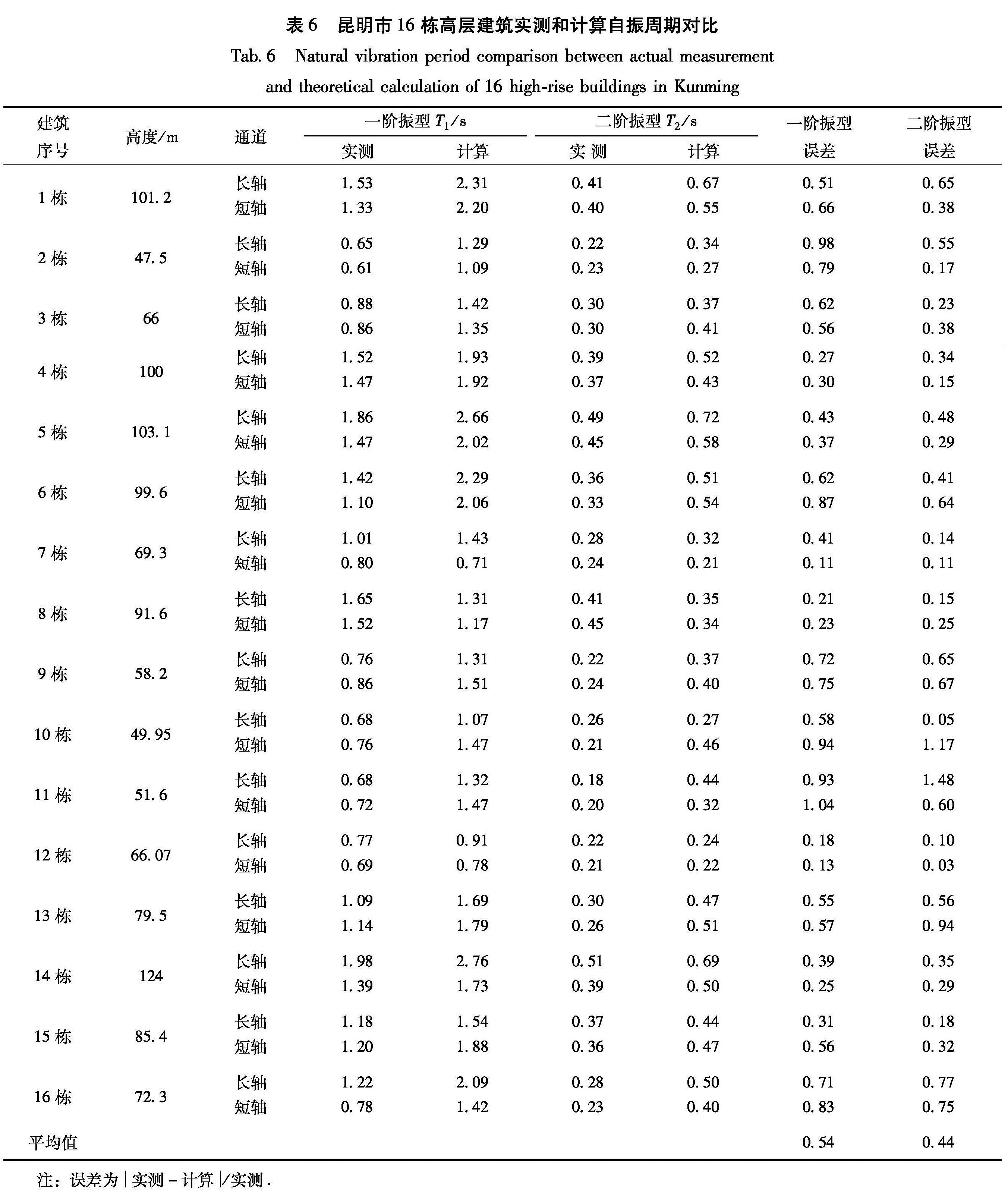
3.4 实测和理论计算结果分析从表6的对比结果看,16栋高层建筑结构第一振型周期计算结果比实测结果平均大54%,第二振型周期计算结果比实测结果平均大44%。该结果可供结构地震反应分析和抗震设计周期调整时参考。
注:误差为|实测-计算|/实测.4 结语
(1)昆明高(超高)层建筑实测与模拟公式计算结果可见(表4), 第一振型长短轴模拟周期结果正、负误差在15%以内有20个,占长、短轴向周期总数的62.50%,最大误差为第12栋高层建筑短轴向周期误差-42.83%; 第二振型长短轴模拟周期结果正、负误差在15%以内有20个,占长、短轴向周期总数的62.50%; 最大误差为第12栋高层建筑短轴向周期误差-35.35%; 第三振型长短轴模拟周期结果正、负误差在15%以内有17个,占长、短轴向周期总数的56.767%,最大误差为第12栋高层建筑长轴向周期误差-35.1%。
(2)对昆明高(超高)层建筑理论计算自振周期结果进行模拟公式计算周期结果可见,第一振型长轴向周期正、负误差在24%内有13个,占总数的81.25%,短轴向周期正、负误差在26%内有13个,占总数的81.25%; 第二振型长轴向周期正、负误差在34%内有14个,占总数的87.5%,短轴向周期正、负误差在27%内有14个,占总数的87.5%。
(3)实测模拟误差较大的第12栋高层和计算结果模拟误差较大的第7栋和第12栋,都有一个共性,即刚度分布不均匀; 而计算结果模拟误差较大的第8栋则刚度和质量都适中,但出现较大的误差,其原因有待下一步探讨。
(4)16栋结构的实测自振周期和理论计算自振周期模拟公式结果多数相对正、负误差在11%~15%,说明所得模拟公式是可靠的。模拟公式可供城市高(超高)层建筑第一至第三振型自振周期的估算、建筑抗震设计和建筑抗震性能分析等工作中,从而减化高层建筑实测和理论计算各振型自振周期的烦琐工作。
典型高层建筑的振动测试工作范围:北起昆明卷烟厂科技大楼,南至桂花大厦,东起恒丰大厦,西至云南汽车厂高层住宅楼,包含昆明市城区、高新技术开发区。
在31栋高层建筑结构中选择了具有代表性的16栋高层建筑进行建筑环境振动测试,从13层到37层不等,其中有15栋为钢筋混凝土框架-剪力墙结构,1栋为框架-筒结构(表1)。
2.1 现场观测此次观测采用美国Kinematrics公司最新生产的5台K2型高动态固态数字强震动记录仪。该仪器可选择自动或人工触发,以及定时触发与定记录长度等多种方式,触发带宽0.1~12.5 Hz,采样率100~250 sps,测量范围±2 g。
为了观测记录昆明高层建筑振动特性,仪器
灵敏度由原来的1.25 V/g,调至10 V/g,放大8倍,以满足记录要求。
2006年3~5月,云南省防灾研究所项目组先后对16栋高层建筑进行了环境振动(脉动)测试。测试时间选择在噪声较小的夜间进行,每栋建筑测试5次,分别在凌晨1~5时每隔1 h测一次,每次记录10 min。每幢建筑在进行特性观测时,仪器分别放在自由地表和各个选择楼层处。由于仪器原因11栋和1栋楼的部分测点无记录:11栋的13楼1时,1栋的1楼3时、1楼4时、1楼5时、10楼4时、10楼5时、16楼3时、16楼4时、16楼5时、18楼4时、18楼5时、22楼4时、22楼5时、24楼5时、28楼4时、22楼5时和自由地面的3、4、5时。
通过环境振动测试,了解昆明市16栋典型高层建筑结构的动力特性,包括自振频率、振型及阻尼比(王广军,樊水荣,1988)。
2.2 分析方法和数据处理2.2.1 理论基础一般来说,任何一栋建筑结构可看作是一个多自由度系统,振动测试中所记录的数据是系统对输入信号的反应,即系统输出信号。从系统识别的角度来看,即为系统输入未知,仅利用系统的响应信号来确定系统参数。这样处理问题符合
真实的情况,还可提高信号处理后的信噪比(宝志雯,1989,朱长春等,1999; 任伟新,2001; 温瑞智等,2006)。
根据线性多自由度系统动力分析理论,动态方程可用正则坐标写成如下的形式:
Y ··j(t)+2ωjξjY ·j(t)+(kj)/(mj)Yj(t)=(fj(t))/(mj).(1)
式中,ωj,kj,mj,fj(t)及ξj分别为第j振型的频率、正则化刚度、质量、外力和阻尼比。在第k个自由度上真实的响应为
Vk(t)=∑nnφkYn(t).(2)
其中,n是自由度数; nφk是正则化振型矢量; Yn(t)是模态幅值。
将时间域的响应变换到频率域,则有
nGy(ω)=|Hn(iω)|2nG f(ω).(3)
式中, nG f(ω), nGy(ω)分别为fn(t), Yn(t)的自谱。 若在第K点真实响应信号的自谱考虑为一个多输入、单输出的系统,由式(2)可得
GVK(ω)=∑m∑nmφKnφKHm(-iω)Hn(iω)mnG f(ω).(4)
对于小阻尼的结构,通常认为正则振型相互之间是不相关的,即m≠n时,Ym(t)与Yn(t)不相关,式(4)可简化为
GVK(ω)=∑nnφ2K|Hn(iω)|nG f(ω).(5)
如果系统的固有频率相互之间能很好地区分开,即当频率等于某一固有模态频率时,这个固有振型占主要成分,而其他振型分量可以被忽略。这样,GVK(ωm)可以进一步简化为
GVK(ωm)= mφ2K|Hm(ωm)|2mG f(ωm).(6)
因此,从GVK(ω)占优势的峰值位置可以找出系统的固有频率。依据不同位置GVK(ω)的比值可以给出振型,并可以用半功率点法估计振型的阻尼比。
由于自谱不包含相位信息,所以为了确定某个振型两个位置之间运动的方向,就需要用互谱的信息。第k个和第l个振型的互谱可表示为
GVkl(ω)=∑m∑nmφknφlHm(-iω)Hn(iω)mnG f(ω).(7)
同自谱计算一样,互谱在某个固有频率可简化为
GVkl(ωm)=mφkHm(-iωm)mφlHm(iωm)G f(ωm)
=CVkl(ωm)+iQVkl(ωm).(8)
式(8)可用幅值和相位的形式表示,即
GVkl(ωm)=|GVkl(ωm)|e-iθVkl(ωm).(9)
式中,|GVkl(ωm)|=(CVkl(ωm)+QV2kl(ωm))1/2, θVkl(ωm)=tan-1(QVkl(ωm))/(CVkl(ωm)).
相位角θVkl(ωm)在0°~180°间。当 mφkmφl项为正时,相位角在0°附近,这说明两点的位移是同向的; 当 mφkmφl项为负时,相位角在180°附近,说明两点的位移是反向的。
在频率域中进行动态参数估计时,其可靠性和精度主要取决于3个方面:(1)信噪比,当真正响应信号很低时,这些信号可能被噪声歪曲,甚至淹没在噪声中;(2)实际情况与假设之间的差异程度,如输出的性质、小的模态阻尼等;(3)数据分析过程的合理性,如选择合适的频带宽,数据窗、足够的平均次数等。
2.2.2 结构模态参数计算假设xi(i=1,2,…,M)是一采集的离散环境振动数据,其中M为离散点数。通常xi持续时间较长,在几十秒至几百秒之间,对其进行分析时,通过加窗截断获取分析所需长度的数据。加窗截断等效于将原信号数据xi乘以一窗函数di,设截断所得的离散数据为yi,则有
yi=xi×di.(10)
为了提高结构自振特性确定精度,降低窗的边瓣泄能效应,笔者采用了Hanning窗,即
di=1/2[1-cos((2πi)/(N-1))],0≤i≤N-1.(11)
此外,为能采用快速傅里叶算法FFT(Fast Fourier Transform)计算yi的频谱,N取为2的幂次方。
笔者采用频率域分析方法确定高层结构的自振特性,首先计算测点环境振动信号yi的傅里叶振幅谱|Y(ω)|及功率谱S(ω),然后从|Y(ω)|或S(ω)峰值确定结构的固有频率。由测点的傅里叶振幅谱|Y(ω)|及功率谱S(ω)的峰值确定这一测点的振型幅值,一旦获得该结构所有测点的振型振幅,即可确定出结构的振型。
(1)固有频率
无论是一个测点信号的自谱还是两个测点信号的互谱,在结构物固有频率的位置都会出现陡峭的峰值,在测试时的一些局部干扰也会产生一些峰值。因此,实测数据分析的主要问题是从谱中出现的所有峰值中找出真正的固有频率。一般来说,通过研究合理分布的各点的记录,确定固有频率并不困难,正常情况下,固有频率的峰点将出现在所有的谱上或至少出现在大多数的记录信号中。
(2)振型幅值
在确定结构固有频率后,用不同测点在固有频率处响应的比值,就可确定结构的振型。无论是从自谱的幅值比,还是从传递函数的幅值来确定振型幅值,从数学公式上看是一样的。但当有噪声存在时,采用多次平均得到的互谱与自谱之比的精度更高。通常在信号分析中选用相对比较的信号,对于结构物的第一、二振型具有较高的信噪比,因此,两种分析方法得到的结果十分接近。对于结构两测点间相位差的信息,可通过互相关函数Rxy(τ)来确定。为了计算互相关函数Rxy(τ),首先对环境振动信号在振型频率附近进行窄带滤波,然后,计算互相关函数Rxy(τ)。当零滞时互相关函数Rxy(0)>0,表示两测点同相,相应的振型具有相同的符号; 当零滞时互相关函数Rxy(0)<0,表示两测点相位差,相应的振型幅值符号相反(皇甫岗等,2009; 温瑞智等,2006)。
(3)阻尼比
由于自谱和互谱包含了有关振型和频率响应函数的信息,可依据自谱或互谱采用半功率点的方法计算阻尼比:
ξi=(Bm)/(2fm).(12)
式中, Bm是与第j振型有关的谱峰值的半功率点带宽。
2.3 实测结果根据每栋高层结构的测试结果,采用上述方法计算其频谱参数,通过模态分析得到其模态参数,并对多次模态分析结果进行平均得到模态参数。表2给出16栋结构正交两个水平方向的前三阶自振周期和阻尼比。
2.4 理论计算结果笔者对16栋高层建筑结构的竣工图纸进行仔细研究,并进行三维空间计算简化,再分别计算自振特性和小震(规范反应谱输入和典型地震波输入)、中震(规范反应谱输入)和大震(规范反应谱输入、设定地震输入和典型地震波输入)的地震反应分析研究,最终得到理论计算结果值(表3)。
- 宝志雯.1989.香港高层建筑的脉动试验[M].北京:清华大学出版社.
- 非明伦,周光全,卢永坤,等.2007.宁洱6.4级地震宁洱县城现代建筑典型震害分析[J].地震研究,30(4):359-363.
- 非明伦,周光全,余庆坤,等.2007.高耸结构地震动力分析[J].地震研究,30(3):281-284.
- 皇甫岗,王彬,周光全,等.2009.昆明高(超高)层建筑中近场强震响应研究[M].昆明:云南科技出版社.
- 任伟新.2001.环境振动系统识别方法的比较分析[J].福州大学学报,29(6):80-86.
- 王广军,樊水荣.1988.建筑自振周期计算方法和实测资料手册[M].北京:中国建筑科学研究院出版社.
- 温瑞智,周正华,毛国滨,等.2006.应县木塔环境振动试验[J].地震工程与工程振动,26(4).141-145.
- 翁文波,吕牛顿,张清.1996.预测学[M].北京:石油工业出版社.
- 中国科学院数学研究所统计组.1979.常用数理统计方法[M].北京:科学出版社.
- 朱长春,何彩英,张景绘,等.1999.利用脉动试验识别结构的模态参数[J].实验力学,14(2):243-250.