基金项目:国家自然科学基金(41164002)及地震行业科研专项经费项目(200808061)联合资助.
(School of Resource Environment and Earth Sciences,Yunnan University,Kunming 650091,Yunnan,China)
seismic motion parameter; regression analysis; attenuation characteristic; Yunnan region
备注
基金项目:国家自然科学基金(41164002)及地震行业科研专项经费项目(200808061)联合资助.
根据发生在云南地区震级大于3.0级的地震资料,采用最小二乘法对该地区的峰值加速度、加速度反应谱、峰值速度、峰值位移、均方根加速度等多个地震动参数进行回归分析。结果 表明,该地区的地震动衰减关系的形态与前人的研究基本一致,但水平向差异较大; 长周期部分的离散性较大,需进一步收集资料进行研究。
Based on the M>3.0 seismic observation datum collected in recent years in Yunnan,we make regression analysis for multiple seismic motion parameters such as peak ground acceleration,response spectrums of acceleration peak,ground velocity,peak ground displacement and root-mean-square acceleration by least square method.The result shows that the seismic attenuation relation curve we obtained simulates with that of former researches,but there is great difference between them in horizontal direction.The standard deviation in long period is relatively large,which means more data should be collected in the future research.
引言
近年来,强烈地震频发,地震所造成的破坏对人们正常生产生活造成巨大影响。云南省地处印度板块与欧亚板块中国大陆碰撞带的东缘附近,新构造与现代构造运动强烈,活动断裂发育,地震灾害频繁发生。云南地震具有频度高、强度大、震源浅、分布广、灾害重的特点。同时,近十年来云南尚未发生较大震级的地震,云南省境内近期发生较大震级地震的可能性进一步加大。
地震动是引起地震灾害的外因,是地震与结构抗震之间的桥梁,是工程地震研究的主要内容,对于地震动的研究一般是对其地震动参数衰减关系的研究。地震动参数在地震危险性评价工作中起着非常重要的作用,是编制地震动区划图的重要依据,对抗震设计、城市防震减灾的研究都有着重要的现实意义(胡聿贤,1999,2006; 崔江余,杨伟毅,2002; Somerville,Graves,2006)。然而不同工程对工程场地地震安全性评价的深度以及提供的地震动参数的要求不同,这取决于工程的类型、安全性、危险性以及社会影响等因素(俞言祥,2002; 俞言祥,汪素云,2006)。比如对一般工业民用建筑,我国已经颁发的抗震设计规范都以基本烈度为基础来确定设防烈度,以烈度值换算成地震动峰值加速度进行抗震设计,但对一些重要工程和特殊工程如超高层建筑、大桥、大坝、核电厂等只提供峰值加速度还不能满足抗震设计要求,还必须提供地震过程的频率特性和强震动的持时等地动参数。
针对云南地区地震观测资料较为丰富的特点,王亚勇等(1991)、王培德等(1993)、向建光和高东(1992)、崔建文等(2006)对这个区域的地震动衰减特性进行了研究,且主要研究峰值加速度的衰减,对地震动衰减的其他参数研究较少。因此,对云南地区地震动衰减的研究,有必要对该地区多个地震动参数的衰减特性进行研究。
1 地震动参数与理论方法
1.1 地震动参数地震动的特性可以通过3个要素来描述,即振幅、频谱和持时。这3个要素的不同组合决定着各类结构物的安全。为了简单实用,本文只研究对工程抗震起主要作用的地震动参数,如下:
(1)加速度(PGA):从静力的观点看待地震动,直观地认为峰值加速度可以作为地震动强弱的标志,因为由此产生的惯性力可代表地震动对结构的破坏作用。
(2)加速度反应谱(Sa):结构物有其自振频率,假若地震动的频谱集中于低频,它将引起长周期结构物的巨大反应; 反之,若地震动的卓越频率在高频段,则它对刚性结构物的危害大。当参数y是单自由度体系的相对位移d、相对速度v、绝对加速度a时,分别称为位移反应谱Sd、速度反应谱Sv、加速度反应谱Sa,且它们的近似关系如下
Sa=(2π)/TSv=ωSv=((2π)/T)2Sd=ω2Sd,(1)
其中,
Sv(ω,ξ)=|∫0Ta(τ)e-ξω(t-τ)cos(ω(t-τ))dτ|max.(2)
式中,ω为圆频率,且ω=(2π)/T。
(3)峰值速度(PGV):峰值速度与地震动能量有关,因此它也作为地震动强弱的标志。
(4)峰值位移(PGD):峰值位移与变形有关,和峰值速度一样也作为地震动强弱的标志。
(5)均方根加速度(Arms):从随机过程观点看,加速度过程a(t)中的最大峰值是一个随机量,不宜作为地震动特性的标志,而方差则是表示振幅大小特性的一个统计特征。假若取Td为强震动阶段的持时,则地震动过程a(t)在此持时内可以近似看作是平稳过程,那么单位持时的能量与方差成正比,即
a2rms=σ2a=1/(Td)∫0Tda2(t)dt.(3)
这就是均方根加速度arms的定义,本文用Arms表示。
1.2 研究方法选择地震动衰减理论模型
lny=c1+c2M+c3ln(R+c4ec5M).(4)
其中,y为地震动的任一物理量,如峰值加速度、峰值速度、反应谱(给定周期和阻尼比的幅值)等; c1、c2、c3、c4、c5为回归系数; M为震级; R为震中距离; e=2.7183; 标准差为σlny。
在对地震动衰减关系进行回归时,一般回归的原则是使某一目标函数优化,常用的原则是回归误差最小二乘法。若已知M、R,求地震动y,则常用的回归原则是
J=∑Ni(lnyi观测-lnyi回归)2=min,(5)
标准差为
σlny=(J/N)1/2,(对于lny的标准差).(6)
在采用式(4)进行回归时,回归是非线性的,本文采用二步回归法处理。第一步先对同一震级进行回归,而分别将C0= C1+C2M与R0(M)=c4ec5M视为常数; 第二步再根据不同震级求得的C0与R0(M),求得C1与C2以及C4与C5。
2 数据资料
本文采用数据所包括的地震为:1976年的龙陵MS7.3地震、1988年的澜沧—耿马MS7.6地震、1995年的武定MS6.5地震、1996年的丽江MS7.0地震、2000年的姚安MS6.5地震、2001年的施甸MS5.9地震和永胜MS6.0地震、2006年的盐津MS5.1地震、2007年的大理MS4.4地震等。收集到的地震数据记录共有72条。
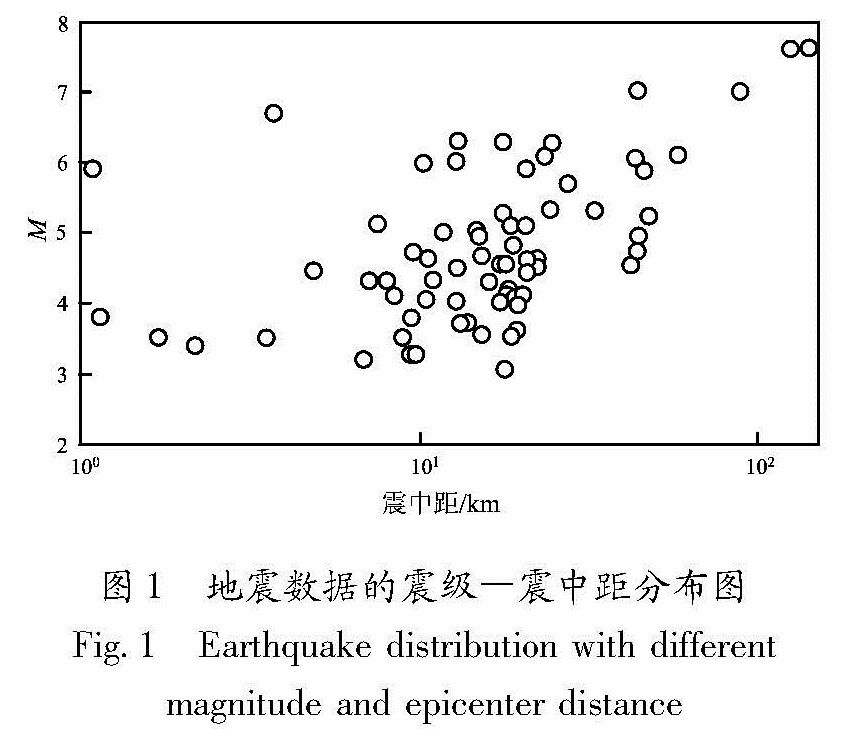
从图1的震级分布看,在3.0<M≤6.0范围的数据占绝大多数; 从震中距分布看,绝大多数的数据集中在8 km≤R≤50 km的空间范围内。地震数据表现为偏颇或分布上的不均匀性:数据主要集中分布在小震的中近场和大震的远场,而在小震的远场和大震的近场则较缺乏。说明本文的统计结果对小震的远场和大震近场参考意义不大。
3 地震动衰减关系回归
王亚勇等(1991)根据澜沧—耿马地震的强震资料拟合的地面水平向(东西向)加速度衰减公式为
lgA=2.6618+0.198M-1.175lg(R+r).(7)
王培德等(1993)根据澜沧—耿马、剑川、禄劝地震的强震资料拟合的地面水平向峰值加速度衰减公式为
lgAmax=2.29+0.38MS-1.97lg(R+10).(8)
向建光和高东(1992)根据禄劝、澜沧—耿马地震所取得的强震观测资料,并结合美国西部的强震资料拟合出的基岩水平向峰值加速度衰减公式为
Ap=1291.07e0.5275MS(R+15)-1.5785.(9)
崔建文等(2006)根据禄劝、澜沧—耿马、武定、丽江、剑川、宁蒗、姚安、施甸以及永胜地震等地震的主、余震所取得的强震观测资料拟合出地面水平向峰值加速度衰减公式为
lgAmax=3.5549+0.2881M+(-2.7317+0.0889M)·lg(R+13),σ=0.5314.(10)
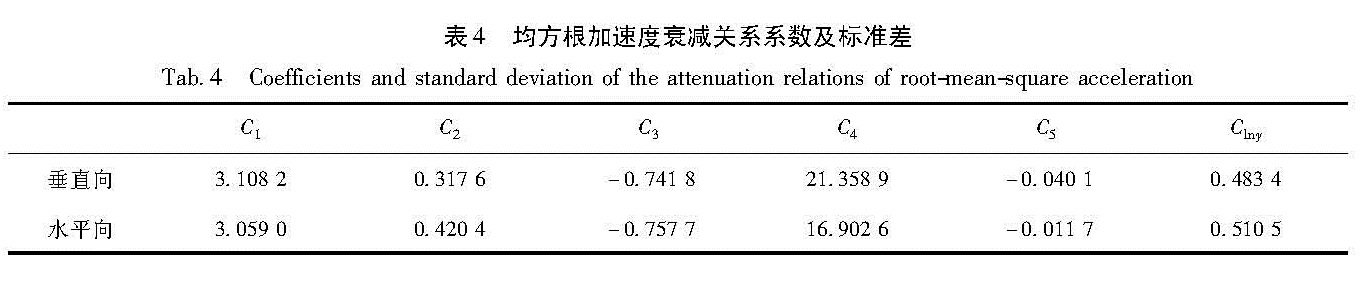
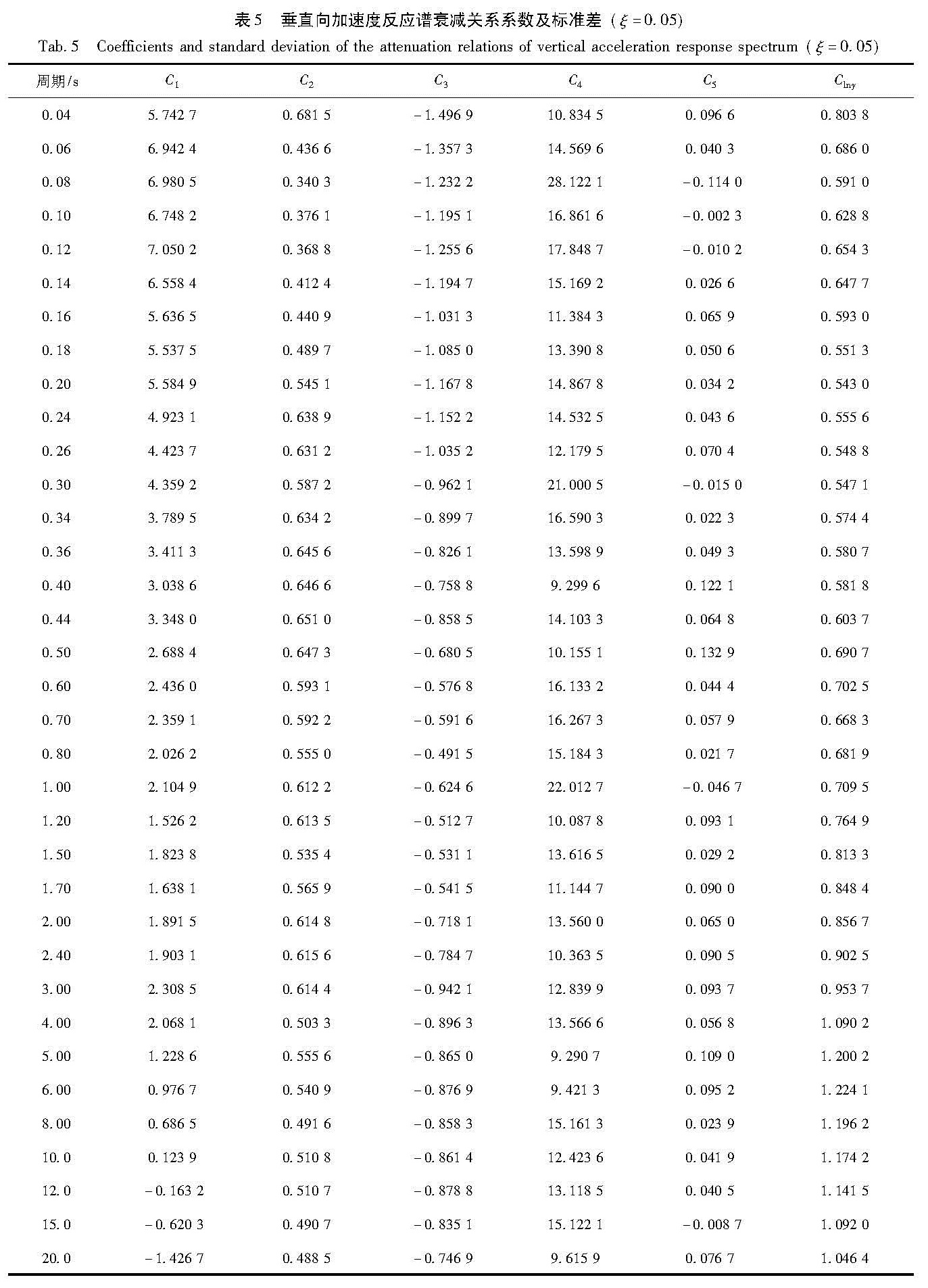
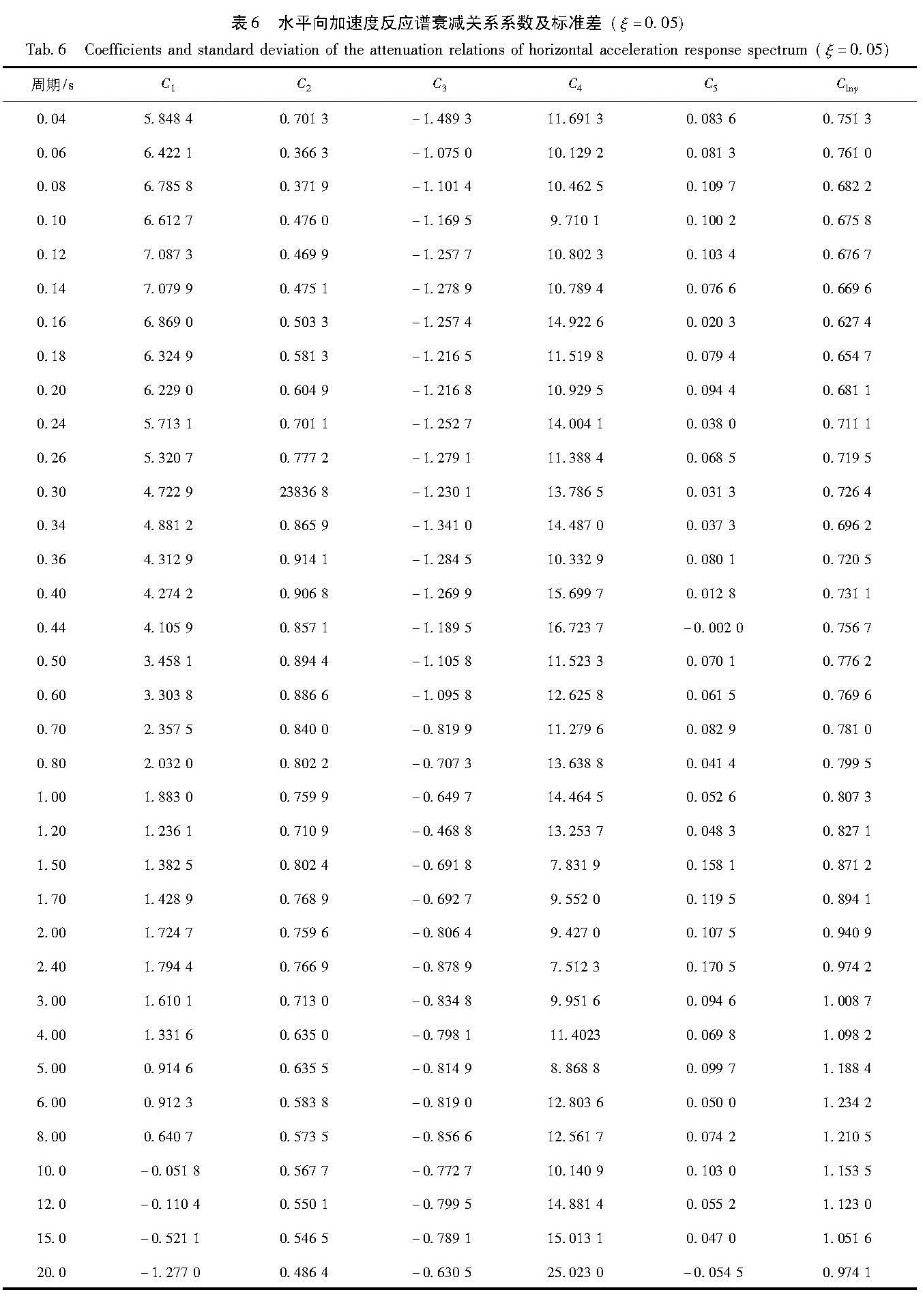
3.1 衰减关系系数及标准差应用式(4)~(6)可求得多个地震动参数水平向和垂直向衰减关系系数及标准差(水平向取两水平方向的较大值)。表1~6分别为峰值加速度、峰值速度、峰值位移、均方根加速度、垂直向加速度反应谱、水平向加速度反应谱衰减关系系数及标准差。
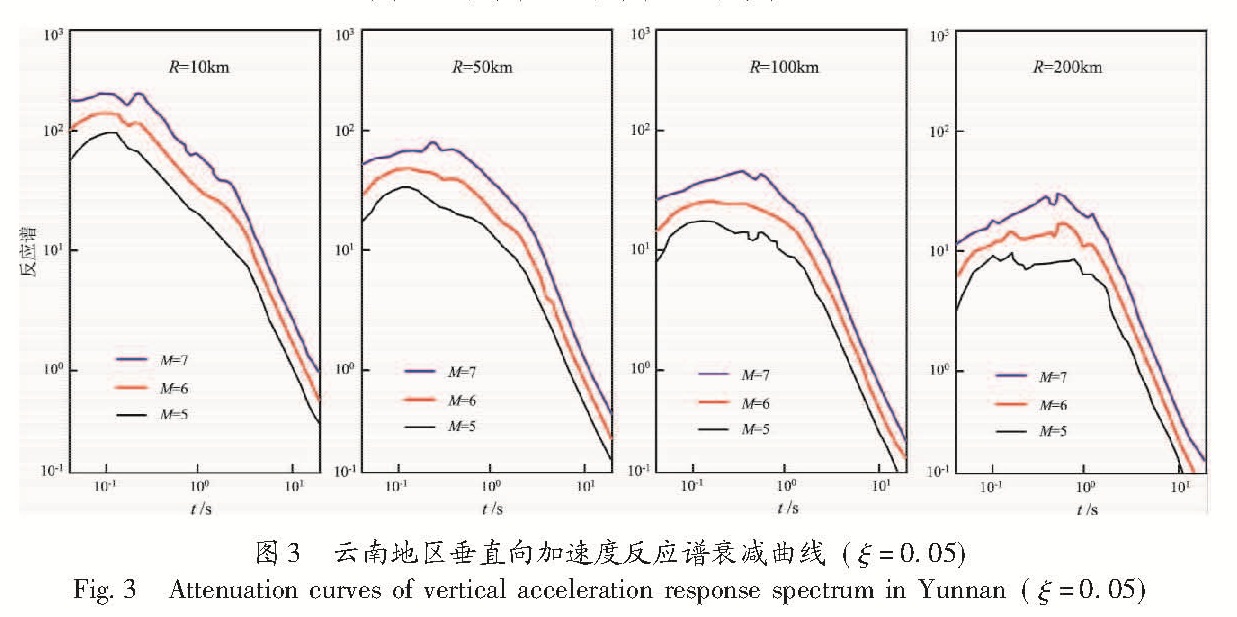
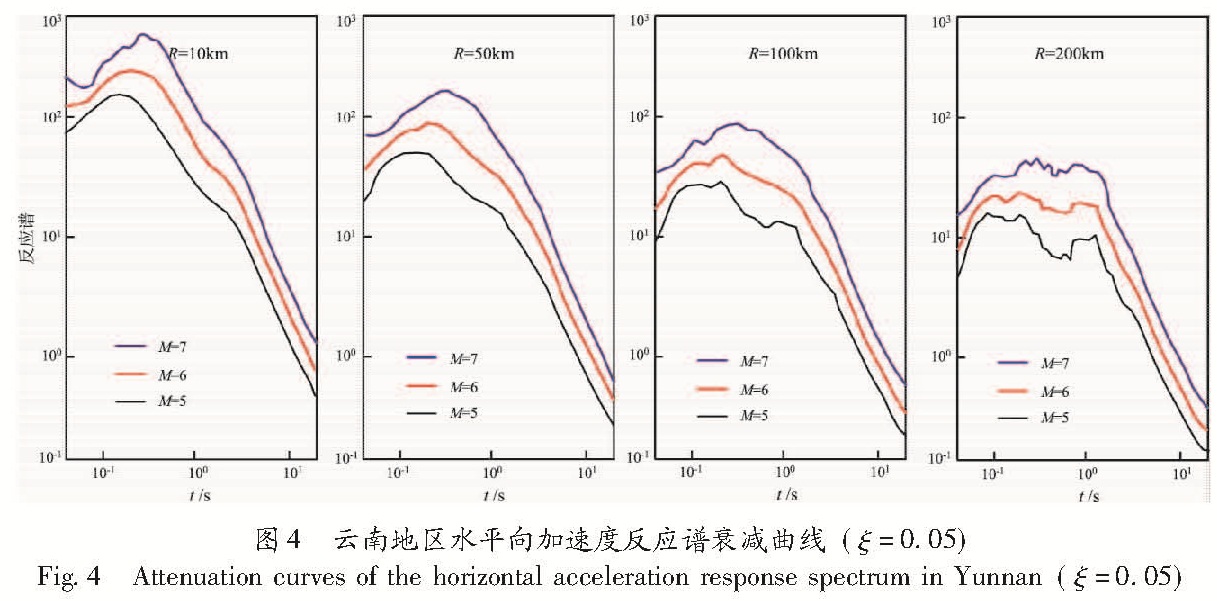
3.2 对比与分析应用上面的计算结果,可画出多个地震动参数的衰减曲线(图2~4)。从图2可看出,峰值加速度衰减较快(图2a),而峰值位移衰减相对较慢(图2c),这与统计资料中有远场大震资料是相符的。图3及图4分别表示不同震级与不同震中距处,垂直和水平向反应谱曲线,体现出近场以短周期的地震波为主导,远场以长周期的地震波为主导的特征,与地震波的衰减规律是相符的。
表1 峰值加速度衰减关系系数及标准差
Tab.1 Coefficients and standard deviation of the attenuation relations of peak ground acceleration表2 峰值速度衰减关系系数及标准差
Tab.2 Coefficients and standard deviation of the attenuation relations of peak ground velocity表3 峰值位移衰减关系系数及标准差
Tab.3 Coefficients and standard deviation of the attenuation relations of peak ground displacement表4 均方根加速度衰减关系系数及标准差
Tab.4 Coefficients and standard deviation of the attenuation relations of root-mean-square acceleration表5 垂直向加速度反应谱衰减关系系数及标准差(ξ=0.05)
Tab.5 Coefficients and standard deviation of the attenuation relations of vertical acceleration response spectrum(ξ=0.05)表6 水平向加速度反应谱衰减关系系数及标准差(ξ=0.05)
Tab.6 Coefficients and standard deviation of the attenuation relations of horizontal acceleration response spectrum(ξ=0.05)图2 云南地区不同震级地震动各参数衰减曲线
(a)峰值加速度;(b)峰值速度;(c)峰值位移;(d)均方根加速度
Fig.2 Different ground motion parameters attenuation curves with different magnitudes in Yunnan(a)PGA;(b)PGV;(c)PGD;(d)RMSA图3 云南地区垂直向加速度反应谱衰减曲线(ξ=0.05)
Fig.3 Attenuation curves of vertical acceleration response spectrum in Yunnan(ξ=0.05)图4 云南地区水平向加速度反应谱衰减曲线(ξ=0.05)
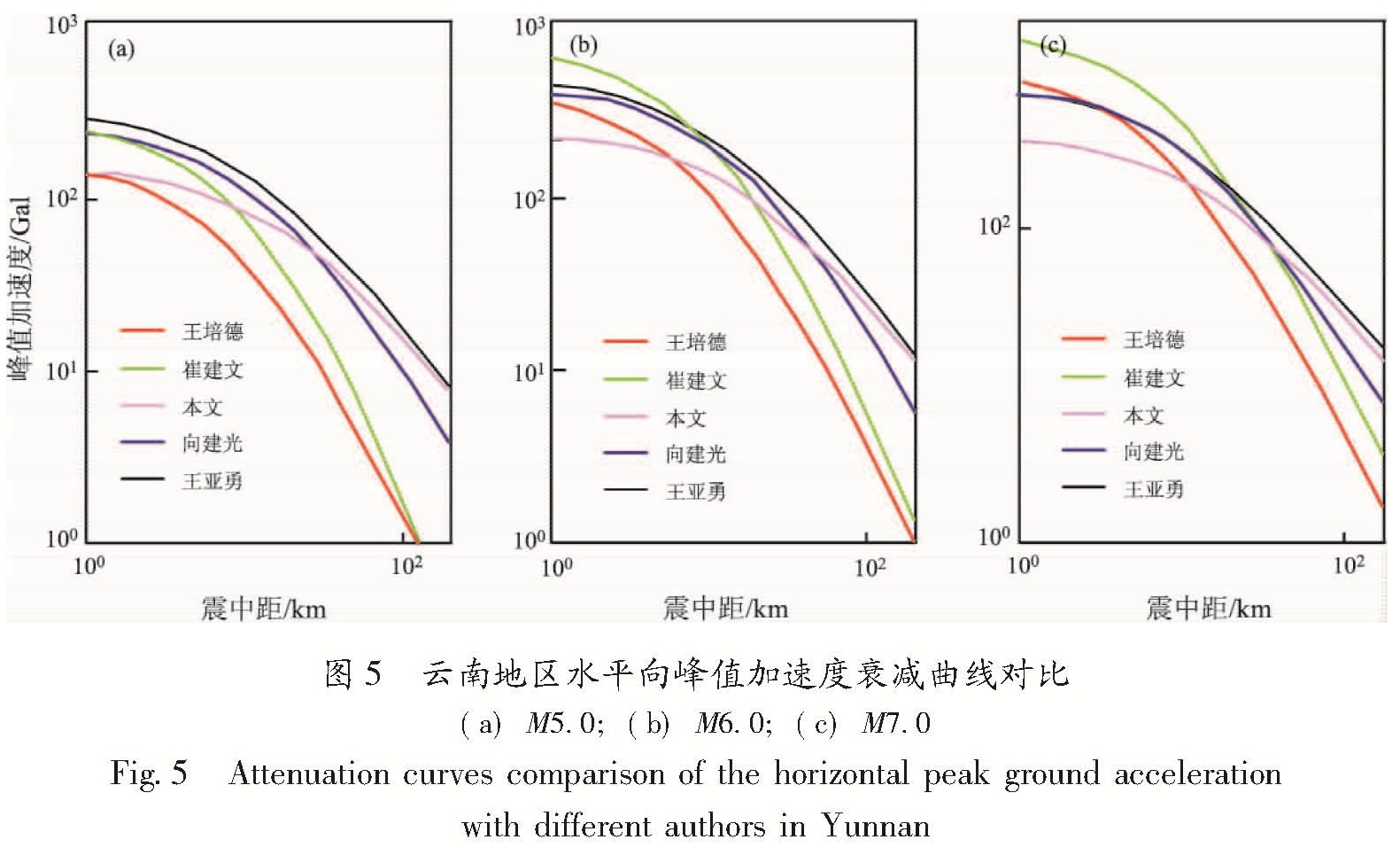
Fig.4 Attenuation curves of the horizontal acceleration response spectrum in Yunnan(ξ=0.05)图5分别是王亚勇等(1991)、王培德等(1993)、向建光和高东(1992)、崔建文等(2006)及笔者求得的云南地区水平向峰值加速度衰减曲线比较。图中表明,本文的结果在近场处的衰减比前人的结果要快,在远场处比前人的结果要慢点,基本是前人结果的包络线。
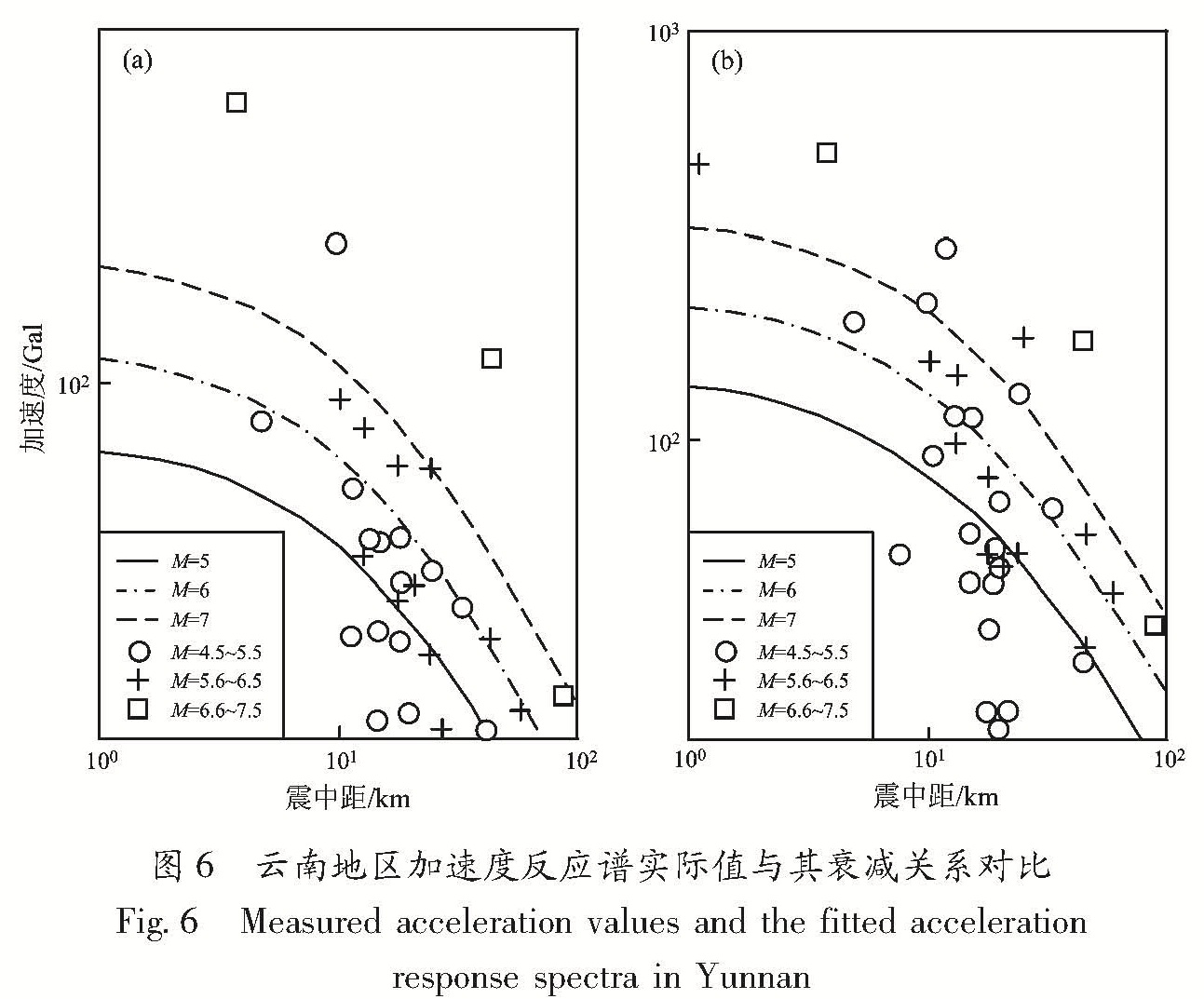
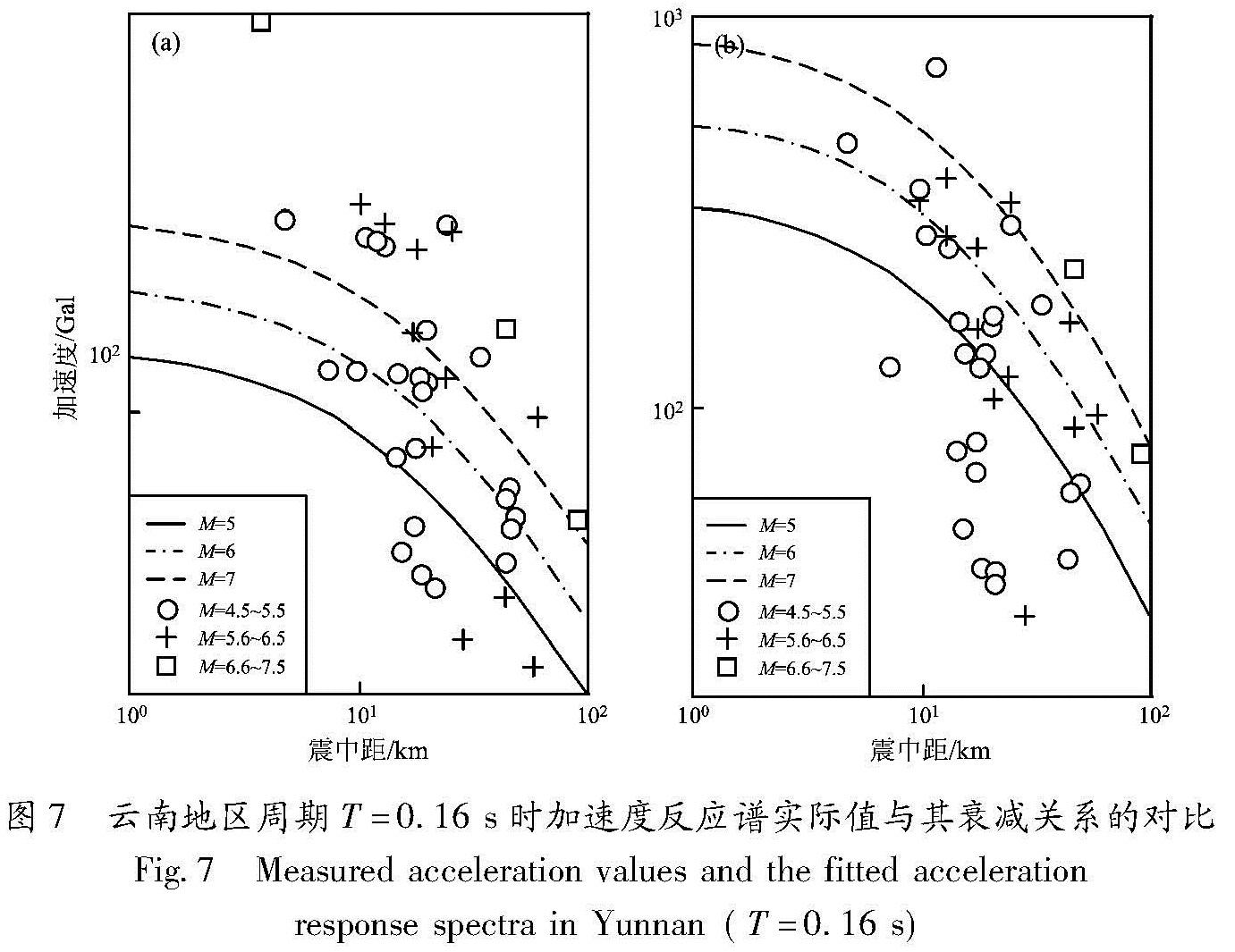
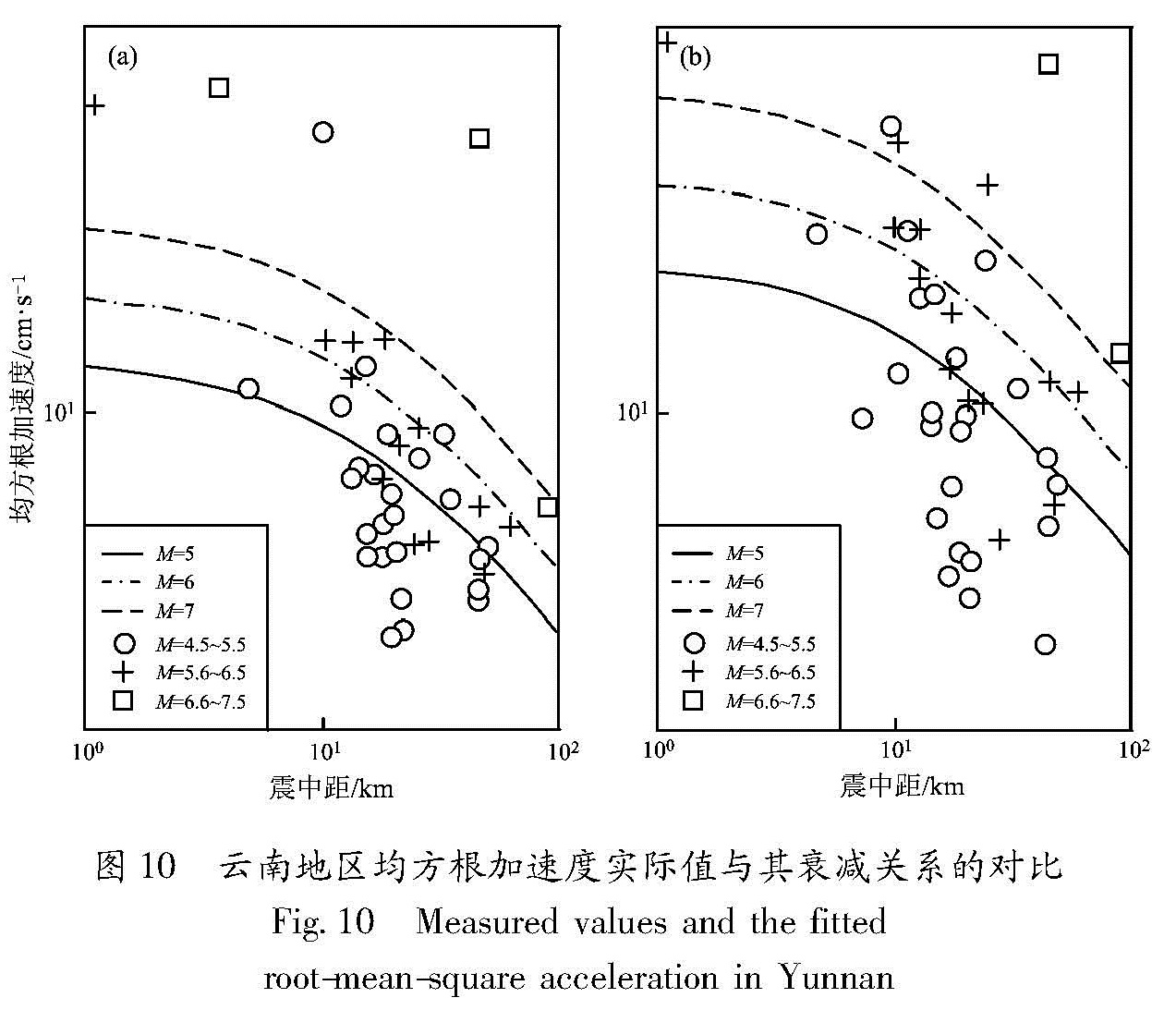
云南地区多个地震动参数实际值与其衰减关系计算值的比较见图6~10。从图6中可见,竖直向计算值较观测值大,而水平向计算结果与观测结果比较接近。图7为运用反应谱计算公式得出的值,当T=0.16 s时,垂直向的加速度计算值较观测值较小,水平向的加速度计算值较观测值接近。图8显示的峰值速度也体现出在竖直向的计算位移较观测位移偏大的结果。图9显示的峰值位移则在竖直方向与水平方向的计算结果与观测结果较吻合。图 10计算了均方根加速度,其结果也是竖直向的计算结果较观测结果偏大。从图中可以看出,垂直向的衰减关系给出的结果与实测结果分布偏差较多,而水平向的衰减关系给出的结果与实测结果分布基本合理,说明水平向的统计关系比垂直向更合理。
图5 云南地区水平向峰值加速度衰减曲线对比
(a)M5.0;(b)M6.0;(c)M7.0
Fig.5 Attenuation curves comparison of the horizontal peak ground acceleration with different authors in Yunnan图6 云南地区加速度反应谱实际值与其衰减关系对比
Fig.6 Measured acceleration values and the fitted acceleration response spectra in Yunnan图7 云南地区周期T=0.16 s时加速度反应谱实际值与其衰减关系的对比
Fig.7 Measured acceleration values and the fitted acceleration response spectra in Yunnan(T=0.16 s)由于峰值加速度与均方根加速度单位相同,因此将它们进行对比分析,见图 11。从图中可以看出,两者的衰减趋势基本相同,震级大的峰值加速度与均方根加速度间的差异更大。
4 讨论及结论
本文通过对云南地区主要地震动参数的统计分析,并与前人的研究结果进行了对比。由于地震动衰减关系具有很强的地域性,本文结果只反映了云南地区地震动衰减的一般特性,且得出的衰减关系只适用于中强震和中近场潜在震源控制的地区。
云南地区地震动参数衰减形态一致,水平向的参数较垂直向的对应参数大,并未显现出在近场垂直向地震动频率成分更丰富现象,这可能是由于本文收集到的数据大多数震中距为中等距离且震级偏小,缺乏大震; 峰值加速度衰减曲线与
图9 云南地区峰值位移实际值与其衰减关系的对比
Fig.9 Measured displacement values and the fitted peak ground displacement in Yunnan图 10 云南地区均方根加速度实际值与其衰减关系的对比
Fig.10 Measured values and the fitted root-mean-square acceleration in Yunnan已有成果的形态基本一致,但由于不同作者资料的积累或回归模型的选取不同,其衰减曲线也有相应的差别。本文收集到的数据与前人相比台次少,而且缺乏大震的近场和强震的远场资料,使回归结果在大震的近场和强震的远场方面存在着一定的外推性; 加速度反应谱衰减关系在大震级和远场时其衰减曲线光滑性较差,表现出异常的上凸或下凹,存在着一定的离散性。
将地震动参数的衰减关系应用于地震动强度危险性分析时需要很谨慎,特别是峰值位移以及加速度反应谱长周期部分,因为其标准差较大。
从多个地震动参数实际值与其对应的衰减关系对比可以看出,其衰减关系与实际资料基本上符合,只是实际资料的离散程度偏高。
均方根加速度比峰值加速度的幅值小很多,且在本文讨论范围内前者的离散程度较后者小些,
图 11 云南地区峰值加速度和均方根加速度衰减曲线对比
Fig.11 Attenuation curves comparison between the root-mean-square acceleration and the peak ground acceleration in Yunnan均方根加速度更适合应用在地震动强度危险性分析,但峰值加速度仍然是地震动衰减研究的重要参数。
因此,本文的统计结果,对水平向参数而言,针对中远场的情况,其分析结果是合理的。对于近场和垂直向的地震参数,还需要进一步收集资料进行分析。
衷心感谢云南省防灾研究所给予的帮助。
- 崔建文,李世成,高东,等.2006.云南分区地震动衰减关系[J].地震研究,29(4):386-391.
- 崔江余,杨伟毅.2002.地震动参数衰减规律的研究[J].世界地震工程,18(3):116-122.
- 胡聿贤.2006.地震工程学(第二版)[M].北京:地震出版社.
- 胡聿贤.1999.地震安全性评价技术教程[M].北京:地震出版社.
- 王培德,陈运泰,王鸣.1993.中国西南地区近震源地面运动特征[M].北京:地震出版社.
- 王亚勇,黎家佑,刘小弟.1991.澜沧—耿马强震地面运动特征研究[J].地震工程与工程振动,11(2):11-19.
- 向建光,高东.1992.云南地区基岩水平峰值加速度衰减规律[J].中国地震,8(3):32-39.
- 俞言祥,汪素云.2006.中国东部和西部地区水平向基岩加速度反应谱衰减关系[J].震灾防御技术,1(3):206-217.
- 俞言祥.2002.长周期地震动衰减关系研究[D].北京:中国地震局地球物理研究所.
- Somerville P G,Graves R W.2006.地震强地面运动的特征描述[J].国际地震动态,(3):12-18.