基金项目:国家自然科学基金资助项目(50908027)和地震工程与工程振动开放实验室资助项目(2009A10)联合资助.
(大连大学 土木工程研究与技术开发中心,辽宁 大连 116622)
(Research and Development Center of the Civil Engineering Technology,Dalian University,Dalian 116622,Liaoning,China)
Hilbert-Huang Transform(HHT); Empirical Mode Decomposition(EMD); energy distribution; predominant frequency; Wenchuan M8.0 earthquake
备注
基金项目:国家自然科学基金资助项目(50908027)和地震工程与工程振动开放实验室资助项目(2009A10)联合资助.
利用HHT方法对6个台站的汶川8.0级地震加速度记录进行EMD分解,进而对地震波输入结构的总能量进行分解,得到地震动能量在IMF分量之间的分布关系。同时通过对各分量边际能量谱的分析,可以从另一方面得到地震波的频谱特性,边际能量谱峰值频率与地震波傅立叶谱的卓越频率相同,边际能量谱也可以作为一种估算震动卓越周期的方法。
Using the Hilbert-Huang Transform,acceleration time histories recorded by 6 stations in Wenchuan M8.0 earthquake are decomposed into several Intrinsic Mode Function components by Empirical Mode Decomposition.The total energy of structure inputted by seismic wave is decomposed to get the distribution relation of the ground motion energy in the different IMF component.By analysis of marginal energy spectrum of each IMF component,we can obtain the spectral characteristics of seismic wave.The frequency of marginal energy spectrum peak is the same as the predominant period of the Fourier spectrum of seismic wave,so it can also be used as the way to estimate the predominant period of vibration.
引言
采用恰当的数据分析方法,从地震记录中提取地面运动特性是非常重要的:作为模拟地震动的输出和地震现象的解释,有助于对地震震源机制、在非线性土壤中传播等问题的理解; 作为岩土和结构工程系统的输入,可以用来计算结构的动力非线性反应,从而评估结构的抗震性能。
传统的地震记录分析方法,如傅立叶谱分析对地震记录等非平稳数据分析会产生扭曲或者信息记录不完全等问题(Zhang et al,2003)。Huang等(1998,1999)提出了将经验模态分解(Empirical Mode Decomposition,简称EMD)与著名的Hilbert谱分析相结合,形成了一种新的数据处理方法,称之为希尔伯特-黄变换(Hilbert-Huang Transfrom,简称HHT)。HHT方法是专为非线性、非平稳数据分析所设计,EMD是HHT方法的关键部分,任何复杂的数据都可以通过EMD分解成有限的、少量的固有模态函数(Intrinsic Mode Function,简称为IMF)。HHT方法已经引起了工程和科研领域的广泛关注(公茂盛等,2007,2010; 鞠萍华等,2009; 祁克玉等,2010; 王彬等,2005; 周挚等,2005; Duffy,2004; Li et al,2005; Jia et al,2009; Jiang,Yan,2008; Ortega,Smith,2009; Zhang et al,2003)。
地震对结构的作用本质上是能量的传递、转换和耗散的过程,当地震动输入结构的能量小于结构的耗能能力时,结构是安全的,反之结构将会破坏,因此,对地震输入能量的研究显得尤为重要。本文利用Hilbert-Huang变换方法对2008年汶川8.0级强震进行分解,研究其输入能量,得到了地震动输入能在频域的分布特性。并对边际能量谱分析,发现地震动的频谱特性与傅立叶谱吻合。
1 基于希尔伯特–黄变换的汶川地震动分析
2 结论
本文运用HHT方法分析了2008年汶川8.0级地震6个台站的强震记录,通过EMD分解,分析了地震动IMF分量的强度及频谱特性,可得结论如下:
(1)利用EMD将地震波分解成不同数量的IMF分量,进而对地震波输入结构的总能量进行分解,得到地震动能量在IMF分量之间的分布关系。
(2)通过对各分量边际能量谱的分析,可以从另外一个方面得到地震的频谱特性,边际能量谱的峰值频率与其对应地震动谱的卓越频率相同,边际能量谱也可以作为一种估算震动卓越周期的方法。
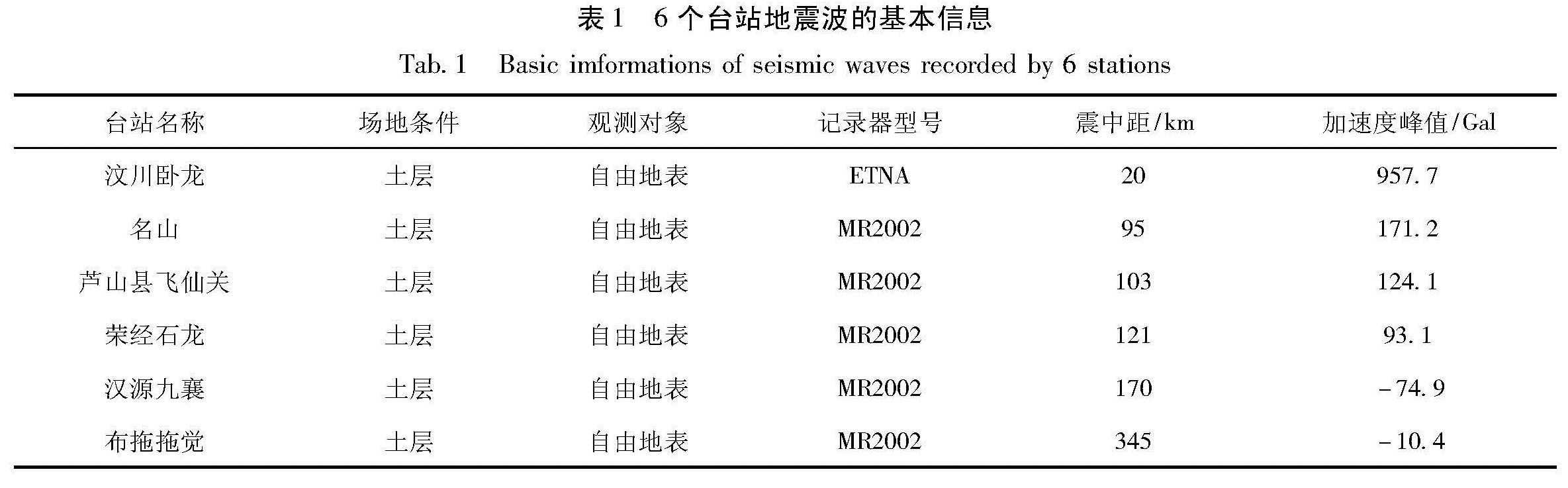
1.1 台站选取笔者选取汶川卧龙、名山、芦山县飞仙关、荣经石龙、汉源九襄和布拖拖觉6个台站所记录的汶川MS8.0地震东西向地震动加速度记录,每个台站原始地震记录采样间隔0.005 s,为方便准确地对各个台站地震动记录进行对比分析,对所有台站地震动采样间隔统一取0.05 s,采样起始时间统一到2008年5月12日14时28分21秒,采样长度为140 s。各个台站地震记录的基本信息如表1所示。
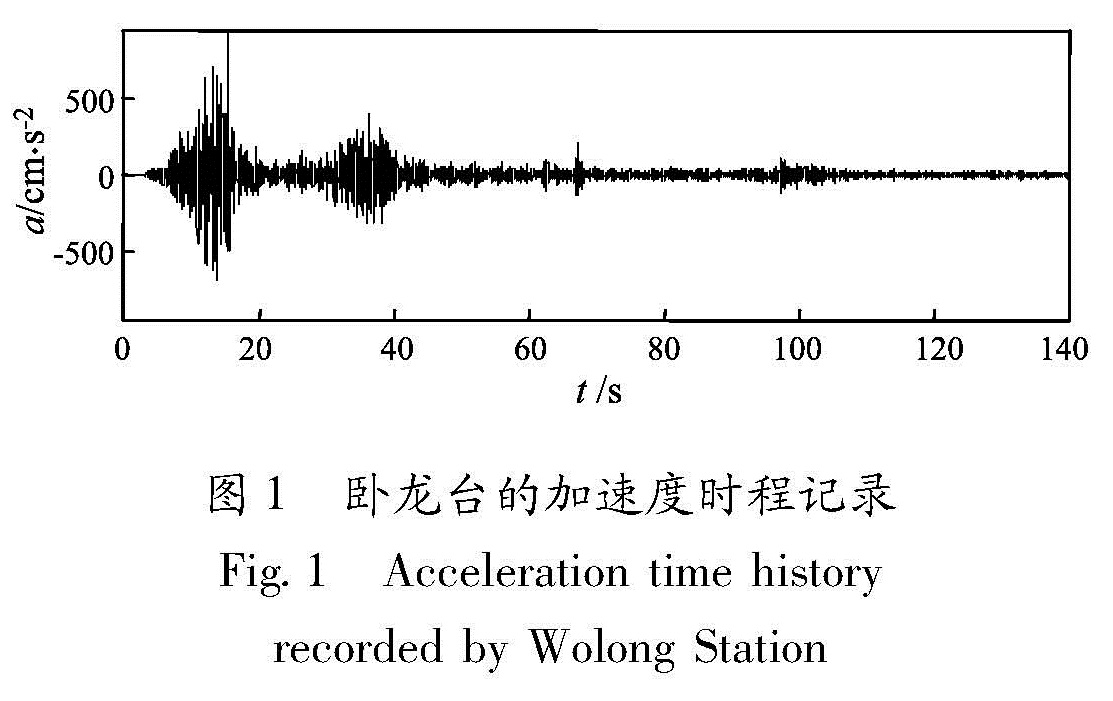
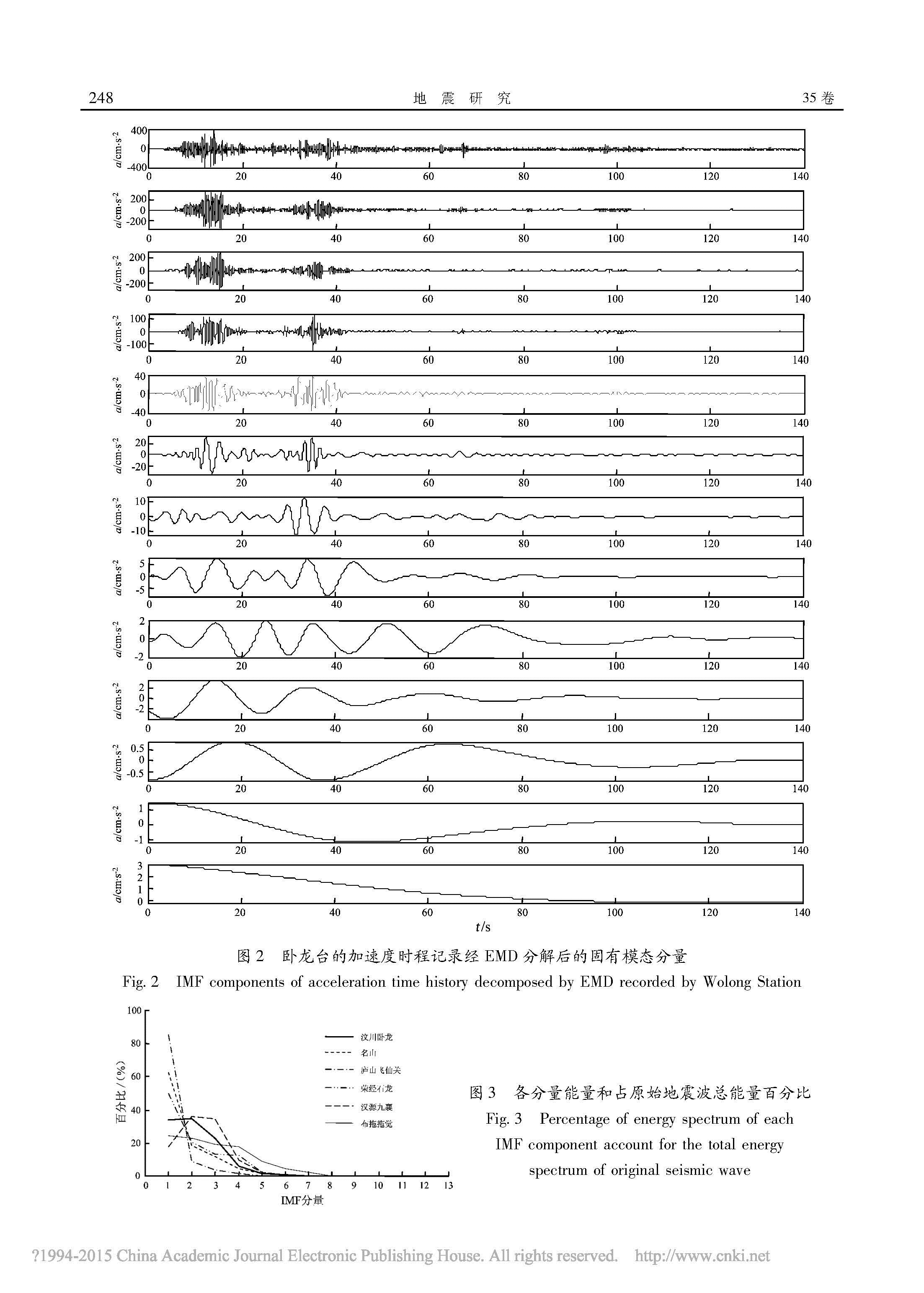
1.2 地震动的EMD分解笔者对6个台站的汶川地震加速度记录分别进行经验模态分解,得到不同数量的固有模态分量,下面仅列出汶川卧龙台的加速度时程记录(图1)及其经过经验模态分解后的固有模态分量(图2)。
1.3 地震动的Hilbert能量谱分析1.3.1 地震动的Hilbert边际能量谱强度分析对6个台站的地震记录及其固有模态分量分别求边际能量谱,然后对边际能量谱进行求和得到原始地震记录和各分量的总能量。根据能量守恒原理,原始地震记录的总能量与各分量能量的和应该相等,本文的计算结果也是如此。从表2中可以看出随着震中距的增大,地震动总能量快速衰减,震中距由汶川卧龙台站的20 km扩大到布拖拖觉台站的345 km时,能量由741×106 Gal2衰减到0.623×106 Gal2,能量衰减了大约99.92%。
图3表示每个台站地震波所分解出的IMF分量的能量占该站记录的地震波总能量的百分比,从图中可以看出地震动能量主要集中在前5个IMF分量,能量比重最大的通常在第1或者第2个IMF分量,到第6个IMF分量时6条地震波中的5条能量比重已经趋近于0。因此在利用希尔伯特—黄变换对地震动能量进行分析时,可以对前几个固有模态分量进行重点研究。
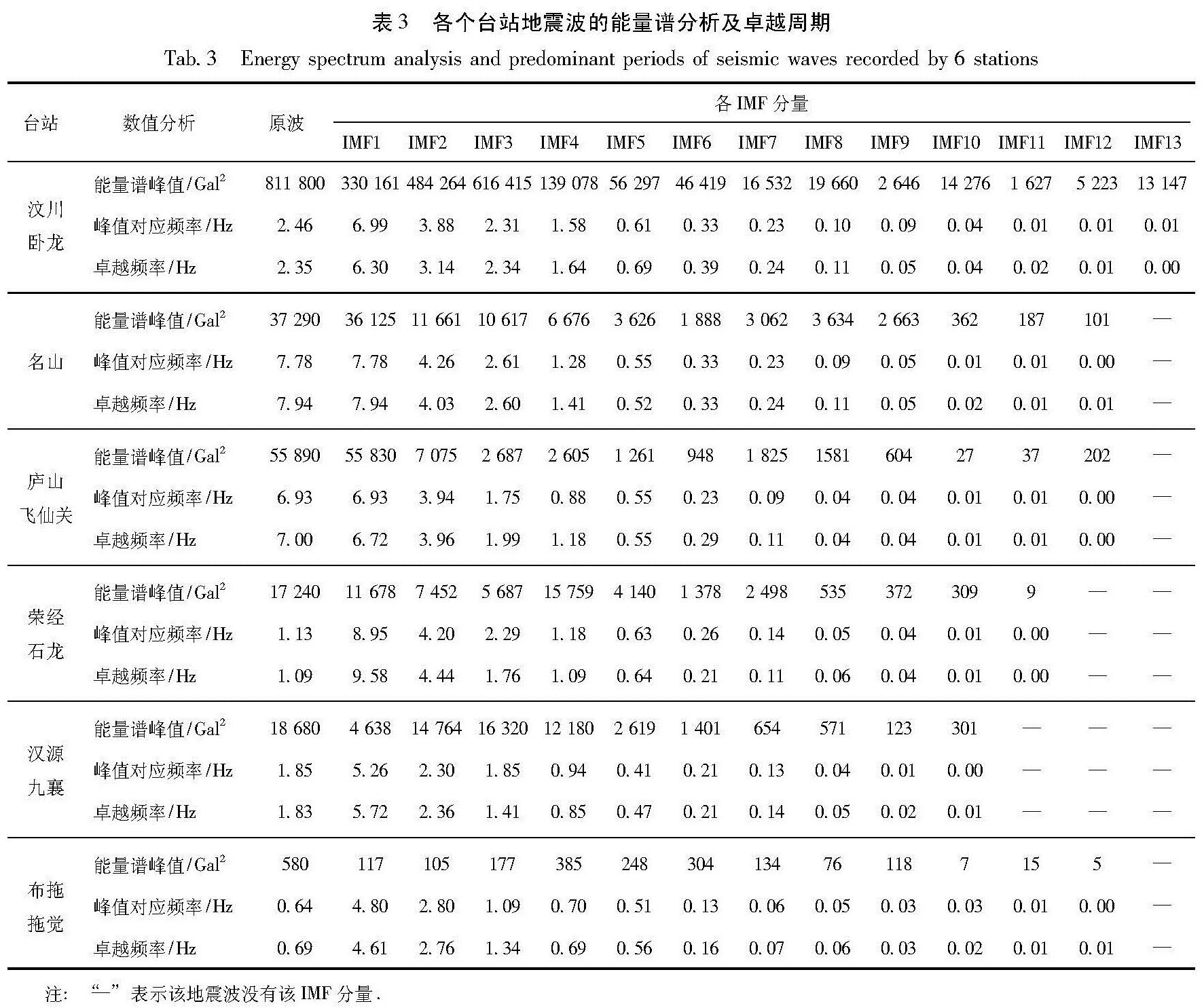
1.3.2 地震动的Hilbert边际能量谱频率分析表3中列出了对各个台站进行经验模态分解后,分别对原始地震波和IMF分量求取边际能量谱的谱峰值、边际能量谱峰值所在频率以及卓越频率(傅立叶谱峰值所在频率)。
注:“—”表示该地震波没有该IMF分量.图2 卧龙台的加速度时程记录经EMD分解后的固有模态分量
Fig.2 IMF components of acceleration time history decomposed by EMD recorded by Wolong Station图3 各分量能量和占原始地震波总能量百分比
Fig.3 Percentage of energy spectrum of eachIMF component account for the total energy spectrum of original seismic wave注:“—”表示该地震波没有该IMF分量.表3 各个台站地震波的能量谱分析及卓越周期
Tab.3 Energy spectrum analysis and predominant periods of seismic waves recorded by 6 stations从表3和图4中可以看出,各个台站的能量谱峰值并不像其能量一样集中在前两个IMF分量,而是相对分散地分布在第1到第4个IMF分量中,并且部分IMF分量能量谱峰值在原始地震波能量谱峰值中所占比例很大:汶川卧龙台记录地震波IMF3分量占75.93%; 名山台记录地震波IMF1分量占96.88%; 庐山飞仙关台记录地震波IMF1分量占99.89%; 荣经石龙台记录地震波IMF4分量占91.41%; 汉源九襄台记录地震波IMF3分量占87%; 布拖拖觉台记录地震波IMF4分量占66.32%,这说明在地震动对结构的影响上,这些分量是卓越的,我们将这种分量称为能量卓越分量。图4 各分量能量谱峰值占原始地震波能量谱峰值的百分比
Fig.4 Percentage of energy spectrum peak of each IMF component account for the total energy spectrum peak of original seismic wave抗震设计的重要目标之一就是使结构的自振频率远离结构输入地震能量集中的频段,因而使用地震动能量特征来评价地震波的特性(大小、持时、频率等)是一个很好的选择。
进一步对这些能量卓越分量进行分析,发现这些卓越分量能量谱峰值所在的频率和原始地震波的傅立叶谱卓越频率非常一致,由此可以用边际能量谱峰值所在的频率来表示原地震波的卓越频率。
- 公茂盛,鹿嶋俊英,谢礼立,等.2010.基于结构强震记录的结构时变模态参数识别[J].振动与冲击,29(5):171-176.
- 公茂盛,谢礼立,连海宁,等.2007.基于HHT的结构强震记录分析研究[J].地震工程与工程振动,27(6):24-29.
- 鞠萍华,秦树人,秦毅,等.2009.多分辨EMD方法与频域平均在齿轮早期故障诊断中的研究[J].振动与冲击,28(5):97-103.
- 祁克玉,施坤林,霍鹏飞,等.2010.EMD端点效应处理在转子摩擦故障诊断中的应用[J].振动、测试与诊断,30(5):492-496.
- 王彬,杨润海,郭梦秋,等.2005.昆明高层建筑强震观测记录HHT分析[J].地震研究,28(1):78-81.
- 周挚,山秀明,梁虹,等.2005.固体潮时频分析新方法[J].地震研究,28(4):334-339.
- Duffy D G.2004.The application of Hilbert-Huang transforms to meteorological datasets[J].Oceanic Technol,21(4):599–611.
- Huang N E,Shen Z,Long S R,et al.1998.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary Time Series Analysis[C].Proc R Soc Lond A,454(1971):903-995.
- Huang N E,Zheng S,Steven R L.1999.A new view of nonlinear water waves:The Hilbert spectrum[J].Annu Rev Fliud Mech,31:417-457.
- Jia R Y,Shou Z F,Shieh J S.2009.Human heart beat analysis using a modified algorithm of detrended fluctuation analysis based on empirical mode decomposition[J].Medical Engineering & Physics,31(3):92–100.
- Jiang R,Yan H.2008.Studies of spectral properties of short genes using the wavelet subspace Hilbert-Huang transform(WSHHT)[J].Physica A,387(16):4 223-4 247.
- Li M,Jiang W M,Li X,et al.2005.A test of the dynamical nonstationarity in atmospheric boundary layer turbulence [J].Chin J Geophys,48(3):493–500.
- Ortega J,Smith G H.2009.Hilbert-Huang transform analysis of storm waves[J].Applied Ocean Research,31(3):212-219.
- Zhang R R,Ma S,Stephen H.2003.Hilbert-Huang transform analysis of dynamic and earthquake motion recordings[J].Journal of engineering mechanics,129(8):861-875.