(1.甘肃省地震局 兰州观象台,甘肃 兰州 730046; 2.甘肃省地震局,甘肃 兰州 730000; 3.甘肃省地震局 高台地震台,甘肃 高台 734300)
(1.Lanzhou Observatory Station,Earthquake Administration of Gansu Province,Lanzhou 730046,Gansu,China)(2.Earthquake Administration of Gansu Province,Lanzhou 730000,Gansu,China)(3.Gaotai Seismic Station,Earthquake Administration of Gansu Province,Gaotai 734300,Gansu,China)
64-type seismometer; simulation; transfer function; zero-pole values; Lanzhou Observatory Station
备注
依据地震仪仿真的原理和方法,通过整理兰州台64型地震仪多年的模拟记录标定数据,由已知64型地震仪的传递函数表达式,通过分析计算,求解得到零极点值。把64型地震仪作为目标仿真仪添加到分析软件中,并在兰州台日常的大震速报和分析工作中得以检验。结果 表明64型地震仪对中远距离弱震、较小的极远震以及发生在兰州台影区的地震进行仿真,可以清晰的识别初至P波到时、初动方向与提高震相辨别。
Based on the principle and method of seismometer simulation,we made the EDSP-IAS analysis software as a platform in daily work and processed the calibration data of analog recording for many years.Using the known transfer function of 64-type seismometer,we obtained the zero-pole value by means of analyzing calculation.We made the 64-type seismometer as a target simulation instrument added to the EDSP-IAS analysis software,and the improved software had been verified in the large earthquake rapid alerting and analysis work in Lanzhou Station.The results showed that we simulated the weak earthquake in medium-long distance,smaller ultra-distant earthquake and the earthquake occurred in the shade area in Lanzhou Station by 64-type seismometer,we can easily discriminate the arrival time of initial P-wave,first motion direction,and the phase discrimination has greatly improved by 64-type seismometer.
引言
随着科学技术的不断发展,地震观测技术已由数字地震仪系统逐步取代了模拟记录系统。在数字地震观测时代,地震仪仿真是连接模拟和数字观测的纽带。为了保持历史记录和震级测定的一致性,延续模拟仪器记录震相的特征,人们希望通过地震仪仿真产生近似真实的传统模拟地震仪记录,从而根据传统的地震波形分析方法识别解释震相。因此,在日常的震相分析中,地震仪仿真已成为数字地震记录分析中不可缺少的工具①。要做好震相分析和大震速报工作,既要掌握震相识别的原则和方法,又要进行综合分析。根据不同类型地震的震相特征,充分利用数字地震记录动态范围大、频带范围宽、记录精度高、能记录到更多的信息等优势,进行震相综合分析(彼得·鲍曼,2006)。对要分析查找的震相,根据其特点,在最佳的记录上判读,也就是说要在仿真为最理想的仪器记录上读取,这样才能真正发挥数字地震记录的特点和优势,做到大震速报既迅速又准确,地震观测报告震相内容既正确又丰富(陈翔等,2011)
中国地震局“九五”数字地震台网建设之前,我国的地震观测主要是用模拟地震仪进行记录的。数字化地震仪具有大动态、宽频带、高精度及便于计算机处理等优点,是地震观测技术的一大进步(唐明帅,2003)。但由于数字地震记录波形与位移型模拟记录形态的差异,分析人员尚不习惯利用原始的数字记录进行震相分析和震级计算(孟晓春,2007)。
兰州台已于2001年完成“九五”数字化改造,64型模拟地震仪一直和数字宽频带地震计CTS-1并行观测。目前,国家数字地震台和区域有人值守数字地震台所用的日常分析软件EDSP-IAS和MSDP均具有数字仿真的功能,但其中只给出了几种典型地震仪的仿真。由于模拟观测时期64型短周期地震仪布设少,相关的研究也很少,推广软件也不适用于64型模拟地震仪。兰州台长期使用64型地震仪进行模拟记录,分析人员十分熟悉其记录特征,后因图纸短缺等原因停记,给日常分析工作以及分析的精度带来较大的影响。由于台基和观测环境所限,兰州台记录到的一些较小地震、距离较远的中强地震以及发生在影区的地震的初至P波初动很弱。P波到达时,记录波形中会产生幅值和频率的变化,所以用于识别P波震相的特征参量必须能反映这些变化趋势,才能较为准确地识别P波震相(毛燕等,2011)。而兰州台数字化宽频带地震计CTS-1记录不论是速度记录还是被仿真为短周期DD-1型的记录,其对一些地震记录的P波初动不是很清晰,不易识别,很难找到准确的初至波震相到时,而64型地震仪模拟记录图上则能够清晰地分辨。为了能够充分利用已停用的64型地震仪,本文通过整理兰州台多年来64型地震仪的一些标定参数,经过分析计算和可行性研究,把64型地震仪作为目标仿真仪,添加在目前使用的地震分析软件中,以提高震相识别和大震速报能力,为兰州台的资料处理提供一种新途径。
1 仿真原理及实现
2 实例分析
笔者主要选取兰州台记录范围内影区的地震,距离较远的弱震以及较小的极远震来进行DD-1型和64型地震仪仿真结果对比分析。所选取的地震
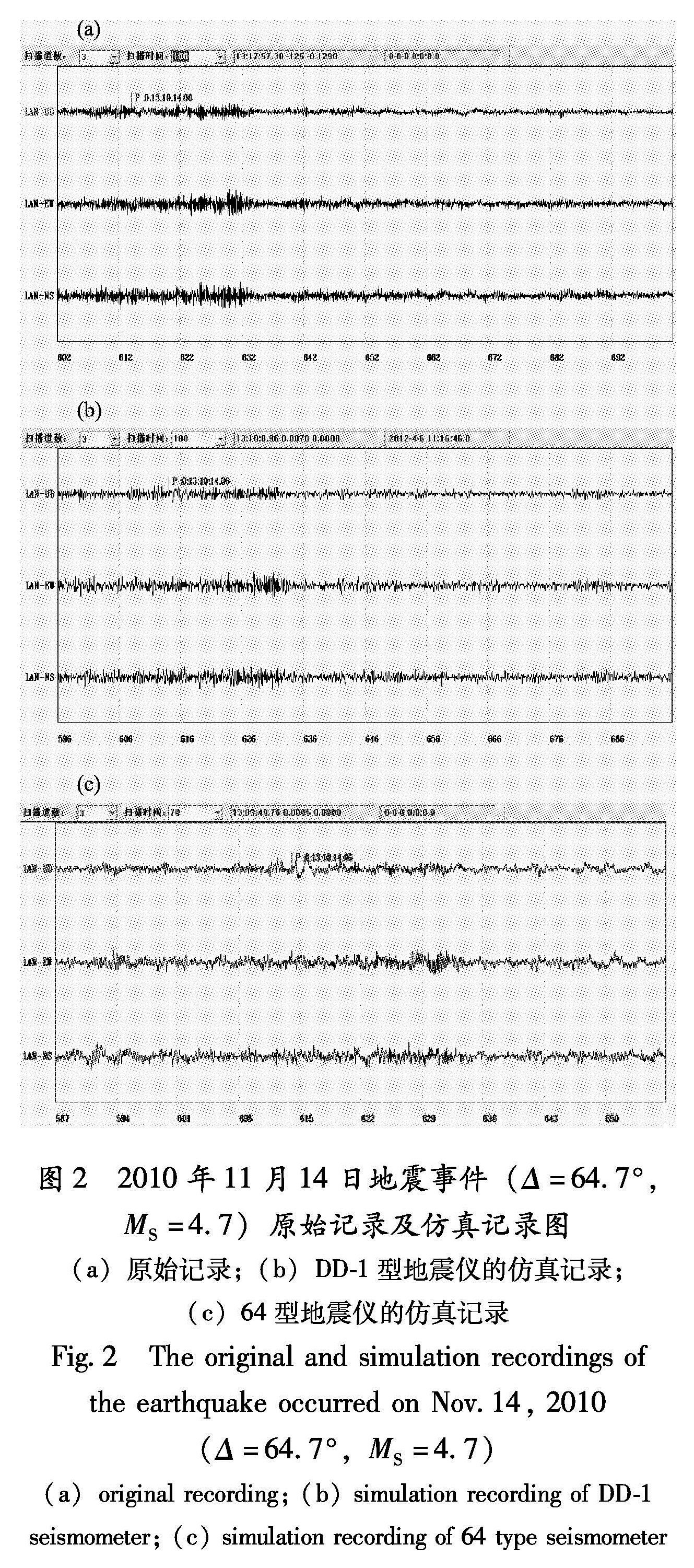
事件来自中国地震台网中心。对同一地震原始速度记录分别用短周期的DD-1型和64型地震仪进行仿真对比分析。图2 2010年11月14日地震事件(Δ=64.7°,
MS=4.7)原始记录及仿真记录图
(a)原始记录;(b)DD-1型地震仪的仿真记录;
(c)64型地震仪的仿真记录
Fig.2 The original and simulation recordings of the earthquake occurred on Nov.14, 2010(Δ=64.7°,MS=4.7)(a)original recording;(b)simulation recording of DD-1 seismometer;(c)simulation recording of 64 type seismometer如图2所示是原始波形记录图和经过更新的EDSP-IAS分析软件用短周期DD-1和64型仪的仿真一段数字记录,由于该地震震级小,震中矩远,所以初至波震相很不明显,短周期的DD-1型地震仪仿真地震记录难以辨认,完全找不到初至P波到时。而使用64型地震仪仿真后,在13:10:14.06
能很清晰的辨别到远震初至P波震相。
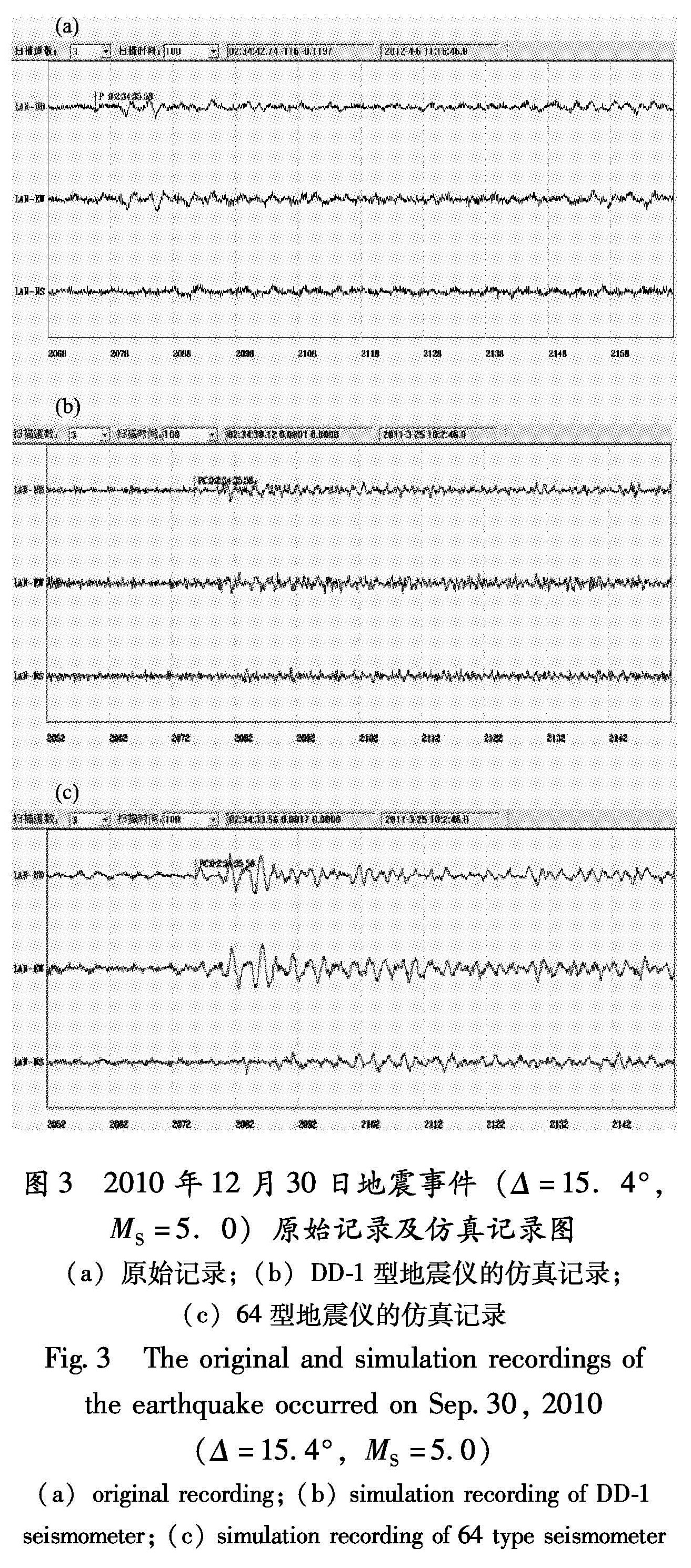
如图3所示是发生在兰州台影区范围内的地震,虽然距离不远,但初动很不明显,对初至P波到时辨认难度很大,用DD-1型地震仪仿真后,P波初动位置模糊不清,而用64型地震仪仿真之后,初动方向清晰向上,初至P波也清晰可见。
图4所示是一个极远震图例,用DD-1型地震仪仿真,初至PKP波到时很模糊,几乎找不到初至波,很难准确判断,而用64型地震仪仿真之后,
图3 2010年12月30日地震事件(Δ=15.4°,
MS=5.0)原始记录及仿真记录图
(a)原始记录;(b)DD-1型地震仪的仿真记录;
(c)64型地震仪的仿真记录
Fig.3 The original and simulation recordings of the earthquake occurred on Sep.30, 2010(Δ=15.4°,MS=5.0)(a)original recording;(b)simulation recording of DD-1 seismometer;(c)simulation recording of 64 type seismometer初至PKP波清晰可见。图4 2010年04月17日地震事件(Δ=177.6°,
MS=5.5)原始记录及仿真记录图
(a)原始记录;(b)DD-1型地震仪的仿真记录;
(c)64型地震仪的仿真记录
Fig.4 The original and simulation recordings of the earthquake occurred on Apr.17, 2010(Δ=177.6°,MS=5.5)(a)original recording;(b)simulation recording of DD-1 seismometer;(c)simulation recording of 64 type seismometer3 结论和讨论
(1)本文利用EDSP-IAS分析软件作为平台,根据多年原始标定数据为基础,通过计算求解得到了64型地震仪传递函数的确切零极点值,添加了64型地震仪为目标仿真地震仪这一功能,完善了兰州台测震分析软件EDSP-IAS仿真仪器系统。
(2)研究结果已应用到兰州台日常的分析和大震速报工作中,并取得了显著的效果,提高观测资料的精度和准度,文中列举的仅是一些典型震例。64型地震仪对得到中远距离弱震、较小的极远震以及发生在影区的地震的初至波到时、初动方向和震相辨别都有很大的帮助。
(3)从同一地震不同的短周期地震仪仿真效果来看,64型地震仪是电流计光记录仪,其的系统传递函数可被精确地描述出来,因而能更准确地反应系统的响应特性,而DD-1型地震仪属于电子放大式地震仪,其中电子部分的传递函数只是根据实测数据拟合而得,不准确且不唯一,因而影响了仿真结果,所以二者仿真结果差异比较明显。
(4)震相识别是一项十分复杂且经验性较强的工作,加之应用64型地震仪进行仿真这项工作开展不久,还有待在日常实际工作中长期对比检查。该做法在兰州台效果明显,初至波震相到时的识别辨别能力有了一定的提高,能否应用于别的测震台站,还需要做进一步的实际检验,各台站应利用多种数据处理分析方法进一步提高震相的识别能力和到时准确性。
1.1 仿真原理和方法地震仪仿真就是将给定的地震波记录通过适当处理,如滤波、褶积、微分、积分等,仿真成另一种类型的波形记录,使两者在相位和幅度上保持一致(魏斌,2003)。进行地震仪仿真前,需要知道原始记录地震仪的特性和仿真的目标地震仪的特性。在作仿真处理时,要求原始记录系统频带宽具有稳定明确的传递函数,被仿真的地震仪系统传递函数也应明确稳定(何少林,1997)。本文选用兰州台运行多年的数字化宽频带地震计CTS-1记录仪作为原始记录仪,选用短周期DD-1型和64型地震记录仪作为被仿真的地震仪系统。
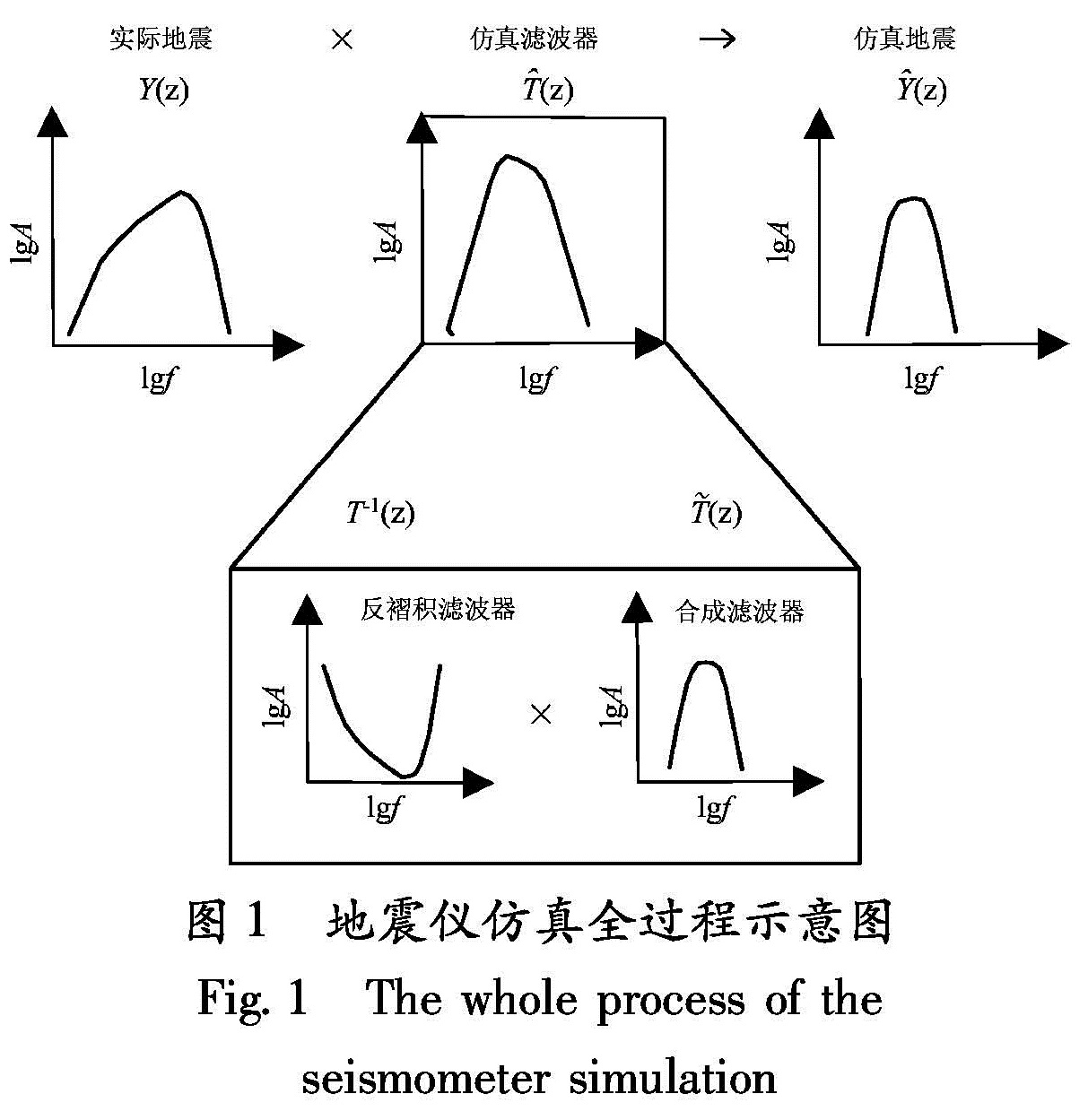
如图1所示,不同地震仪系统的数字仿真过程。仿真滤波器可被认为是实际记录系统的反滤波器和仿真记录系统的合成滤波器的组合。图中显示有贡献的各子系统的振幅频率响应函数 赵仲和.2009.地震仪仿真有数字波形分析中的应用.。地震记录仿真常使用傅立叶分析法:设U(s)是地面运动的频
谱、Y(s)是数字地震记录的频谱、G(s)是数字地震仪的传递函数,则有Y(s)=U(s)·G(s)。设模拟记录的频谱为X(s), 模拟地震仪的传递函数为T(s), 则有X(s)=U(s)·T(s)=Y(s)·T(s)/G(s)。
1.2 64型地震仪仿真的实现当地震发生时,地震仪记录了地震信号,而我们从计算机中读出的信号只是一些无量纲整数,并非是真正的地动速度和地动位移,它必须和数字地震仪系统的传递函数进行反褶积才能得到地动速度,然后进行积分得到地动位移,因此,获得数字地震仪系统的传递函数是至关重要的(付虹等,2009; 颜其中,2003)。目前,获得整个地震仪系统传递函数的方法是分别计算地震计、数据采集器(或电流计、记录器)等各组成部分的传递函数,然后在变换域相乘,计算地震计的传递函数是直接求解简化了的摆的动力学微分方程,而数据采集器(包括放大器、滤波器、模数转换等)都是理论设计分析得到的传递函数,各部分传递函数通常用零点、极点给出(陈运泰等,2000; Bormann,2002)。64型地震仪是电流计放大光记录仪,其运动方程比较明确,因而可以得到比较精确的传递函数,王广福(1983)已推导出64型地震仪准确的传递函数表达式。
1.2.1 运动方程和传递函数64型地震仪的运动方程式如下:
{θ ··+2n1D1θ ·+n21θ=-(χ··)/l+k(K2)/(K1)y·,
y ··+2n2D2y·+n22y=2Agkθ ·.(1)
或写作: y····+my···+py··+qy·+sy=-(2Agk)/lχ···.(2)
式中, m=2(n1D1+n2D2); p=n21+n22+4n1D1n2D2(1-σ2); q=2(n1D1n22+n21n2D2); s=n21n22; n1=2π1/(T1); n2=2π1/(T2)k=((K1)/(K2)4n1D1n2D2σ2)1/2.
其中θ是摆的转角; y是记录图上的光点偏移; l是折合摆长; Ag是示波器光杠杆长度; n、D和K分别表示摆和电流计的固有圆频率、阻尼常数和转动惯量,以下标“1”和“2”区别; σ2为耦合系数。
电流计放大光记录地震仪的传递函数如下:
KW(S)=V0W(S)
=-(2Agk)/l(S3)/(S+mS3+pS2+qS+S),(3)
在“正耦合”情况 (D1T2)/(D2T1)<1时,
V0D=(2Ag)/l((K1)/(K2)(D1T2)/(D2T1)σ2)1/2,(4)
WD(S)=(2n2D2S3)/(S4+mS3+pS2+qS+S).(5)
1.2.2 零极点值的计算兰州台64型地震仪工作基本常数:T1=2.5,T2=0.1,D1=0.5,D2=6.0,σ2=0.3分别代入(3)式求解的值分别是:n1=2.51,n2=62.83,m=756.49,p=5280.63,q=14684.57,S=24936.73,A=753.98。
根据零极点值的定义,零点是分子的根:当S3=0时,得到3个值为0的根,即Z1=Z2=Z3=0,极点是分母表达式的根,即:
S4+mS3+pS2+qS+S=0 .(7)
把已求得到m,p,q,s的数值代入(7)式,求得64型地震仪的零极值点有4个,分别是:(-748.75,0.0),(-5.22,0.0),(-1.26,2.19),(-1.26,-2.19).
1.2.3 分析软件的更新改进根据EDSP-IAS分析软件的固定格式,把已求得的零极值点添加到CFG文件夹中,保存并更新数据,将64型地震仪作为被仿真仪器选项添加到兰州台分析系统软件中得以实现。软件给定的固有格式更新完成如下:
PAZ
64 0 0
753.98 753.98 753.98 10.
3
0.0.
0.0.
0.0.
4
-748.75 0.0
-5.22 0.0
-1.26 2.19
-1.26 -2.19
- 彼得·鲍曼.2006.新地震学观测实践手册[M].中国地震局监测预报司译.北京:地震出版社.
- 陈翔,沈道康,夏丽红,等.2011.2009年汤加MS7.7地震的震相特征分析[J].地震研究,34(2):173-177.
- 陈运泰,吴忠良,王培德,等.2000.数字地震学[M].北京:地震出版社.
- 付虹,王绍晋,龙晓帆,等.2009.利用数字化速度波形和仿真位移波形资料求解震源机制的比较[J].地震研究,32(1):47-51.
- 何少林.1997.中国数字地震台网数字化地震数据的仿真处理[J].西北地震学报,19(3):11-17.
- 毛燕,崔建文,郑定昌,等.2011.地震记录的P波自动捡拾[J].地震研究,34(1):47-51.
- 孟晓春.2007.地震学与地震观测[M].北京:地震出版社.
- 唐明帅.2003.数字地震仪传递函数幅频特性及其应用的分析[J].高原地震,15(2):55-55.
- 王广福.1983.我国基准地震台上使用的十二种地震仪的传递函数、频率特性和时间特性[J].地震地磁观测与研究,17(3):8-10.
- 魏斌.2003.数字仿真技术在数字地震台的应用[J].内陆地震,17(3):277-278.
- 颜其中.2003.数字地震仪系统传递函数的一种计算方法[J].地震学报,25(6):667-671.
- Bormann P.2002.New manual of seismological observatory practice[M].Postdam:Geo Forschungs Zenteum.