数字地震观测技术的快速发展为提高地震台网信息处理能力和服务功能提供了先决条件(金星等,2007a; 曲均浩等,2010)。在数字地震台网的数据处理系统中,地震自动定位结果已成为一种常规产出(金星等,2007b),地震发生后能够快速准确、稳定可靠地测定地震三要素,是对地震速报提出的一项迫切要求。提高地震定位精度一直是地震学应用研究的重要课题之一,也是自动定位系统的技术难点之一,开展地震定位方法的研究对提高地震定位精度意义重大(赵仲和,2005)。

地震精确定位属于地球物理反演问题,该问题可归结为在离散的、有限的数学结构上,寻找一个满足给定约束条件并使其目标函数值达到最大或最小的解。一般来说,地球物理反演问题通常带有大量的局部极值点,往往是不可微的、不连续的、多微的、有约束条件的和高度非线性。因此,精确求解问题的全局最优解一般是不可能的,但可以通过不断提高台站观测密度和完善空间观测布局、最大程度地利用观测中的已知信息、尽可能减小人为观测误差、不断积累震例资料、不断修正和完善地壳速度模型、利用最优的非线性理论和方法得到最接近真实的解。因此,要始终把解决可能会导致地震定位误差的因素作为重点问题来考虑。归结起来,地震定位误差的来源有3项(蔡明军等,2004):一是直达 P波和 S波到时读取误差,二是模型误差,三是线性化误差(线性定位方法)或离散化误差(非线性定位方法)。

遗传算法(Genetic Algorithm,简称GA)是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,是一种能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程,从而得到最优解或准最优解的通用搜索算法,于20世纪80年代末和90年代初期兴起。

遗传算法用二进制数来表示问题的待求解,将二进制数串联在一起形成一个由0和1组成的字符串,其中把二进制数看作一个基因,把字符串看作一个染色体(个体),问题的解包含在一个字符串中(栾锡武,1997)。随机地生成包含有不同染色体的个体,由此生成一个种群。在种群的演化过程中,其中的个体根据目标函数的大小进行淘汰、保留。人为地保持种群的大小不变,保留下来的个体通过基因的遗传和变异而形成新的种群,如此反复,最终得到最优的种群。这个种群中字符串所代表的参数即为问题的解。最小化的遗传算法单个迭代过程要经过繁殖、交配和变异3个计算过程(周民都,张元生,1999)。

当地震事件触发时,每次获取的台站震相并非都是理想的数据,各个台站震相各异,参与定位的一组震相也并非都是相同的,因而必须对自动拾取的台站震相进行合理筛选。笔者主要考虑以下4种情况:(1)利用到时最早的第一个台站的2个震相和其余台站的Pg震相进行定位,要求记录的第一个台站有S波记录;(2)对到时最早的第一个台站记录的S波进行合理性检验和校正,要求到时最早的第二个台站识别到S波信息,利用到时最早的第一个台站两个震相和其余台站Pg震相进行定位;(3)对到时最早的第二个台站记录的S波进行合理性检验和校正,要求到时最早的第一个台站识别到S波信息,利用到时最早的第二个台站的两个震相和其余台站的Pg震相进行定位;(4)如果系统仅识别到Pg波到时,则单利用所有台站的Pg震相进行定位。当多种情况发生时,取其中残差最小的结果做为最终的定位结果。

假定系统自动识别的各台直达Pg震相是比较准确的,当Pg波到时最早的第一个台站记录的Sg-Pg大于第二个台站时,对第一个台站的Sg波到时T_S1进行校正

T_S1=P₁+(S₂-P₂)+((P₁-P₂))/a.(1)

当Pg波到时最早的第二个台站记录的Sg波与第一个台站的Sg波到时之差太大时(超过理论值1.2倍),对第二个台站的Sg波到时T_S2进行校正

T_S2=T_S1+((P₂-P₁)·(a+1))/a.(2)

在人机交互进行地震精定位过程中,首先利用所有震相数据参与定位,根据初始定位结果确定各台站震相走时差,然后排除走时差超过1倍的走时残差标准差的震相数据,再进行精定位。

平均残差计算公式为

η=∑^sta_i=1(|obs_i-cal_i|)/(sta×delta_i),(3)

标准残差计算公式为

σ=(∑^sta_i=1((|obs_i-cal_i|/delta_i-η)²)/(sta-1))^1/2.(4)

式中,obs_i为第i个台站的观测走时; cal_i为第i个台站的计算走时; sta为台站的总数; delta_i表示地震距离第i个台站的震中距。

地震精确定位解决的前提是得到所研究区域的三维速度结构,笔者根据前人对该区域地下速度结构的研究,汇总了4种速度结构(表1),建立了山东地区三维速度模型。具体思路如下:以(36.0°N,118.0°E)为坐标原点,坐标系由北—东—垂直(下)组成,在东西方向上分别垂直于南北方向,以交点距离坐标原点长度为-1 000.0,-600.0,-500.0,-400.0,-300.0,-200.0,-100.0,0.0,100.0,200.0,300.0,400.0,500.0,600.0和1 000.0 km的位置作为块体的边界; 在南北方向上分别垂直于东西方向,以交点距离坐标原点长度为-1 000.0,-600.0,-500.0,-400.0,-300.0,-200.0,-100.0,0.0,100.0,200.0,300.0,400.0,500.0,600.0和1 000.0 km的位置作为块体的边界。这样就把以(36.0°N,118.0°E)为中心,将包括山东地区在内的区域为(2 000×2 000)km²范围内的地壳划分为每层256个块体。在垂直方向上,根据地

表1 地壳层状均匀速度模型
Tab.1 Crustal homogeneously layered velocity model

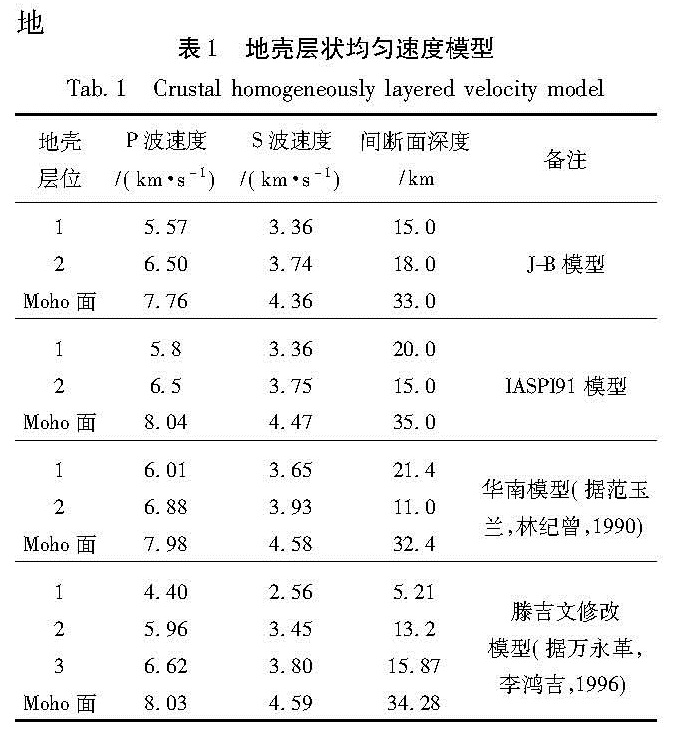
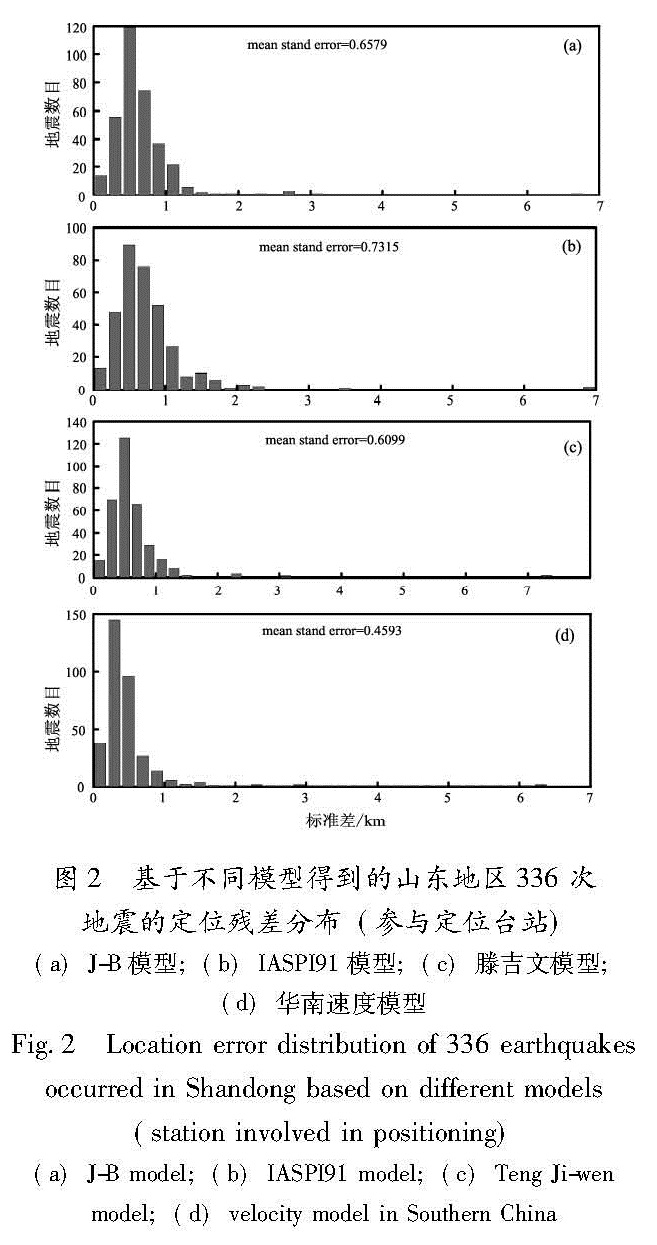
选择山东地区2009年发生的336次地震的台站观测报告中Pg和Sg到时资料,分别选择不同的速度模型,应用遗传算法进行地震定位。按照间隔0.2统计分布频次,定位结果的残差分析分两种情况:第一种是统计所有台站的走时残差分布(图1),应用J-B模型、IASPI91模型、滕吉文修改模型和华南模型所得到的平均定位标准残差分别是0.89、0.95、0.81和0.64; 第二种是只统计参与定位台站的走时残差分布情况(图2),应用J-B模型、IASPI91模型、滕吉文修改模型、华南模型所得到的平均定位标准残差分别是0.66、0.73、0.61和0.46,以上结果都说明华南速度模型与山东地区真实的速度模型更为接近。

高星等(2005)通过对中国及邻近地区地壳结构的研究表明,华北、华东和华南地区地壳厚度变化平缓,绝大部分地区为30～35 km。蔡学林等(2007)认为,中国大陆的地壳结构类型分为克拉通型地壳、增厚型地壳和减薄型地壳,华南地块和华北地块同属减薄型地壳,而且华南地块和华北地块上、中、下地壳三层的平均厚度和速度比较接近。本研究中所采用的模型对比中,利用华南速度模型的定位误差最小,具有合理性。

单纯型法是寻优算法的一种,该方法是在n维空间中,用(n+1)个顶点构成一个多面体。依据单纯型运算规则,计算各顶点的函数值,然后进行比较,确定顶点的优劣; 再次计算新点,用好的顶点代替差的顶点,这样不断地改变顶点,使单纯型朝着目标函数最小方向移动,最终获得准确解。

目前山东省数字地震台网使用由广东省地震局研发的JOPENS系统进行地震速报,其中包含有单纯型搜索方法、HYPO2000、Hyposat等定位方法,初步研究表明,单纯型搜索方法是区域地震定位精度较高的方法(石玉燕等,2008; 陈贵美等,2009)。

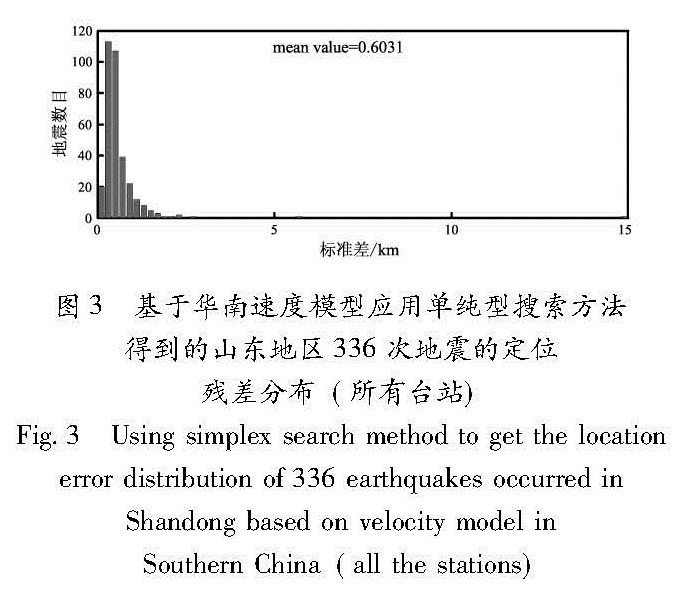
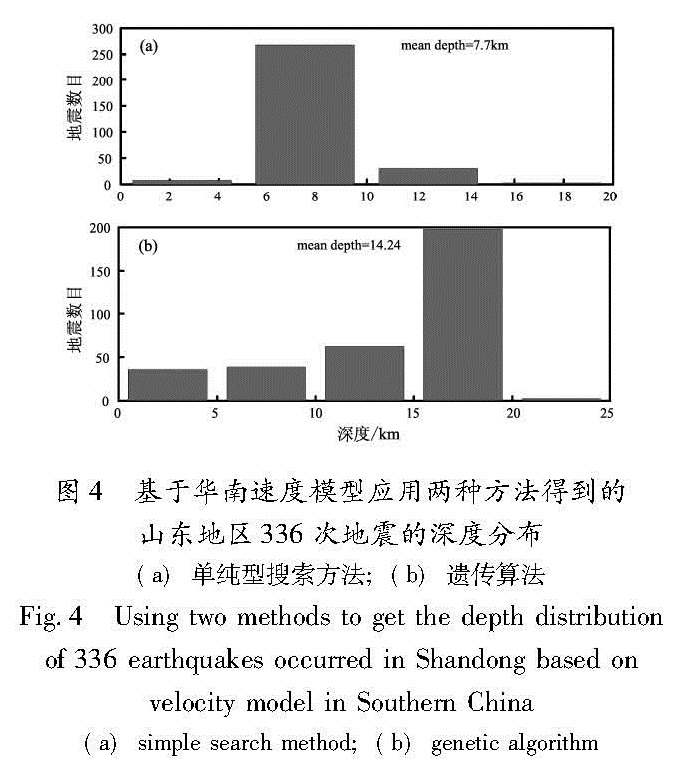
图3给出了由JOPENS系统中单纯型搜索方法所得到的山东地区336次地震的定位标准残差分布。336次地震标准差的平均值为0.60。由图1,2与图3分别进行比较可知,本项目开发的遗传算法与单纯型搜索方法的地震定位效果相当。应用上述两种方法所确定的地震定位深度有较大差异(图4),由单纯型搜索方法得到的震源深度集中于5～10 km范围内,平均深度7.7 km(图4a),而由遗传算法得到的震源深度范围较大,平均深度14.2 km(图4b)。

图3 基于华南速度模型应用单纯型搜索方法得到的山东地区336次地震的定位残差分布(所有台站)
Fig.3 Using simplex search method to get the location error distribution of 336 earthquakes occurred in Shandong based on velocity model in Southern China(all the stations)

图4 基于华南速度模型应用两种方法得到的
山东地区336次地震的深度分布
(a)单纯型搜索方法;(b)遗传算法
Fig.4 Using two methods to get the depth distribution of 336 earthquakes occurred in Shandong based on velocity model in Southern China(a)simple search method;(b)genetic algorithm

(1)本文提出了遗传算法中目标函数、适应度函数和变异概率选择的技术改进思路,还提出了地震自动定位中所使用震相的原则、震相筛选方法。

(2)选择遗传算法和4种速度模型分别进行了地震定位,结果表明华南速度模型更适于描述山东地区地壳速度结构。

(3)利用华南速度模型,选择遗传算法和单纯型搜索方法分别进行地震定位,结果表明两种方法的震中定位精度相当,但地震定位深度有较大差异,由单纯型搜索方法得到的震源深度集中于5～10 km范围内,平均深度7.7 km,而由遗传算法得到的震源深度范围较大,平均深度14.2 km。

(4)由于本文定位方法使用S波震相较少,因此在地震自动定位系统中有应用前景。另外,本文的研究仅表明和J-B速度模型、IASPI91速度模型和有关专家对华北地区的速度模型结果相比,华南地区的速度模型更接近山东地区真实的速度模型,要真正得到山东地区的速度结构还需结合本地的地震观测报告和波形记录进行详细研究。