基金项目:星火计划项目“青藏块体东北缘前兆系统结构分析与异常识别”(XH12072)资助.
(The Second Monitoring and Application Center,CEA,Xi'an 710054,Shannxi,China)
least square collocation; fixed point deformation; fitting; extrapolation
备注
基金项目:星火计划项目“青藏块体东北缘前兆系统结构分析与异常识别”(XH12072)资助.
将最小二乘配置方法的高斯型经验协方差函数模型应用于定点形变特征曲线的异常辅助识别,通过两个不同算例说明最小二乘配置滤波、内插和外推可以进行定点形变曲线的趋势模拟和辅助查找其短期、中长期的异常特征,对于定点形变曲线异常识别有一定的意义。
The Gauss-Function covariance model based on least square collocation was applied in the anomaly assisted identification of fixed point deformation characteristic curves. We used two different examples to show that the filtering,interpolation and extrapolation of least square collocation can be simulated the trend of fixed point deformation curves and assisted searching their anomaly characteristics in short-,medium-and long-term. The least square collocation method has certain significance for identifying the fixed point deformation.
引言
最小二乘配置是根据已知点信号、协方差及其与待估算点的协方差关系而获得的待估算点的无偏最优估计,它综合了平差、推估和滤波。张希等(1998,1999a,b),江在森和张希(2000)对该方法进行过深入的研究和探讨,将协方差经验函数进行了简化,并且将一维时间域内的推估内插进行了验证,武艳强等(2007,2004),马超和单新建(2005)将其用于GPS连续站资料分析,验证了反映时序变化特征的可行性。
本文选取“十五”数字化台站中两个定点测项,分别为四川姑咱钻孔应变和云南永胜垂直摆倾斜,时间范围为2008年1月1日至2011年12月31日(4年共1 461个日均值)。定点测项日均值很多(3年以上至少数千),如果都作为已知观测值,求逆矩阵相当费时,因此通过间隔一定天数取均值(本文均取5天)来进行计算。并将张希和江在森(1999b)的水平面最小二乘配置拟合模型应用于时间域内插,并进一步增加外推,应用到定点形变观测特征曲线寻找及其异常识别。
1 最小二乘配置方法原理
张希和江在森(1999b),武艳强等(2007),陶本藻等(1996),孔祥元等(2001)都对最小二乘配置方法的原理进行过相关的探讨和论证,对所选取高斯型经验协方差函数模型选择简单进行叙述。假设待内插区域有m0个已知点观测(或计算)值,设为L=(g1,g2,…,gm0)T,其中每个点值gi的中误差值为mgi(i=1,2,…,m0)。t为要滤波的已知点信号,n为观测误差向量,s是待估算点信号,t和n都是中心分布的。那么最小二乘配置的基本方程为
L=t+n.(1)
则
{t^=Ctt(Ctt+Cnn)-1L,
s^=Cst(Ctt+Cnn)-1L.(2)
其中,Ctt为已知点信号t的先验自协方差矩阵; Cnn为观测误差向量的自协方差矩阵; Cst为待估算点信号与已测点信号t之间的协方差。经推算的t^,s^的协方差分别为
{Ct^t^=Ctt-Ctt(Ctt+Cnn)-1Ctt,
Cs^s^=Css-Cst(Ctt+Cnn)-1Cts.(3)
将某一坐标为(x,y)的待估算点的值表示为g,用c(a,b)表示变量a,b间协方差,则
g=(c(g,g1),c(g,g2),…,c(g,gm0))(Ctt+Cnn)-1L.(4)
上述各式中,Cst,Ctt均由高斯型经验协方差函数f(d)=f(0)e-k2d2确定。其中,d为两点间距离,k为待定参数(张希等,1998,1999b; 江在森,张希,2000)。
假设Cnn为对角元素相等的对角阵,此对角元记为fr(0)=1/(m0)∑m0j=1mg2j,而fL(0)=1/(m0)∑m0j=1g2j,则f(0)=fL(0)-fr(0)。为保证f(0)>0,定义fr(0)=αfL(0)(0<α≤0.2),令α>0表示为必须滤波。
确定参数是最小二乘配置实现的关键,但一般情况下很难得到可靠性较好的协方差图形,故根据具体地区测点分布情况来确定参数k,即首先确定拟合量在整个区域的相关距离S(即超出这一距离,则点间协方差值接近于零)(张希,江在森,1999b),则参数
k=mink'{e-k'2、S2≤10-3}.(5)
设dij(i,j=1,2,…,m0)为任意两点间距离,则dmin=mini{minjdij}、d^-=1/(m0)∑m0i=1{minjdij}、dmax=maxj{minjdij}、Dmax=maxi{maxjdij}分别定义为最小相邻点距、平均相邻点距、最大相邻点距、最大点距。相关距离S可取为
S∈(max{1.2dmax,4d^-,0.2Dmax},max{1.5dmax, 4d^-,0.25Dmax}),且S≤0.5Dmax.(6)
事实上,相关距离S越大,得到的拟合场会比较平缓,某些局部剧烈变化可能被平滑掉; 而太小则不够光滑,且对整个区域整体变化趋势的反映不够。k值可人为设定,2年为2,4年即为4; 也可以范围确定后,根据式(5)~(6),程序自动计算缺省值,本文两个算例中k缺省计算值均为0.896(张希等,1998,1999b)。
2 定点形变曲线与异常识别应用实例
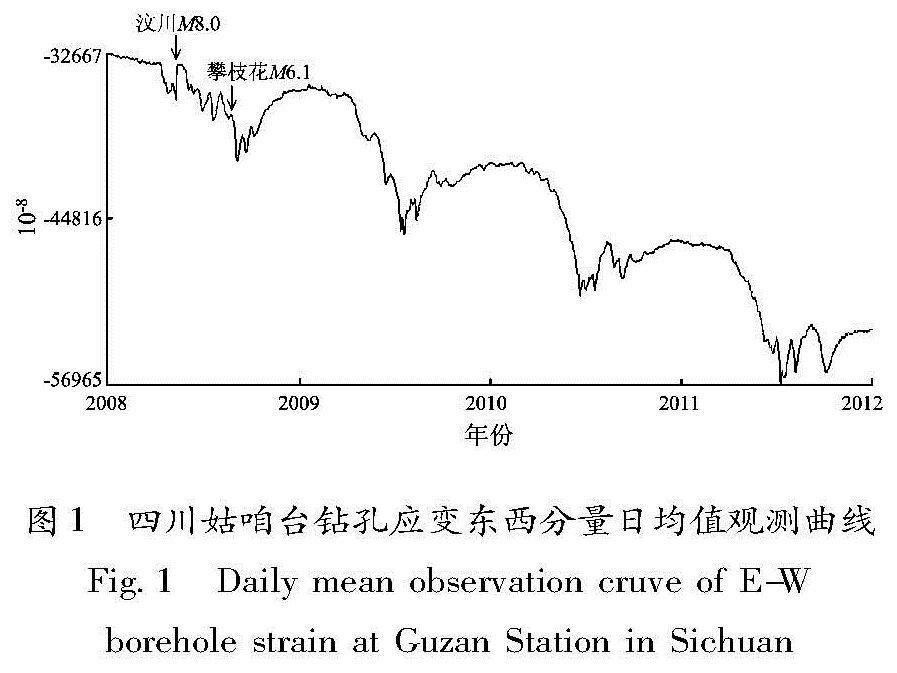
2.1 参数的选取和确定选取四川姑咱台“十五”数字前兆观测曲线(图1)作为算例一。四川姑咱台钻孔应变东西分量总体显示准周期性波动特征,在2008年5月12日汶川M8.0地震前该测项产生了持续的压性变化,震时至2008年8月下旬在下降趋势中呈现显著跳变,可能与攀枝花M6.1地震有一定关系,期间有人为停电的干扰,但总体呈现大震后非稳定状态,8月底至9月呈现波动上升; 2009年7~9月、2010年7~8月、2011年7~8月出现相似的波动上升,观测日志未说明原因、也无气象数据,可能反映了季节因素。计算整个观测时段相关范围分别为缺省值、2和4的特征曲线,所得结果见图2。
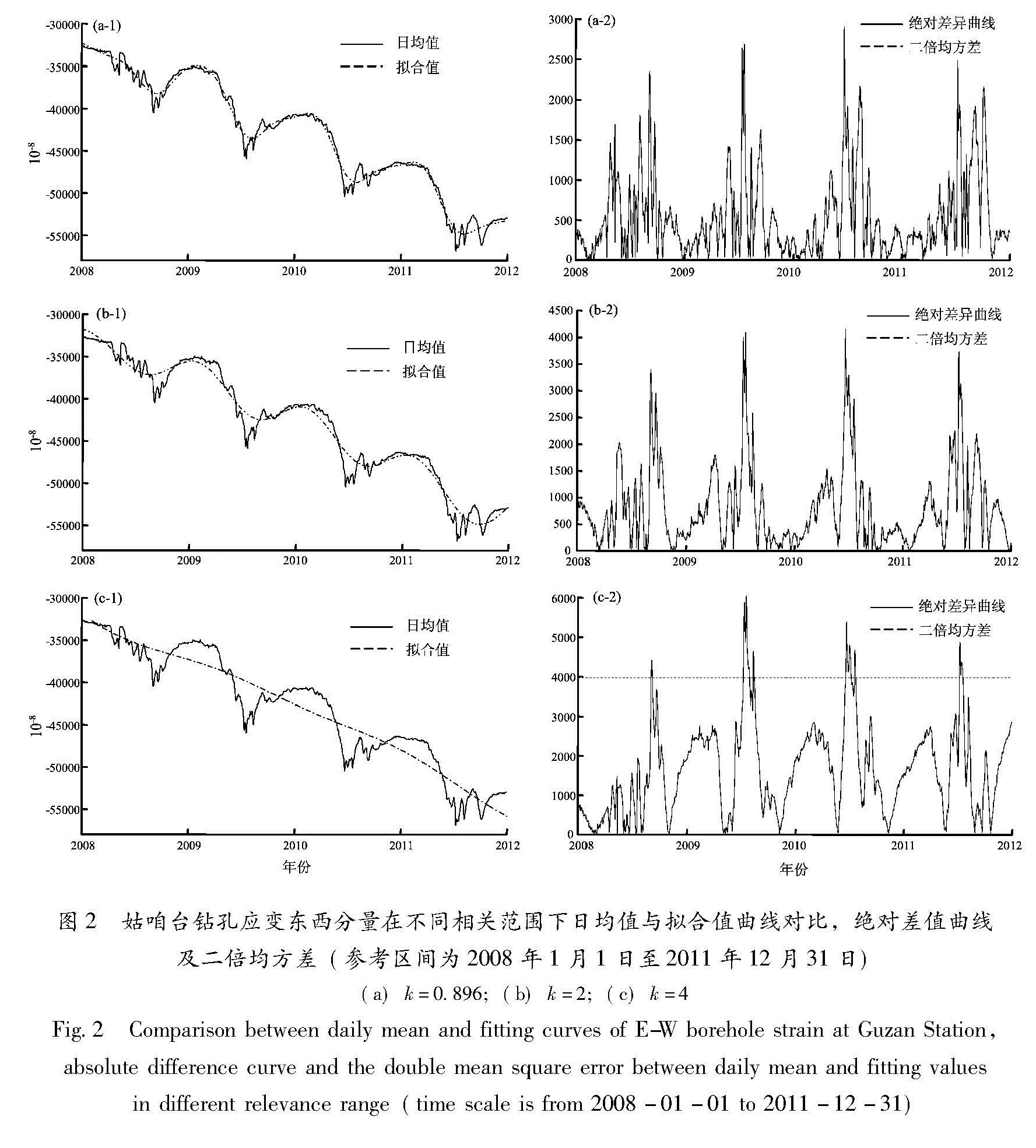
由图2a可以看出,当k值为缺省值0.896,可较好地模拟该测项4年来在总体下降的基础上呈周期性波动的特征,只有在刚起测不久,及2008年5~8月、2009年7~9月、2010年7~8月、2011年7~8月的这些时段差异较大,可能与汶川M8.0、攀枝花M6.1地震、干扰或季节影响等有关。图1 四川姑咱台钻孔应变东西分量日均值观测曲线
Fig.1 Daily mean observation cruve of E-W borehole strain at Guzan Station in Sichuan当选定相关范围为2时,如图2b所示,该拟合曲线总体也呈现下降且周期性的波动,拟合曲线更加平滑,异常程度不显著(超过二倍均方差的也只是2008年5~8月、2009年7~9月、2010年7~8月、2011年7~8月与地震、干扰或季节影响可能有关的时段); 当选定相关范围为4时,则拟合曲线如图2c所示,基本为一条下行的直线,波动起伏不明显,突出反映总体下降趋势,看不出任何异常。由图2可知,最小二乘配置对不同相
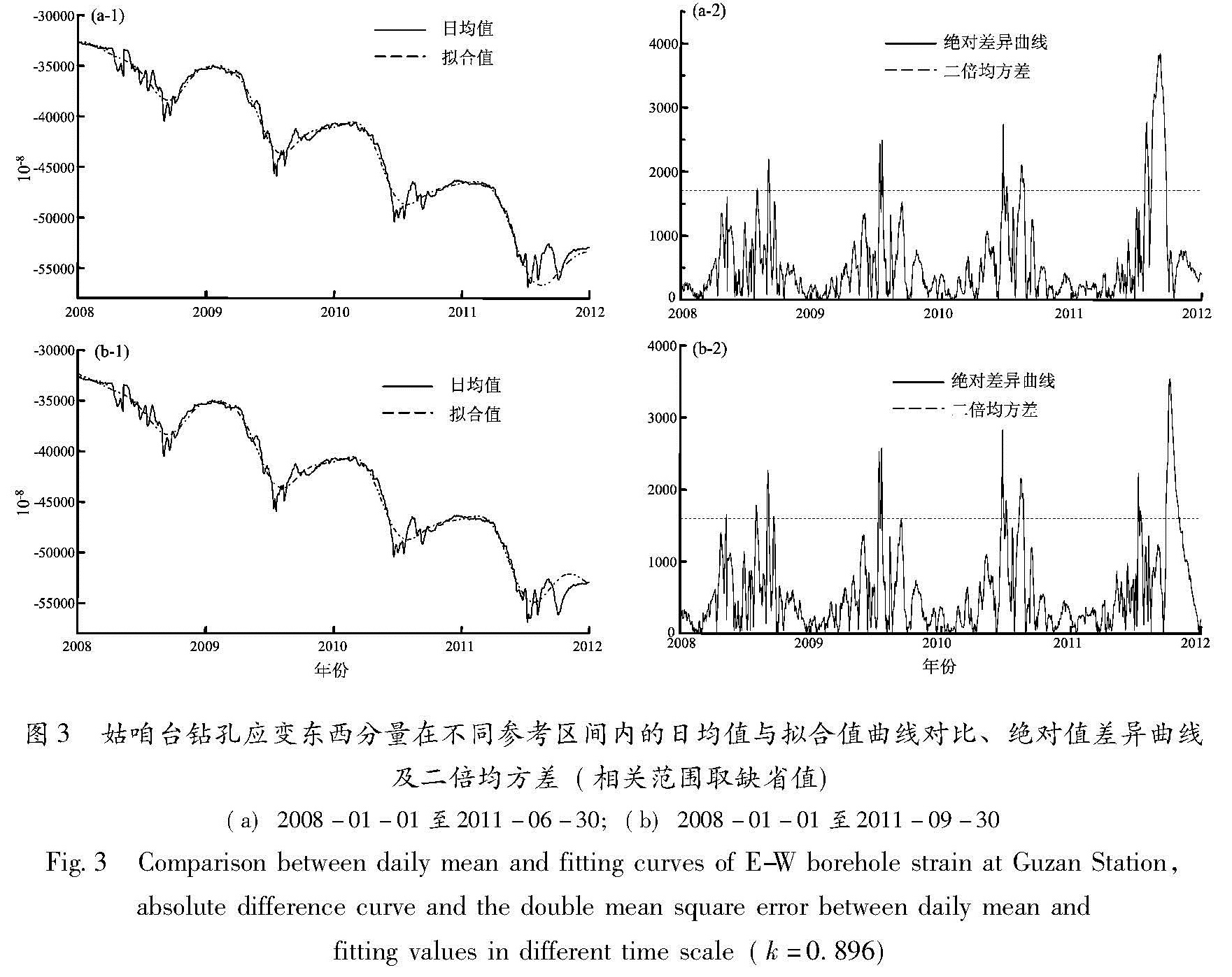
关范围(即不同频段,式(5)中参数随即改变)能反映观测曲线的不同特征信息,与武艳强等(2004)研究结果类似,而从本例可以看出,选取相关范围为缺省值0.896时更适合于定点测项的异常分析。如果认为以往若干年(长时间尺度)变化相对正常或有规律,想借此判定近期变化形态是否与以往正常状态一致、从而识别异常,可根据不同台站资料具体情况选取一定时间段(小于参数k为缺省值的相关范围,本文取小于0.896年的参考区间进行外推。外推的参考区间分别选取为2008年1月1日至2011年6月30日(即外推至2011年下半年)和2008年1月1日至2011年9月30日(即外推至2011年第4季度),外推结果见图3。
从图3a可以看出,2011年7~8月出现的波动陡升更加显著,异常差异明显,对外推结果影响大,但总体年变周期趋势良好; 如果参考区间范围改到2011年9月底结束(图3b),外推效果更佳,总体趋势反应好,说明在相关范围内进行一定时间的外推对判定未知异常存在一定意义。因为姑咱台周期性较好、并无明显异常,外推和实测值的结果符合周期性趋势变化。
fitting values in different time scale(k=0.896)图2 姑咱台钻孔应变东西分量在不同相关范围下日均值与拟合值曲线对比,绝对差值曲线
及二倍均方差(参考区间为2008年1月1日至2011年12月31日)
(a)k=0.896;(b)k=2;(c)k=4
Fig.2 Comparison between daily mean and fitting curves of E-W borehole strain at Guzan Station,absolute difference curve and the double mean square error between daily mean and fitting values in different relevance range(time scale is from 2008-01-01 to 2011-12-31)2.2 趋势加速或转变明显的实例永胜台垂直摆北南分量从2007年至2010年6月总体呈现N向持续倾斜,汶川M8.0地震前出现过下行加速和转折,震后上行加速明显; 攀枝花M6.1地震前有小幅折返,2010年6月前整体波动并不剧烈; 2010年6月出现明显加速,波动至2011年6月,目前南向转折后幅度加大,有一些小的波动或毛刺,可能观测日志与调零、雷电干扰等有关,姚安地震后附近并无中强地震出现,但趋势转折变化特征非常明显。故选云南永胜台“十五”数字前兆观测曲线作为算例二,如图4所示。
计算整个观测时段特征曲线(相关范围为缺省计算值0.896)所得结果如图5a所示。从图中可以看到,拟合曲线较好地模拟4年来时缓、时陡的趋势,拟合曲线总体可以分为两个阶段:2010年6月前上行速度缓慢; 2010年6月后速度加快,转折幅度大。差异比较大的时段出现在2008年的4~5月,2010年的7~8月及2011年年末,可能
受到汶川M8.0地震、雷电和调零的影响,但可以反映出几个时段内的曲线异常变化。图4 云南永胜台垂直摆倾斜北南分量
日均值观测曲线
Fig.4 Daily mean observational records of N-S vertical pendulum tiltmeter at Yongsheng Station in Yunnan进而通过外推求该测项是否存在破年变异常,将参考区间改为2008年至2011年6月底,外推2011年7~12月,如图5b所示。2010年6月的线性加速趋势更加明显,而2011年下半年,尤其9月份以后,测项转折下降趋势与拟合上行加速截
图5 永胜台垂直摆倾斜北南分量在不同参考区间内日均值与拟合值曲线对比、绝对值差异曲线
及二倍均方差(相关范围取缺省值)
(a)2008-01-01至2011-12-31;(b)2008-01-01至2011-06-30;(c)2008-01-01至2011-09-30
Fig.5 Comparison between daily mean and fitting curves of N-S vertical pendulum tiltmeter at Yongsheng Station, absolute difference curve and the double mean square error between daily mean and fitting values in different time scale(k=0.896)然不同; 若参考区间改到2011年9月底结束,外推至2011年10~12月,如图5c所示,2011年7~8月趋势并未改变,而外推的预测结果与实际测项9月转折下行依然相反,说明存在破年变异常。综合分析认为通过最小二乘配置外推能够检验偏离已有数学模型所能描述的部分信息,对辅助判定未知异常有一定意义,但不能作为识别异常的确切指标。
3 结论与讨论
利用最小二乘配置进行定点形变曲线特征模拟和寻找异常特征,可以较好地处理连续变化的点,能够考虑到内插区域内所有已知点的相关性,反映其随时间变化的趋势性。外推时根据时间的相关范围内取一定时段外推,能够辅助识别出定点形变曲线的短、中期趋势变化和异常走势,对于辅助识别定点形变曲线异常有一定的意义。最小二乘配置方法仅是一种数学处理方法,通过滤波和拟合可以处理接近观测误差噪声相对中、高频的部分,可以较好地反应曲线周期,但并不能代替其他如小波分析等滤波数学工具,外推对于异常的最终判定还需其它物理手段予以落实。
- 江在森,张希.2000.华北地区近期地壳水平运动与应力应变场特征[J].地球物理学报,43(5):657-665.
- 孔祥元,郭标明,刘宗泉,等. 2001.大地测量学基础[M].武汉:武汉大学出版社.
- 马超,单新建.2005.昆仑山口西b>S8.0地震INSAR斜距向同震位错分解[J].地震研究,28(3):245-247.
- 陶本藻,周勇前,高士纯,等. 1996.测量平差基础[M].武汉:测绘出版社.
- 武艳强,黄立人. 2004.时间序列处理的新插值方法[J].大地测量与地球动力学,24(4):43-47.
- 武艳强,江在森,杨国华.2007.最小二乘配置方法在提取GPS时间序列信息中的应用[J].国际地震动态,(7):99-103.
- 张希,江在森,张四新.1998.借助最小二乘配置整体解算地壳视应变场[J].地壳形变与地震,18(2):57-62.
- 张希,江在森.1999a.对华北GPS监测区近期地壳应变连续分布的估计[J].地震学刊,75(2):47-52.
- 张希,江在森.1999b.用最小二乘配置获得地形变应变场动态图像的几个问题研究[J].地壳形变与地震,19(3):32-39.