收集郯庐地震带历史强震目录(国家地震局震害防御司,1995; 中国地震局震害防御司,1999; 中国地震局地壳应力研究所,2009)和1970年以来的现代中小地震目录(小震资料来自中国地震台网中心的地震数据库),根据余震的空间窗半径公式lgR=0.48M-1.57(陈凌等,1998)和时间窗表(Console等,1979),确定余震的空间和时间范围,对所收集到的地震目录进行余震删除; 并基于G-R关系的震级—频度分布原理,对研究区的小震资料进行完整性分析(苏有锦等,2003; 王琼等,2011),选取M_L在最小完整震级M_C至5.0级范围内的中小震,利用华北平原地区M_S=1.0112M_L-0.2591公式(谢卓娟,2009)将M_L转换为M_S震级。

通过以上资料预处理,最终给出了郯庐地震带自公元前 70年以来地震4 174次,其中,8级以上地震1次、7.0～7.9级地震6次、6.0～6.9级地震16次、5.0～5.9级地震64次、4.7～4.9级地震38次、4.0～5.0级地震53次、3.0～3.9级地震527次、2.0～2.9级地震3 469次。

分析郯庐地震带地震活动的时间分布特征,以此作为划分累积年平均发生率时段的依据。图1分别给出了该带公元前70年和1400年以来M≥43/4地震的M-T图,从图1a中可以看出,1400年之前仅记有11次地震,地震缺失较多,1400年后地震记录基本完整,1500年以后5级以上地震基本完整(任雪梅,2011); 从图1b中可看出,1400年以来该地震带经历有两个地震活跃期,分别为1477～1687年和1829年至今,郯庐地震带的第一活跃期发生了1668年郯城81/2级特大地震,第二活跃期尚未结束。

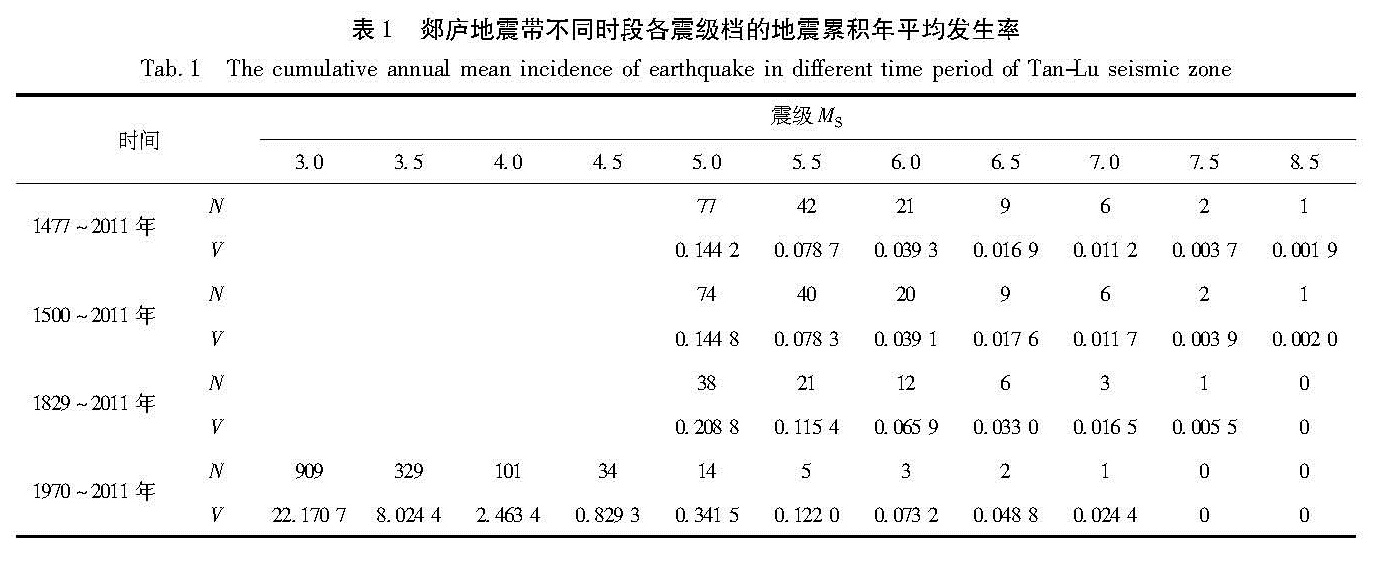
根据郯庐地震带的时间分布特征,分4个统计时段:1477～2011年、1500～2011年、1829～2011年和1970～2011年,分别统计出这4个时段各震级档的地震累积年平均发生率,统计结果如表1所示。

表1 郯庐地震带不同时段各震级档的地震累积年平均发生率
Tab.1 The cumulative annual mean incidence of earthquake in different time period of Tan-Lu seismic zone

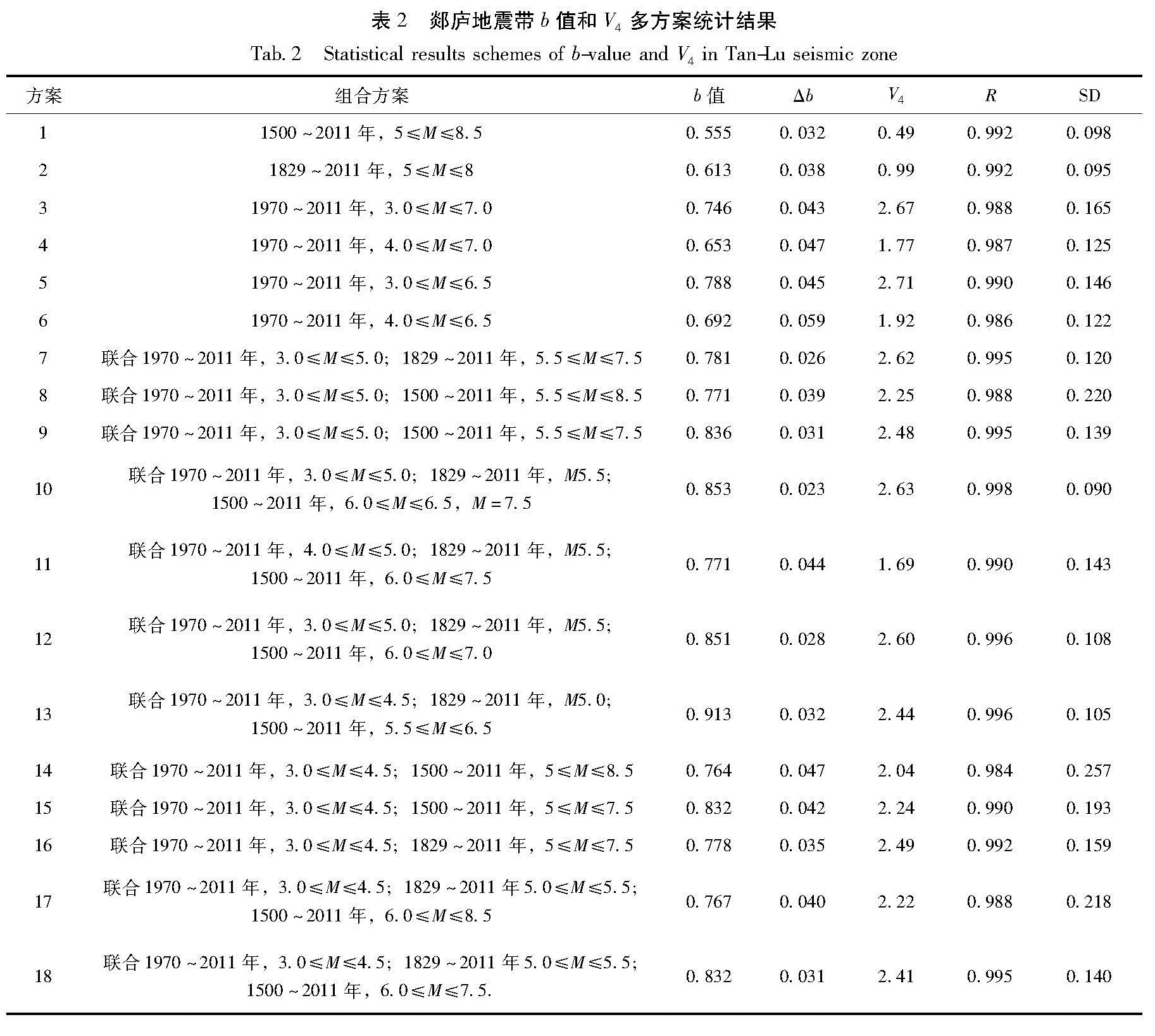
根据郯庐地震带地震样本完备时段、活动期划分、不同震级段等因素,形成多种统计方案,得到多个b值与V₄的组合,每个组合表现出了不同的地震活动特征。统计方案与结果列于表2,表2中“Δ”表示标准离差,R表示拟合的相关系数,SD是回归标准差。本节统计b值时采用0.5作为地震统计间隔(黄玮琼等,1989; 雷建成等,2010)。

图1 公元前70年(a)、公元1400年以来(b)
郯庐地震带的M-T图
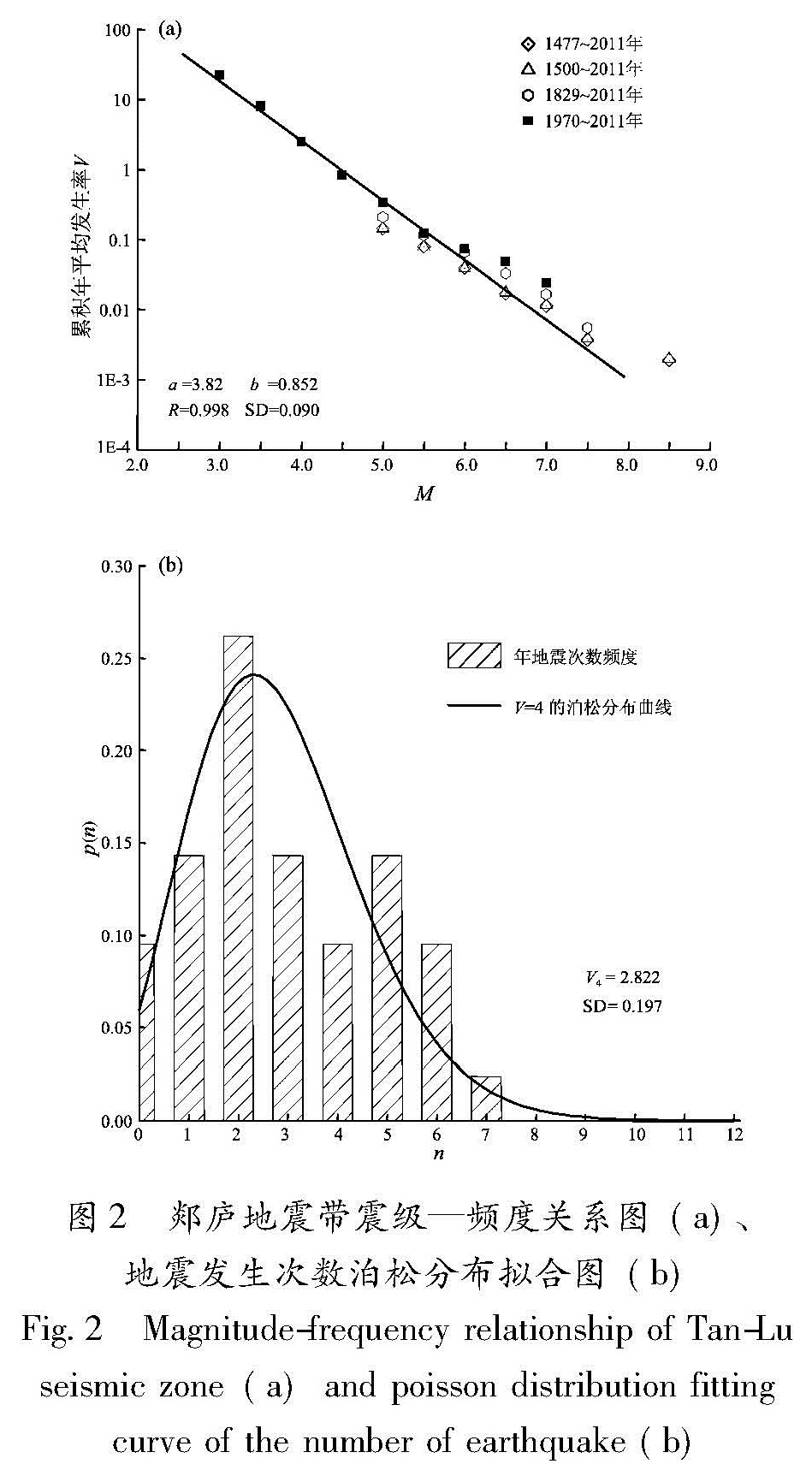
Fig.1 The M-T map of the Tan-Lu seismic zone since 700 BC(a)and 1400(b)

表2中各统计方案的拟合相关系数R均达到0.984以上,按照10号方案进行拟合的相关系数最高,R为0.998,R→1,表明按照10号方案进行拟合的效果最佳,线性关系最好,回归标准差SD=0.090,也为方案中的最低值,数据可靠性高。按照10号方案进行拟合得到的b=0.853,拟合结果如图2a所示。

表2 郯庐地震带b值和V4多方案统计结果
Tab.2 Statistical results schemes of b-value and V4 in Tan-Lu seismic zone

图2 郯庐地震带震级—频度关系图(a)、地震发生次数泊松分布拟合图(b)
Fig.2 Magnitude-frequency relationship of Tan-Lu seismic zone(a)and poisson distribution fitting curve of the number of earthquake(b)

根据郯庐地震带的b值和V₄统计结果,并基于不低估已有的地震危险性,同时对未来地震危险性给予合理保守考虑的原则^①,最终确定郯庐地震带b=0.856,V₄=2.822。

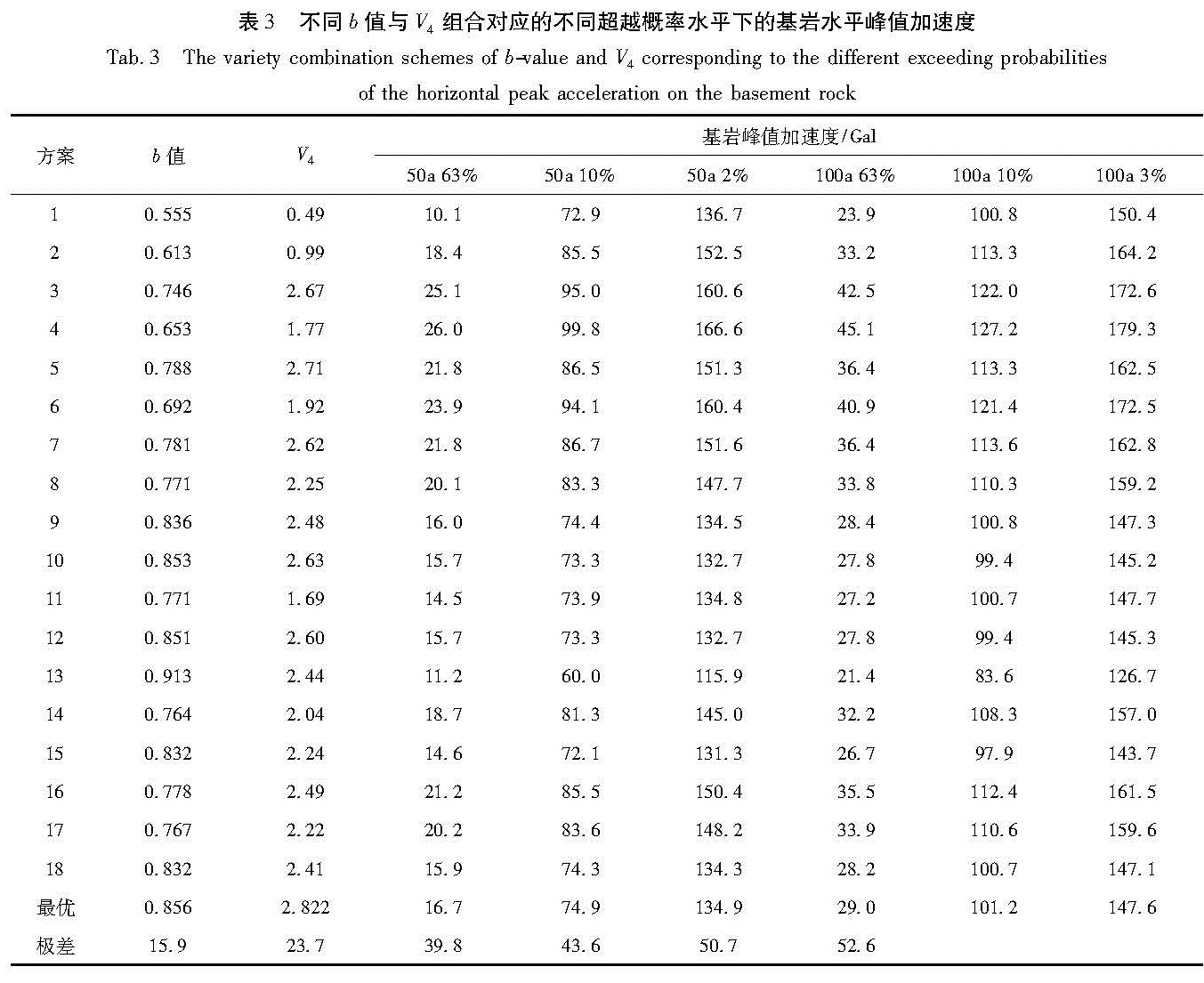
将不同b值与V₄的组合作为概率危险性分析中的计算参数,以相同的潜在震源区划分方案、空间分布函数和地震动衰减模型(GB18306-2001; 卢寿德,2005),采用考虑地震活动时空不均匀特性的概率危险性分析方法(CPSHA),计算统计区内不同超越概率水平下的地震加速度峰值。随机选取点(35.446°N,119.290°E),表3给出该点在不同b值与V₄组合计算得到的50 a超越概率分别为63%、10%、2%和100年超越概率分别为63%、10%、3%的地震基岩水平峰值加速度。

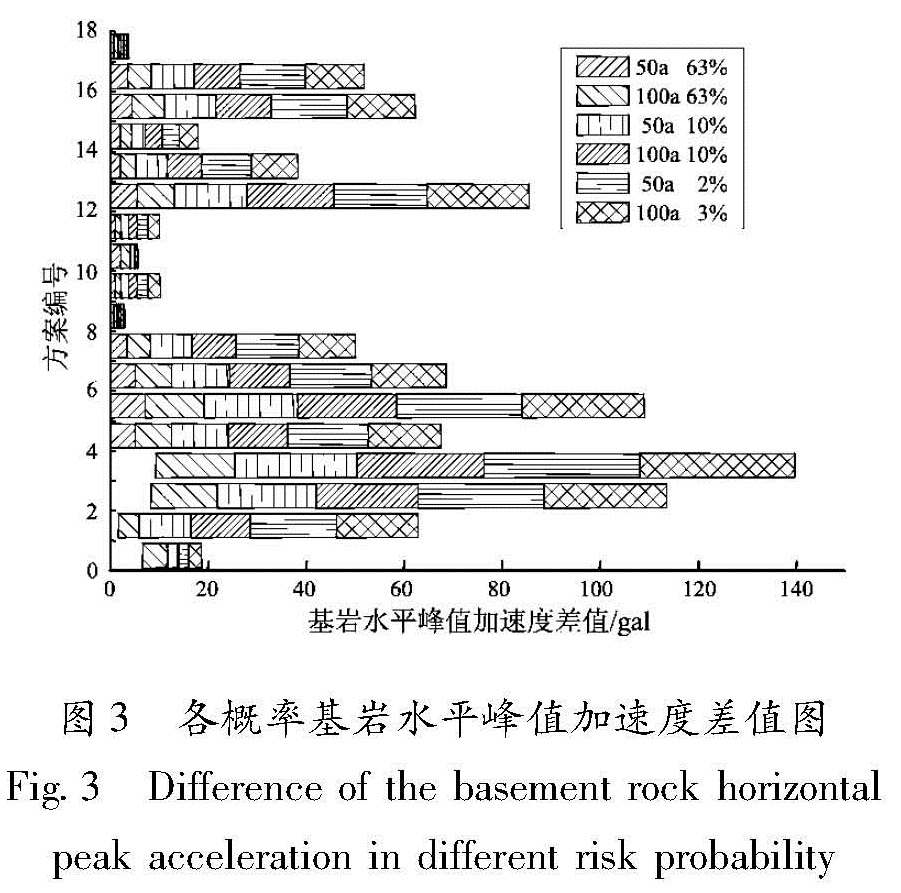
根据表3,以最优b值和V₄计算得到的基岩水平峰值加速度值为参照标准,计算各方案的基岩水平峰值加速度值与参照值的差值,将各概率基岩水平峰值加速度差值绘制成图3。结合表3、图3可看出:① 使用不同的b值与V₄组合计算得到的不同超越概率水平下的基岩水平峰值加速度值有明显差异,但其变化具有一定的规律性; ② 不同的b值与V₄组合的变化对高超越概率水平的影响均大于对低超越概率水平的影响,如图3所示,各方案中50 a超越概率为2%、100 a超越概率为3%的基岩水平峰值加速度差值均大于低概率的

图3 各概率基岩水平峰值加速度差值图
Fig.3 Difference of the basement rock horizontal peak acceleration in different risk probability

表3 不同b值与V4组合对应的不同超越概率水平下的基岩水平峰值加速度
Tab.3 The variety combination schemes of b-value and V4 corresponding to the different exceeding probabilities of the horizontal peak acceleration on the basement rock

50 a超越概率为63%、100a超越概率为63%; 表3显示了18种方案计算结果的极差,可看出,极差也随着超越概率水平的增加而增加,变化范围在15.9～52.6 Gal之间; ③ b值拟合时,相关系数高,线性关系好的拟合方案计算得到的各概率基岩水平峰值加速度差值较小,如:9、10、11等方案,相反,拟合线性关系差的方案计算得到的各概率基岩水平峰值加速度差值大,变化幅度大,如3、4、6方案。

综上所述,b值和V₄的不确定性影响到地震危险性分析的结果,特别是对高超越概率的影响不可忽略,在b值和V₄统计时,应根据地震统计区样本资料的完整性,选取合适的统计时段、采用合适的样本处理方法联合确定统计方案。

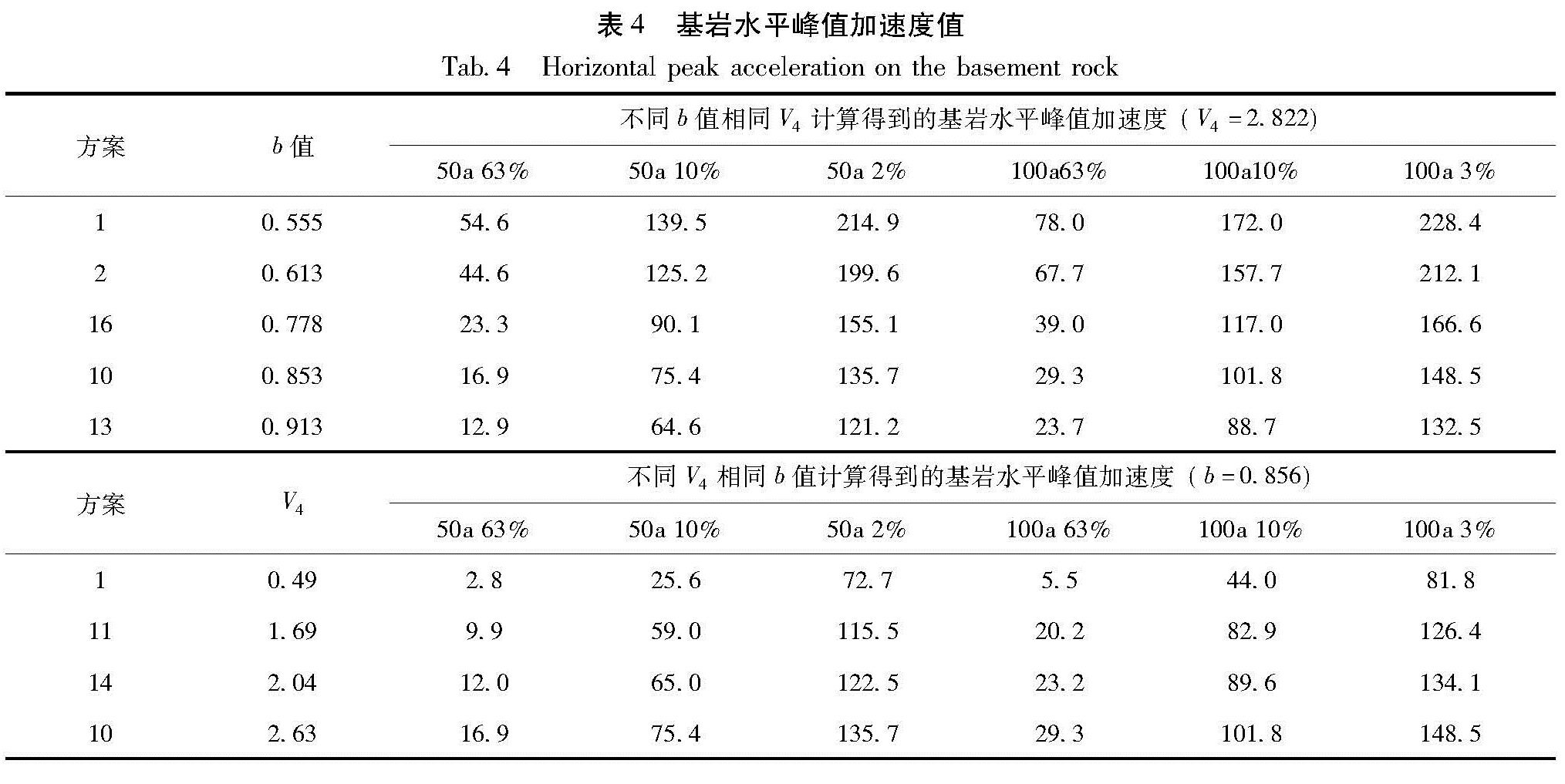
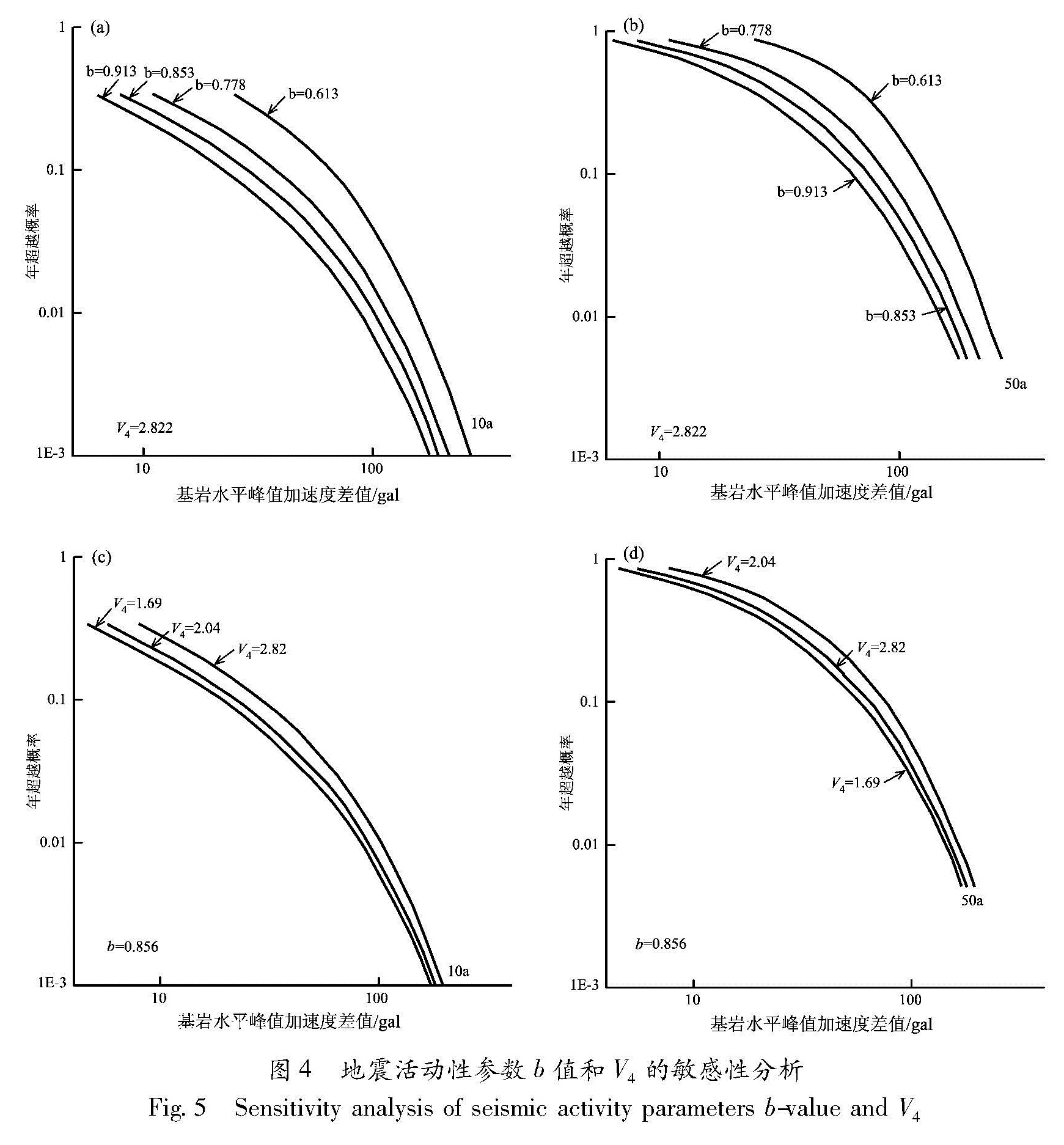
为了进一步研究b值和V₄对地震危险性分析结果的影响程度,判断较为敏感的参数,我们分别计算该场点在V₄一定(V₄=2.822)、b值变化和b值一定(b=0.853)、V₄值变化两种情况下的各概率基岩水平加速度峰值,计算结果如表4所示,图4为其基岩水平峰值加速度超越概率曲线图(超越概率分别为10 a、50 a)。

结合表4和图4可看出:① V₄一定时,地震危险性分析的结果随b值的增加而减小,b值一定时,地震危险性分析的结果随V₄的增加而增加; 说明b值越大,危险性程度越小,V₄越大,危险性程度越大,计算结果合理。② 图4中显示,超越概率曲线的形状基本一致,变化规律一致,但高超越概率段的曲线比较离散,低超越概率段曲线较为集中,这说明地震活动性参数的变化对高超越概率水平的影响大于对低超越概率水平的影响,与上节分析结果一致。③ 对比图4a～d高超越概率和低超越概率段可看出,图4a、b中曲线的离散程度明显大于图4c、d中曲线的离散程度,反映出b值和V₄的敏感性,b值的变化对计算结果影响更大,较为敏感,V₄的敏感性相对较弱。

表4 基岩水平峰值加速度值
Tab.4 Horizontal peak acceleration on the basement rock

图4 地震活动性参数b值和V4的敏感性分析
Fig.5 Sensitivity analysis of seismic activity parameters b-value and V4