基金项目:国家自然科学基金重点项目(40534021)资助.
(1.长安大学 地质工程与测绘学院,陕西 西安 710054; 2.中国地震局第二监测中心,陕西 西安 710054)
(1.School of Geological Engineering and Geomatics,Chang'an University,Xi'an 710054,Shannxi,China)(2.The Second Monitoring and Application Center,CEA,Xi'an 710054,Shannxi,China)
explosion vibration; Hilbert-Huang transform; time-frequency analysis
备注
基金项目:国家自然科学基金重点项目(40534021)资助.
利用小波变换、S变换、Wigner-ville分布(WVD)和Hilbert-Huang变换(HHT)对模拟信号进行时频分析并比较,结果表明基于经验模态分解的HHT具有更强的适应性,能较为准确地提取信号的时变特征。利用HHT对实际记录的宽频带爆破振动信号进行了时频分析,其结果较为准确地描述了信号的时变特征。
We compare the time-frequency spectrums of analog signal which was determined by continuous wavelet transform(CWT),S-transform,Wigner-Ville distribution(WVD)and Hilbert-Huang transform(HHT). The results show that HHT based on empirical mode decomposition(EMD)has higher adaptability and can accurately extract the time-frequency characteristics of the explosion signal. Then we analyze time-frequency spectrum of broadband explosion vibration signal in actual by HHT,and time-frequency analysis results accurately described the time varying characteristics of the explosion vibration signal.
引言
地震波波形是具有时变特性的非线性、非平稳信号,使得对地震波的分析方法受到某些限制。传统上,傅立叶频谱提供了一个简单的方法求得“能量—频率”分布,但它要求系统必须是线性的,而且资料必须是周期性的或是平稳的,否则求得的频谱就没有物理意义。近十几年来,使用最多的是小波分析法(Basu,Gupta,2001; Shan et al,2009; Spanos et al,2005; 曹晖等,2002),可进一步求得“能量—频率—时间”分布,然而本质上,小波分析法由在傅立叶频谱分析法的一些假设基础上推论而来,仍然具有原方法的限制与缺点。为了突破傅立叶分析法的限制,Huang等(1998)年提出了一种非线性、非平稳信号分解方法——经验模态分解(Empirical Mode Decomposition method,简称EMD),该方法基于信号本身的时间尺度特征,把复杂的信号分解为有限个固有模态分量(Intrinsic Mode Functions,简称IMF)和一个余项,每一项IMF分量都适用希尔伯特变换,由此可计算瞬时频率,因此就可同时在频率轴及时间轴上讨论一事件,称为希尔伯特—黄变换方法(Hilbert-Huang Transform method,简称HHT)。HHT是一种自适应的信号处理方法,比传统的傅立叶分析和依赖于先验基的小波分析等方法更适用于非线性、非平稳信号分析(Huang et al,1998; Wu,Huang,2009; )。目前,此方法已广泛应用于目标识别、结构损伤诊断、信号去噪、地震信号(Li,Chi,2008; Lin,Wang,2006; 方嘉治等,2012; 钱昌松等,2010; 王彬等,2005)和爆破信号分析等方面(李夕兵等,2005,2006; 张义平等,2005)。
笔者利用小波变换、S变换、Wigner-ville分布和Hilbert-Huang变换(HHT)对模拟信号和陕西数字地震台网记录的宽频带爆破振动信号进行了时频分析,比较了这些方法的优缺点和适用范围。
1 时频分析方法
1.1 小波变换小波变换是一种窗口面积固定但形状可以改变,即时间窗和频率窗都可改变的时频局部化分析方法。对于任意的函数或信号,小波变换定义为
Wf(a,b)=∫Rf(x)φa,b^-(x)dx
=1/((|a|)1/2)∫Rf(x)Ψ^-((x-b)/a)dx.(1)
其中,Ψ(x)为基本小波函数或母小波函数,在实际应用中需要选择小波基,所选小波基函数在具有紧支撑性和一定正则性的同时,还需外形与被分析的对象有一定的相似性,本文选用Morlet小波。
1.2 S变换S变换是以Morlet小波为基本小波的连续小波变换的延伸。在S变换中基本小波由简谐波与高斯函数的乘积构成,基本小波中的简谐波在时间域仅作伸缩变换,而高斯函数则进行伸缩和平移,故可认为是连续小波变换的“相位校正”。函数的S变换表示为
Sf(t,f)=∫Rh(τ)·(|f|)/((2π)1/2)·exp((-(τ-t)2f 2)/2)·exp(-i2πfτ)dτ.(2)
其中,(|f|)/((2π)1/2)·exp((-(τ-t)2f 2)/2)定义为母波; exp(-i2πfτ)为相位因子。
S变换以高斯视窗为基底函数来回移动,可以分析时频域特征,虽然直接和傅立叶相关,但S变换的优点是其局部化的高斯视窗可以将信号详细转换,提高了在频率域的解析度(Pinnegar,2005; Stockwell et al,1996; 樊剑等,2008)。
1.3 Wigner-Ville分布(WVD)Wigner-Ville分布首先由Wigner提出,用于量子力学领域问题研究,后由Ville引入到信号分析领域。它有很多优良的数学性质,且表达式直观简单。对于信号,其Wigner-Ville分布为(科恩,1998)
WVDx(t,f)=∫+∞-∞x(t+τ/2)x*(t-τ/2)e-i2πfτdτ.(3)
1.4 Hilbert-Huang变换Hilbert-Huang变换首先用经验模态分解(EMD),将信号分解为若干IMF,然后进行Hilbert变换,将实数信号配上虚部,得到解析信号,再根据解析信号的相位随时间的改变而得到瞬时频率。
EMD方法根据数据本身的特征进行分解,将信号分解成一组稳态的数据序列集,即IMF分量模式。EMD方法通过特征时间尺度来获得IMF分量筛分过程,将原始信号分解成n个imf分量和一个残余分量,将信号从高频到低频的顺序依次分解。即:
x(t)=∑ni=1imfi(t)+rn.(4)
对于任一IMF分量Cj(t)作Hilbert变换,得到一个复IMF分量Zj(t), aj(t)表示复IMF的振幅,θj(t)表示相位,瞬时频率ωj(t)=(dθj(t))/(dt)。因此可得到Hilbert谱为:
H(ω,t)=Re∑ni=1aj(t)ei∫ωj(t)dt.(5)
可见,HHT谱精确地描述了信号的幅值随时间和频率的变化规律,HHT方法具有较好的自适应性和频率瞬时性,对信号的非线性反映能力较好且对稳态和非稳态信号都能进行分析,适合分析具有非线性和非平稳动态变化特征的信号。
2 仿真实验
假设模拟信号s为4个余弦叠加信号,其表达式为
s(t)=cos(2πf1t)+cos(2πf2t)+cos(2πf3t)+cos(2πf4t).(6)
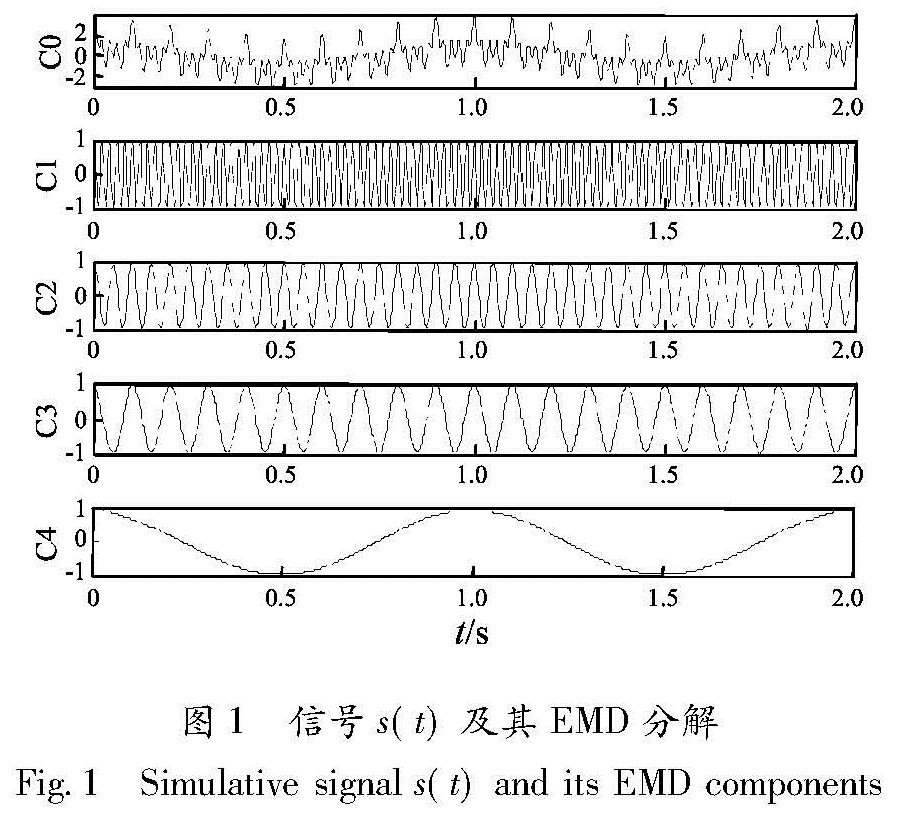
其中,f1=1 Hz,f2=10 Hz,f3=20 Hz,f4=50 Hz,数据采样频率为500 Hz,样本数据为1000个,对s(t)进行EMD分解,得到结果如图1所示。
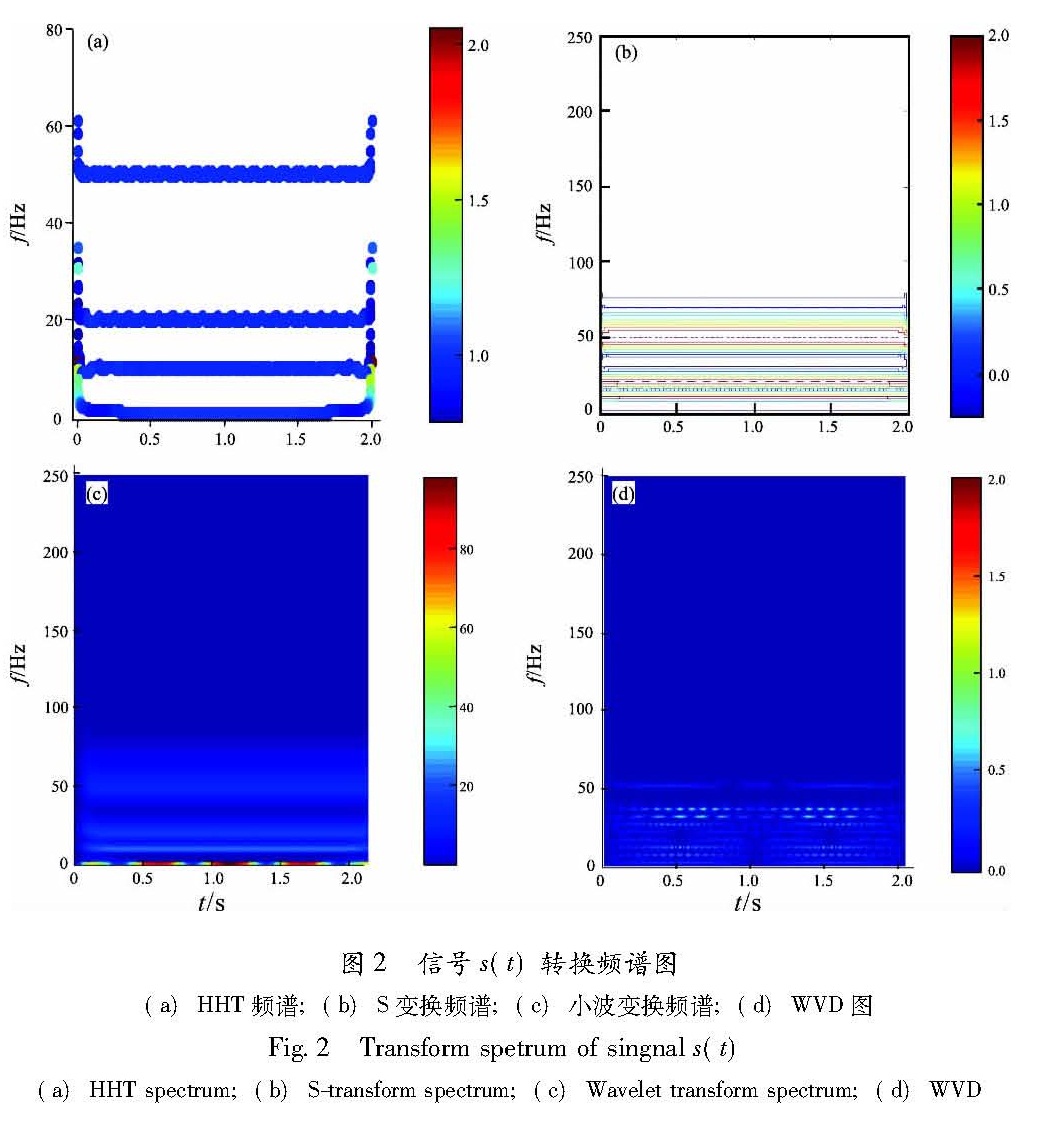
由图1可见,C0为原始信号,C1、C2、C3、C4为用EMD分解得到的4个分量。可见,EMD分解是信号本身所决定的一个自适应分解过程,能很快地提取信号特征并分解出信号的分量,分解出的4个IMF分量正是仿真信号的4个原始信号,表明了分解的可靠性、高效性,体现了IMF分量本身的物理含义。图2为信号s(t)的HHT频谱图、S变换频谱图、小波变换频谱图和WVD图。由图可见,HHT准确地提取了信号的时频特征,通过S变换亦较好地提取了信号的特征,较好地分解出了仿真信号的4个原始信号,但其分辨率低于HHT,小波变换则存在漏能现象,频率分辨率明显低于HHT和S变换,Wigner-Ville分布具有良好的时频聚集性,但由于交叉干扰项的影响,出现了虚假频率成分。
3 爆破振动信号时频分析
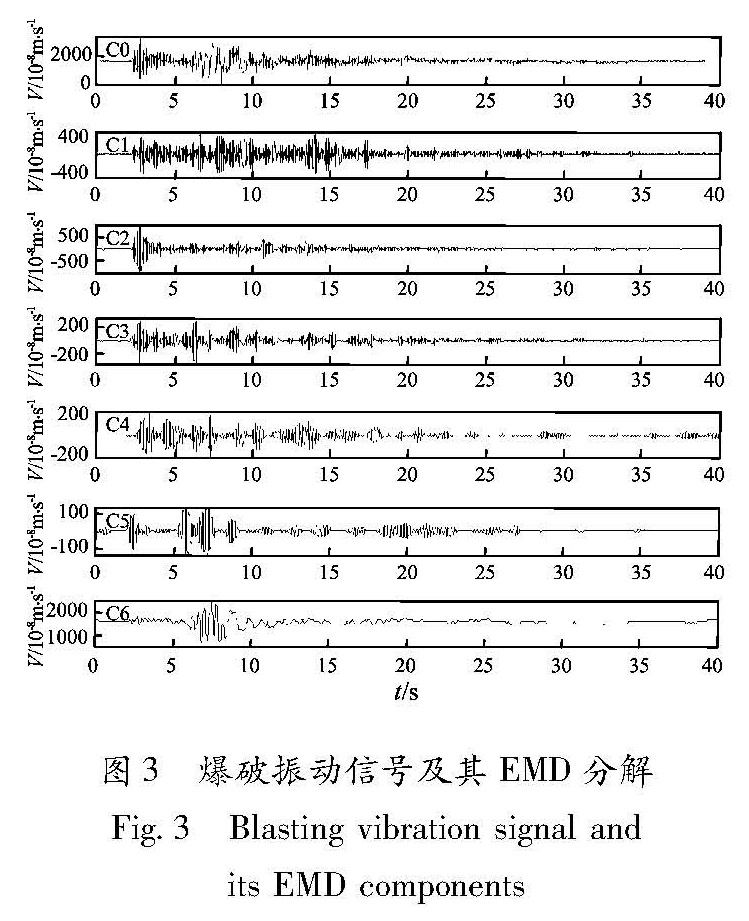
实际记录取自华阴地震台记录到的爆破振动信号,采用FBS-3B型宽频带数字地震计,频带范围为0.05~20 s,采样率为每秒50个样点。图3为爆破振动信号的原始曲线(C0)和EMD分解图(C1~C6)。可见,EMD分解较好地分离了P波段和Rg波段,爆破振动信号可分为4个变化比较明显的阶段:① 爆破发生前的地脉动记录阶段。此时爆破还没有发生,在时频图上能量谱值接近于0。② P波阶段。能量从无到有,特别对P波初动的突变性,被精确地刻划出来,但能量值不是很大。③ Rg波阶段。这个阶段是一个渐变过程,Rg波初动的突变性被较精确地刻划出来,能量远大于其它部分,是地震能量释放的主要阶段。④ 尾波持续阶段。含有一定能量,相对较弱,变化不稳,可能是介质散射造成的。⑤ 爆破振动结束阶段。爆破振动能量基本消失,又回到正常地脉动记录阶段。
图4为爆破振动信号的HHT时频图。由图可见,HHT时频图清晰而详细地显示了能量随时频的具体分布。可较清晰地识别爆破振动信号在时频域中的几个峰值,最大峰值频率为2.5 Hz,发生的时间是7.5 s左右,峰值频率为1Hz和6Hz的发生的时间在是9 s左右,峰值频率为10 Hz信号的发生时间在是2.5 s左右,峰值频率为15Hz信号的发生时间则在2.5、7.5和9 s左右; 还可看出,大致在17 s后,低频段的能量超过了高频段,在25 s,高频段的能量显著减弱。4 讨论与结论
利用模拟信号,对小波变换、S变换、Wigner-ville分布(WVD)和Hilbert-Huang变换(HHT)的时频分析进行了比较,结果表明基于经验模态分解的HHT具有更强的适应性,无需事先确定分解阶次,不受人为因素影响,能较为准确地提取信号的时变特征。利用HHT对实际记录的宽频带爆破振动信号进行了时频分析,其结果较为准确地描述了信号的时变特征。
- 曹晖,赖明,白绍良. 2002. 基于小波变换的地震地面运动仿真研究[J]. 土木工程学报,35(4):41-46.
- 樊剑,吕超,张辉. 2008. 基于S变换的地震波时频分析及人工调整[J]. 振动工程学报,21(4):381-386.
- 方嘉治,赵志伟,蔡宗文,等. 2012.古田地震水口水电站重力坝强震观测记录HHT分析[J]. 地震研究,35(2):236-239.
- 李夕兵,张义平,刘志祥,等. 2005.爆破震动信号的小波分析与HHT变换[J]. 爆炸与冲击,25(6):528-534.
- 李夕兵,张义平,左宇军,等. 2006.岩石爆破振动信号的EMD滤波与消噪[J]. 中南大学学报(自然科学版),37(1):150-154.
- 钱昌松,刘代志,刘志刚,等. 2010.基于递归高通滤波的经验模态分解及其在地震信号分析中的应用[J]. 地球物理学报,53(5):1215-1225.
- 王彬,杨润海,郭梦秋,等. 2005. 昆明高层建筑强震观测记录HHT分析[J].地震研究,28(1):78-81.
- 张义平,李夕兵,赵国彦.2005.基于HHT方法的爆破地震信号分析[J]. 工程爆破,11(1):l-7.
- Basu B,Gupta V K. 2001. Wavelet-based stochastic seismic response of a duffing oscillator[J]. Journal of Sound and Vibration,245(2):251-260.
- Huang N E,Shen Z,Long S R. 1998. The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society of London,Series A,454:903-995.
- 科恩L. 1998. 时频分析:理论与应用[M]. 白居宪,译. 西安:西安交通大学出版社.
- Li X,Chi H. 2008.Echo analysis of objects on the seafloor[J]. The Journal of the Acoustical Society of America,123(5):4803-4807.
- Lin Z S,Wang S G. 2006. EMD analysis of solar insolation[J].Meteorol Atmos Phys,93:123-128.
- Pinnegar C R. 2005.Time-frequency and time-time filtering with the S-transform and TT-transform[J]. Digital Signal Processing,15(5):604-620.
- Shan H,Ma J,Yang H. 2009.Comparisons of wavelets,contourlets,and curvelets in seismic denoising[J]. Journal of Applied Geophysics,69(2):103-115.
- Spanos P D,Tezcan J,Tratskas P. 2005.Stochastic processes evolutionary spectrum estimation via harmonic wavelets[J]. Computer Methods and Application Mechanics Engineering,194(12):1 367-1 383.
- Stockwell R G,Mansinha L,Lowe R P. 1996.Localization of the complex spectrum:The S transform[J]. IEEE Transactions on Signal Processing,44(4):998-1001.
- Wu Z,Huang N E. 2009. Ensemble empirical mode decomposition:noise assisted data analysis method[J]. Advance in Adaptive Data Analysis,1:1-41.