地震研究

云南中小地震矩震级的测定^*

杨晶琼,刘丽芳,杨周胜

(云南省地震局,云南昆明 650224)

关键词：中小地震; 震源波谱参数; 地震矩; 矩震级; 回归分析法

Measurement on Moment Magnitude of Moderate and Small Earthquakes in Yunnan

YANG Jing-qiong,LIU Li-fang,YANG Zhou-sheng

(Earthquake Administration of Yunnan Province,Kunming 650224,Yunnan,China)

Keywords：moderate and small earthquake; source spectrum parameter; seismic moment magnitude; regression analysis method

备注

收稿日期:2013-03-04
基金项目:中国地震局“测震台网青年骨干培养专项”(20120104)资助.

摘要

全文

图/表

参考文献

利用云南省测震台网的数字地震波形资料,反演了2008年1月至2012年9月675个中小地震的震源波谱参数,并计算了这些地震的地震矩M₀和矩震级M_W,最后利用回归分析方法得到了近震震级M_L和M_W之间的关系式。

Based on digital seismic waveform data in Yunnan seismic network,we inversed the source spectrum parameters and calculated the seismic moment M₀ and moment magnitude M_W of 675 moderate and small earthquakes form Jan.,2008 to Sep.,2012. Finally,we obtained the relationship expression between body wave magnitude M_L and moment magnitude M_W of local earthquake by linear regression analysis method.

引言
1 计算方法
2 资料选取
3 M_L和M_W回归关系
4 结论

图1 研究区台站、地震震中及射线路径分布图<br/>Fig.1 Distribution of seismic stations,earthquake epicenters and ray path in study area

图1 研究区台站、地震震中及射线路径分布图
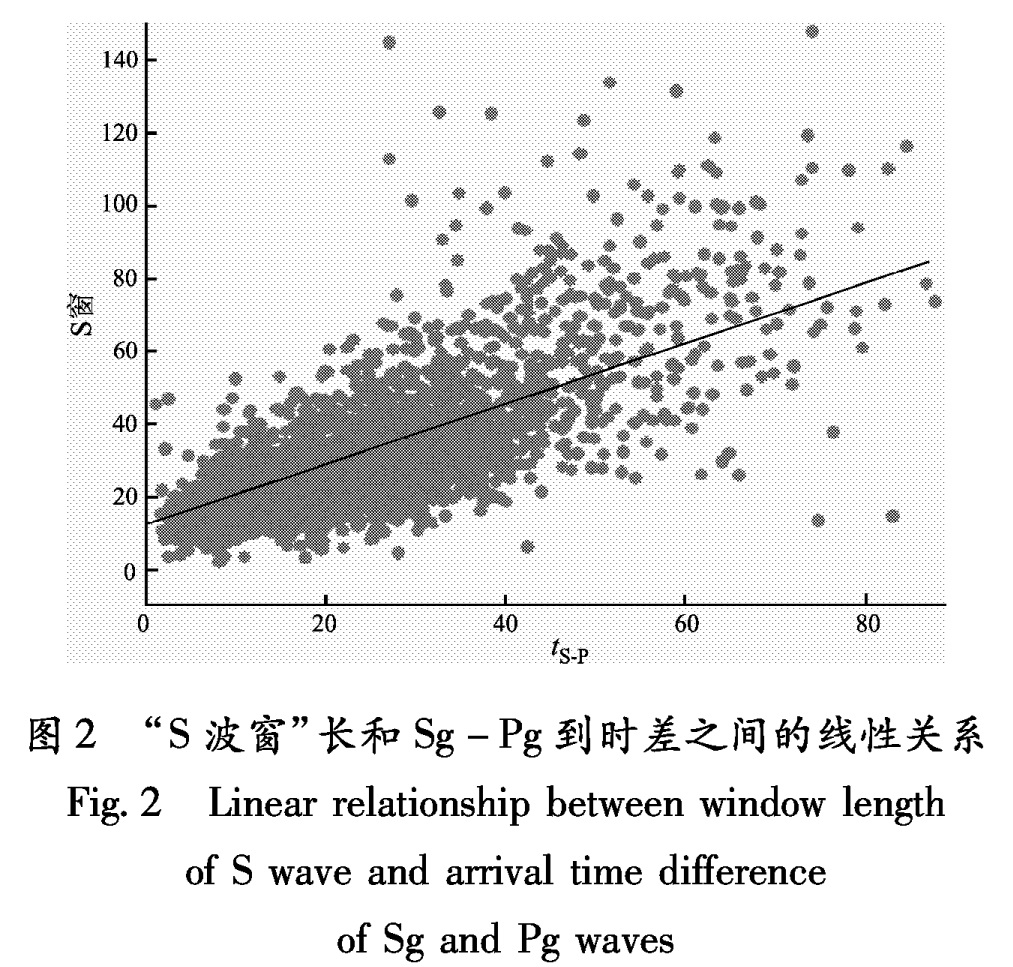
Fig.1 Distribution of seismic stations,earthquake epicenters and ray path in study area

图2 “S波窗”长和Sg-Pg到时差之间的线性关系<br/>Fig.2 Linear relationship between window length of S wave and arrival time difference of Sg and Pg waves

图2 “S波窗”长和Sg-Pg到时差之间的线性关系
Fig.2 Linear relationship between window length of S wave and arrival time difference of Sg and Pg waves

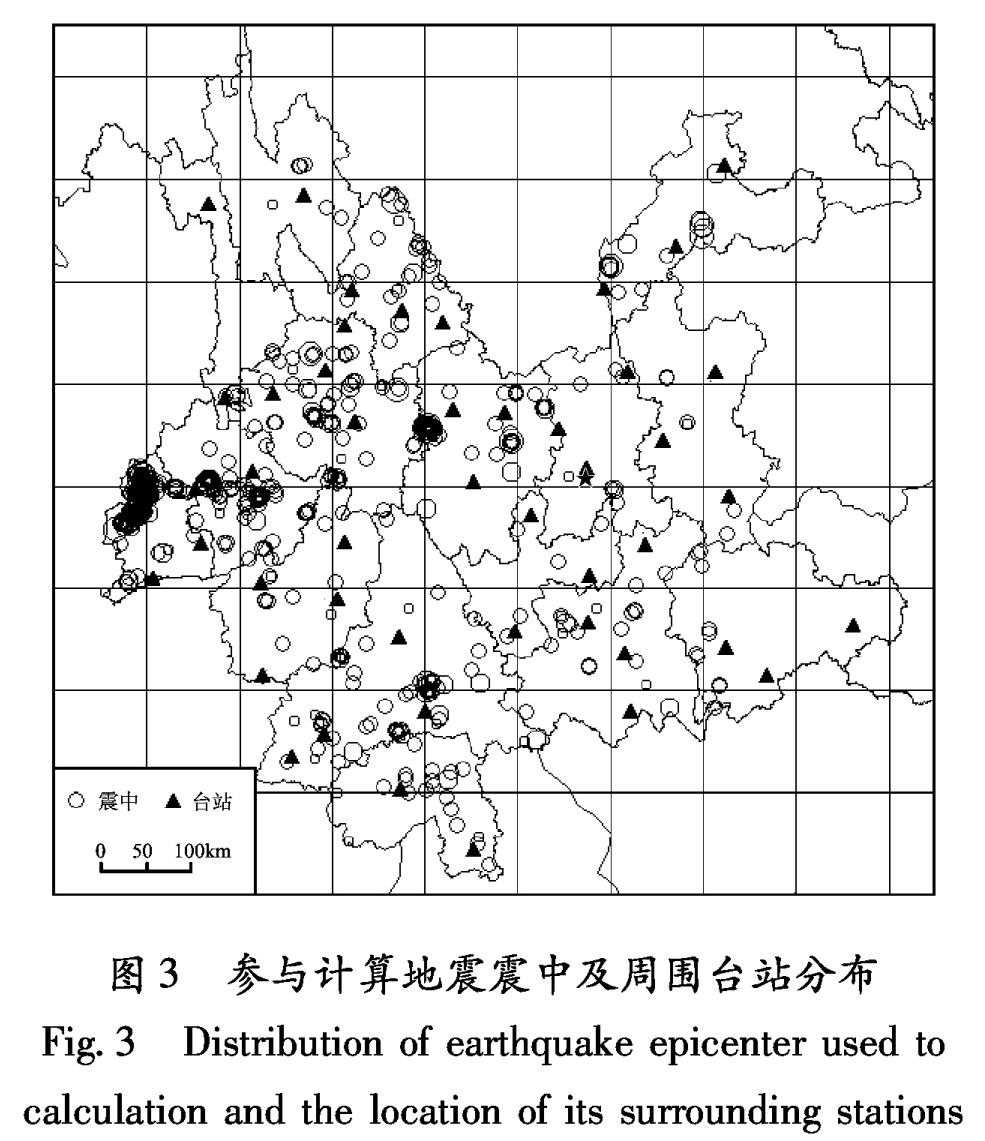
图3 参与计算地震震中及周围台站分布<br/>Fig.3 Distribution of earthquake epicenter used to calculation and the location of its surrounding stations

图3 参与计算地震震中及周围台站分布
Fig.3 Distribution of earthquake epicenter used to calculation and the location of its surrounding stations

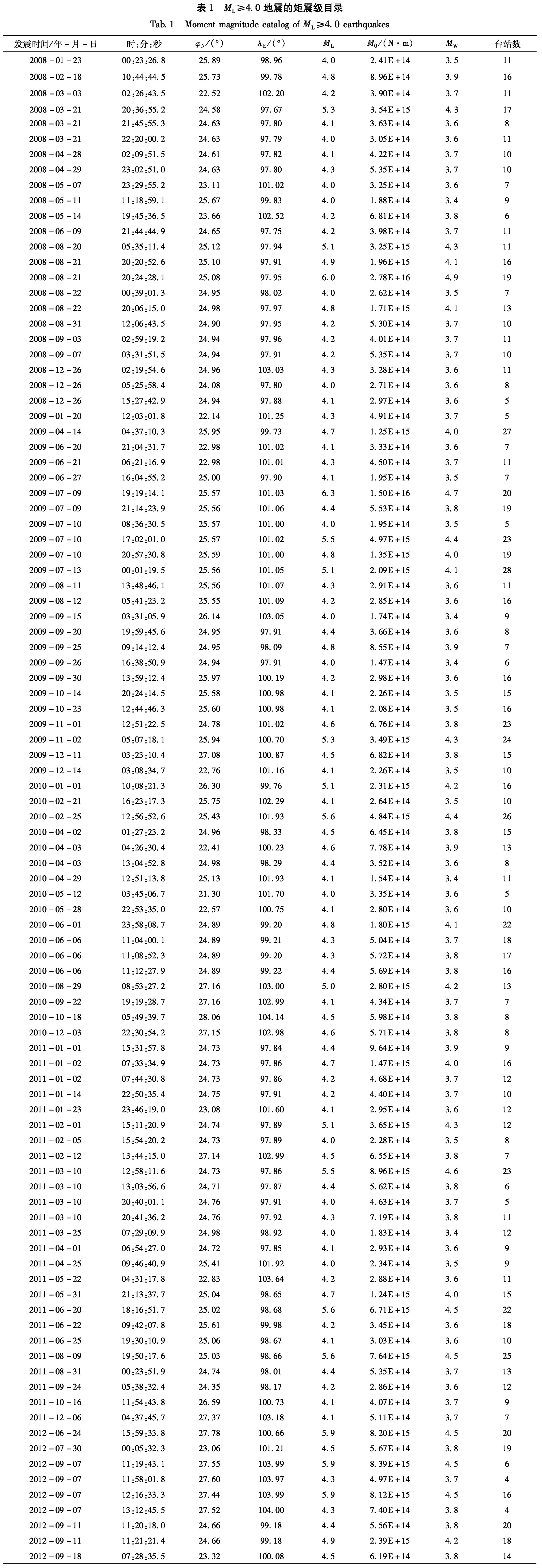
表1 ML≥4.0地震的矩震级目录<br/>Tab.1 Moment magnitude catalog of ML≥4.0 earthquakes

表1 ML≥4.0地震的矩震级目录
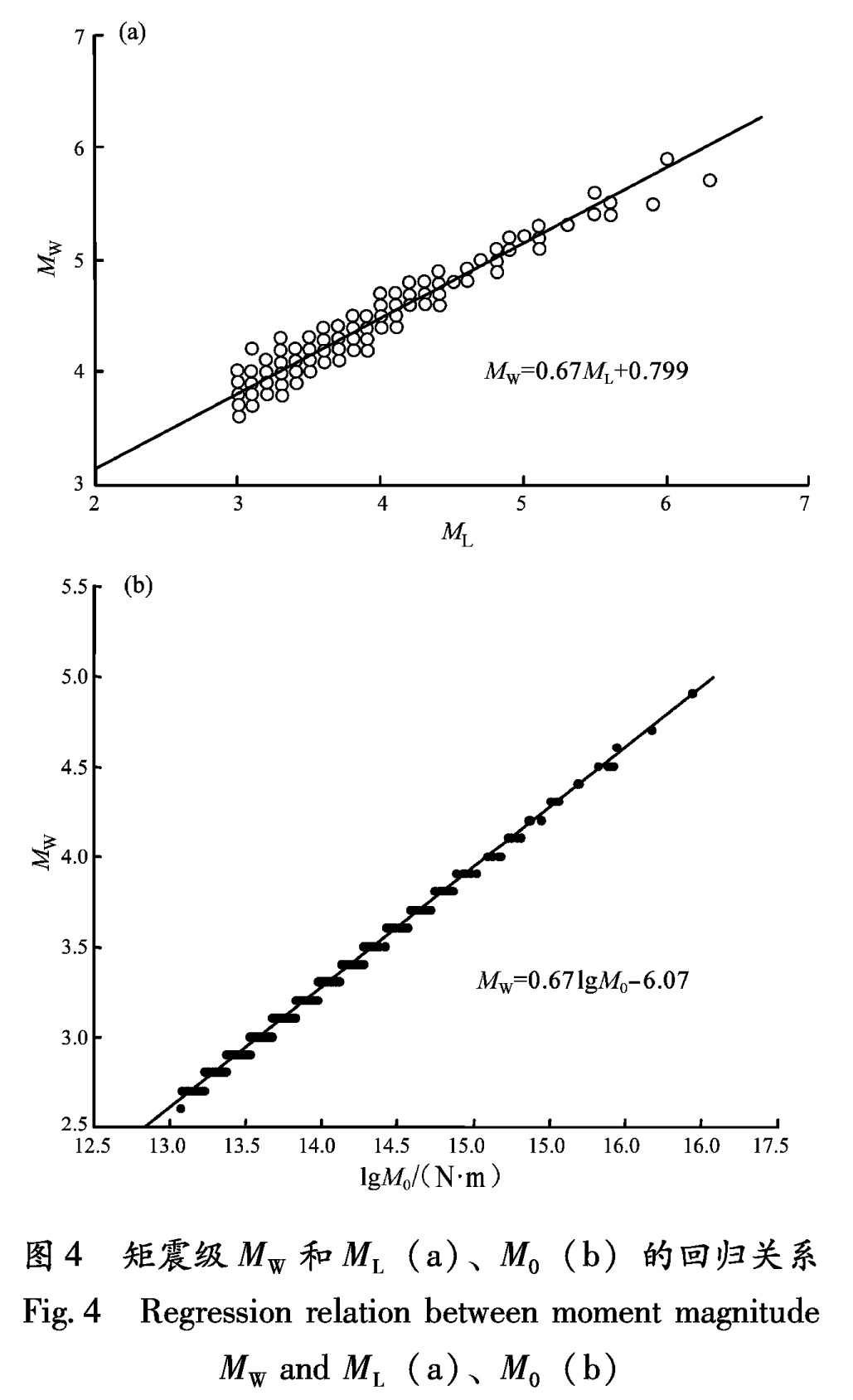
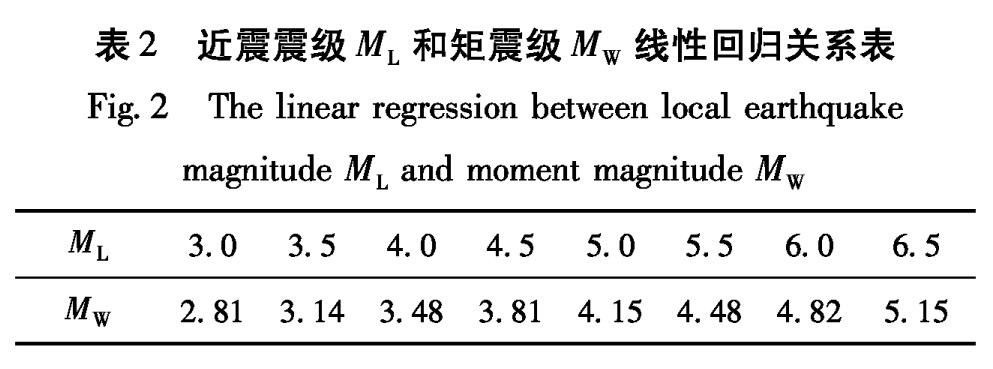
Tab.1 Moment magnitude catalog of ML≥4.0 earthquakes

图4 矩震级MW和ML(a)、M0(b)的回归关系<br/>Fig.4 Regression relation between moment magnitude

图4 矩震级MW和ML(a)、M0(b)的回归关系
Fig.4 Regression relation between moment magnitude

表2 近震震级ML和矩震级MW线性回归关系表<br/>Fig.2 The linear regression between local earthquake magnitude ML and moment magnitude MW

表2 近震震级ML和矩震级MW线性回归关系表
Fig.2 The linear regression between local earthquake magnitude ML and moment magnitude MW

陈运泰,刘瑞丰.2004.地震的震级[J].地震地磁观测与研究,25(6):1-11.
高景春,赵英萍,徐志国,等.2011.河北省测震台网中小地震矩震级的测定[J].华北地震科学,29(2):1-4.
黄玉龙,郑斯华,刘杰,等.2003.华南地区地震波衰减和场地响应的研究[J].地球物理学报,46(1):54-61.
刘丽芳,苏有锦,刘杰,等.2010.云南和四川中小地震应力降时空特征研究[J].地震研究,33(3):314-319.
杨晶琼,杨周胜,刘丽芳,等.2010.2008年盈江5.9级地震序列震源参数研究[J].地震研究,33(4):309-310.
Atkinson G M,Mereu R F.1992.The shape of ground motion attenuation curves in southeastern Canada[J].BSSA,82(5):2 014-2 031.
Brune J N.1970.Tectonic stress and the spectra of seismic shear waves from earthquake[J].JGR,75(26):4 997-5 009.
Hanks T C,Kanamori H.1979.Amomentmagnitudescale[J].JGR,84(B5):2 348-2 350.
Kanamori H.1977.The energy release in great earthquakes[J].JGR,82(20):2 981-2 987.
Moya C A,Aguirre J,Irikura K.2000.Inversion of source parameters and site effects from strong ground motion records using genetic algorithms[J].BSSA,90(4):977-992.
Richter CF.1935.An instrumental earthquake maginitnde scale[J]. BSSA,25(1):1-32.