基金项目:中国地震局地震科技星火计划项目(XH14007Y)和中国地震局2013年度震情跟踪青年课题(2013020204)共同资助.
(1.河北省地震局,河北 石家庄 050021; 2.宽城地震台,河北 宽城 067000; 3.保定中心台,河北 保定 071051; 4.张家口中心台,河北 张家口 075000)
(1.Earthquake Administration of Hebei Province,Shijiazhuang 050021,Hebei,China)(2.Kuancheng Seismological Station,Kuancheng 067000,Hebei,China)(3.Central Seismological Station of Baoding,Baoding 071051,Hebei,China)(4.Central Seismological Station of Zhang
备注
基金项目:中国地震局地震科技星火计划项目(XH14007Y)和中国地震局2013年度震情跟踪青年课题(2013020204)共同资助.
在对比分析地表集中荷载模型和三维有限线段荷载模型的基础上,结合张家口台钻孔体应变2012年1~5月短期异常变化时段受工程影响的实例,采用三维有限线段荷载模型定量计算清水河清淤和蓄水阶段对张家口体应变影响的理论值。结果 表明:计算得到的张家口体应变理论值为-3.12×10-9、4.07×10-9,而实际扣除线性漂移后短期异常为-1.58×10-7、2.30×10-7,理论值远小于实测应变值,因此该项异常变化不能仅归结为工程建设造成的荷载变化所引起,可能存在其他干扰因素或地壳应变变化的共同作用。荷载对钻孔应变观测影响的定量计算,在钻孔应变资料异常分析判定中能起到一定的辅助作用。
On the basis of contrasting the surface concentrated load model and 3D finite line load model,combing with examples of short-term abnormal variation of borehole body strain recorded by Zhangjiakou Station from Jan. to May.,2012,we quantitatively calculate theoretical value of the borehole strain influenced by dredging and water storage of the Qingshui River by use of 3D finite line load model. The results show that the theoretical body strain are -3.12×10-9 and 4.07×10-9,but the short-term abnormal of body strain is -1.58×10-7 and 2.30×10-7 by removing linear drift,which means the theoretical strain value are far less than the actual measured values. Therefore the variation abnormal is not only caused by load fluctuation of engineering construction,but also by other confounding factors or crustal strain changes. Consequently quantitative calculating the influence of load on borehole strain,which can play an additional role in analyzing and determining abnormal borehole strain data.
引言
钻孔应变仪器探头一般安装于钻孔下数十米的基岩中,通过对地层内部应变状态随时间连续变化的精细观测,能捕捉到地壳应力应变微小变化(李海亮,李宏,2010)。钻孔应变能够实时获得区域应变场的连续、低频的钻孔应变资料,由近源地震和地震应力扰动引起的弹性和塑性应变偏移,以及钻孔完成后借助应变仪可获得绝对剪应力状态等(牛安福等,2011)。与地表布设的应变仪器(例如伸缩仪)相比,钻孔应变可以有效地减小地表环境的干扰,但由于钻孔应变观测仪器的分辨力已经达到10-9~10-10,一些环境因素如气压、降雨、气温等仍会对其产生明显干扰,可通过与地应变同步观测的数据记录,进行对比分析,在一定程度上去除此类干扰(李杰等,2003; 马栋等,2011; 杨婕等,2009; 张凌空,牛安福,2008)。
随着城镇建设,钻孔应变观测不断受到工程建设如水库蓄水、高层建筑修建、厂房建设等影响,这些工程建设造成的干扰从根本上均归结为荷载对钻孔应变的影响; 在荷载对钻孔应变及断层形变观测的影响研究方面,胡卫建等(2002)采用经典的集中力作用于半无限弹性体表面的布辛奈斯克解,对钻孔应变测量中地表荷载变化问题做了定量分析研究; 骆鸣津等(2008)给出了地面负荷对应力应变影响的理论模型、并讨论了地层自重的应力应变及引起的钻孔应变; 邱泽华(2004)针对影响钻孔应变观测的河流、湖泊、仓库和铁路等干扰因素分别建立了二维有限均布荷载模型、三维集中荷载模型和三维有限线段荷载模型; 万登堡等(1994)通过在野外开展水位、测震、水温、地电等多种项目的对比观测,研究了列车荷载作用对地震前兆观测的影响; 李祖宁等(2007)根据半无限体表面受法向集中力作用点荷载叠加的原理,计算了大型集装箱堆场对其附近的厦门天马跨断层短水准形变观测场地南点垂直位移的影响; 朱航等(2010)使用岩土力学分析程序计算了耿达短水准场地内施工对水准点位影响的数值解,并对耿达短水准观测资料在汶川MS8.0地震前后出现的异常进行辨别。
本文根据两种荷载对钻孔应变影响的理论模型(地表集中荷载模型和三维有限线段荷载模型),结合张家口台的钻孔体应变观测受工程建设影响的实例,从荷载方面对钻孔应变观测的影响进行定量计算并加以分析。
1 荷载对钻孔应变观测影响的理论模型
现有钻孔应变的荷载模型主要是建立在半无限弹性介质及均布荷载的基础上,主要有地表集中荷载模型(胡卫建等,2002; 骆鸣津等,2008)和三维有限线段荷载模型(邱泽华,2004)。
1.1 地表集中荷载对钻孔应变影响的理论模型骆鸣津等(2008)根据半无限空间均布荷载模型,利用圆柱坐标调和函数推导出的地面负荷对应力应变影响的理论模型。
假定负荷力垂直作用在半无限平面介质的面上,且介质是各向同性的,以负荷着力点为圆柱坐标系的原点,向下为z,水平向外为r。利用满足圆柱坐标的调和函数V(r,θ,z)的解(刘颖,1983)、傅里叶—贝塞尔积分(梁昆淼,1978),可以推出荷载对钻孔产生的平面应变:
err(r,z)=P/(4πu)[(λ+2μ)/(λ+μ)z/((r2+z2)2/3)-(3z2)/((r2+z2)5/2)]+P/(4πμr2)[-μ/(λ+μ)+(λ+2μ)/(λ+μ)z/((r2+z2)1/2)-(z3)/((r2+z2)3/2)],(1)
ezz(r,z)=-P/(4πu)u/(μ(λ+μ))z/((r2+z2)3/2)+P/(4πμ)(3z2)/((r2+z2)5/2),(2)
eθθ(r,z)=P/(4π(λ+μ))1/(r2)-P/(4π)(λ+2μ)/(u(λ+μ))z/(r2)1/((r2+z2)1/2)+P/(4πμ)(z3)/(r2)1/((r2+z2)3/2).(3)
根据err(r,z), ezz(r,z), eθθ(r,z)推演出应力σrr(r,z), σzz(r,z), σθθ(r,z),并用式(4)证明推演的公式是正确的。
σv(r,z)=(3λ+3μ)ev(r,z)=3(λ+2/3μ)ev(r,z)=3kev(r,z).(4)
式中:k为压缩模量,ev(r,z)=err+ezz+eθθ, σv(r,z)=σrr+σzz+σθθ; 式(1)~(4)中P为由于荷载形成的作用于坐标原点并与地面垂直的集中力,r为荷载力作用点至参考点水平投影的距离,z为钻孔深度,λ=(vE)/((1+v)(1-2v)), μ=E/(2(1+v)),E为岩石的弹性模量,v为岩石的泊松系数。根据体应变与面应变的关系(蒋骏,张雁滨,1994),荷载对钻孔体应变的影响为:b=2/3(err(r,z)+eθθ(r,z))。
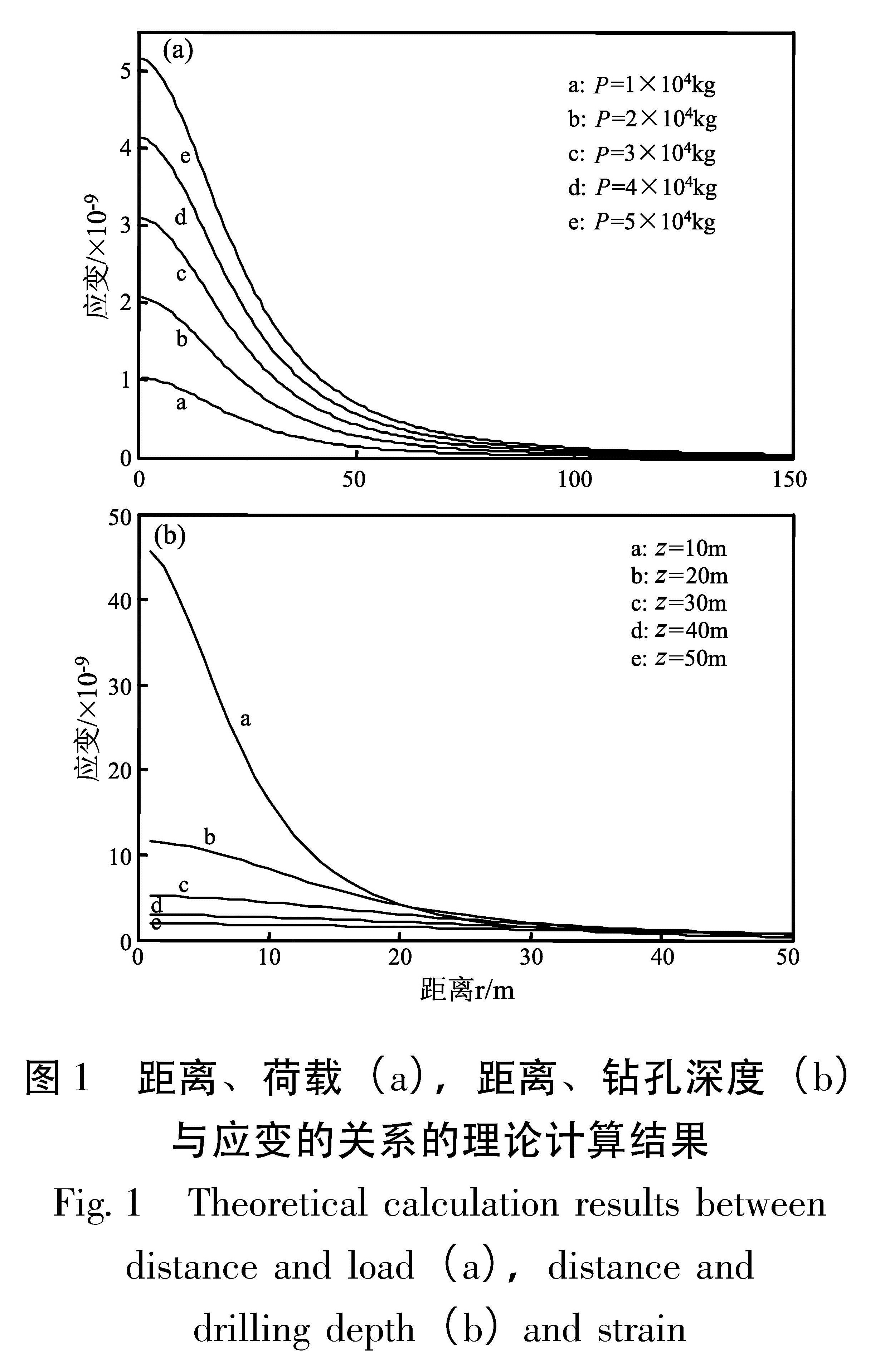
根据骆鸣津等(2008)提出的荷载计算模型,图1a给出钻孔深度z为30 m,荷载分别为P=1×104、2×104、 … …、 5×104 kg的条件下,荷载造成的体应变与荷载距离之间的关系曲线。图1b给出地表荷载P=5×104 kg,钻孔深度z分别为10、20、 … … 、50 m的条件下,荷载造成的体应变与荷载距离之间的关系曲线(计算中岩石弹性模量E=2×1010 Pa、泊松比v=0.35)。
1.2 三维有限线段荷载模型邱泽华(2004)利用集中荷载公式推导出三维有限线段荷载模型。
有限线段荷载上的任一点上的荷载对钻孔应变观测影响的应变值为
ex=-(3Fx2z)/(4μπA5/2)+(Fz)/(4πμA3/2)+(Fx2)/(4πA(z+A1/2)2(μ+λ))+(Fx2)/(4πA3/2(z+A1/2)(μ+λ))-F/(4πA1/2(z+A1/2)(μ+λ)).(5)
式中:λ=(vE)/((1+v)(1-2v)), μ=E/(2(1+v)), F为单位长度的荷载, A=x2+(y-y0)2+z2,以线段荷载的中点为坐标原点,线段荷载中点至钻孔应变探头为x轴方向,线段荷载中点至线段端点为y轴方向,在长为2a的线段上对所有点的影响进行积分,总应变为ext=∫a∫-aexdy0。
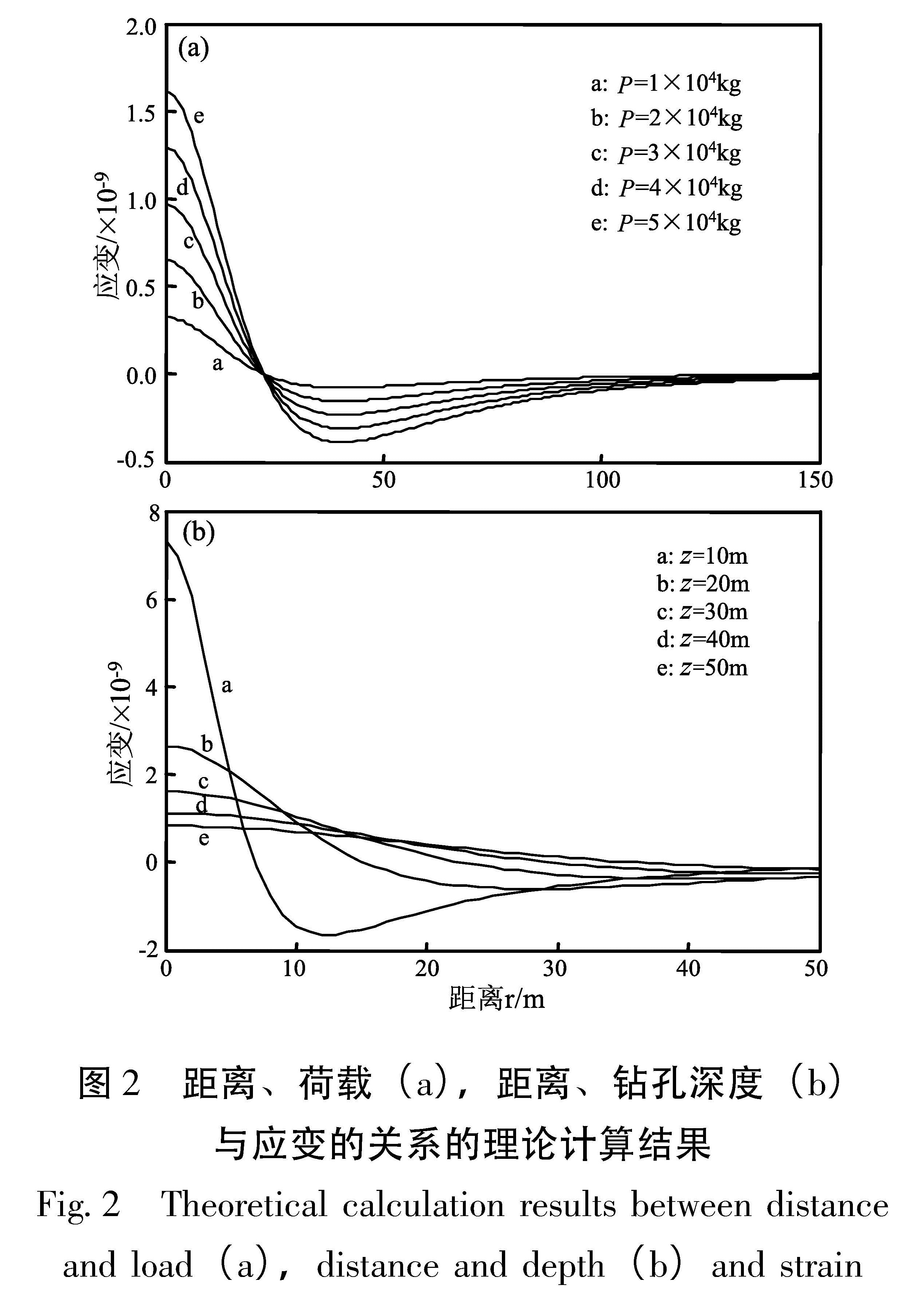
根据邱泽华(2004)提出的有限线段模型,图2a给出钻孔深度z为30 m,荷载分别为P=1×104、2×104 、……、 5×104 kg的条件下,荷载造成的应变与荷载距离之间的关系曲线。图2b给出地表荷载P=5×104 kg,钻孔深度z分别为10、20、… …、 50 m的条件下,荷载造成的应变与荷载距离之间的关系曲线(计算中岩石弹性模量E=2×1010 Pa、泊松比v=0.35)。
由图1、2可以看出,给定钻孔深度(z=30 m)条件下,两种计算模型在距离r<30 m时,差异较大,在r≥30 m时理论计算结果较为接近; 整体来看,集中荷载模型(图1a)较有限线段荷载模型的计算结果(图2a)偏大。图2 距离、荷载(a),距离、钻孔深度(b)与应变的关系的理论计算结果
Fig.2 Theoretical calculation results between distance and load(a),distance and depth(b)and strain给定地表荷载条件下(P=5×104 kg),两种计算模型在距离r<10 m时差异较大,在r≥10m时理论计算结果较为接近; 整体来看,集中荷载模型(图1b)较有限线段荷载模型的计算结果(图2b)偏大。
2 荷载对地应变观测影响的实例分析
2.1 台站地质构造及仪器测项情况张家口地震台处在阴山东西向构造带与山西地震带北段、张渤地震带西北段的交汇部位,附近的主要断裂带为张家口断裂带,该断裂带是北西向张家口—渤海—蓬莱活动构造带西端的一条主要活动断裂,张家口断裂位于宣化—张家口盆地北缘,西自万全城北的水关台,往SE经新平、永丰堡,可能穿过张家口市区北郊,止于清边口一带,走向为NW,倾向为NE,倾角为60°左右,全长约30 km,属正断倾滑型(徐锡伟等,2002)。
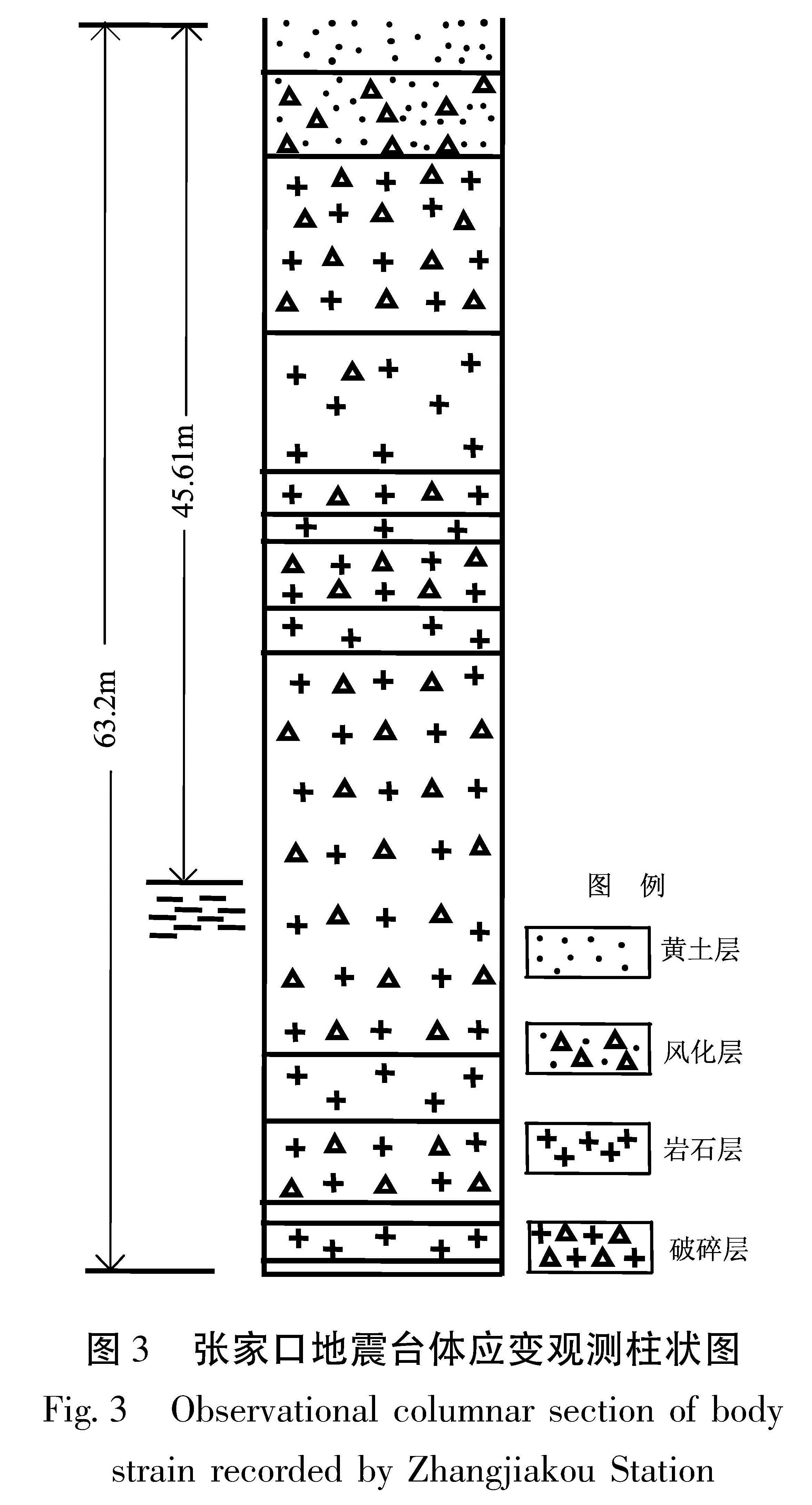
张家口地震台形变观测位于张家口市桥东区鱼儿山山脚,主要测项有DSQ水管倾斜仪、SSY型伸缩仪、VS型垂直摆倾斜仪、SQ-70型石英摆倾斜仪、TJ-2型钻孔体应变仪、GPS连续观测(陆态网GNSS基准站),是观测项目较为齐全的综合形变观测台站。张家口台钻孔体应变仪于1989年5月安装,孔深63.2 m,钻孔直径220 mm,年稳定性4.0×l0-8。井孔位于侏罗纪火山岩中,岩性为片麻岩,井水为基岩裂隙水,与地表潜水不相通,水温约11 ℃,探头水下埋深约20 m,辅助观测主要有气压、水位、孔温等(池海江等,2005),张家口体应变观测井柱状图见图3。
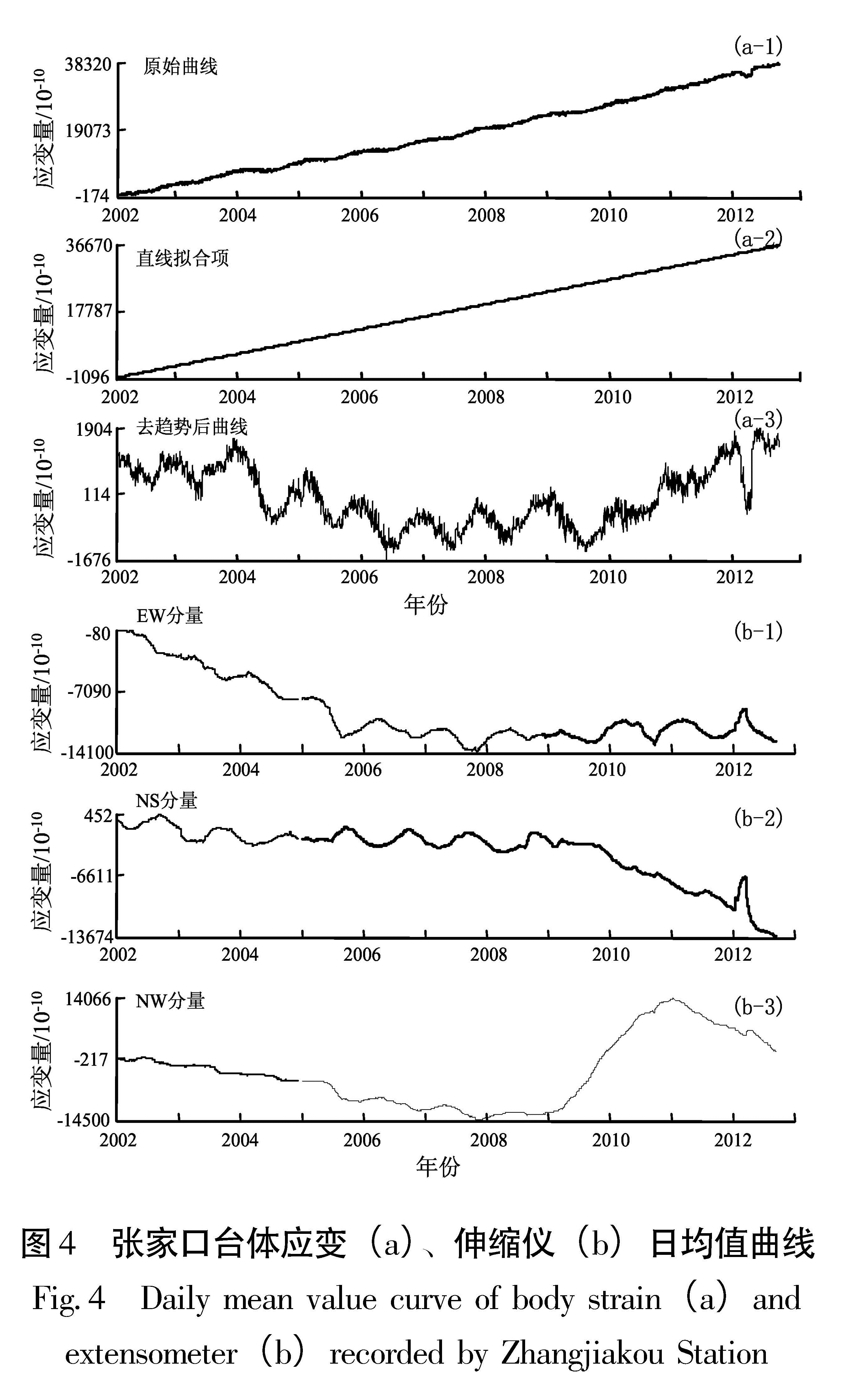
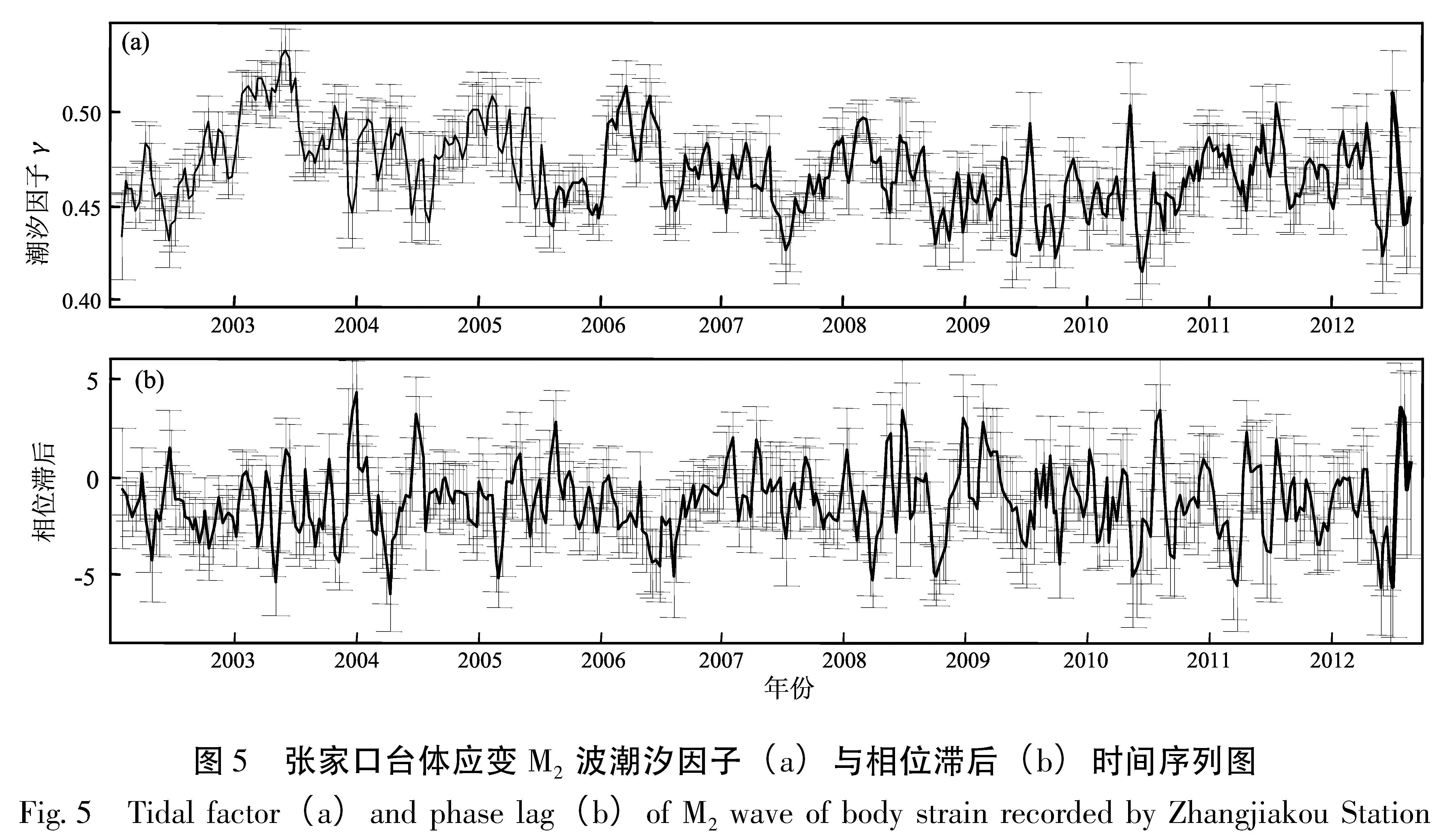
2.2 张家口钻孔体应变荷载影响分析张家口钻孔体应变与伸缩仪2012年1~5月出现非常明显的同步短期变化,表现为在原有背景上由张性转为压性的变化过程,变化幅度分别为:体应变的张性和压性变化量已分别达到1.58×10-7、2.30×10-7(通过直线拟合扣除线性漂移后)、伸缩仪EW分量0.9×10-7、NS分量6.4×10-7、NW分量1.1×10-7(图4),且倾斜类仪器如水管仪、垂直摆等在此期间也出现同步短期变化情况。根据应变资料质量评价方法(马栋等,2013),对张家口体应变观测数据(小时值)用Venedikov调和分析方法(30天窗长,10天步长滑动)计算M2波潮汐因子和相位滞后,并给出计算误差,根据计算结果对资料的稳定性进行定量评价(图5),潮汐因子变化范围为0.414 9~0.533 3,计算误差范围为0.007 6~0.037 7; 相位滞后变化范围为-5.982 2~4.345 3,计算误差范围为0.847 2~4.757 3,因此2002~2012年张家口体应变M2波潮汐因子和相位滞后都非常稳定,该时段仪器观测系统工作正常。同一台站地应变、地倾斜测项都出现明显的同步短期变化,根据以往的震例研究分析,这种集中同步的短期变化很可能是由一些干扰因素造成的,也可能是局部地壳应力的变化所致; 虽然变化时间不完全一致,
可能是各种仪器对应力积累或干扰的反映不同而造成时间上的延迟。所以有必要对此短期变化从台站周围的环境变化等方面做详细的调研和分析论证工作,为异常分析判定提供可行的方法和依据。图3 张家口地震台体应变观测柱状图
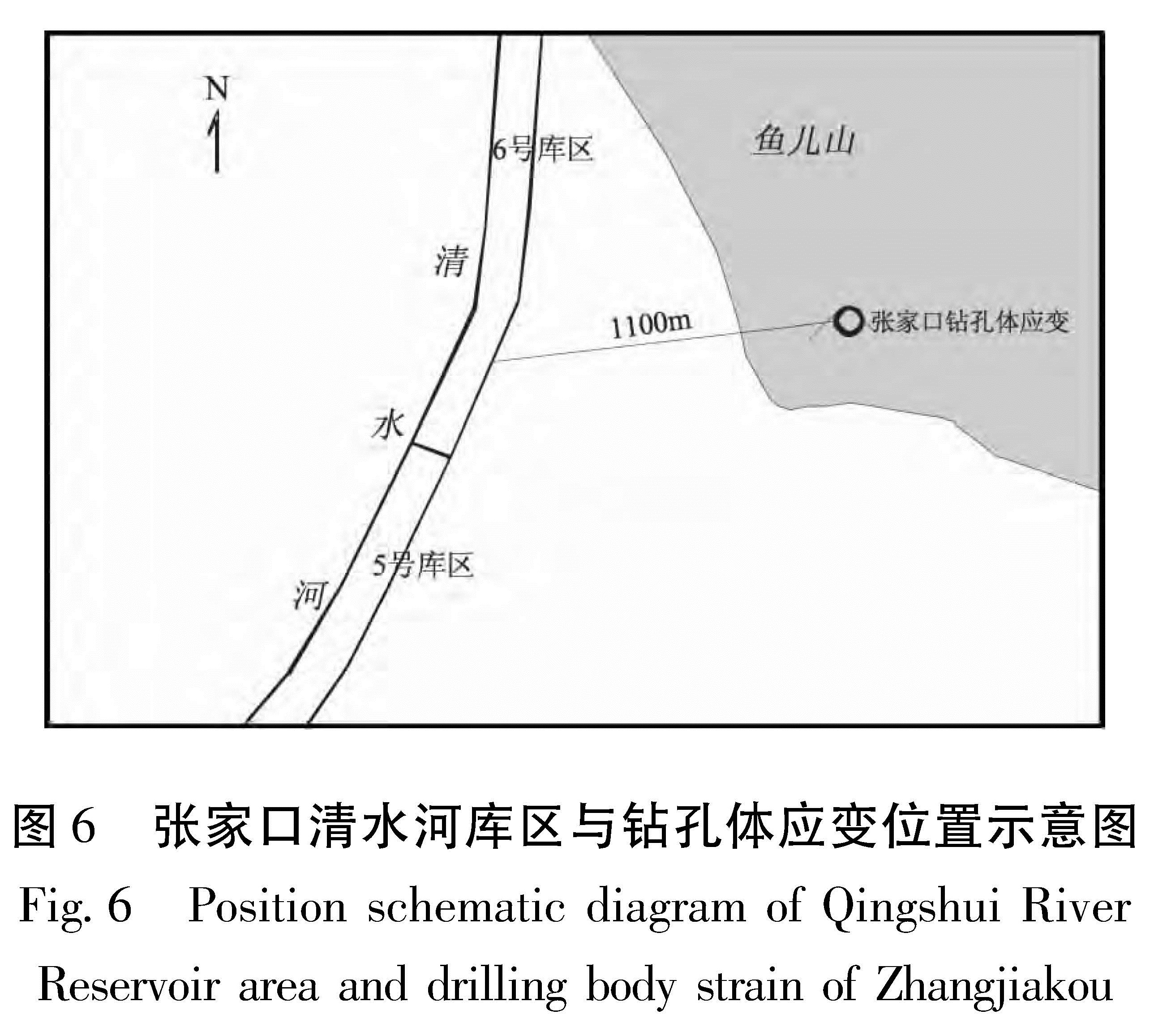
Fig.3 Observational columnar section of body strain recorded by Zhangjiakou Station经过实地异常落实,在此短期异常变化时段,张家口台站周围明显的环境变化仅有张家口市清水河清淤和蓄水工程。清水河清淤、蓄水河段距张家口钻孔体应变1 100 m,施工河段分为5号、6号库区,5号库区坝长123 m,河道长510 m,坝高2.7 m; 6号库区坝长107 m,河道长465 m,坝高3.5 m(图6)。清淤工程2012年2月28日开始,先将清淤河段0.6 m深的少量存水放到下游,于3月20日进行大规模清淤施工,3月30日5号库区清淤结束,4月8日6号库区清淤结束,清淤总量1.54×105 m3。清淤后,4月12日开始蓄水,流量1 m3/s,5月1日蓄水结束,5号和6号库区蓄水总量3.016×105 m3(据张家口市清水河河道管理处)。
图4 张家口台体应变(a)、伸缩仪(b)日均值曲线
Fig.4 Daily mean value curve of body strain(a)and extensometer(b)recorded by Zhangjiakou Station图5 张家口台体应变M2波潮汐因子(a)与相位滞后(b)时间序列图
Fig.5 Tidal factor(a)and phase lag(b)of M2 wave of body strain recorded by Zhangjiakou Station3 荷载影响的模型及计算分析
由于清水河清淤和蓄水的河道较为平直,荷载变化可以近似为线性荷载,因此采用三维有限线段荷载模型(邱泽华,2004)计算更为合理; 为定量分析河道清淤和蓄水造成的荷载变化对张家口钻孔体应变观测的影响,根据三维有限线段荷载模型,从理论上计算荷载变化引起的张家口体应变的应变变化。荷载计算的各项参数如下:清淤造成的荷载减少量:P1=15.4×107×1.5=2.31×108 kg(取淤泥的密度为1.5×103/m3); 蓄水造成的荷载增加量:P2=3.02×108 kg; 清水河至体应变观测井的水平距离r=1.1×103 m; 张家口体应变探头深度为60 m,从体应变井口至清水河的高差约为20 m,因此取深度z=60-20=40 m。张家口体应变钻孔岩性为片麻岩,取岩石弹性模量E=4×1010 Pa、泊松比v=0.25(苏恺之,1985)。
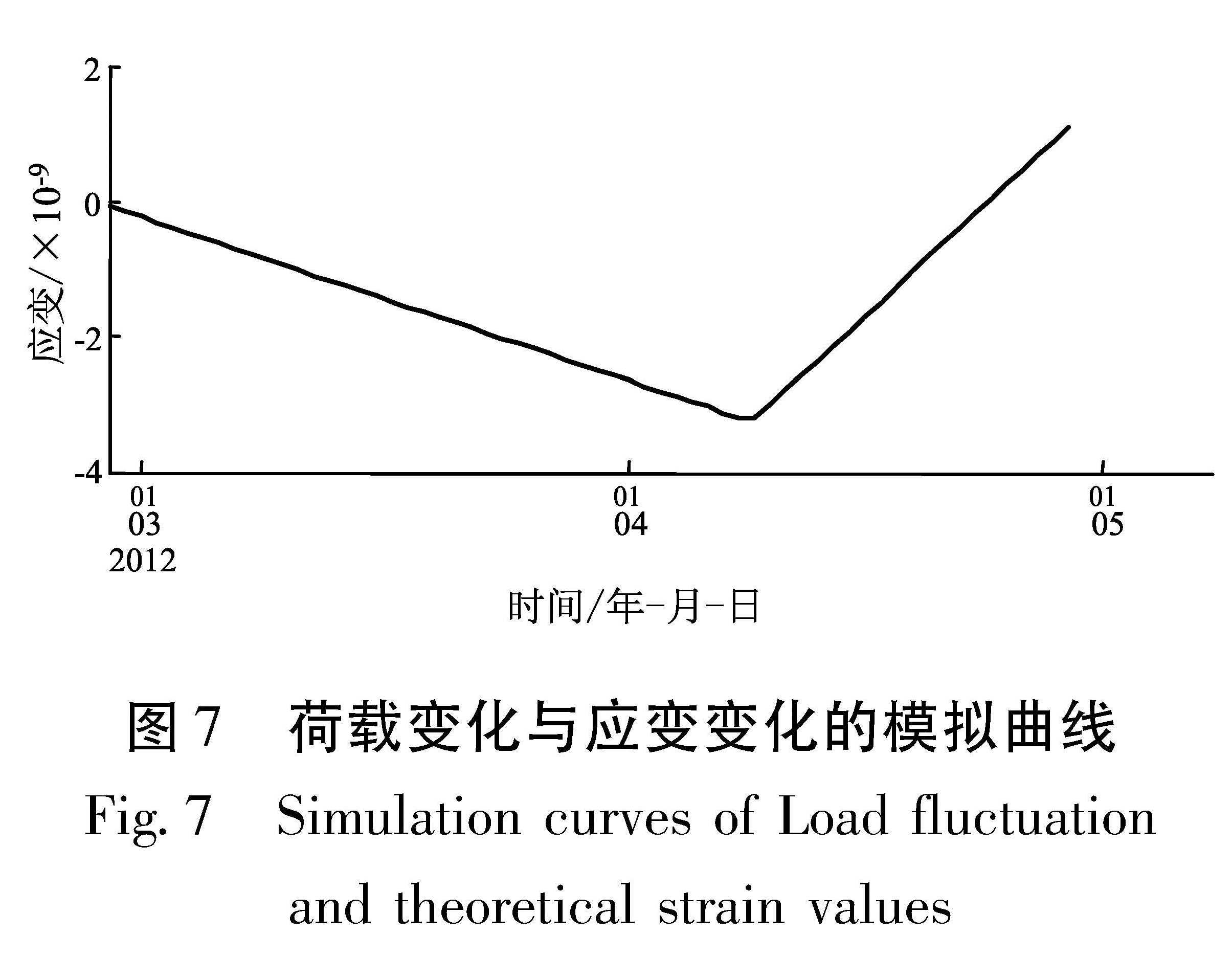
由于未能获取张家口清水河清淤和蓄水阶段每日的荷载变化量,因此简化为清淤阶段的每日的荷载变化量为:清淤总量(P1=2.31×108 kg)/清淤天数(40 d); 蓄水阶段的每日的荷载变化量为:蓄水总量(P2=3.02×108 kg)/蓄水天数(19 d); 根据三维有限线段荷载模型(邱泽华,2004),模拟出2013年2~5月张家口清水河清淤和蓄水阶段的荷载变化与张家口体应变的应变变化理论值的曲线(图7),模拟曲线与同时段张家口体应变的观测曲线的形态有一定的关联,但是模拟值较实际观测的应变值偏小2~3个数量级。
按照总的清淤量和蓄水量来计算,清水河清淤阶段荷载引起的应变为-3.12×10-9,蓄水阶段荷载引起的应变为4.07×10-9(表1); 2012年1~5月,张家口体应变在扣除线性漂移后的张性和压性变化量已分别达到1.58×10-7、2.30×10-7,根据荷载理论模型计算出的应变量远小于实际应变量,因此认为2012年1~5月张家口体应变的短期异常变化不能仅归结为清水河清淤和蓄水所造成,可能存在其他因素或地壳应变变化的共同作用。4 结论
荷载对钻孔应变观测的影响在实际的资料分析中需要定性与定量分析相结合,定性分析主要是从时间进程上判定荷载对地应变产生的影响,总体来说具有较高的准确性,但不能确定荷载所引起的应变的量值。通过建立理论模型定量分析荷载对应变观测的影响可以初步给出定量的结果,但是该方法在荷载距离应变观测较近、或者荷载变化量较大时才较为有效,因为地壳结构复杂,假定的模型是建立在各向同性弹性体的空间应力状态下的,距离越远或者荷载变化量越小则模型的准确性越差。
根据荷载对钻孔应变影响的理论模型计算结果,清水河清淤和蓄水对张家口体应变造成的影响的理论计算值远低于实际体应变资料的变化,因此初步认为张家口钻孔体应变2012年1~5月的短期异常变化不能归结为清水河清淤和蓄水造成的荷载变化引起,可能存在其他干扰因素或地壳应变变化的共同作用。
已有的荷载计算钻孔体应变影响的模型只考虑地壳为均一介质,而实际钻孔位置的地壳结构存在明显的分层,进一步的工作需要采用数值模拟等方法进行分析。
在异常分析及资料收集中得到了张家口中心台和张家口清水河河道管理处的帮助,在此表示衷心感谢。
- 池海江,朱振兴,王锐锋,等.2005.张家口台印尼苏门答腊大地震钻孔应变观测报告[J].地壳构造与地壳应力,(2):4-8.
- 胡卫建,张俊山,谢智,等.2002.荷载对钻孔应变测值影响的实验及力学解析[J].地震,22(3):95-104.
- 蒋骏,张雁滨.1994.潮汐线应变组合观测的物理力学实质及其调和分析[J].地球物理学报,37(S2):204-212.
- 李海亮,李宏.2010.钻孔应变观测现状与展望[J].地质学报,84(6):895-900.
- 李杰,刘敏,邹钟毅,等.2003.数字化钻孔体应变干扰机理及异常分析[J].地震研究,26(3):230-238.
- 李祖宁,吴绍祖,陈光,等.2007.利用点荷载叠加方法研究天马跨断层短水准异常资料[J].地震研究,30(1):35-38.
- 梁昆淼.1978.数学物理方法[M].北京:人民教育出版社,371.
- 刘颖.1983.圆柱函数[M].北京:国防工业出版社,66.
- 骆鸣津,池顺良,马鸿钧.2008.地层绝对应力测量与钻孔应变测量[M].北京:地震出版社,170-177.
- 马栋,牛安福,袁淑芳,等.2011.据频谱特征分析短时气压波动对体应变的影响[J].内陆地震,25(3):255-262.
- 马栋,晏锐,武艳强,等.2013.张渤带洞体应变参数解算及结果分析[J].中国地震,29(1):99-107.
- 牛安福,张凌空,闫伟,等.2011.中国钻孔应变观测能力及在地震预报中的应用[J].大地测量与地球动力学,31(2):48-52.
- 邱泽华.2004.钻孔应变观测点到地面载荷干扰源最小“安静” 距离的理论分析[J].岩石力学与工程学报,23(23):4 063-4 067.
- 苏恺之.1985.地应力测量方法[M].北京:地震出版社,192-193.
- 万登堡,王家彬,刘国寿.1994.列车荷载作用对某些前兆观测的影响[J].地震,(6):91-94.
- 徐锡伟,吴卫民,张先康.2002.首都圈地区地壳最新构造变动与地震[M].北京:科学出版社.
- 杨婕,占惠,凌学才.2009.强降水对厦门地震台伸缩仪的影响[J].大地测量与地球动力学,29(增刊):76-78.
- 张凌空,牛安福.2008.不同周期气压波对钻孔体应变仪观测结果的影响[J].中国地震,24(4):415-421.
- 朱航,苏琴,杨涛,等.2010.耿达短水准观测资料在汶川MS8.0地震前后异常的辨别[J].地震学报,32(6):649-658.