基金项目:江苏省地震局青年科学基金项目(201302)资助.
(Earthquake Administration of Jiangsu Province,Nanjing 210014,Jiangsu,China)
situ stress; borehole strain; coupling coefficient; drilling model; stress field
备注
基金项目:江苏省地震局青年科学基金项目(201302)资助.
利用4层介质耦合钻孔模型,研究该模型中耦合介质弹性参数变化对钻孔应变耦合系数的影响。计算结果表明:在钻孔耦合介质中,弹性层等效弹性模量变化对面应变耦合系数的影响大于对差应变的影响,与观测结果对比,分析发现面应变耦合系数观测值存在明显非均匀性,而且其大小与台站的背景应力场存在对应关系。
Using the established four layer medium coupled drilling model,we calculated the effect of elastic parameters variation of borehole coupling medium on coupling coefficients of borehole strain by stress function method. The calculation results show that the effect of equivalent elastic modulus change on the coupling coefficients of the plane strain is larger than that of the shear strain in the borehole coupling medium. Comparing with the observed data,the observation value of the coupling coefficients of the plane strain exhibits a significant heterogeneity,as well as its value may relate to the background stress field of the station.
引言
钻孔应变研究中,人们关注的是应变观测曲线的相对变化,可以利用厚壁筒力学模型给出地层应力与钻孔应变之间的耦合关系,将观测的应变变化转化成应力变化进行分析研究(潘立宙,1981; Gladwin,Hart,1985)。前人对钻孔应变耦合系数的研究方法主要有两种:一是数值模拟方法,利用力学模型分析介质的弹性参数变化对钻孔应力—应变的耦合关系影响:二是潮汐标定方法,利用钻孔力学模型对固体潮潮汐的响应反演耦合介质弹性参数(骆鸣津等,1989; Hart et al.,1996)。采用数值模拟方法进行定量分析(李玉江等,2011; 张凌空,牛安福,2013),受限于模型介质参数的取值,直接用其对观测数据的产生机理进行分析仍存在一定困难。高龙生(1973)分析认为钻孔固结介质与围岩之间存在的非完全耦合会对观测结果产生影响,邱泽华等(2005)利用潮汐标定对实际观测结果进行分析后,认为钻孔耦合状态与围岩介质的非均匀性存在关联; Langbein等(2010)和Hodgkinson(2013)对同一台站多套形变仪器测量结果对比分析后认为潮汐力大小不可忽视。另外还存在一些认识,池顺良等(2007)进行数值模拟与观测结果对比分析,认为断层阻隔了潮汐应力的传递,Roeloffs(2010)等研究认为局部地层的垂向应变对钻孔应变观测产生影响,张晶和刘琦(2012)分析认为差应变潮汐相位滞后与地下介质各向异性存在关联。
综上所述,在钻孔应力—应变耦合关系分析中,如何能准确的解读出观测数据中所反映的信息,取决于研究人员对观测数据产出机理的理解。笔者在分析野外实验数据后,发现实际观测中钻孔围岩与真实地层的弹性模量之间竟然相差1~2个量级,钻孔岩体围岩弹性模量测值在(0.1~6.5)GPa范围内(艾凯等,2003),而地层的弹性模量测值在(1.0~7.0)GPa范围内(秦向辉等,2012),分析认为该现象与原地应力对钻孔围岩卸载作用存在关联,在研究耦合介质弹性参数变化对钻孔耦合系数影响时不可忽视。本文给出了“探头—水泥环—弹性层—地层”4层介质组合模型,并进行了数值模拟分析、与实际观测数据对比分析,验证了4层组合模型的有效性和合理性。
1 钻孔物理模型及耦合系数表达式
根据地层受非均匀地层应力作用的特点,将其分解为与方位角无关的面应力项以及与方位角有关的偏应力项,并将问题转化成两个平面应力状态下的弹性力学问题,再分别分析地层在面应力和偏应力作用下的应力场和位移场,最后由叠加原理获得地层中应力场和位移场。
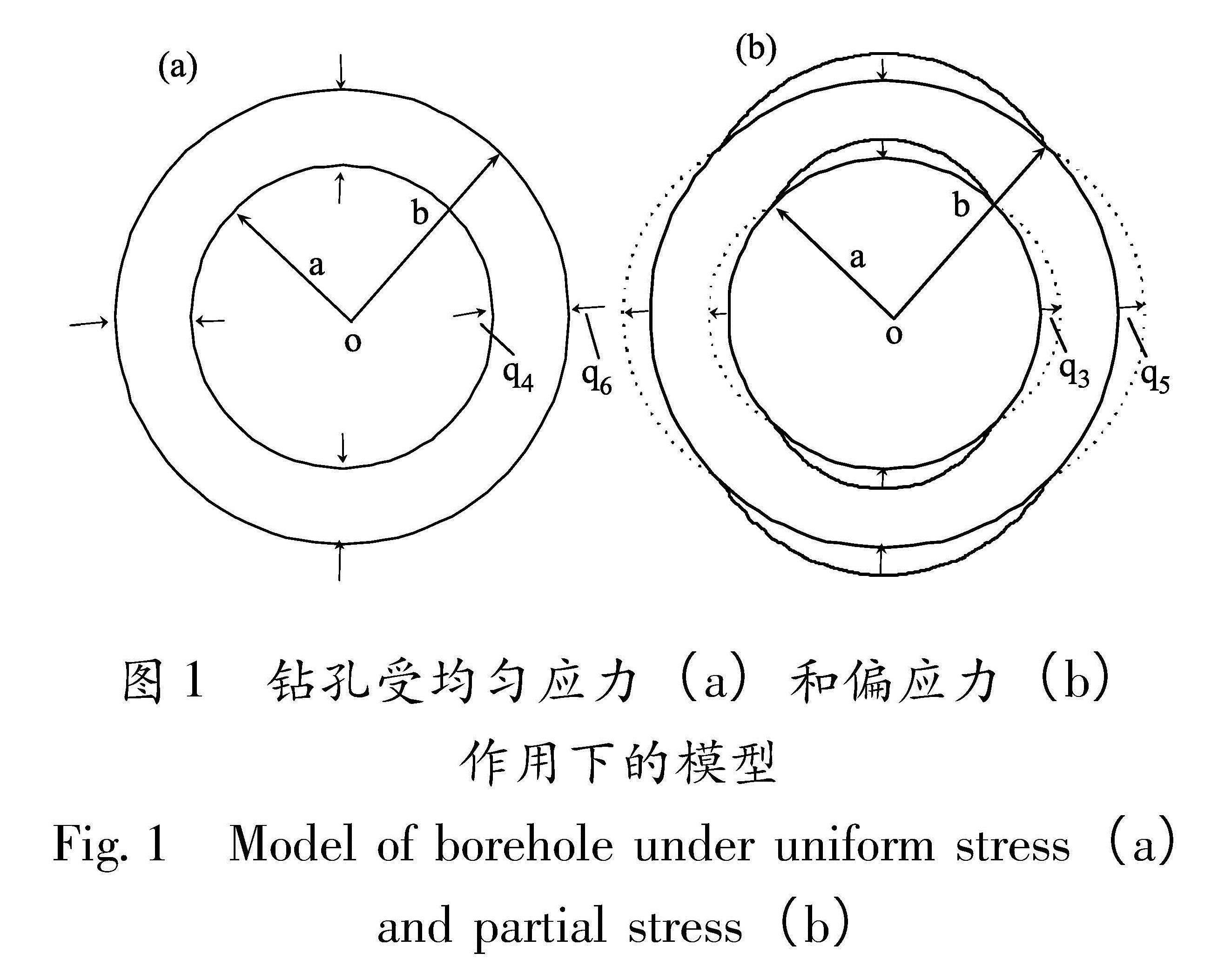
1.1 空孔模型及耦合系数计算无限大地层带有半径为a的圆孔在非均匀地应力q1和q2作用下,可分解为面应力q和偏应力s的组合表达式:
q=(q1×q2)/2,s=(q1-q2)/2.(1)
地层中空孔的受力问题可分解成两个平面应力问题,均匀应力q作用下的力学模型(图1a)和偏应力s作用下的受力模型(图1b),再将两个平面问题进行叠加,可获得地层中空孔的应力场和位移场。
依据弹性力学中的极坐标下平面问题,采用应力函数法进行求解,可得平面应力状态下地层的应力函数表达式(徐芝纶,2006)为{σρ=A/(ρ2)+2C-(2B'+(4C')/(ρ2)+(6D')/(ρ4))cos2θ,
σθ=-A/(ρ2)+2C+(12A'ρ2+2B'+(6D')/(ρ4))cos2θ,
τρθ=(6A'ρ2+2B'-(2C')/(ρ2)-(6D')/(ρ'))sin2θ.(2)
式(2)中,A、B、A'、B'、C'、D'为待定系数,当b>>a时,满足应力边界条件
〖JB<4{〗(σρ)ρ=a=0,(τ'ρθ)ρ=a=0,
(σρ)ρ=b=q+scos2θ,(τρθ)ρ=b=-ssin2θ.(3)
假设E和v分别表示地层弹性模量和泊松比,由几何方程和物理方程可得地层位移表达式为
{uρ=1/E{2(1-v)Cρ-(1+v)A/ρ-[4vA'ρ3
+(1+v)2B'ρ-(4C')/ρ-(1+v)(2D')/(ρ3)]cos2θ},
uθ=1/E[(6+2v)A'ρ3+(1+v)2B'ρ+(v-1)
(2C')/ρ+(1+v)(2D')/(ρ3)]sin2θ.(4)
对无孔地层,在ρ=a和ρ=b处应力相同,由式(2)、(3)、(4)可得任一点应变eρ表达式为
eρ=(uρ=a)/a=(1-v)/Eq+(1+v)/Escos2θ,(5)
假设R和S分别表示面应变耦合系数和差应变耦合系数,在ρ=a处,钻孔径向应变eρ可表示为面应变和差应变的组合函数:
eρ=(uρ=a)/a=R(1-v)/Eq+S(1+v)/Escos2θ
=R(ε1+ε2)/2+S(ε1-ε2)/2cos2θ,(6)
对空孔条件,由式(2)~(4)可得在ρ=a处应变eρ表达式为
eρ=(uρ=a)/a=2/Eq+4/Escos2θ.(7)
由式(6)可得空孔时,钻孔应变的耦合系数R、S分别为
R=2/(1-v)=2.667, S=4/(1+v)=3.2 .(8)
1.2 n层介质耦合钻孔模型及耦合系数计算在平面应力条件下,对n层均匀各向同性介质组合模型,取i =1~n,第i层的内外半径分别为ri 和ri+1,利用式(2)、(3)可得该层介质中应力表达式为
{σρ=(Ai)/(ρ2)+2Ci-(2B'i+(4C'i)/(ρ2)+(6D'i)/(ρ4))cos2θ,
σθ=(Ai)/(ρ2)+2Ci+(12A'iρ2+2B'i+(6D'i)/(ρ4))cos2θ,
τρθ=(6A'iρ2+2B'i-(2C'i)/(ρ2)-(6D'i)/(ρ4))sin2θ.(9)
由几何方程和物理方程可得第i层介质中位移表达式为
{uρ=1/E{2(1-vi)Ciρ-(1+vi)(Ai)/ρ-[4viA'iρ3
+2(1+vi)B'iρ-(4C'i)/ρ-(1+vi)(2D'i)/(ρ3)]cos2θ},
uθ=1/E[(6+2vi)A'iρ3+2(1+vi)B'iρ+(vi-1)
(2C'i)/ρ+(1+vi)(2D'i)/(ρ3)]sin2θ.
(10)
该n层介质组合模型满足边界条件
〖JB<4{〗(σρ)ρ=r1=0,(τ'ρθ)ρ=r1=0,
(σρ)ρ=ri+1=q+scos2θ,(τρθ)ρ=ri+1=-ssin2θ.(11)
同时两种介质的接触面上, 满足应力连续和位移连续的边界条件:
{σρ=ri+1(θ,Ai,Ci,A'i,B'i,C'i,D'i)
=σρ=ri+1(θ,Ai+1,Ci,A'i+1,B'i+1,C'i+1,D'i+1),
τθρ(θ,ri,Ai,Ci,A'i,B'i,C'i,D'i)
=τθρ(θ,ri+1,Ai+1,Ci+1,A'i+1,B'i+1,C'i+1,D'i+1),
up=ri+1(Ei,vi,θ,Ai,Ci,A'i,B'i,C'i,D'i)
=uρ=ri+1(Ei+1,vi+1,θ,Ai+1,Ci+1,A'i+1,B'i+1,C'i+1,D'i+1),
uθ(Ei,vi,θ,ri,A'i,B'i,C'i,D'i)
=uθ(Ei+1,vi+1,θ,ri+1,A'i+1,B'i+1,C'i+1,D'i+1).
(12)
将式(9)、(10)分别代入式(11)、(12)可得6n个未知参数的6n个线性方程组,该方程组可分解为一个与面应力q有关的2n个未知参数的2n个线性方程组,以及与偏应力s有关的4n个未知参数的4n个线性方程组。利用线性方程组求解的克莱姆法则,可计算各未知参数,将计算后的未知参数代入式(10),则钻孔内径ρ=r1处应变eρ的理论公式为
eρ=(uρ=ri)/(ri)=Mq+Nscos2θ,(13)
式中,M,N是与钻孔模型参数有关的常数。假设Em和νm分别表示地层弹性模量和泊松比,R和S分别表示面应变耦合系数和差应变耦合系数。在ρ=r1处,应变eρ可写成如式(6)的形式:
eρ=(uρ=ri)/(r1)=R(1-vm)/(Em)q+S(1+vm)/(Em)scos2θ
=R(ε1+ε2)/2+S(ε1-ε2)/2cos2θ.(14)
解方程组(13)和(14),可得R和S的理论值分别为(Em)/(1-vm)M和(Em)/(1+vm)N。
1.3 原地应力卸载作用下钻孔模型及耦合系数计算钻孔开挖后,钻孔围岩受原地构造应力σ1和σ2影响,α为原地应力的方位角,受到原地应力作用,钻孔的径向卸载应力Δσρ和切向卸载应力Δσθ表达式(蔡美峰,2011)为
{Δσρ=-(σ1+σ2)/2-(σ1-σ2)/2cos2(θ+a),
Δσθ=-(σ1+σ2)/2-(3(σ1-σ2))/2cos2(θ+a).(15)
在围压较高的岩层中钻孔,钻孔内壁围岩由于围压卸载作用会产生大量微裂隙和层面裂隙,孔壁围岩弹性模量的大小除与岩石性质有关外,还受岩石裂隙密度变化的影响,适用于细观损伤理论Taylor公式(余寿文,冯西桥,1997)为
(E')/E=[1+(16)/(45)((1-v2)(10-3v))/(2-v)f]-1.(16)
式中,E为基体材料弹性模量; E'为含裂纹的基体材料有效弹性模量; ν为基体材料泊松比; f为微裂纹密度。式(16)表明,随着裂纹密度增加,材料有效模量减小。
若钻孔耦合介质存在各向异性非均匀及非中心耦合,都会导致钻孔应变的耦合系数R、S具有方向性,可用近似椭圆的数学模型来拟合(骆鸣津等,2008):
{R(α)=R0+R'cos2(θ+a),
S(α)=S0+S'cos2(θ+a).(17)
式中,R0、R'、S0、S'表示耦合系数的非均匀各向异性参数,在钻孔内径ρ=r1处钻孔应变仍可写成如式(6)的形式:
(u(ρ,θ))/ρ=[R0+R'cos2(θ+a)](ε1+ε2)/2
+[S0+S'cos2(θ+a)](ε1-ε2)/2cos2θ.(18)
在四分量钻孔应变中,可以利用式(18)计算两个相互垂直方向的组合和应变与组合差应变
{(u(ρ,θ))/ρ+(u(ρ,θ+0.5π))/ρ
=R0(ε1+ε2)+S'(ε1-ε2)cos2(θ+a)cos2θ,
(u(ρ,θ))/ρ-(u(ρ,θ+0.5π))/ρ
=R'(ε1+ε2)cos2(θ+a)+S0(ε1-ε2)cos2θ.(19)
由式(19)可以看出,只有在非均匀耦合系数R'、S'均等于0情况下,四分量应变的组合和应变满足“自检条件”。由于受实际观测条件限制,耦合介质很难满足理想的均匀各向同性条件,因此,通过潮汐标定方法计算钻孔耦合系数时,需要考虑介质耦合的非均匀性影响。
2 观测模型改进与耦合系数物理意义
建立“钢筒、水泥环、地层”3层介质钻孔模型,需要知道各层耦合介质的相关参数,测量钢筒的弹性模量和泊松比以及半径大小可由生产厂家提供,水泥的弹性模量和泊松比可由实验室测试提供,钻孔的半径大小可知,野外实验观测数据给出地层的弹性模量在一定范围变化。以RYR-4分量应变的模型参数为例:钢筒材料的弹性模量Es=210 GPa、泊松比νs=0.3,水泥材料弹性模量Ec=(20~35)GPa、泊松比νc=0.25,钢筒内半径r1=51.5 mm、外半径r2=53.5 mm,钻孔的半径r3=65 mm。假设地层弹性模量Em=(10~100)GPa、泊松比νm=0.25,根据以上参数可建立3层各向同性均匀介质钻孔模型(图2a),利用该模型可分析地层弹性模量变化对耦合系数的影响。由于实际观测中存在原地构造应力,钻孔开挖会造成钻孔局部应力重新分布,在钻孔内壁径向载荷消失,孔壁岩石受径向应力卸载影响,围岩弹性性质会发生变化,需要在水泥介质与地层之间增加一个弹性层,对“钢筒、水泥环、地层”3层介质模型进行修正(图2b),该弹性层的等效弹性模量Ee与围岩的孔隙密度相关,4层介质组合的钻孔模型与真实观测条件基本相符。
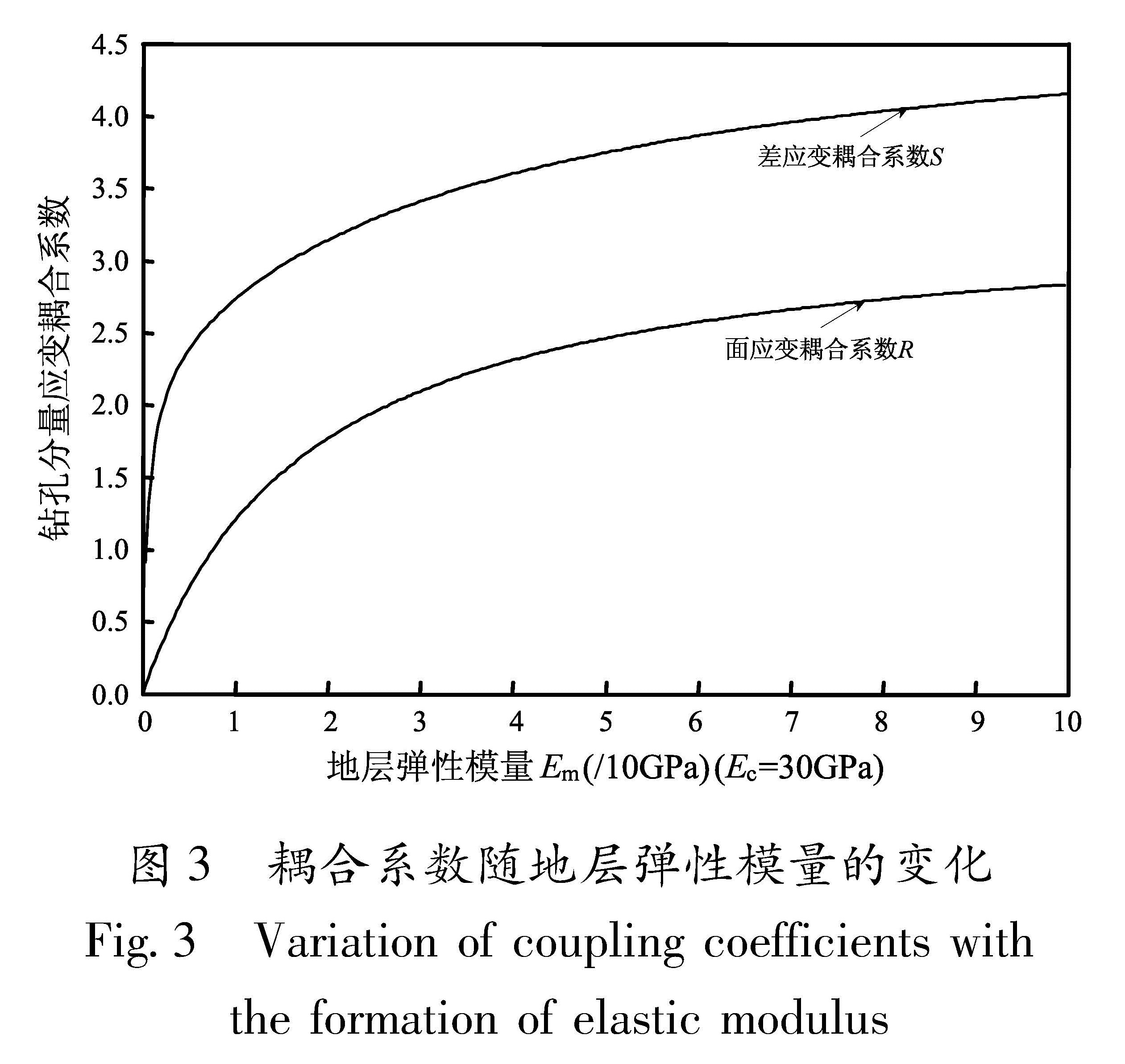
经实验严格配方,其用于固结钢筒与孔壁的水泥弹性模量可控制在(20~40)GPa,假设地层弹性模量Em=(30~70)GPa,钢筒材料的弹性模量和泊松比由生产厂家提供,可以利用3层介质组合模型定量分析地层弹性模量Em变化对耦合系数R、S的影响。取水泥介质弹性模量Ec=30 GPa,图3给出了RYR-4钻孔应变的耦合系数R、S随地层弹性模量Em变化的关系曲线,从图中可以看出耦合系数R和S的大小随地层弹性模量的增加快速增加后趋于变缓,耦合系数S先于R趋于变缓。当地层弹性模量较小时,对面应变耦合系数R影响较大、对差应变耦合系数S影响相对较小; 当地层弹性模量在300 GPa以上,差应变耦合系数S是面应变耦合系数R的1.5倍左右,此时差应变耦合系数S已经大于空孔耦合系数3.2,面应变耦合系数R也大于2,随地层弹性模量的进一步增加,面应变耦合系数R会大于空孔耦合系数2.667。
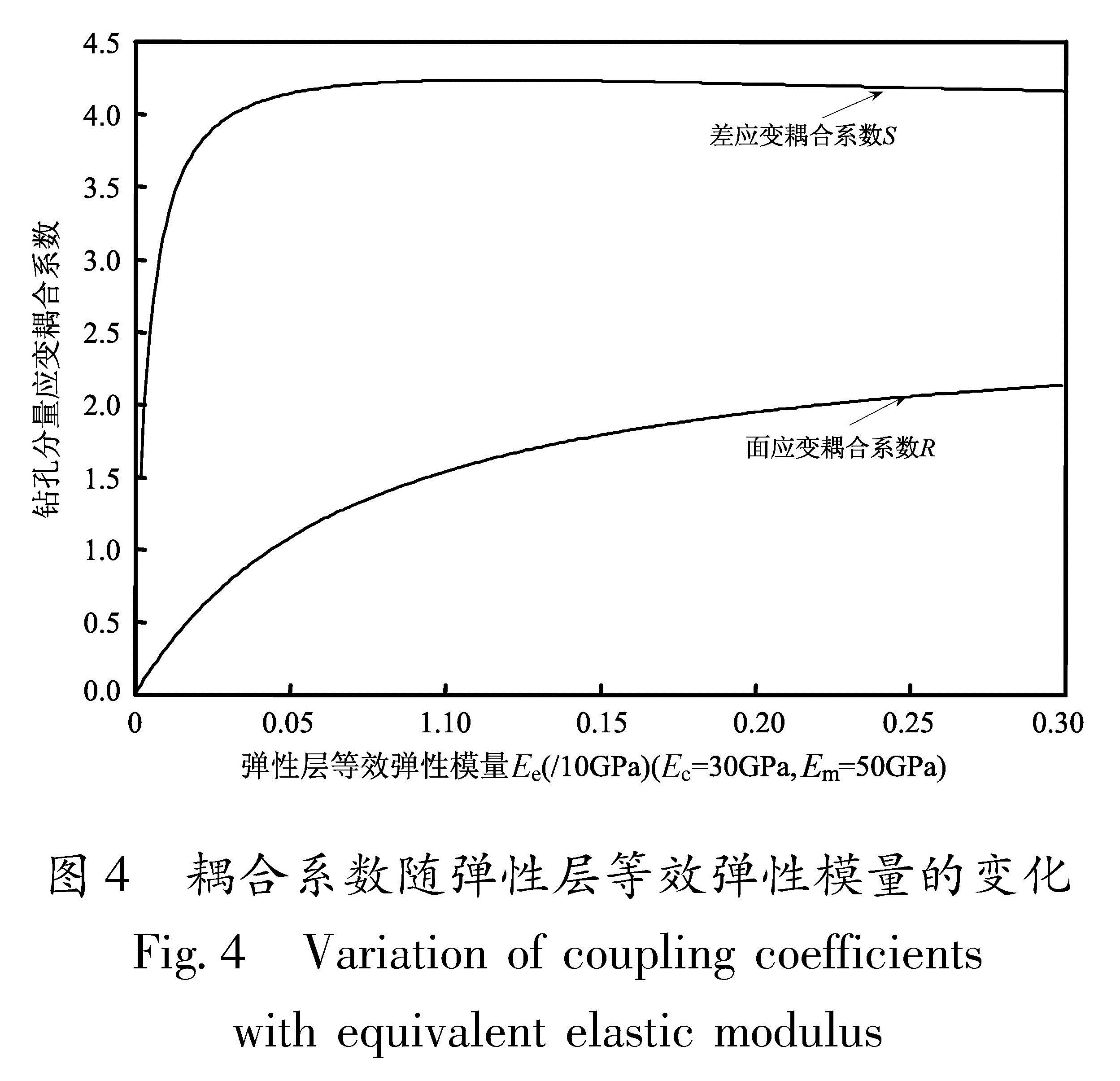
考虑原地应力卸载影响,可以利用4层介质组合模型定量分析钻孔耦合介质中弹性层等效弹性模量Ee对耦合系数R和S的影响。假设水泥弹性模量Ec=300 GPa,地层弹性模量Em=50 GPa,弹性层的泊松比为0.25,在图4中给出了RYR-4钻孔应变的耦合系数R、S随弹性层等效弹性模量变化的关系曲线,从图中可以看出,面应变耦合系数R随Ee增加而上升但上升趋势变缓,差应变耦合系数S随Ee增加先快速上升后出现下降变化。
在应力由地层向测量钢筒传递过程中,由于钻孔的应力集中作用,地层介质和水泥介质对应力的传递起阻隔作用,考虑到原地应力卸载作用,卸载弹性层对差应变耦合系数S起放大作用而对面应变耦合系数R起衰减作用,弹性层等效弹性模量Ee越小影响越显著。3 RYR-4钻孔分量应变的观测结果分析
由于存在日、月引潮力对地表的加卸载作用,在钻孔应变观测中可以记录到清晰的固体潮,虽然真实的潮汐力无法知道,但是理论潮汐力可以精确的计算,在对钻孔应变观测的分析研究中,假设理论潮汐应力等同于真实的潮汐力,通过对观测资料进行潮汐调和分析,可以计算出某一频段潮汐波观测振幅与理论振幅的比值。对于四分量钻孔应变,分别以相互垂直的1#、3#和2#、4#组合的和应变代替观测的面应变,通过面应变固体潮M2波振幅理论值对其进行调和分析,计算的固体潮M2波潮汐因子f即为面应变耦合系数R的观测值。
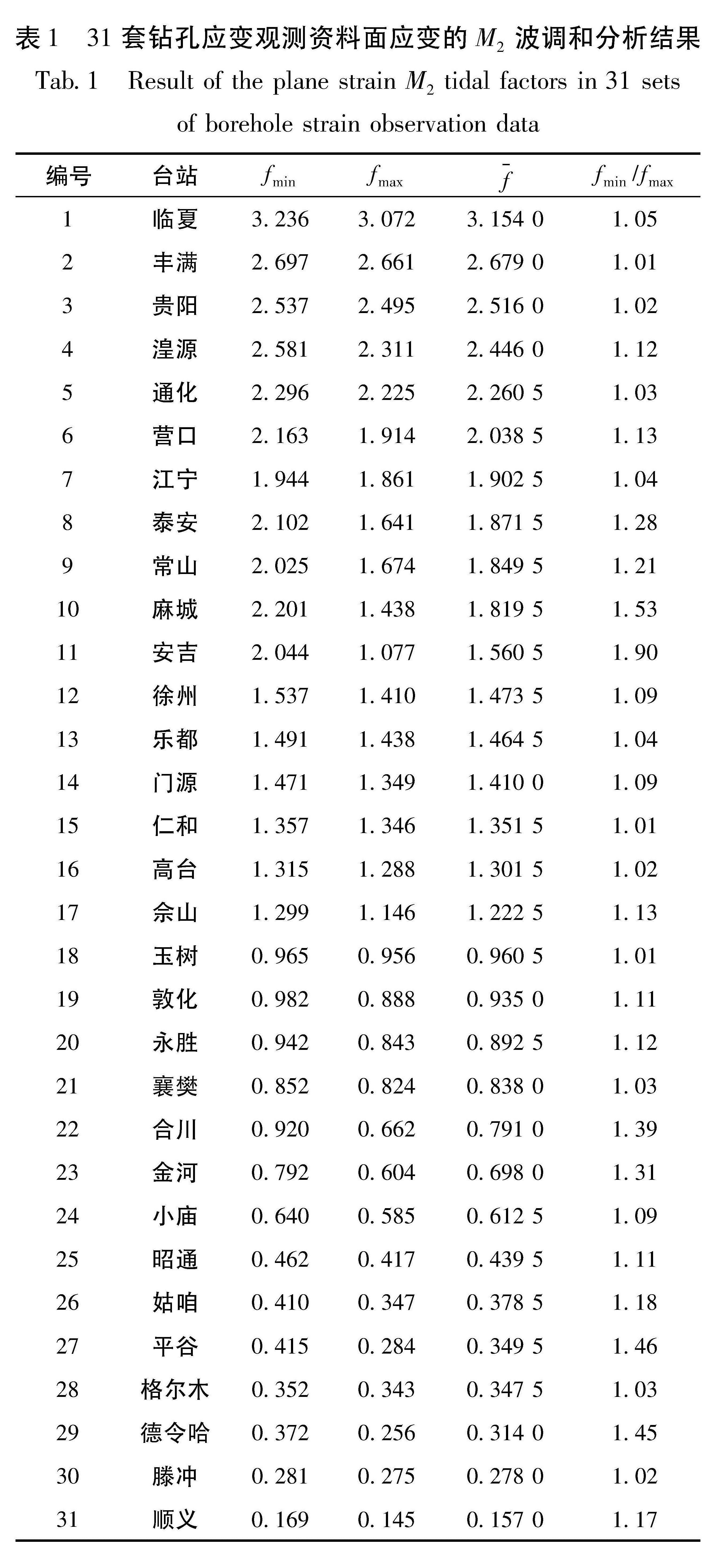
表1给出了31个台站RYR-4钻孔分量应变的M2波面应变潮汐因子,从表中可以看出,同一台站潮汐因子的最大值与最小值也不完全相等,其中安吉台相差接近1倍; 不同台站观测的潮汐因子大小也不一样,最大值是临夏台的3.15,最小值是顺义台的0.16,两者相差约20倍。因为顺义台附近的昌平台体应变记录到清晰的固体潮,很难给出顺义台观测不到潮汐力的合理解释。
通过对观测结果进行对比分析,发现出现潮汐因子高值的台站多位于背景应力场较弱的大陆东部地区,而潮汐因子低值台站多位于背景应力场较高的南北地震带附近。利用4层介质钻孔模型也可以对该现象进行合理解释,原地应力越高,对钻孔卸载影响越显著,潮汐因子观测值也越小。依据式(19),由于耦合介质存在非均匀各向异性,各台站观测的组和面应变由于叠加了差应变,潮汐标定方法计算的两组面应变耦合系数存在一定的偏差,当实际面应变耦合系数相对较小时,若利用面应变潮汐理论值对观测资料进行拟合计算,耦合系数可能会出现负值。表1 31套钻孔应变观测资料面应变的M2波调和分析结果
Tab.1 Result of the plane strain M2 tidal factors in 31 sets of borehole strain observation data4 主要结论
在钻孔应变观测中受到各种环境因素影响,原地构造应力对钻孔开挖的卸载作用,对应力传递起到衰减作用,造成钻孔应变观测值远小于真实值。本文所利用的4层介质钻孔模型对原有的3层介质模型进行改进,依据应力函数法研究了耦合介质弹性性质变化对钻孔耦合系数的影响,通过与观测结果对比分析,主要得出以下结论:
(1)4层介质耦合的钻孔模型较接近真实观测条件,通过分析耦合介质弹性性质变化与钻孔的耦合系数的关系,发现耦合系数的大小主要受耦合介质弹性性质的影响。
(2)受原地应力卸载作用钻孔围岩塑性层的等效弹性模量相对地层弹性模量发生较大变化,该弹性层等效弹性模量的变化对面应变耦合系数影响较大,对差应变耦合系数影响相对较小。
(3)利用4层介质钻孔模型可以对观测结果进行合理解释,钻孔耦合系数的大小和台站背景应力场存在一定联系。
本文在撰写过程中得到苏恺之研究员和池顺良研究员的帮助,在此向他们表示衷心感谢。
- 艾凯,刘元坤,景锋.2003.软弱岩体钻孔变形测试研究[J].岩土力学,24(增刊):242-244.
- 蔡美峰.2011.岩石力学与工程[M].科学出版社,307-326.
- 池顺良,武红岭,骆鸣津.2007.钻孔应变观测中潮汐因子离散性与各向异性原因探讨[J].地球物理学进展,22(6):1746-1753.
- 高龙生.1973.利用钻孔形变测量介质中应力场[J].地球物理学报,16(1):25-42.
- 李玉江,陆远忠,陈连旺,等.2011.钻孔应变观测影响因素的数值模拟分析[J].大地测量与地球动力学,31(1):35-38.
- 骆鸣津,迟顺良,马鸿均.2008.地层绝对应力测量与钻孔应变测量[M].北京:地震出版社,66-79.
- 骆鸣津,顾梦林,李安印,等.1989.用引潮力进行钻孔的应变—应力的原地标定[J].地壳形变与地震,9(4):51-62.
- 潘立宙.1981.与地应力测量有关的几个公式的推导和讨论[A]// 中国地质科学院地质力学研究所,国家地震局地震地质大队.地应力测量原理与应用[C].北京:地质出版社,163-203.
- 秦向辉,谭成轩,孙进忠,等.2012.地应力与岩石弹性模量关系实验研究[J].岩土力学,33(6):1689-1695.
- 邱泽华,石耀霖,欧阳祖熙.2005.四分量钻孔应变观测的实地绝对标定[J].地震,25(3):27-34.
- 徐芝纶.2006.弹性力学(上)[M].北京:高等教育出版社,54-67.
- 余寿文,冯西桥.1997.损伤力学[M].北京:清华大学出版社,78-96.
- 张晶,刘琦.2012.钻孔应变差应变耦合系数反演与有关机理的探讨[J].大地测量与地球动力学,32(2):155-159.
- 张凌空,牛安福.2013.分量式钻孔应变观测耦合系数的计算[J].地球物理学报,56(9):3029-3037.
- Gladwin M.T.,Hart R..1985.Design Parameters for Borehole Strain in Strumentation[J].Pure Appl.Geophys.,123(1):59-80.
- Hart R.H.G.,Gladwin M.T.,Gwyther R.L..1996.Tidal Calibration of Borehole Strain Meters:Removing the Effects of Small-scale Inhomogeneity[J].J.Geophys.Res.,101(Bll):25 553-25 571.
- Hodgkinson K.,Langbein J.,Henderson B.,et al.2013.Tidal Calibration of Plate Boundary Observatory Borehole Strainmeters[J].J.Geophys.Res.,118:447-458,doi:10.1029/2012 JB009651.
- Langbein J..2010.Effect of Error in Theoretical Earth Tide on Calibration of Borehole Strainmeters[J].Geophys.Res.Let.,37(21):L21303,doi:10.1029/2010GL044454.
- Roeloffs E..2010.Tidal Calibration of Plate Boundary Observatory Borehole Strain Meters:Roles of Vertical and Shear Coupling[J].J.Geophys.Res.,115(B06405),doi:10.1029/2009JB006407.