摇摆墙体系为新型可复位抗震结构(吕西林等,2011; 周颖,吕西林,2011),已有工程实例,并有学者进行了摇摆墙体系的抗震性能研究,认为摇摆墙能使原结构各层变形趋于一致,有效控制变形集中(曹海韵等,2011; 曲哲,叶列平,2011; 曲哲等,2011),可发挥结构整体抗震及耗能能力。Patil和Jangid(2005)介绍了多自由度体系的导管架海洋平台采用多种被动控制装置,如粘弹性阻尼器、粘滞阻尼器以及摩擦阻尼器等在遭受波浪荷载作用时的减振效果较好。Ma等(2010)提出了ETMD减振系统,是利用装置内部设备进行控制的,结果表明ETMD减振系统在适当的频比和质量比条件下具有较好的减振效果,但是ETMD系统受频率限制比较大,控制频域宽度很窄。Jin等(2007)研究了利用TLD对导管架海洋平台进行抗震分析,并进行了试验研究和数值分析,结果表明TLD的晃动频率与平台的自然频率比值是控制抗震的关键因素,TLD的水与平台的质量比越大越有利于减震。综上所述,由于平台的结构刚度较大且摩擦阻尼器、粘滞阻尼器、粘弹性阻尼器等为位移型或速度型阻尼器,在导管架海洋平台不易发挥作用,TMD和TLD在海洋平台结构的减震是有条件的。结合摇摆墙结构的优点,本文提出一种新型海洋平台—摇摆墙结构体系(张纪刚等,2012,2013),提出在摇摆墙铰接处设置粘弹性转角阻尼器进行减震控制。

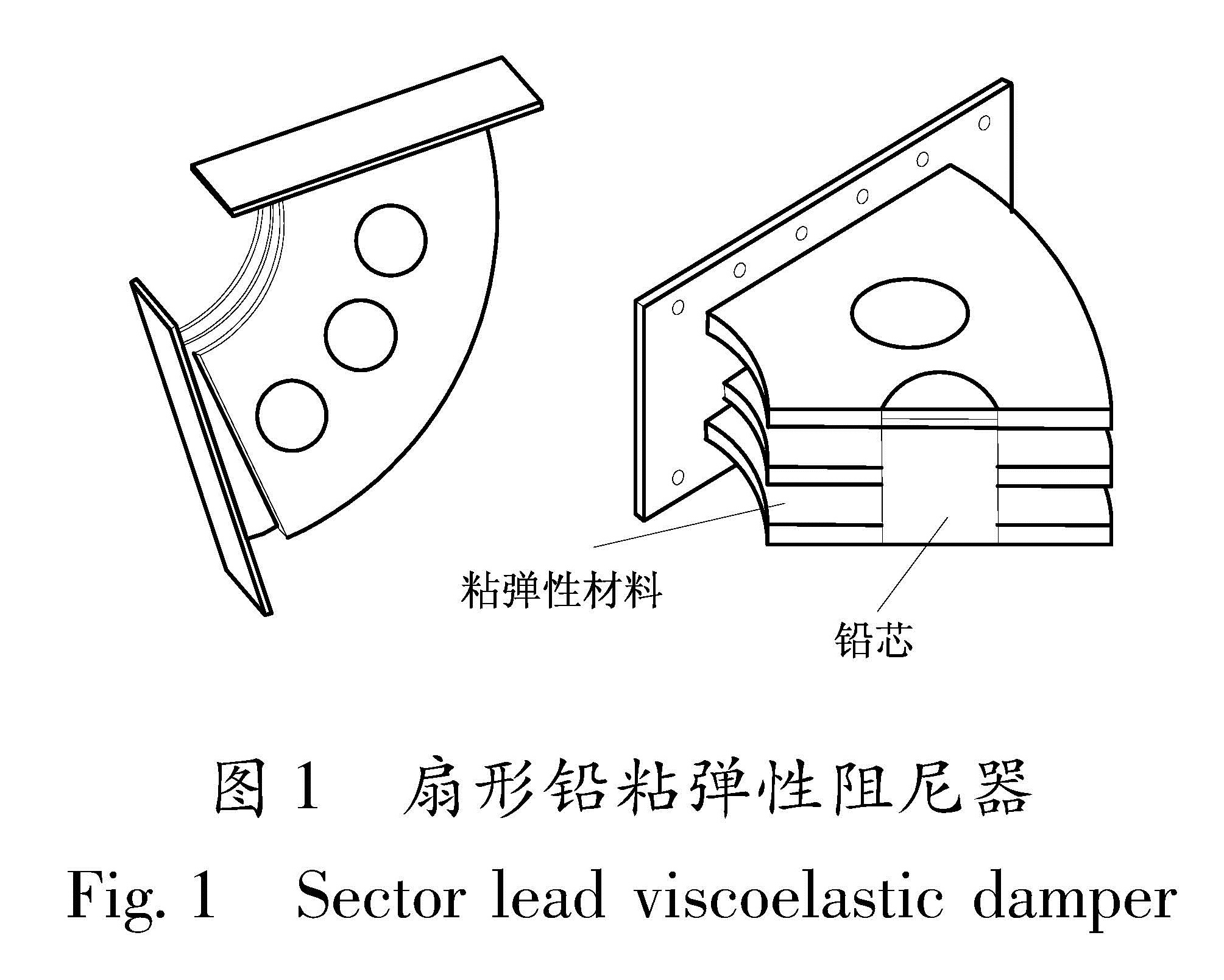
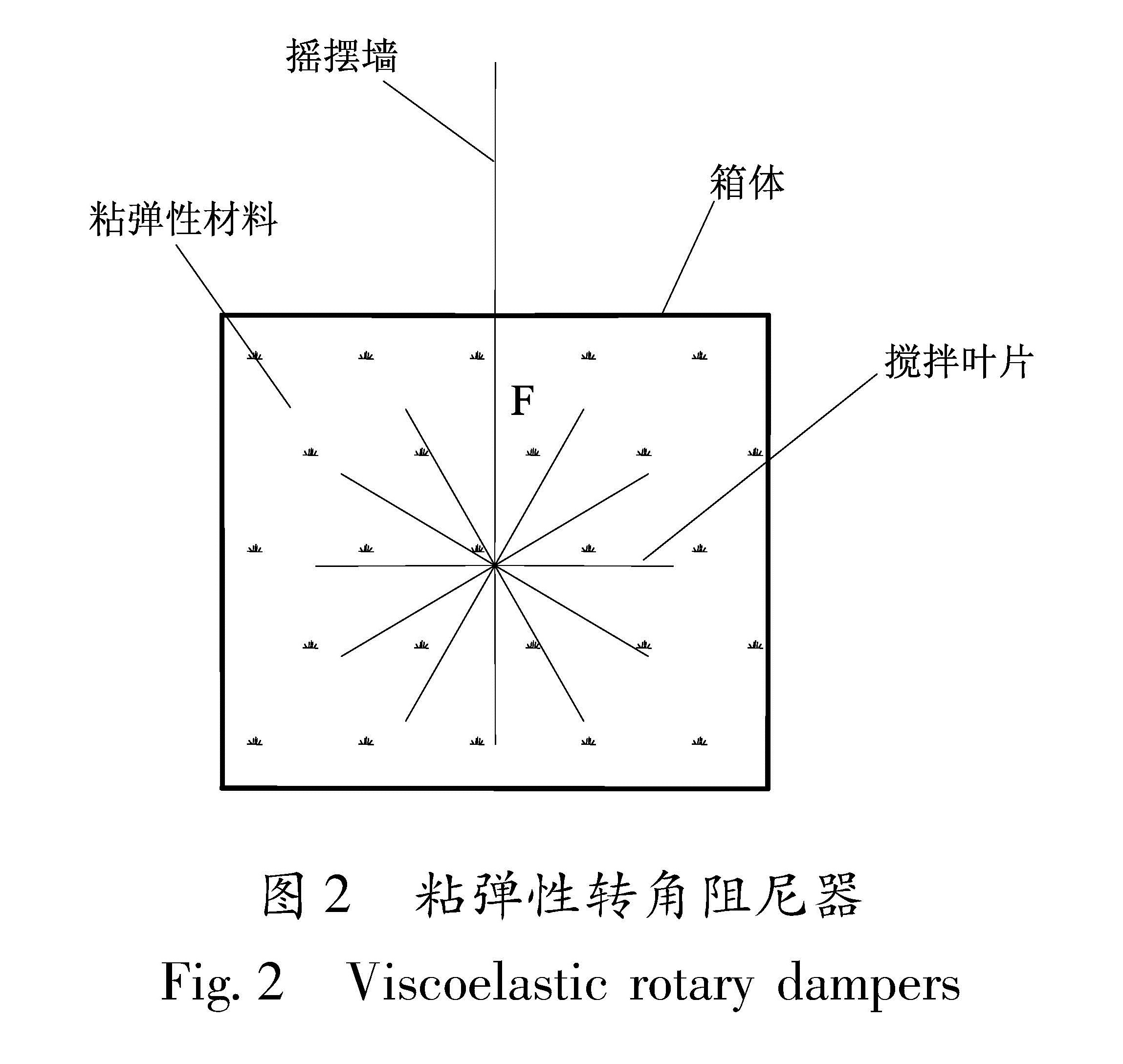
目前大部分阻尼器都是直线拉压型,专用于控制转动自由度的阻尼器还比较少,近年来也有相关学者提出了多种新型转角阻尼器,具有较好的设计方案和动力学性能。徐昕等(2012)提出一种扇形铅粘弹性阻尼器(图1),该阻尼器既有粘弹性材料的速度相关型特点,又有金属阻尼器的大阻尼特性,是一种非常适合本研究的阻尼器。本文另提出一种新型粘弹性转角阻尼器的构造,其构造简图见图2。图2为图4中H点处细部构造,在图4所示铰接点H处布置一个箱体,箱体可根据实际需求延纸面方向延长,内部充满高粘稠度粘弹性材料或者粘滞流体,在摇摆墙根部焊接若干搅拌叶片,叶片可根据阻尼的需求调整个数和大小,当摇摆墙发生转动时,摇摆墙带动叶片,搅动箱体内的高粘稠性阻尼材料,产生巨大的阻尼力,从而耗散振动能量。

阻尼器的布置形式是多变的,由于海洋平台—摇摆墙体系相对位移较小,而摩擦、金属阻尼器等都是位移相关型阻尼器,本文将阻尼器布置于摇摆墙底部的铰接点处,摇摆墙只有转动自由度,且转动位移较小,因此选用速度相关型的粘弹性转角阻尼器进行耗能减震,并利用ANSYS来进行有限元计算。

图1 扇形铅粘弹性阻尼器
Fig.1 Sector lead viscoelastic damper

图2 粘弹性转角阻尼器
Fig.2 Viscoelastic rotary dampers

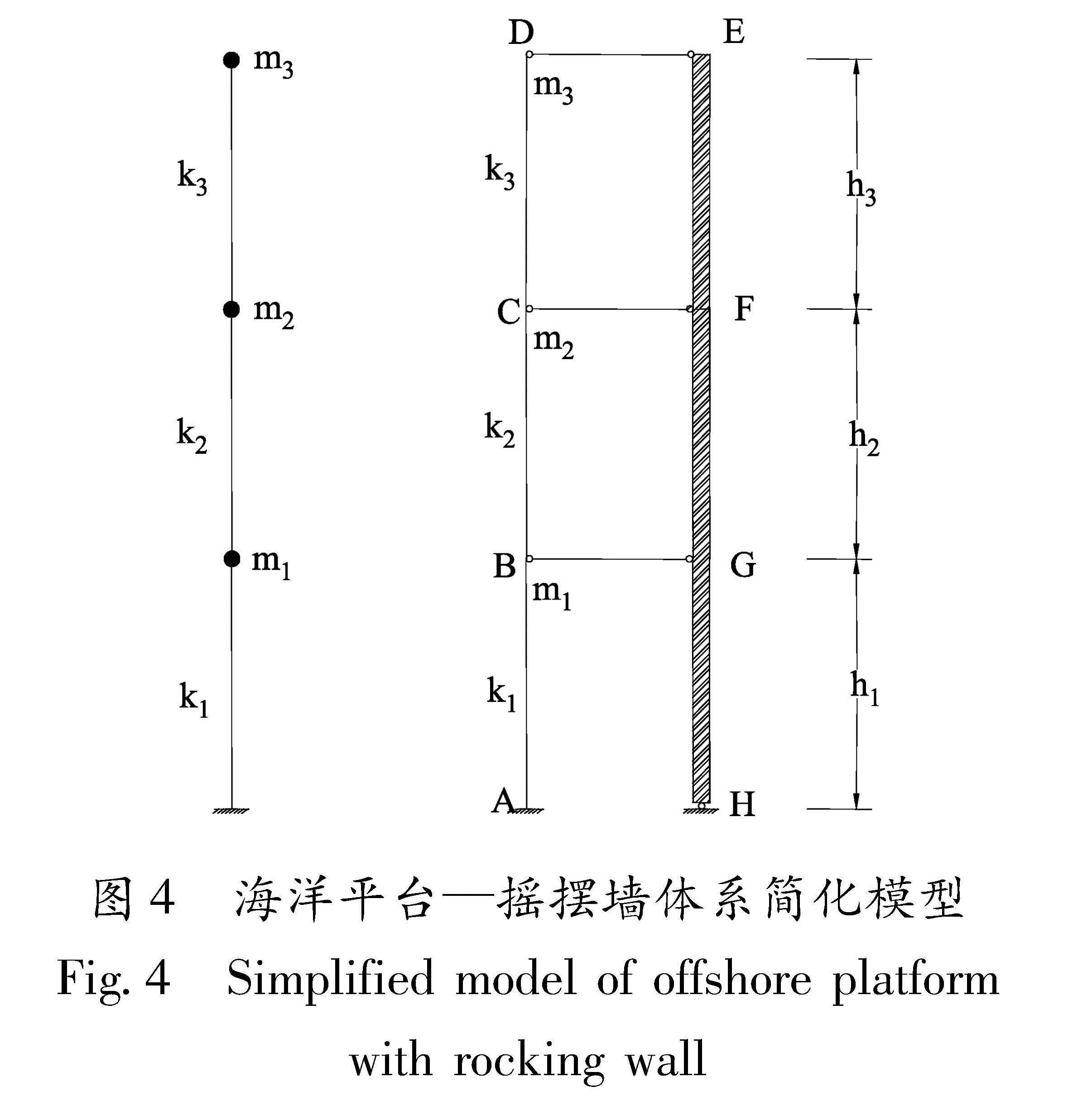
图3为海洋台平—摇摆墙体系原型,经简化选取如图4所示的三层海洋平台摇摆墙体系,其中AD为海洋平台原结构,EH为摇摆墙,BG、CF、DE为链杆,A点固接,B、C、E、F、G、H点均为铰接。AD、EH、BG、CF、DE均选用BEAM23单元,质量m₁、m₂、m₃为MASS21单元。为简化计算,取层高h₁=h₂=h₃=2 m,m₁=m₂=m₃=100 kg,AD弹性模量为E₁=2×10¹¹ N/m²; 为使高阶自振频率稳定,取EH弹性模量为E₂=2×10¹⁸ N/m²,AD、EH的惯性矩均取为I₁=I₂=4.5×10^-8 m⁴。

以图1和图2所示阻尼器为模型基础,与图4所示海洋平台简化模型相结合,根据经典的粘弹性材料的开尔文模型,在H点处粘弹性阻尼器应用COMBIN14单元,设置H点阻尼器的单元属性为垂直于纸面的ROTZ方向单自由度抗扭转模型,在H点阻尼器处提供抵抗变形的扭矩。采用3条经典的地震波——天津波(EW)、El-Centro波和Taft波进行抗震性能验算,不改变3条波的频谱特性,仅将3条波的地面运动最大加速度选为2.2 m·s^-2。

图3 海洋平台—摇摆墙体系
Fig.3 Offshore platform with rocking wall

图4 海洋平台—摇摆墙体系简化模型
Fig.4 Simplified model of offshore platform with rocking wall

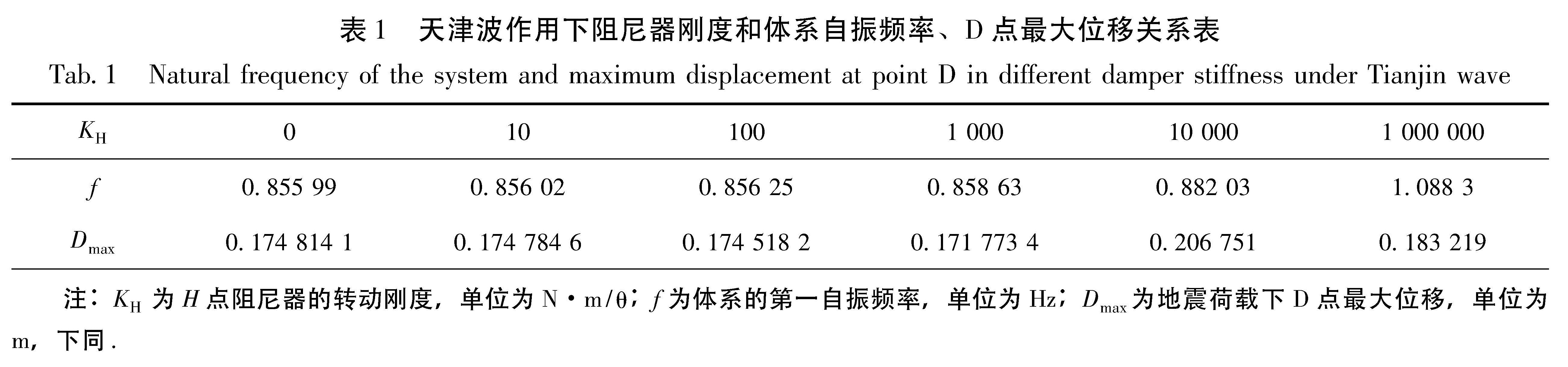
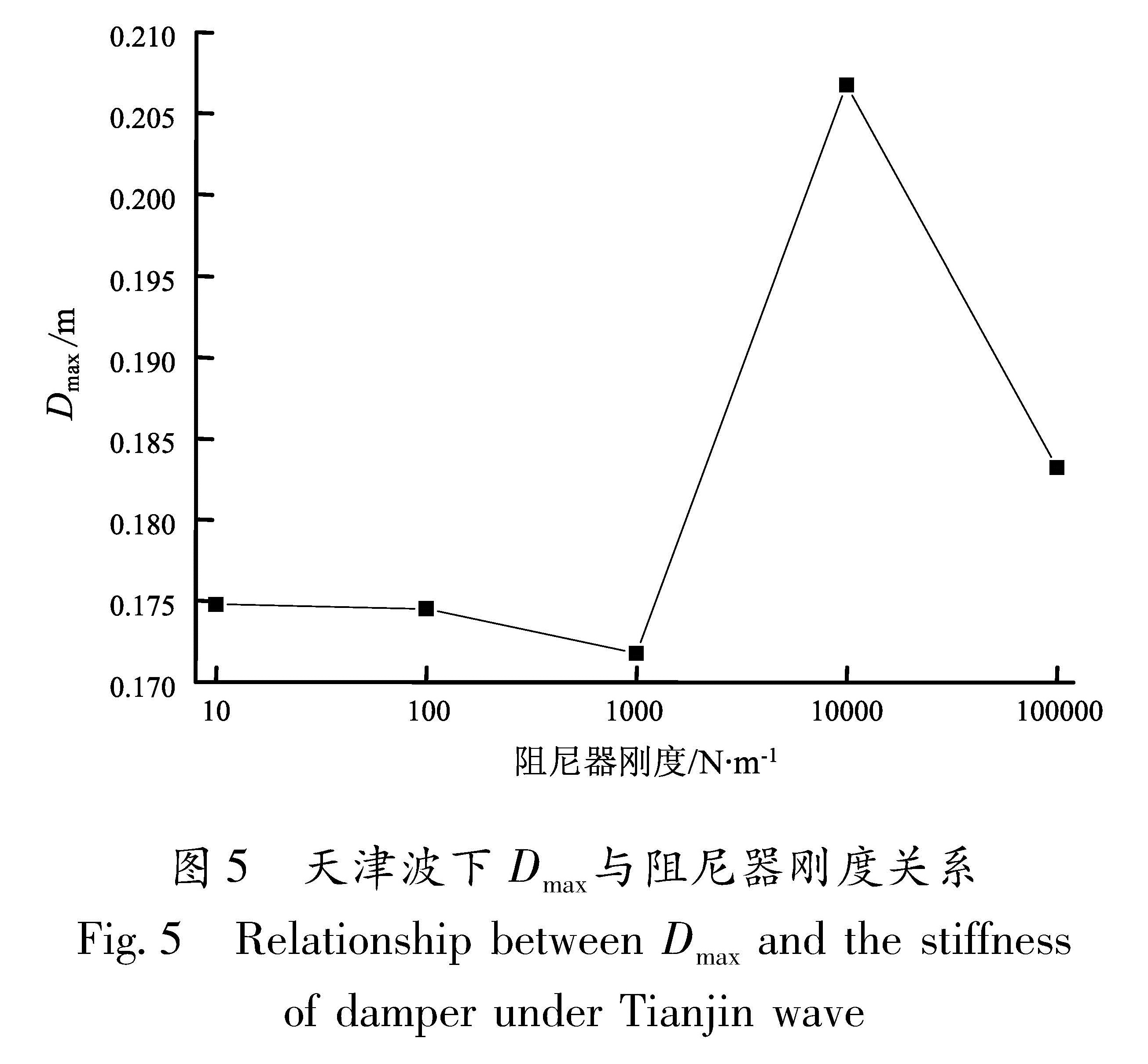
首先计算在H点(粘弹性阻尼器)无阻尼器情况下体系对天津波(EW)的反应,保持H点阻尼为0,依次增大H点刚度,为简便计算,分别计算H点刚度值K_H分别为0、10、10²、10³、10⁴和10⁵ N·m/θ时,体系的地震反应和结构自振频率的变化,结果见表1、图5。

表1 天津波作用下阻尼器刚度和体系自振频率、D点最大位移关系表
Tab.1 Natural frequency of the system and maximum displacement at point D in different damper stiffness under Tianjin wave

图5 天津波下Dmax与阻尼器刚度关系
Fig.5 Relationship between Dmax and the stiffness of damper under Tianjin wave

图6 天津波下Dmax与阻尼器转动阻尼关系
Fig.5 Relationship between Dmax and the rotary damping of damper under Tianjin wave

由频率的计算公式ω_n=((k^*)/(m^*))^1/2可知,体系的自振频率随着阻尼器刚度的增大而增大; 尽管刚度越大,阻尼器的输出力越大,但是增大的阻尼器刚度并没有给体系的地震反应带来实质性的减小,反而当K_H=10⁴时,地震反应增大,根据天津波频谱特性可知,当体系自振频率在0.856～1.089 Hz之间,地震的动力系数处在较高水平当中,体系地震反应不稳定,极易发生共振,因此单纯增加阻尼器刚度是不合理的。

保持H点阻尼器刚度为0,依次增大H点阻尼,为简便计算,分别计算取H点转动阻尼值C分别为0、10、10²、10³、10⁴和10⁵ N·m·s/θ时,体系的地震反应和结构自振频率的变化,结果见表2、图6。

由表2和图6可知,在天津波作用下,D点最大位移随着阻尼器转动阻尼的增大而减小,阻尼的存在有减小结构地震反应的作用,并且随着阻尼比的增大,结构的地震反应有继续减小的趋势,根据结构动力学原理,当阻尼增大到一定程度时,结构将锁闭,不会发生振动。但是,阻尼器的阻尼不会无限制增大,也很难出现使结构完全锁闭的情况,并且在很多情况下,经济性也是很多大阻尼器的限制条件,由图6可知,随着阻尼的增大,D点最大位移的减小量递减,也就是说阻尼越大,单位阻尼对减振控制的贡献越小,经济性越差。

为了更好地说明问题,下面给出如图4所示结构在EL-CENTRO波和TAFT波下的振动情况,见表3～6、图7～10。

表2 天津波作用下阻尼器阻尼、阻尼比、D点最大位移关系表
Tab.2 Damping ration and maximum displacement at point D in different damping of damper under Tianjin wave

注:C_H为H点阻尼器的转动阻尼,单位为N·m·s/θ; ζ为体系的阻尼比,下同.

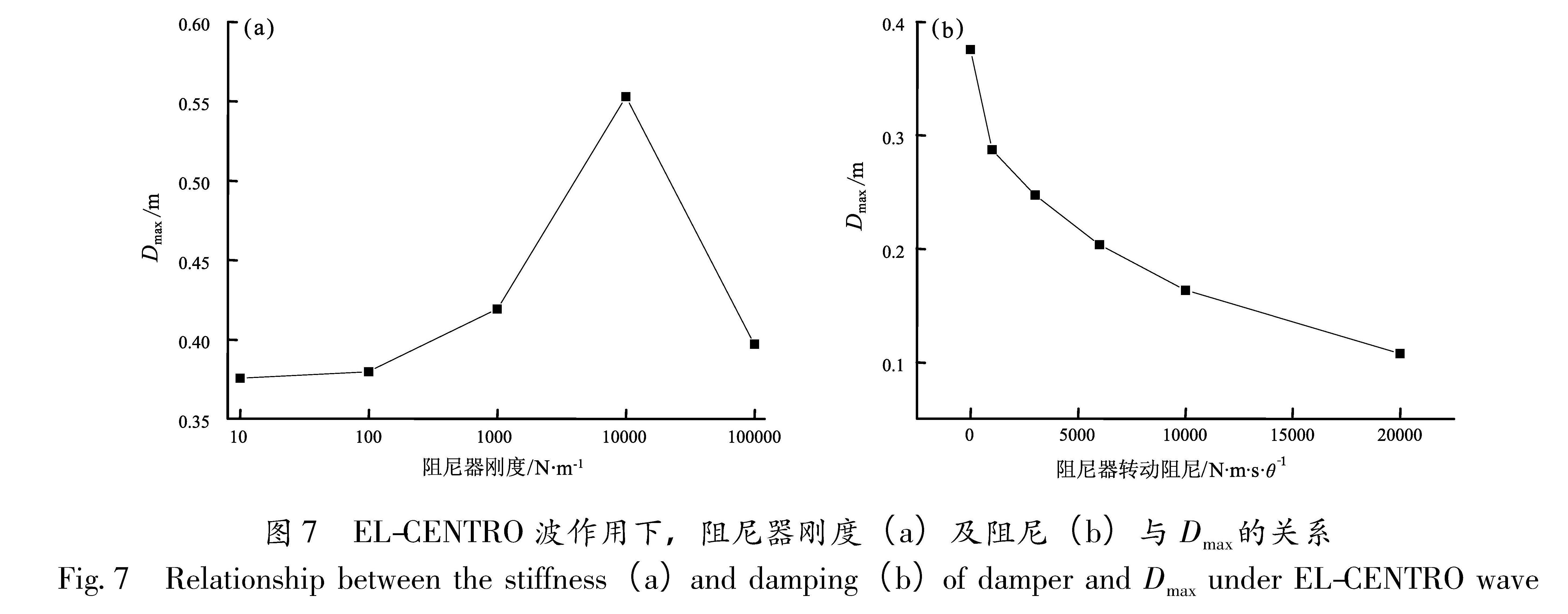
表3 EL-CENTRO波作用下阻尼器刚度和Dmax关系
Tab.3 Relationship between the stiffness of the damper and Dmax under EL-CENTRO wave

表4 EL-CENTRO波作用下阻尼器阻尼和Dmax关系
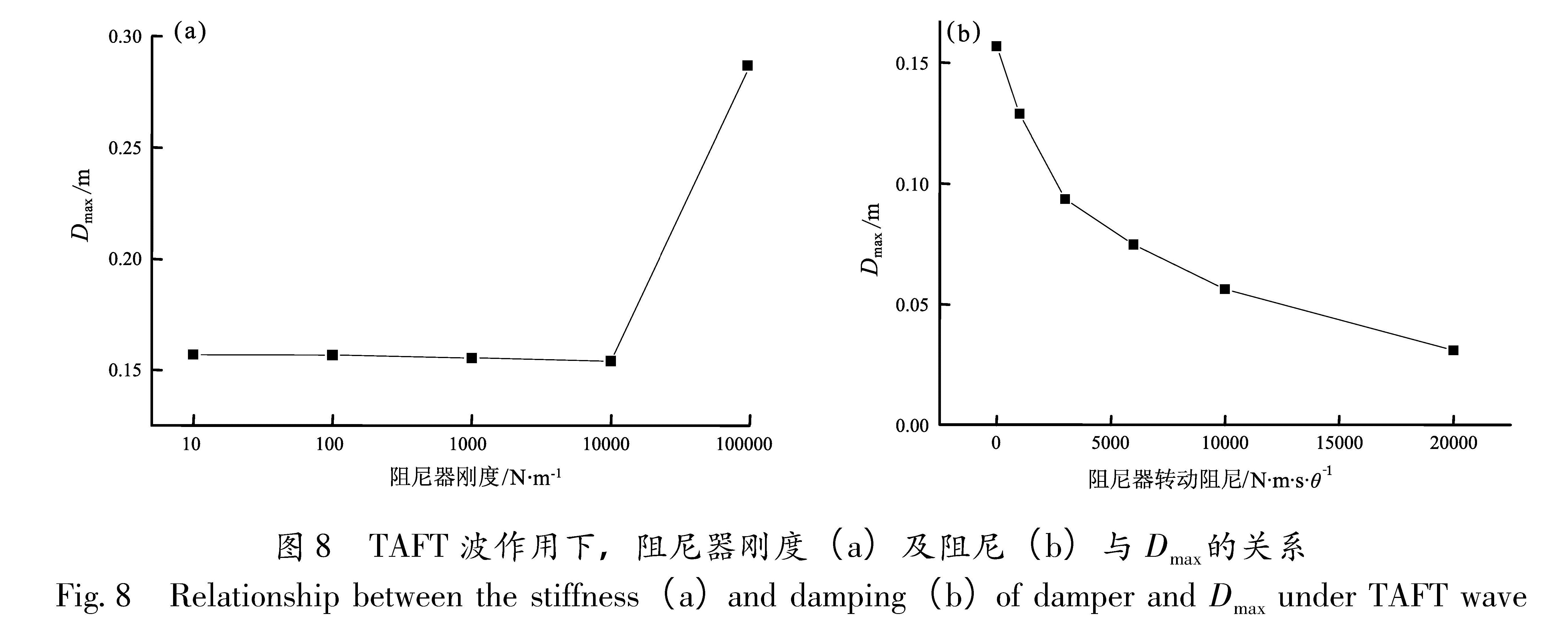
Tab.4 Relationship between the damping of the damper and Dmax under EL-CENTRO wave

表5 TAFT作用下阻尼器刚度和Dmax关系
Tab.5 Relationship between the stiffness of the damper and Dmax under TAFT wave

表6 TAFT作用下阻尼器阻尼和Dmax关系
Tab.6 Relationship between the damping of the damper and Dmax under TAFT wave

由表3、图7a和表5、图8a可知,在不同的地震波激励下,尽管结构自振频率的规律保持不变,阻尼器刚度对体系的抗震性能的影响依然是没有规律的,因此在实际工程中,应当首先测量平台所在位置的海底场地的卓越周期,综合考虑平台自身的刚度、粘弹性转角阻尼器的刚度和平台的质量等参数,使自振周期避开场地的卓越周期,以降低发生共振的概率。由表4、图7b

和表6、图8b可知,即便是在动力系数比较大的EL-CENTRO波作用下,转角阻尼的存在也会给体系的抗震性能带来本质上的提升,但过大和过小的阻尼都会产生不利效果,所以实际中还需根据结构的抗震需求合理设计阻尼。下面选择天津波和TAFT波,取K_H=10³ N·m/θ、C_H=10⁵ N·m·s/θ进行抗震验算,对有无阻尼器的情况进行对比,结果见图9。

图7 EL-CENTRO波作用下,阻尼器刚度(a)及阻尼(b)与Dmax的关系
Fig.7 Relationship between the stiffness(a)and damping(b)of damper and Dmax under EL-CENTRO wave

图8 TAFT波作用下,阻尼器刚度(a)及阻尼(b)与Dmax的关系
Fig.8 Relationship between the stiffness(a)and damping(b)of damper and Dmax under TAFT wave

图9 Taft波(a)和天津波(b)作用下,有无阻尼器D点位移对比
Fig.9 Contrast of displacement of point D with and without damper under Taft(a)and Tianjin(b)wave

本文通过对海洋平台—摇摆墙体系中摇摆墙铰接点处安装粘弹性转角阻尼器进行了有限元分析,并对阻尼器参数进行了简单优化,可得出如下结论:

(1)在摇摆墙底部铰接点处安装转角阻尼器对海洋平台摇摆墙体系的抗震性能具有显著效果。

(2)可以通过调节阻尼器的刚度来调整结构的自振频率,以降低结构与地震发生共振的概率; 可以根据经济等情况综合考虑调节阻尼器阻尼以达到最好的消能减震效果。

(3)阻尼器的构造和性能还需进一步优化。