基金项目:“十二五”国家科技支撑计划项目(专题七2012BAK19B01-07)和地震科技星火计划项目(XH14051YSX,XH13024Y)联合资助.
(1.中国地震局兰州地震研究所,甘肃 兰州 73000; 2.宁夏回族自治区地震局,宁夏 银川 750001; 3.福建省地震局,福建 福州 350001)
(1. Lanzhou Institute of Seismology,CEA,Lanzhou 730000,Gansu,China)(2. Earthquake Administration of Ningxia Hui Autonomous Region,Yinchuan 750001,Ningxia,China)(3. Earthquake Administration of Fujian Province,Fuzhou 350002,Fujian,China)
northeastern margin of the Tibetan Plateau; noise source; empirical Green's function; signal-to-noise ratios; normalized average energy flux
备注
基金项目:“十二五”国家科技支撑计划项目(专题七2012BAK19B01-07)和地震科技星火计划项目(XH14051YSX,XH13024Y)联合资助.
采用2009年青藏高原东北缘55个数字化宽频带地震台站的垂直分量波形数据,计算了台站间噪声互相关函数,得到了Rayleigh经验格林函数。利用信噪比和归一化平均能量流的方法分析了青藏高原东北缘背景噪声源的方位分布和季节性变化特征。结果 表明,5~10 s周期噪声源方位分布上较为稳定,不随季节变化,噪声源能量集中在105°~165°方向上,噪声源主要来自于太平洋。10~20 s周期噪声源季节性变化特征明显,夏季的噪声能量主要集中在165°~210°方向上,噪声源来自于印度洋海洋活动; 冬季主要集中在300°~350°和165°~210°方向上,噪声能量主要来源于太平洋和北大西洋。
Basing on the vertical component waveforms recorded by 55 digital broadband seisimic stations located at the northeastern margin of the Tibetan Plateau,we calculate the cross-correlation Green functions of ambient seismic noise between two stations,and obtain the Rayleigh wave empirical Green's function. The techniques of signal-to-noise ratios(SNR)and normalized average energy flux of Rayleigh wave are applied to analyze the azimuthal distribution and seasonal variability of ambient noise sources in the northeastern margin of the Tibetan Plateau. In the period of 5~10 s,the azimuthal distribution of noise source is stable,and don't change with the season. The energy of noise source focuses on the azimuth of 105°~165°,which is mainly affected by Pacific Ocean. In the period of 10~20 s,the azimuthal of noise source varies seasonally,and the energy of noise source focuses on the azimuth of 165°~210° in summer and moves to the azimuth of 300°~350° and 165°~210° in winter,which suggests that the noise source may be affected by the Indian Ocean in summer,the Pacific and North Pacific Oceans in winter.
引言
已有研究结果表明,利用两个台站记录到的背景噪声进行互相关计算能够得到台站间的经验格林函数(Weaver,Lobkis,2001; Derode et al.,2003; Snieder,2004; Wapenaar et al.,2004; Roux et al.,2005)。Friedrich 等(1998)研究表明背景噪声主要由面波组成,背景噪声互相关提取的主要是面波信号。因此利用背景噪声互相关方法提取到的面波格林函数可以开展地壳和上地幔的速度结构研究(Shapiro et al.,2005; Yang et al.,2007; Zheng et al.,2008; 房立华等,2009)和监测地下介质波速的变化(Brenguier et al.,2008; Minato et al.,2012)。与天然地震方法相比,背景噪声互相关方法不依赖于时间、地点和地震的分布。
背景噪声提取格林函数的原理要求噪声源随机均匀分布,但是实际上不同周期的噪声源空间方位上各向异性明显(Pedersen,Krüger,2007),且在分布时间上表现为一定的季节性变化特征,因此噪声源呈现非均匀分布(Stehly et al.,2006)。噪声源的这种非均匀分布会影响格林函数和频散曲线提取的可靠性与稳定性(Derode et al.,2003)。因此,有必要研究噪声源的性质和时空分布特征,以减少由于噪声源的不均匀分布和季节性变化对研究地下速度结构和波速变化时所带来的误差(Lin et al.,2008)。地震背景噪声在10~20 s和5~10 s存在两个明显的峰值,这两个短周期带的地震噪声产生机制可能与海浪和海岸的相互作用有关。第一微震带(10~20 s)为海洋沿岸地区的浅部海水受垂直向压力驱动产生,也可能是碎浪击打海岸产生的; 第二微震带(5~10 s)被认为是相同周期、传播方向相反的两列波相互经过非线性叠加产生的(Longuet-Higgins,1950)。Stehly等(2006)选取了北美、西欧和坦桑尼亚台网1年的地震背景噪声连续记录数据,基于背景噪声互相关函数波形的非对称性特征,发现第一微震带(10~20 s)表现出明显的季节性变化特征,噪声能量与海洋深部海水活动有关; 第二微震带(5~10 s)不随时间演化,能量流的空间分布表现明显的方向性,分析认为噪声信号能量主要来源于海岸线附近,并且证实地震噪声是由海浪和海岸的非线性相互作用产生。Yang和Ritzwoller(2008)用信噪比的方法分析认为欧洲、南非、北美和亚洲地区的两个微震带的噪声源能量方向都来自于近海,只是由于不同周期噪声在介质中传播和衰减的快慢不同,导致噪声源能量方向的异同,同时还指出通过1年以上的背景噪声互相关函数的叠加能够提高经验格林函数和背景噪声成像的准确性。Brooks等(2009)利用新西兰2002年冬季背景噪声数据,采用聚束分析方法分析了该地区第二微震带噪声的基阶和高阶Rayleigh面波特征,一般来说在大多数地区第二微震带Rayleigh噪声波场主要由基阶面波组成,认为能够在该地区提取到高阶Rayleigh波是与沿海大陆狭窄边缘深部海水和长周期海浪的作用有关。Pedersen和Krüger(2007)、鲁来玉等(2009)也分别用F-K方法、聚束分析方法分析了芬兰和中国华北地区的背景噪声源的分布特征。
青藏高原东北缘位于青藏地块、鄂尔多斯地块、阿拉善地块和塔里木地块的交界区域,块体之间剧烈的相互作用使该区域构造活动强烈,该区域一直以来都是地球物理学研究的热点区域。自从“十五”期间地震台网的数字化改造后,在青藏高原东北缘布设了大量宽频带数字化地震台站,有学者利用背景噪声对青藏高原东北缘地区进行了速度结构研究(Li et al.,2009; Zheng et al.,2010)。本文通过收集2009年1~12月甘肃、青海和宁夏数字地震台网的55个宽频带台站的垂直向波形数据,计算了台站对之间的经验格林函数,基于背景噪声经验格林函数的非对称性,分析了青藏高原东北缘地区地震背景噪声源能量的空间分布和季节性变化特征。
1 经验格林函数的提取
假设噪声源分布均匀,两个地震台站i和j之间的波形记录的互相关函数和格林函数的关系如下(Sabra et al.,2005; Sabra,2005; Lin et al.,2008):
(dCij(t))/(dt)≈-Gij(t)+Gji(-t)
=-G⌒ij(t)+G⌒ji(-t).(1)
上式等价于
G⌒ij(t)=-(dCij(t))/(dt)0≤t<∞,
G⌒ji(t)=-(dCji(-t))/(dt)0≤t<∞. (2)
其中,C(t)为i、j两个台站波形记录的互相关函数,G(t)为真实格林函数,G⌒(t)为格林函数的估计值,即经验格林函数。G(t)为正向格林函数,G(-t)为逆向格林函数,Gij(t)表示以台站i为假想的震源,t时刻在台站j接收到的格林函数,Gji(t)表示以台站j为假想震源,t时刻在台站i接收到的格林函数。由于噪声源时空分布的影响和介质的滞弹性影响,经验格林函数和真实格林函数是有区别的,所以互相关函数的导数等于经验格林函数(Yao et al.,2006)。由于互相关函数和经验格林函数仅有相位上的差别,为了计算方便,本文以互相关函数作为经验格林函数来分析。
2 数据及方法
本文选取2009年1~12月甘肃、宁夏和青海台网55个宽频带台站垂直分量波形数据(图1)。首先对单台数据进行预处理,依据Bensen等(2007)的数据处理方法,对原始数据去均值、去趋势和去除仪器响应后,对数据进行1 Hz的重采样,然后将数据截取为每天1个文件,进行5~40 s带通滤波,最后对每天的数据进行时域和频域归一化处理,目的是为了去除天然地震、矿震、仪器畸变信号和台站附近场地效应的干扰,
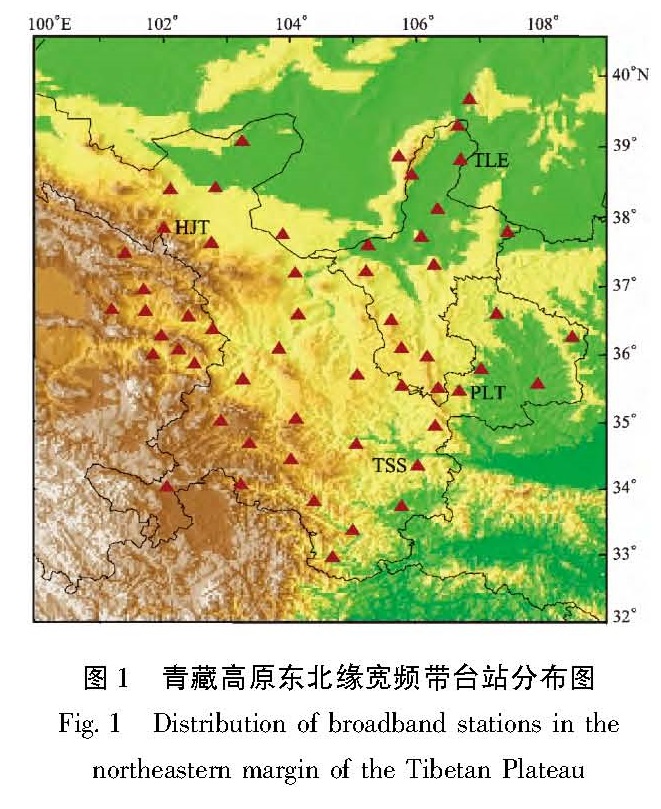
得到更高信噪比的格林函数。时域归一化主要采用滑动绝对平均归一化方法(Running-absolute-mean normalization),频域归一化方法就是首先通过快速傅里叶变换得到振幅谱,然后对振幅谱进行归一化处理,最后傅里叶反变换到时域。频域归一化不仅拓宽了背景噪声的频谱,而且消除了单频信号的干扰。然后计算所有台站对每天的互相关函数,最后完成每个月互相关函数的叠加计算。图1 青藏高原东北缘宽频带台站分布图
Fig.1 Distribution of broadband stations in the northeastern margin of the Tibetan Plateau两个台站垂直分量计算的经验格林函数主要是基阶Rayleigh面波信号,并且有正负两个分支,正分支为因果信号,负分支为非因果信号,两个分支表示波传播的方向是相反的,由于噪声源能量流分布的不均匀性,两个分支的格林函数尽管相位对称,但是振幅不对称,即两个传播方向上的噪声能量强度是不同的,振幅较大的方向噪声能量也比较强。因此可以利用互相关函数正负分支振幅的不对称性来分析噪声源能量的主要来源方向和季节变化特征。
本文主要采用两种方法统计分析噪声能量的空间分布和季节变化特征,这里主要分析青藏高原东北缘地区第一微震带(10~20 s)和第二微震带(5~10 s)的噪声能量特征。第一种方法是以经验格林函数的信噪比来表征噪声能量流的强度,信噪比越大,表示噪声能量强度相对越大。通过计算不同周期和季节经验格林函数的信噪比来估计噪声源能量的强度和方位分布。信噪比定义为信号窗口振幅绝对值的最大值和噪声窗口振幅均方根的比值。信号窗口取Rayleigh面波群速度为2.2 km/s和4.2 km/s之间的经验格林函数的到时窗,噪声窗取信号窗之后的500 s的数据。另外一种方法采用的是Stehly等(2006)提出的使用背景噪声归一化平均能量流的方法来估计噪声能量的相对强度和优势方向。其基本原理是:首先计算经验格林函数信号窗口的最大振幅,这里的信号窗口的选择与前面计算信噪比的方法一致,并且为了补偿Rayleigh面波几何衰减效应,需要乘以台站间距的平方根。然后对加了补偿效应的振幅最大值进行归一化处理,以此作为背景噪声归一化能量流函数。通过计算研究区域所有台站对不同时间段的因果信号和非因果信号的背景噪声归一化能量流,就能够得到整个区域背景噪声能量方向和时间演化特征。
3 青藏高原东北缘背景噪声特征分析
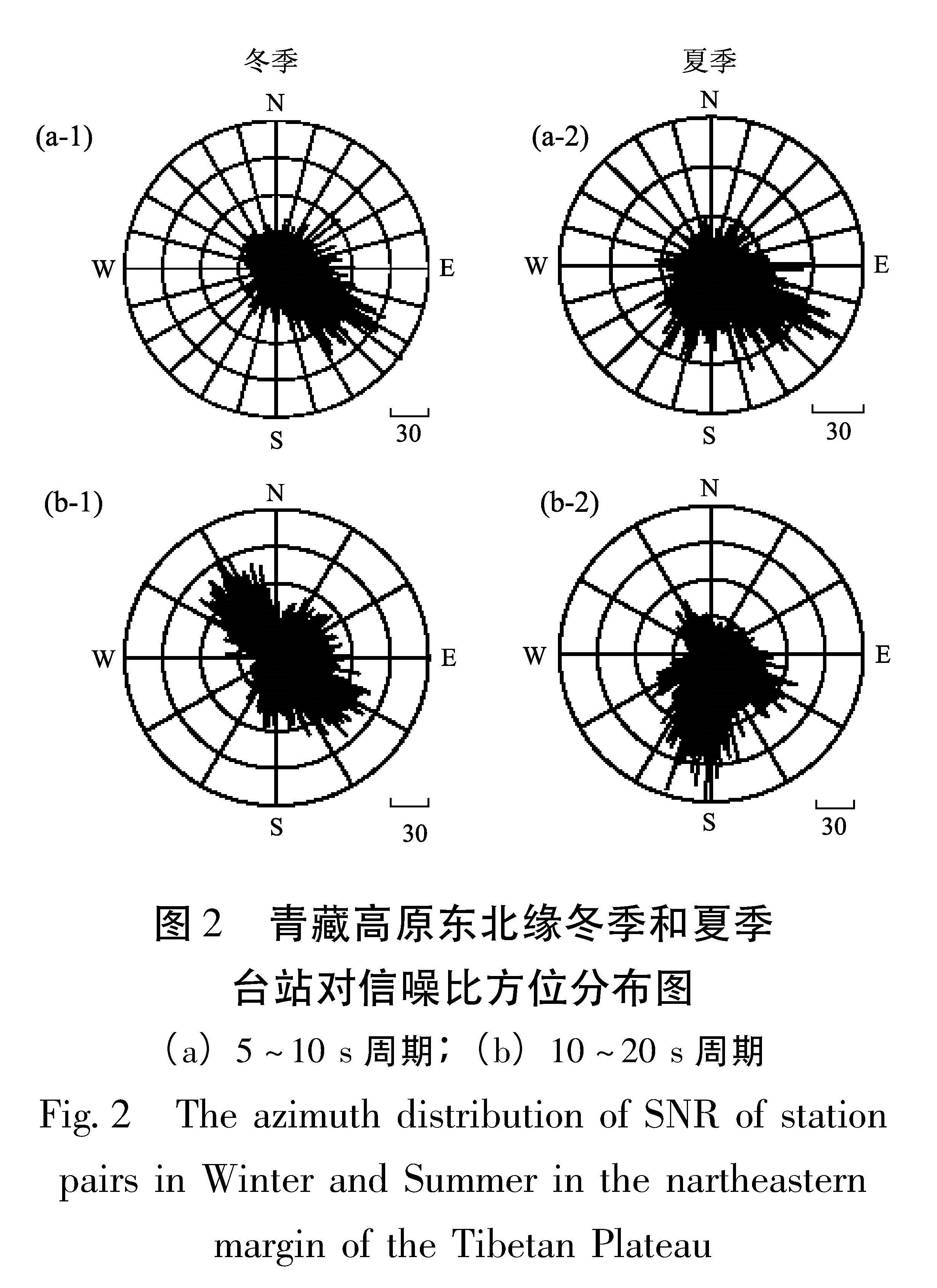
3.1 信噪比方法分析噪声分布特征本文分别利用青藏高原东北缘冬季(2009年1~3月和10~12月)和夏季(2009年4~9月)噪声互相关函数进行叠加计算得到经验格林函数,分析计算了每个台站对5~10 s和10~20 s不同季节的信噪比方位分布,为了避免近场效应,剔除了台站间距小于120 km的台站对。图2给出了所有台站对两个微震带经验格林函数冬季和夏季信噪比的方位分布,极径大小表示信噪比,不同周期的噪声分布表现出不同的季节性特征,第二微震带(5~10 s)背景噪声的优势能量来源全年都集中于105°~165°方位附近,总体来看可能来源于太平洋的海洋活动。第一微震带(10~20 s)背景噪声能量来源表现为明显的季节特征,冬季能量主要来源于300°~350°和105°~165°方向,噪声能量主要来源于北大西洋和太平洋,相对太平洋方向能量较弱; 夏季噪声能量优势方位为165°~210°方向,噪声能量可能来源于印度洋的海洋活动,在105°~165°方向也存在不太明显的能量分布区。
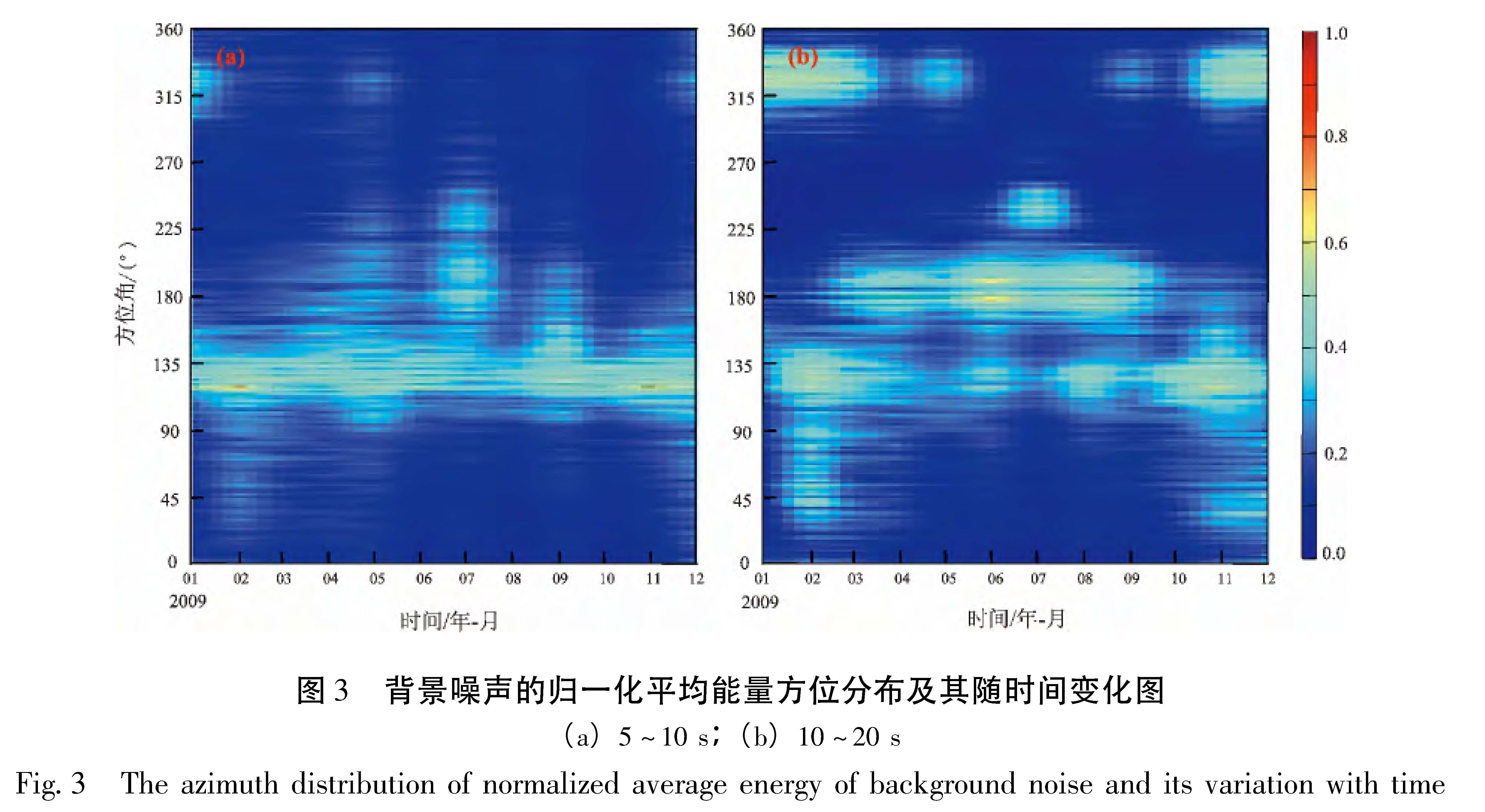
3.2 归一化能量流方法分析噪声分布特征除了用计算信噪比的方法分析噪声的季节性特征,本文还通过计算归一化平均噪声能量流函数分析了噪声能量方位分布和随时间的演化特征。图3为利用2009年1~12月每月的不同方位角的
归一化噪声能量流函数,以每月所有方位角上的经验格林函数最大振幅值进行归一化,归一化后的能量流函数值在0~1之间,这里的噪声能量流函数仅表示平均的噪声能量强度,并不是噪声能量的绝对值。由图4可以看出5~10 s周期的平均
图3 背景噪声的归一化平均能量方位分布及其随时间变化图(a)5~10 s;(b)10~20 s
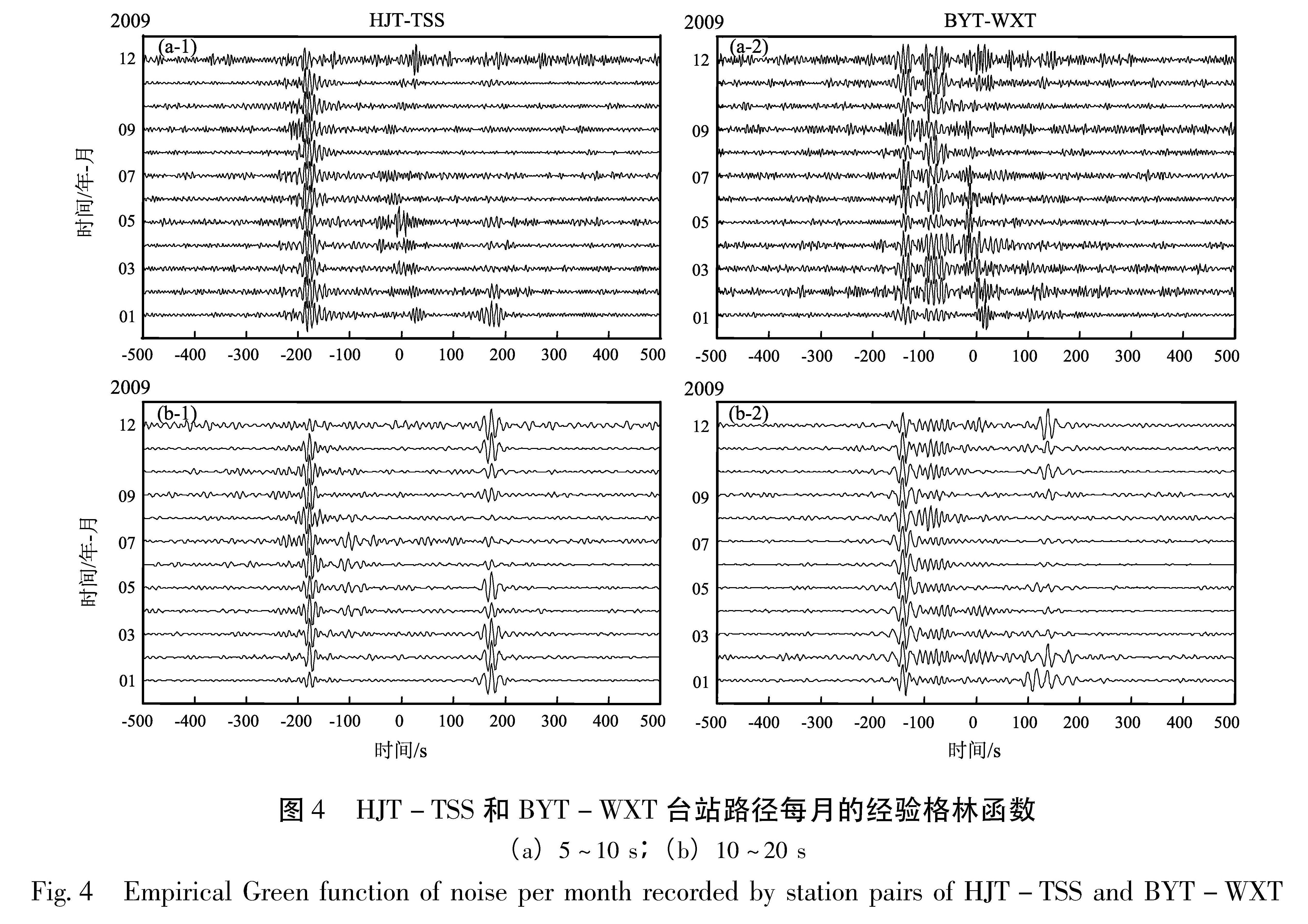
Fig.3 The azimuth distribution of normalized average energy of background noise and its variation with time图4 HJT-TSS和BYT-WXT台站路径每月的经验格林函数(a)5~10 s;(b)10~20 s
Fig.4 Empirical Green function of noise per month recorded by station pairs of HJT-TSS and BYT-WXT噪声能量在冬季和夏季都主要来源于105°~165°方向上的太平洋,这与前面用信噪比方法得出的结论基本一致。而10~20 s周期噪声源的优势能量方向则表现为强烈的季节变化特征。冬季噪声能量分布主要集中在300°~350°和105°~165°方向上,但在105°~165°方向上的能量微弱于300°~350°方向; 夏季主要集中在165°~210°方向,而在105°~165°也存在相对很弱的能量分布,说明噪声能量可能来源于印度洋的海洋活动。
本文还选用了两个特定方向上的台站路径HJT-TSS和BYT-WXT分析了噪声经验格林函数强度变化(图4)。HJT-TSS方向5~10 s周期全年负分支面波信号振幅较大,而正分支几乎没有面波信号,反映出这个方向上的噪声能量主要来源于东南方向的太平洋。而10~20 s周期冬季正负分支面波信号明显,但是夏季只有负分支有高信噪比的信号。BYT-WXT方向为南北向路径5~10 s周期信噪比很差,特别是正分支几乎没有面波信号,而10~20 s周期全年负分支都有清晰的面波信号,而正向面波信号微弱,甚至夏季几乎没有面波信号,这反映了其能量来源受控于印度洋。
从上面的分析还可以看出,第二微震带(5~10 s)噪声源的能量分布比较稳定,方位分布单一。第一微震带(10~20 s)噪声源能量分布随季节性变化明显,表现为方位的多样分布,而且平均能量强度相对高于第二微震带。
4 结论和讨论
(1)青藏高原东北缘地区第二微震带噪声源的位置主要指向太平洋,而第一微震带噪声源位置指向不但包括太平洋,还包括印度洋和北大西洋,说明噪声源主要与海洋活动有关,至于是与近海海水活动还是与远海深部海水活动有关(Kedar et al.,2008),需要进一步的研究。第二微震带的能量来源方位分布较为稳定,不随季节变化,而第一微震带表现了明显的季节性变化,这个特征与Stelhy等(2006)对北美以及Yang和Ritzwoller(2008)对欧洲大陆的研究相吻合,并且在夏季能量来源主要与印度洋的海洋活动有关,冬季噪声能量主要受太平洋和北大西洋的影响,说明印度洋的海洋活动在北半球夏季强于冬季(王伟涛等,2011),而太平洋和大西洋的海洋活动正好相反,这反映了南北半球大洋运动的不同特点。研究还发现10~20 s周期的噪声平均能量强度高于5~10 s的,这可能是由于长周期噪声在传播路径上吸收衰减低于短周期噪声(Yang,Ritzwoller,2008),Yang和Ritzwoller(2008)认为两个微震带噪声源的来源位置可能是一致的,只是长短周期噪声在传播路径上的衰减快慢不同,从而导致了噪声源能量在不同方位上的差异。本文的研究方法仅仅噪声源能量来源的大致方位,精确地定位需要使用F-K和聚束分析方法进行分析。
(2)高分辨率背景噪声层析成像要求射线覆盖均匀,而噪声源分布的方位各向异性,使某些方向噪声互相关函数的信噪比很低,在做成像时可能要舍去这些方向的射线,对成像的分辨率产生影响,进而影响成像结果的可靠性。因此需要长时间互相关函数的叠加以提高经验互相关函数的信噪比,特别是那些噪声源能量分布较弱的方位上的互相关函数,并且使格林函数正负分支更为对称。因此在用背景噪声方法研究青藏高原东北缘地区的地下速度结构时需要考虑噪声源时空分布的复杂性。
(3)青藏高原东北缘地区噪声源表现出较强的季节性变化和能量优势方位分布特征,使得在研究该地区地下介质波速随时间的变化时不但需要考虑季节性特征带来的影响,而且特别是在用台站射线对时移方法研究介质波速变化时还需要考虑射线对方位的取向。
甘肃省地震局地震监测中心、青海省地震局地震监测中心和宁夏回族自治区地震局地震监测中心为本文提供了地震连续波形数据,在此一并表示感谢。
- 房立华,吴建平,吕作.2009.华北地区基于噪声的瑞利面波群速度层析成像[J].地球物理学报,52(3):663-671.
- 鲁来玉,何正勤,丁志峰,等.2009.华北科学探测台阵背景噪声特征分析[J].地球物理学报,52(10):2566-2572.
- 王伟涛,倪四道,王宝善.2011.云南地区地脉动噪声特征分析研究[J].地震,31(4):58-67.
- Bensen G.D.,Ritzwoller M.H.,Barmin M.P.,et al..2007.Processing seismic ambient noise data to obtain reliable broad-band surface wave dispersion measurements[J].Geophysical Journal International,169(3):1239-1260.doi:10.1111/j.1365-246X. 2007. 03374.x.
- Brenguier F.,Shapiro N.M.,Campillo M.,et al..2008.Towards forecasting volcanic eruptions using seismic noise[J].Nature Geoscience,1(2):126-130.doi:10.1038/ngeo104.
- Brooks L.A.,Townend J.,Gerstoft P.,et al..2009.Fundamental and higher-mode Rayleigh wave characteristics of ambient seismic noise in New Zealand[J].Geophysical Research Letters,36(23):doi:10.1029/2009GL040434.
- Derode A.,Larose E.,Tanter M.,et al..2003.Recovering the Green's function from field-field correlations in an open scattering medium[J].The Journal of the Acoustical Society of America,113(6):2973-2976.doi:10.1121/1.1570436
- Friedrich A.,Krüger F.,Klinge K..1998.Ocean-generated Microseismic Noise Located with the Gr Fenberg Array[J].Journal of Seismology,2(1):47-64.
- Kedar S.,Longuet-Higgins M.,Webb F.,et al..2008.The Origin of Deep Ocean Microseisms in the North Atlantic Ocean[J].Proceedings of the Royal Society A.,464(2091):777-793.doi:10.1098/rspa.2007.0277.
- Li H.,Su W.,Wang C.Y.,et al..2009.Ambient Noise Rayleigh Wave Tomography in Western Sichuan and Eastern Tibet[J].Earth and Planetary Science Letters,282(1-4),201-211.doi:10.1016/j.epsl.2009.03.021.
- Lin F.C.,Moschetti M.P.,Ritzwoller M.H..2008.Surface Wave Tomography of the Western United States from Ambient Seismic Noise:Rayleigh and Love Wave Phase Velocity Maps[J].Geophysical Journal International,173(1):281-298.doi:10.1111/j.1365-246X.2008.03720.x.
- Longuet-Higgins M.S..1950.A Theory of the Origin of Microseisms[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,243(857):1-35.doi:10.1098/rsta.1950.0012.
- Minato S.,Tsuji T.,Ohmi S.,et al.2012.Monitoring Seismic Velocity Change caused by the 2011 Tohoku-oki Earthquake using Ambient Noise Records[J].Geophysical Research Letters,39(9):doi:10.1029/2012GL051405.
- Pedersen H.A.,Krüger F..2007.Influence of the Seismic Noise Characteristics on Noise Correlations in the Baltic Shield[J].Geophysical Journal International,168(1):197-210.doi:10.1111/j.1365-246X. 2006.03177.x.
- Roux P.,Sabra K.G.,Kuperman W.A.,et al..2005.Ambient Noise Cross Correlation in Free Space:Theoretical Approach[J].The Journal of the Acoustical Society of America,117(1):79.doi:10.1121/1.1830673.
- Sabra K.G.,Gerstoft P.,Roux P.,et al.2005.Surface Wave Tomography from Microseisms in Southern California[J].Geophysical Research Letters,32(14):doi:10.1029/2005GL023155.
- Sabra K.G.2005.Extracting time-domain Green's Function Estimates from Ambient Seismic Noise[J].Geophysical Research Letters,32(3):doi:10.1029/2004gl021862
- Shapiro N. M.,Campillo M.,Stehly L.,et al..2005.High-resolution Surface-wave Tomography from Ambient Seismic Noise[J].Science,307(5715):1615-1618.doi:10.1126/science.1108339.
- Snieder R..2004.Extracting the Green's Function from the Correlation of Coda Waves:A Derivation based on Stationary Phase[J].Physical Review E,69(4):doi:10.1103/PhysRevE.69.046610.
- Stehly L.,Campillo M.,Shapiro N.M..2006.A Study of the Seismic Noise from its Long-range Correlation Properties[J].Journal of Geophysical Research,111(B10):doi:10.1029/2005jb004237.
- Wapenaar K.,Thorbecke J.,Draganov D..2004.Relations between Reflection and Transmission Responses of Three-dimensional Inhomogeneous Media[J].Geophysical Journal International,156(2):179-194.doi:10.1111/j.1365-246X.2003.02152.x.
- Weaver R.,Lobkis O..2001.Ultrasonics without a Source:Thermal Fluctuation Correlations at MHz Frequencies[J].Physical Review Letters,87(13):doi:10.1103/PhysRevLett.87.134301.
- Yang Y.,Ritzwoller M.H.,Levshin A.L.,et al..2007.Ambient Noise Rayleigh Wave Tomography Across Europe[J].Geophysical Journal International,168(1):259-274.doi:10.1111/j.1365-246X. 2006.03203.x.
- Yang Y.,Ritzwoller M.H..2008.Characteristics of Ambient Seismic Noise as a Source for Surface Wave Tomography[J].Geochemistry Geophysics Geosystems,9(2):doi:10.1029/2007GC001814.
- Yao H.,Van Der Hilst R.D.,De Hoop M.V..2006.Surface-wave Array Tomography in SE Tibet from Ambient Seismic Noise and two-station Analysis-I.Phase Velocity Maps[J].Geophysical Journal International,166(2):732-744.
- Zheng S.,Sun X.,Song X.,et al..2008.Surface Wave Tomography of China from Ambient Seismic Noise Correlation[J].Geochemistry,Geophysics,Geosystems,9(5):doi:10.1029/2008GC001981.
- Zheng Y.,Yang Y.,Ritzwoller M.H.,et al..2010.Crustal Structure of the Northeastern Tibetan Plateau,the Ordos block and the Sichuan basin from Ambient Noise Tomography[J].Earthquake Science,23(5):465-476.