基金项目:湖南省地震局2012年度地震科研课题项目(201201)资助.
(1.湖南省地震局,湖南 长沙 410004; 2.昆明峻奇无损检测工程有限公司,云南 昆明 650041; 3.昆明南方地球物理技术开发有限公司,云南 昆明 650091; 4.云南省地震局,云南 昆明 650224)
(1. Earthquake Administration of Hunan Province, Changsha 410004, Hunan, China)(2. Kunming JUNQI Inspection and Testing Engineer Co.,Ltd, Kunming 650041, Yunnan, China)(3. Kunming Southern Geophysical Technology Co.,Ltd,650091, Kunming, Yunnan, China)(4. Earthquake Administration of Yunnan Province, 650224, Kunming, Yunnan, China)
active block; strain energy; Bayan Har Terrane; Sichuan-Yunnan Rhombic Block; strong earthquake hazard area; Wenchuan MS8.0 earthquake
备注
基金项目:湖南省地震局2012年度地震科研课题项目(201201)资助.
综合地质构造、岩体力学性质、应力应变状态及其演化历史等各种因素将其统归为应变能积累特征对强震活动进行研究。对利用形变空间特征变化判断强震震源区位置的方法进行了讨论并确认其可行性,提出估算块体应变能的方法。由新构造划分块体边界、地壳测深确定底面进而确定块体体积、形变测量确定年平均应变速率、地壳速度构造确定弹性常数、历史强震确定能量积累起点(起始时间),由此估算块体积累总应变能,进而依据能量估算地震震级。最后以实例论述应变能积累特点对强震位置和震级预测的良好效果以及对地震安全性评价的重要意义。
Various factors such as geological structure, mechanics property of rock-mass, stress-strain state and its evolvement history etc. are boiled down to the characteristics of strain energy accumulation, and then the activity of strong earthquakes are studied. Firstly, we discussed the method which is used to judge the epicenter location of strong earthquake by spatial characteristic method of deformation and confirmed its feasibility, and proposed the method of estimating the strain energy in the geologic block. Secondly, on the basis of the block boundary is divided by new tectonic, the bottom is obtained by crustal sounding to determine the block volume,annual strain rate is achieved by deformation measurement, the elastic constant is acquired by crustal velocity structure, the energy accumulation point(starting time)is determined by use of historical earthquakes,we confirmed the total accumulation strain energy of the block, and predicted the magnitude of the future earthquake. Finally, we discussed the good effect of the features of strain energy accumulation on predicting the location and magnitude of strong earthquakes, and the significant role in earthquake safety evaluation by real examples.
引言
地震安全性评价的一个重要内容是确定潜在震源区的位置及最大震级,这直接影响抗震设防要求的确定。设防过高,将使工程造价猛增; 设防偏低,将会付出惨痛的代价。《工程场地地震安全性评价》(GB17741—2005)为工程场地地震安全性评价制定了一系列原则、标准和方法,其中规定了如何利用构造地质、大地形变测量、地球物理场以及历史地震等进行研究。以往研究多分别用地应力或应变(形变)进行地震预测研究,很少有人进行综合考虑。理论及实验研究显示,潜在震源区的位置和最大震级不仅与构造和历史地震有关,更与应力状态,包括方向、大小、增加速率、集中位置等,以及岩体自身性质,包括强度、杨氏模量、应变大小及增长速率、裂缝(断层)大小和数量等有关,同时还与作用方式有关。许昭永等(2010)综合各种因素,将其统归为一个物理量——应变能积累释放特征进行初步研究。陈祖安等(2009)以应变能密度的空间分布讨论2008年汶川8.0级地震孕震机理。本文将进一步以实例论述如何简便准确地计算活动块体应变能,并将其应用于潜在强震区及其最大震级的预测研究。
1 应变能密度及破裂判据
2 关于强震位置和震级的预测方法
3 实际震例、资料分析
4 讨论和结论
4.1 以应变能预测强震震级和位置的可行性及意义以形变的空间分布特征预测强震危险区(潜在震源区)方法比较成熟,可以直接使用,只是还需对它的唯一性进行研究,即如何确定强震在哪一个危险区中发生。
本文是对整个活动块体上可能发生强震的最大震级预测,而并非对特定地点进行预测,由于目前还没有满足(1)式精确计算块体应变能的条件,与其它定量地学问题一样,在估算应变能积累总量时,本文也作了诸多简化假设。这可能使
表1 东南块体M≥7强震与用能量积累释放曲线预测震级的比较
Tab.1 The comparison of M≥7 strong earthquakes and magnitude predicted by energy accumulation and releasing curve in southeast of Sichuan-Yunnan Rhombic Block结果具有很大的不确定性,然而依然可满足对最大震级判定的精度要求。因为其它方法所得结果的偏差很难小于10%,而对于震级预测,能量即使偏差30%,震级偏差只有0.3级; 能量偏差10倍,震级偏差也只有0.7级。因此,用本方法虽然有一定的不确定性,但从所列震例看,以块体应变能预测强震震级与实际震级是吻合的。比如汶川地震和川滇菱形块体东南块体强震预测结果,与实际震级偏差都小于0.5级,可满足地震安全性评价对潜在地震最大震级预测的精度要求,而相应的计算条件及工作量却简化得多。当然在资料足够和条件许可时,也可尽量逼近(1)式去计算块体应变能。
因此,本文方法预测强震震级是可行的,至少不会比实际震级低太多。它对地震安全性评价可能很有意义,可避免使抗震设防烈度偏离实际太多。
4.2 块体应变能积累释放周期和强震活动如前文所述和图3所示,川滇菱形块体的东南块体应变能有完整的积累释放周期。它完全不同于传统的应变释放曲线,既包含了强震应变能释放,也包含了块体总应变能的增长。比较完整的周期有两个,大约都为120年。其共同特点为:一个新周期开始,大约有30年不会发生M≥7强震,即相对平静期。随时间推移,两个周期内都多次发生M>7地震,直到发生M≥7.5地震释放绝大部分能量为止,而后新的周期开始。发生强震的这一时期为活跃期。前后两个周期的地震活跃期大约都为90年。
以活动块体应变能周期积累释放来讨论强震活动,其物理意义非常明确。它类似于完整岩石破坏试验和粘滑试验应变能随时间的变化。在加载前期,应力、应变随时间增加,则应变能随时间增加。但由于这一时期,块体内总应变能较低,虽然在块体边缘或内部断层端部也有一些应力集中的地方,但由于积存能量较少,因此没有发生M≥7强震,这一时期为平静期。随着时间增长,应变能持续增加。在块体的多个应力集中部位,先后达到发生强震的条件,如应变能密度因子达到或超过临界值,并且也已积累了足够的能量即发生强震。但这个地震是在应变能的上升积累期发生的,一次强震只是释放了一部分能量,随着时间推移,应变能继续增长。于是就形成了锯齿形起伏增长曲线。直到周期末尾,以一、二次特大强震将绝大部分应变能释放而结束。另外,对于同一地质块体来讲,其力学性质随时间变化相对较小,但所受荷载速率绝不像我们所假设的那样大小均匀。因此,要积累到相同极大强震(如8级)的能量,其所需时间也就不尽相同。这就是虽有积累释放周期特征,但各周期并不完全相同的原因。对于不同块体,其力学性质不同,应力速率不同,其积累到极强震所需能量的时间(应变能积累释放周期)就更不可能相同了。
在论及地震活动周期时,都是对某一地域的强震在时间域上的重复出现间隔。而笔者研究发现,对一个固定活动块体,其所能够积累的应变能是有限的,在达到一定大小后,就会一边积累,一边释放(部分先期强震),只是积累比释放多; 在达到它所能承受的极限后,将以极强震形式(一个或两个)释放大部分能量,而后重新再积累、再释放,如此形成地震平静—活跃循环周期。但它绝不是单个地震的重复发生周期。如图3所示,强震在时间上没有任何规律。只是随着时间增长,应变能迅速增长,可能发生的最大地震震级加大而已。由此得到重要启示:以整个块体应变能的积累释放周期特征来研究强震活动,可能更有意义。然而这种应变能积累释放周期和强震活动的关联研究还太少,这种地震平静—活跃循环周期对各个活动块体是否都成立,也还不能确定。如2010年4月青海玉树7.1级、2013年4月四川芦山7.0级地震在巴颜喀拉地块东部,都在四川汶川8级地震之后,这与川滇菱形块体东南块体上云南嵩明8级地震以后再发生四川西昌普格7.5级地震相似,可能是前一周期的结束,后一周期的开始。而2014年2月新疆于田7.3级在巴颜喀拉地块西部,资料更为缺乏,因此对此块体应变能积累释放周期和强震活动以及相关问题还需另行研究。
4.3 多块体活动的相互影响2008年汶川8.0级地震,其预测震级为7.8级,1833年云南嵩明8级地震,其预测震级为7.7级,引起震级差的原因很多,其中一个重要因素是未将相邻块体(如华南块体)积累的应变能进行累加。如1996年2月3日云南丽江7级地震,发生在川滇菱形块体东南和西北两个块体的交界处。到1996年西北块体已积累应变能1015.93 J,东南块体已积累应变能1016.08 J,单用一个块体积累的应变能计算都达不到发生7级地震的条件,但两者相加应变能积累达1016.31 J,就足以形成7级地震。另外的最大影响因素可能是当年的应变速率比现在大。因此在预测块体交界处的强震震级时一定要将相邻块体积累的应变能进行累加。
在相邻块体发生强震后将引起本块体的应力调整,可能使本块体积累的应变能减少或改变积累速率,因此可能推迟或加速本块体强震的发生。这就是说,在预测某一块体强震活动时,除研究本块体应变能积累释放特征外,还必须注意相邻块体的影响。
4.4 需要进一步研究的问题上述方法只是一种探讨,还需要深入研究和改进。一是计算条件,如块体应变能密度不可能处处均匀相等,应力、应变速率也不会永远为常数,所用应变速率并非本块体实测,深部应力、应变状态未必与地表一致等。主轴方向的应变能严格说不能只以杨氏模量和应变速率计算,3对(6个)剪切应变能差异较大。再者研究实例太少,有许多问题待解,如块体应变能积累释放周期是否普遍,其影响因素如何,如何对具体单一危险区确定最大震级等。诸如此类的问题有待进一步完善研究。
4.5 结论综上所述,将应力、变形、深部构造、大地构造、历史地震等多方面因素综合为应变能一个物理量,以此活动地块的应变能确定潜在震源区及其最大震级是有益的,它不致于漏下强震。这可能对地震安全性评价非常重要。但此种研究刚刚开始,要达到应用还需深入研究。
- 陈章立,赵翠萍,王勤彩,等.2009.汶川MS8.0地震发生背景与过程的研究[J].地球物理学报,52(2):455-463.
- 陈祖安,林邦慧,白武明,等.2009.2008年汶川8.0级地震孕震机理研究[J].地球物理学报,52(2):408-417.
- 郭良迁,李延兴,胡新康,等.2009.中国大陆地壳运动与汶川MS8.0级地震孕育的关系[J].地球物理学报,52(2):531-537.
- 皇甫岗,陈颙,秦嘉政,等.2010.云南地震活动性[M].昆明:云南科技出版社,23-30,108.
- 黄永祥,黄润秋,许强,等.2002.昆明玉溪研究区GPS 和Kaiser应力测量结果与数值拟合反演[J].地震研究,25(增刊A):48-56.
- 江在森,方颖,武艳强,等.2009.汶川8.0级地震前区域地壳运动与变形动态过程[J].地球物理学报,52(2):505-518.
- 阚荣举,林中洋.1986.云南地壳上地幔的初步研究[J].中国地震,2(4):50-61
- 李延兴,郭良迁.2002.昆明及其邻区的地震活动趋势估计[J].地震研究,25(增刊A):12-16.
- 李延兴,张静华,周伟,等.2009.汶川MS8.0地震孕育发生的机制与动力学问题[J].地球物理学报,52(2):519-530.
- 刘启元,李昱,陈九辉,等.2009.汶川MS8.0地震:地壳上地幔S 波速度结构的初步研究[J].地球物理学报,52(2):309-319.
- 梅世蓉,薛艳,宋治平.2009.汶川8.0级与昆仑山口西8.1级地震前地震活动异常特征与启示[J].地震,29(1):1-14.
- 王椿槦,吴建平,楼海,等.2003.川西藏东地区的地壳P波速度结构[J].中国科学(D辑),33(增刊):181-189.
- 王椿槦,王溪莉,颜其中.1994.昆明地震台网下方的三维速度结构[J].地震学报,16(2):167-175.
- 闻学泽,张培震,杜方,等.2009.2008年汶川8.0级地震发生的历史与现今地震活动背景[J].地球物理学报,52(2):444-454.
- 许昭永,胡毅力,许峻,等.2010.应变能积累在地震安全性评价中的应用探讨[J].地震学报,32(1):77-87.
- 薛艳,刘杰,梅世蓉,等.2009.2008年汶川MS8.0地震前地震活动异常特征[J].地震学报,31(6):606-619.
- 尹祥础.2011.固体力学[M].北京:地震出版社,58-65,388-427.
- 张培震,邓起东,张国民.2003.中国大陆的强震活动与活动地块[J].中国科学(D辑),33(增刊):12-19.
- 张培震,徐锡伟,闻学泽,等,2008.2008年汶川8.0级地震发震断裂的滑动速率、复发周期和构造成因[J].地球物理学报,51(4):1066-1073.
- 周永胜,何昌荣.2009.汶川地震区的流变结构与发震高角度逆断层滑动的力学条件[J].地球物理学报,52(2):474-484.
- Gutenberg B.,Richiter C.F..1956.Earthquake magnitude,intensity,energy,and acceleration[J].Bull.Seism.Soc.Am.,46(2):105-143.
- Kanamori H.,黄辅琼.2003.地震的能量收支与地震效率[J].世界地震译丛,(5):61-68.
- GB17741—2005,工程场地地震安全性评价[S].
3.1 汶川地震汶川地震位于巴颜喀拉块体与华南块体交界处。下文以巴颜喀拉块体应变能进行探讨。
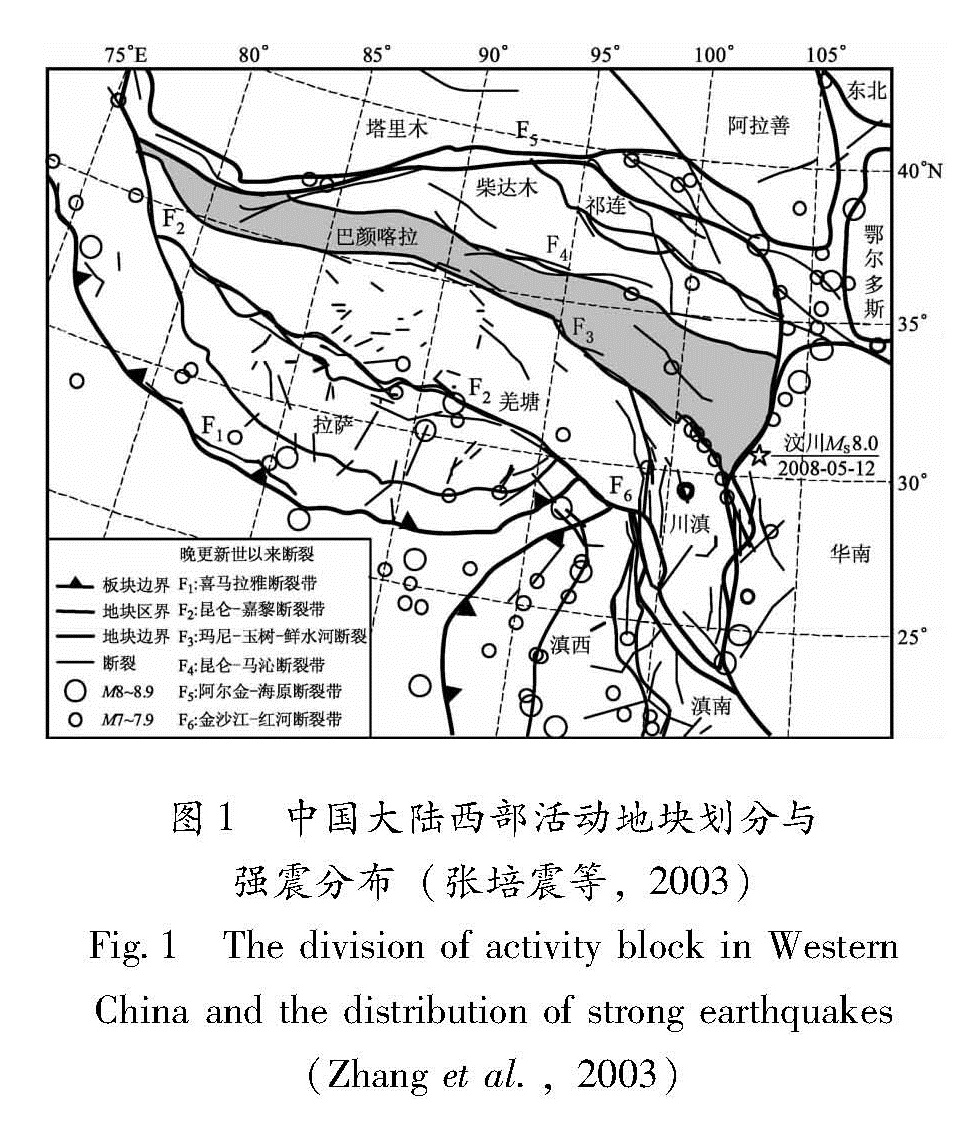
3.1.1 应变能积累体积图1 中国大陆西部活动地块划分与强震分布(张培震等,2003)
Fig.1 The division of activity block in Western China and the distribution of strong earthquakes(Zhang et al.,2003)依据张培震等(2003)的研究结果(图1),取巴颜喀拉块体为积累应变能主块体,其边界为图中阴影区所示,块体地表面积取几个梯形计算。刘启元等(2009)研究结果表明,松潘—甘孜地块地壳厚度由西侧靠近鲜水河断裂的60 km,向东减为52 km,取平均厚度为56 km计算块体体积。
在78°~90°E范围: V1=1.20×1016 m3; 在90°~105°E: V2 =2.548×1016 m3; V=V1+V2=3.748×1016 m3。
3.1.2 弹性常数据刘启元等(2009)关于31°N线地壳上地幔S波速度构造剖面,龙门山断裂西侧、鲜水河断裂东侧深度25~30 km处横波速度为3.60 km/s。王椿槦等(2003)关于30°N线地壳上地幔P波速度构造剖面,龙门山断裂西侧及鲜水河断裂东侧深度25~30 km处纵波速度为6.25 km/s,密度都为2.70×103 kg/m3。巴颜喀拉地块(龙门山断裂以西、鲜水河断裂东)深度25~30 km处剪切模量μ=3.499×1010 Pa、泊松比ν=0.252,杨氏模量E=8.762×1010 Pa。
3.1.3 年平均应变速率由巴颜喀拉地块上不同地区和四川盆地应变场的平均主应变参数与震中区在各时段的主应变参数(李延兴等,2009)可知,在1999~2007年,主张应变由西(93.5°E)向东(105.5°E)逐步减小,主压应变变化不大。震中区主压应变明显增大,主张应变也有所回升。对于本文讨论问题,取最大值。参照江在森等(2009)、郭良迁等(2009)的结果,1999~2007年巴颜喀拉块体在93.5°~95.5°E区域,平均主压应变、主张应变及剪应变速率都达到最大值,分别为2.0843×10-8/a、6.1848×10-8/a、8.5×10-8/a。
3.1.4 能量积累起始时间依据闻学泽等(2009)对(99°~108°E,27°~35°N)范围内历史地震分布的分析,并参照张培震等(2008)的研究,巴颜喀拉块体(包括块体边缘和块内)近400年内M≥7地震约为20次。从已有的资料看,巴颜喀拉块体东部边缘龙门山断裂北部(松潘—茂县间),1713年曾发生7级地震,1933年又发生71/2级地震。依据前述原则,取1933年作为块体应变能积累的起始时间。
3.1.5 能量积累依据式(12)、(13)计算应变能积累:
W=Vw=4.355×1013T2.(18)
从1933年松潘—茂县间71/2级地震到1976年松潘—平武7.2级的44年,应变能为1×1016.93。从1933年地震到2008年汶川8.0级地震的75年间,应变能为1×1017.39,扣除1976年松潘—平武地震已释放的能量,实际积累应变能为1×1017.15。
3.1.6 震级上限的确定依据式(16)由应变能积累确定震级上限,从1933年松潘—茂县间71/2级到1976年松潘—平武7.2级地震的巴颜喀拉块体应变能估算震级为M=7.54。从1933年松潘—茂县间71/2级地震到2008年汶川8.0级地震时的巴颜客拉块体积累的应变能估算震级为7.85,扣除1976年松潘—平武地震已释放的能量,预估震级为7.69。
3.2 川滇菱形块体东南块体应变能积累和强地震活动3.2.1 块体体积川滇菱形块体被羌塘、巴颜喀拉、华南、滇南和滇西块体包围。其北边、东边边界由鲜水河、安宁河、则木河和小江断裂构成,西边、南边
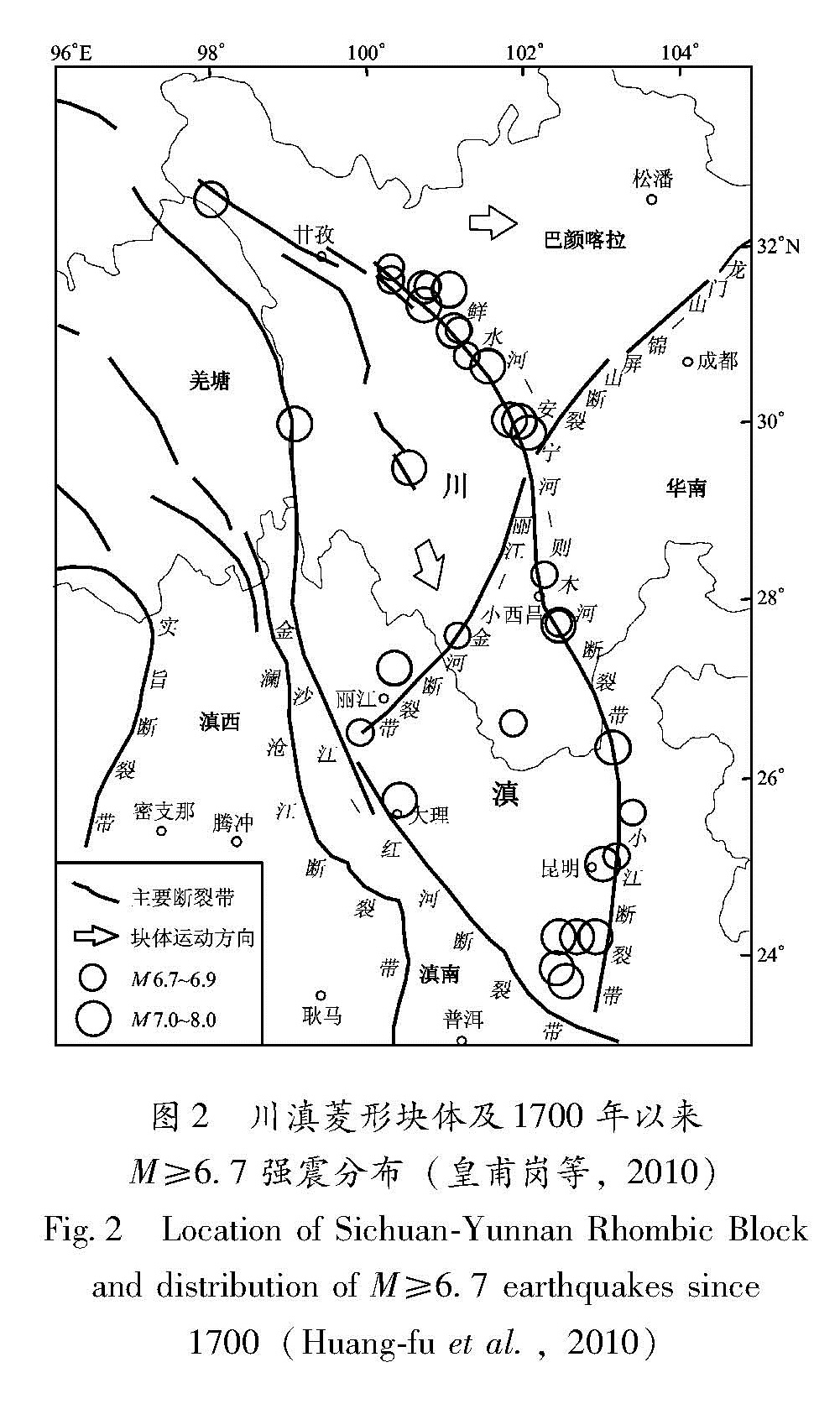
边界由红河断裂构成。面积约26×104 km2(图2)。川滇菱形块体地壳厚度北厚南薄,在丽江—小金河断裂带附近厚度梯度变化较大。皇甫岗等(2010)以此断裂带将菱形块体分为西北和东南两块。东南块体厚度较小,约38~48 km,平均43 km。东南块体面积约1.16×1011 m2,体积约4.99×1015 m3。图2 川滇菱形块体及1700年以来M≥6.7强震分布(皇甫岗等,2010)
Fig.2 Location of Sichuan-Yunnan Rhombic Block and distribution of M≥6.7 earthquakes since 1700(Huang-fu et al.,2010)3.2.2 块体弹性常数黄永祥等(2002)曾利用阚荣举和林中洋(1986)、王椿槦等(1994)关于滇中地壳的速度构造结果,计算川滇块体东南块体的3个地区的杨氏模量,分别为6.98×1010 、2.80×1010 和7.74×1010 Pa。其中较低者为断层带附近所得,块体内部杨氏模量较高。本文取川滇块体东南块体的杨氏模量E=7.74×1010 Pa,剪切模量μ=3.173×1010 Pa。
3.2.3 应变速率在1970年通海地震和1973年炉霍地震前并无本地块相关形变数据,于是取近年来川滇菱形块体和邻近块体的主张应变、主压应变和剪应变的平均年应变速率进行研究。依据李延兴和郭良迁(2002)测得的昆明及邻区主压应变、面应变和最大剪应变等值线图,将1999~2001年昆明南平均年速率主压应变1.1×10-7/a、主张应变1.0×10-7/a(取值与面应变同)和剪应变1.5×10-7/a分别作为东南块体的主压、主张和剪应变速率。
3.2.4 应变能积累川滇菱形块体东南块体的应变能积累为
WSE=1.886×(Δt)2×1013.(19)
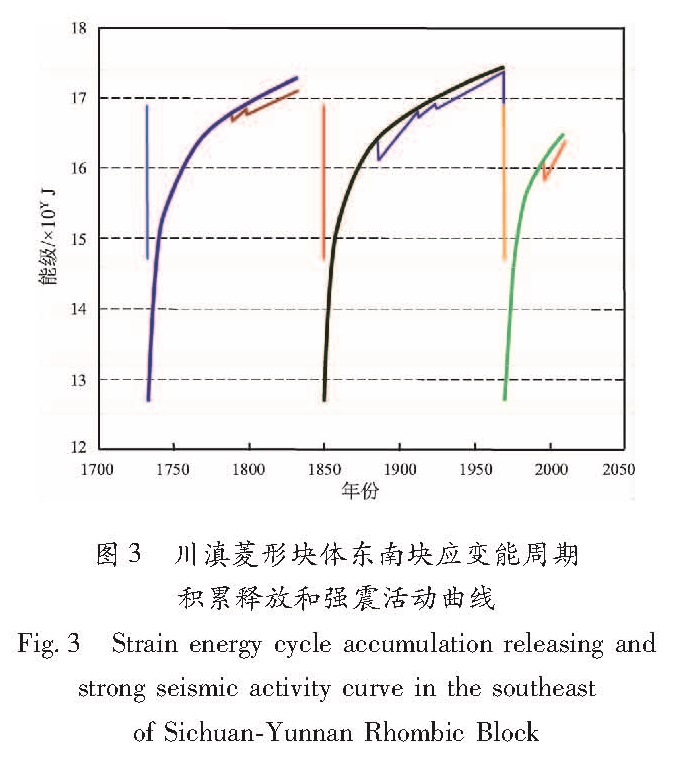
3.2.5 应变能积累释放周期和强震活动特征1700年以来,东南块体M≥7.5地震有4次:1733年云南东川紫牛坡71/2级,1833年云南嵩明8级、1850年四川西昌普格间71/2级和1970年云南通海7.8级。按前述原则,第一周期从1733年起始。由于嵩明8级和西昌普格间71/2级地震仅相隔17年,为确保新周期开始后其前一周期的应变能绝大部分或完全释放,因此,第二周期起始点取四川西昌普格间71/2级地震的发生时间为零点。由式(19)得到,东南块体全部应变能积累随时间增长的平滑曲线(图3),由式(17)得到包含每次强地震能量释放及其后应变能重新积累的锯齿
形增长曲线。图3 川滇菱形块体东南块应变能周期
积累释放和强震活动曲线
Fig.3 Strain energy cycle accumulation releasing and strong seismic activity curve in the southeast of Sichuan-Yunnan Rhombic Block从图3可看出块体应变能积累具有明显的特征:
(1)块体应变能积累释放具有周期性。释放周期比较完整的有两个,大约都为120年。1733年东川紫牛坡强震之前为一个不完整周期。第一周期以1733年为起始,1850年结束,紧接着第二个周期开始。1970年云南通海7.8级地震发生,第二周期结束,第三周期开始。从图3看出,从一个新周期开始,大约有20年左右或更长时间不会发生M≥6.7强震,30年左右不会发生M≥7强震。
(2)120年积累的应变能为1×1017.43 J,预测
强震为7.87级。然而,这些应变能是由几个强震释放的,其中M≥7地震有4次。
(3)每个周期中,M≥7强震之后到下一个强震时块体所积累的应变能,都不足以形成后一个强震。然而,从周期开始到每个强震发生,块体积累的应变能,包括扣除已发生强震所消耗的能量,都足以形成本次强震。
(4)第二个周期应变能积累释放曲线显示,每次强震时的预测震级,都高于实际发生的强震,仅1970年的强震预测震级与实际震级相同(表1)。而对于第一周期,前两次的预测震级高于实际强震,但对1833年的嵩明8级强震预测震级仅为7.7级。
(5)这些强震在时间上没有规律,只是随着时间增长,应变能迅速增长,可能发生的最大地震震级也会加大。
2.1 潜在震源区位置预测发震位置预测,有多种方法可行。如梅世蓉等(2009)、薛艳等(2009)和陈章立等(2009)就以中强地震的时空活动特征确定汶川地震的发震位置,李延兴等(2009)则认为汶川地震发生在剪切应变高梯度变化区。笔者更倾向以现代形变特征区确定强震位置。强震前会出现一系列地形变方面的特征变化,强震就发生在应变集中区或高应变梯度区(或其附近)。但往往有几个应变集中区或高应变梯度区,究竟哪个区先发生强震需另行研究(李延兴,郭良迁,2002)。这方面资料很多,且技术较为成熟(许昭永等,2010),本文不再赘述。
利用形变场的空间特征判定强震发生位置直观、简便,因此本文并不强调用应变能密度的空间分布来判定强震位置。
2.2 潜在强震震级预测上述几种理论计算并非都能运用于实际观测中。为方便准确的利用(1)~(3)式估算块体应变能,这里再作几项假定:
(1)应力及应变速率都为常数,并且应力和应变速率也为线性关系:
dσij/dt=2μdεij/dt+λ(d/dt)δij.(10)
设初始应力、应变为零,于是在时间T后,应力为
σij=2μεij+λδij
=2μ∫T∫0(dεij/dt)dt+λ∫T∫0((d/dt)δij)dt
=(2μ(dεij/dt)+λ(d/dt)δij)T.(11)
(2)块体内应变能密度均匀分布。块体体积为V,于是(1)式简化为
W=Vw.(12)
(3)以单一形式分别计算各部分应变能,而后再迭加。
从式(2)、(3)可看出,应变能包括两部分:体积应变能3项,剪切应变能6项。理论上只要测得3个主应变方向的应变,其它6个(3对)剪应变都可由此导出。实际测量时经常给出两个方向的主应变(最小和最大主应变),因此仅能得到一个(一对)最大剪应变。平均两个方向的伸缩应变能,再乘以3得到体积变形总应变能密度。以一个最大剪应变能密度乘以3.5得到剪切总应变能密度。这是因为中间主应变居于最小和最大主应变之间:它若趋近最小和最大主应变的平均值,则剩余4个(两对)剪切变形应变能(密度)总和恰好等于一个前述最大剪应变能(密度); 若趋近最小或最大主应变,则剩余4个(两对)剪切变形应变能(密度)总和恰好等于两个前述最大剪应变能(密度); 故取平均以一个最大剪应变能(密度)乘以3.5得到剪切总应变能(密度)
于是,将体积变形和剪切应变相加可粗略地得到总应变能密度:
w=[3(λ+2μ)(ε211+ε133)/2+3.5×2με213]/2
=[3E((dε11/dt)2+(dε33/dt)2)/2+3.5×2μ(dε13/dt)2]T2/2.(13)
2.2.1 年平均应变率的测定许昭永等(2010)、张培震等(2008)的研究表明,由地震地质方法所得的结果与GPS技术实测结果非常接近。因此,块体的应变速率一般应由GPS测定,在资料缺乏时,也可由地质资料推断。
2.2.2 弹性常数的确定用应力应变测量结果估算应变能密度比较直接,但现今应力测量依然较难。因此可采用地壳测深结果由纵、横波速度估测弹性常数。由下式计算拉梅常数λ、剪切模量μ,进而可得出其它各弹性常数:体积模量K、泊松比ν以及杨氏模量E。
V2S=μ/ρ; V2P=(λ+2μ)/ρ,
V2ε/(V2P-V2S)=μ/(λ+μ)=1-2v.(14)
其中,v,ρ分别为泊松比和密度。
E=2μ(1+v).(15)
随深度增加,(围)压力升高,温度增加。前者使岩体强度增加,后者使强度降低。参照周永胜和何昌荣(2009)的研究结果,在25 km深度附近,强度最高。所以,取25 km深度附近的波速确定弹性常数。
2.2.3 应变能积累的零点或起始时间的确定经过一些对比研究,我们依据历史强震资料,取某次特大地震(M≥7.5)的发生时间为后续应变能积累的起始时间。若这一时期连续有2个M≥7.5强震,则取后一个为后续应变能积累周期的起始时间。这样能确保这次强震后,前一周期的应变能基本释放完。当然,这并非是真正零点,还有一定程度的应力和应变能,但重新积聚的应变能必须高于此值才可能再发生地震,而且在发生强震时的应变比初始值高几个数量级,因此可将初始应变设为零,于是由(13)式估算应变能密度。我国历史强震资料丰富,对于许多活动块体,都可以比较容易地确定应变能积累释放周期的起始时间。
2.2.4 块体体积及应变能的确定对大的地块,采用张培震等(2003)关于活动地块的定义和方法划分; 相对小一些的用地震安全性评价中的Ⅱ、III级构造来划分块体。这种块体不易太小,其边界应有明确的界限特征。而块体内可能还存在并未贯穿整个块体的断层。块体底面以地壳底面为界,由此估测积累应变能的体积。
对于块体应变能的计算,若在块体内部,则以一个整块体估算; 若在块体交界处,则应将相邻几个块体积累的应变能进行累加。
对于含有断层的块体,依据断层将相邻各部分划成几个块体,迭加各块体应变能,求出总应变能。
2.2.5 震级上限的确定地震时转换成地震波的能量与震级有经验关系(Gutenberg,Richiter,1956):
lgWB=4.8+1.5M.(16a)
然而,地震波释放的能量占总应变能量的比例(即地震效率)至今还没有定论。但有许多研究结果,如Kanamori和黄辅琼(2003)认为,地震效率大约为百分之几到百分之十几,其上限为18%。本文用总能量的15%估算震级(能量单位为焦耳),代入式(16)得
lgW=5.624+1.5M.(16b)
2.2.6 包含强震释放的应变能积累研究表明,到某次强震时,块体应变能并非单调增长,而是此前还有强震发生即已释放部分应变能,以下式计算实际应变能积累:
W=Wts-∑n-11Wti.(17)
式中,Wts为到t时的块体应变能积累,由式(2)、(3)、(12)、(13)计算,Wti为t时之前各个强震所释放的应变能,由(16)式计算。
依据尹祥础(2011)固体力学的论述,块体应变能(积累)
W=w(x,y,z; t)dvdt.(1)
其中,w(x,y,z; t)为应变能密度,它与块体的空间位置及时间变化有关,应变能W的大小还与块体体积及积累时间长短有关。
1.1 应变能密度1.1.1 完整块体应变能密度对于线弹性体,应变能密度为
w=1/2σijεij, i,j =1,2,3.(2)
由广义胡克定律得知
σij=2μεij+λδij(3)
当i=j时,δij=1; 当i≠j时,δij=0。
1.1.2 含断层(裂缝)块体应变能密度设KⅠ、KⅡ、KⅢ分别为Ⅰ、Ⅱ、Ⅲ型应力强度因子,则
KⅠ=σ∞(πa)1/2,KⅡ=τ∞xy(πa)1/2,KⅢ=τ∞(πa)1/2.(4)
式中,σ∞、τ∞xy、τ∞分别为无穷远处的拉(正)应力、剪应力及撕剪应力,a为裂缝半长度。对于三轴应力作用时,σ∞、τ∞xy、τ∞可由σ1、σ2、σ3导出。
对于复合型裂纹,端部各点的应变能密度为
w=S/r=(α11K2I+2α12KⅠKⅡ+α22K2Ⅱ+α33K2Ⅲ)/r.(5)
其中,S为应变能密度因子,S=S(θ)。r为到达裂缝端点的距离,θ为r与裂缝延长线的夹角。αij为与剪切模量μ、泊松比ν及角度θ有关的常数。
1.2 破裂判据最简单的判据就是当K≥KC时,裂纹开始失稳扩展(破裂)。KC为断裂韧性,是材料的一个重要参数,表示裂纹开始失稳扩展时应力强度因子的临界值。
更常用的破裂判据是应变能密度因子和能量释放率,二者其实是一致的,只是表述方式不同。应变能密度因子准则认为,裂纹沿最小应变能密度因子Smin的方向扩展,即沿满足条件
(S)/(θ)=0,(2S)/(θ2)>0.(6)
的方向扩展; 当Smin达到一定的临界值SC时,裂纹开始失稳扩展。即
Smin=S(θ0)=SC.(7)
对于完整岩石的剪切破坏,一般用库仑准则,其也适用于塑性破坏,或用于判定结构体沿软弱面滑动破坏。
τ=C+σtgφ.(8)
式中,C、φ分别为内聚力和内摩檫角。
对于三轴应力,在平面应力时,
C=-(σ1+σ3)/2tgφ+(σ1-σ3)/2(sin2α-tgφcos2α).(9)
参照应变能密度因子判据和最大能量释放率准则,当所积累应变能密度达到或超过块体同一区域材料所能承受的极限(临界)值时,即发生局部破坏或破裂(地震)。