地震研究

统计分析了汶川地震滑坡在不同影响因子下数量和密度,然后采用归一化方法确定影响地震滑坡的关键因子。基于关键因子建立了地震滑坡密度数学模型。结果表明:从滑坡数量看,滑坡主要集中在(10°～20°)至(40°～50°)的坡度(90 m栅格)区间,主体集中在35°附近,在3°～7°之间有一个滑坡分布的小峰值; 滑坡密度随着坡度的增加而增加,在3°～7°的低坡地带有一个滑坡密度小峰值,在坡度一定的情况下,除了烈度外,其他影响因子下滑坡密度并没有表现出足够明显的规律性变化; 归一化计算结果表明:坡度和烈度是地震滑坡的关键因子; 根据逻辑斯蒂模型计算的结果,将地震滑坡危险性分为几无(≤0.01)、轻微(0.01～0.03)、中等(0.03～0.09)、严重(0.09～0.27)、特重(≥0.27)5个等级。地震滑坡危险性预测数据在鲁甸地震等地震应急中发挥了较好作用。

In order to quickly and accurately predict the risk of earthquake induced landslides after the earthquake,we count and analyze the quantity and the density(which means the number of the landslide per unit area)of Wenchuan M_S8.0 earthquake induced landslides in different impact factor,and determine the key factors of earthquake induced landslides by normalization method. Then based on the key factors,we develop a mathematical model for the earthquake induced landslides frequency.Taking the landslides number as the main statistical standards,we find that the landslides are mainly concentrated in the slope of 10-20°～40-50°(based on the grid of 90 m),most landslides are concentrated in the slope of 35° and its nearby,and there is a small peak with landslides distribution in the slope of 3°～7°. The density of landslides increases with the increase of the slope,and there is a small peak of landslides density during the slope of 3°～7°. If the slope remains unchanged,we find that landslides density do not show a regular variation with other factors except intensity. The normalized calculation results show that the slope and the intensity are the key factors of earthquake induced landslides.According to the calculation result of Logistic model,we divide the risk of earthquake induced landslides into 5 grades:Few(≤0.01),Low(0.01～0.03),Medium(0.03～0.09),Critical(0.09～0.27)and Extra-heavy(≥0.27). Now,the predicting data of the risk of earthquake induced landslides has played a good role in Ludian M6.5 earthquake emergency.

引言
1 数据和方法
2 地震滑坡影响因子分析
3 地震滑坡危险性模型
4 地震滑坡危险性评估模型初步应用
5 结论和讨论

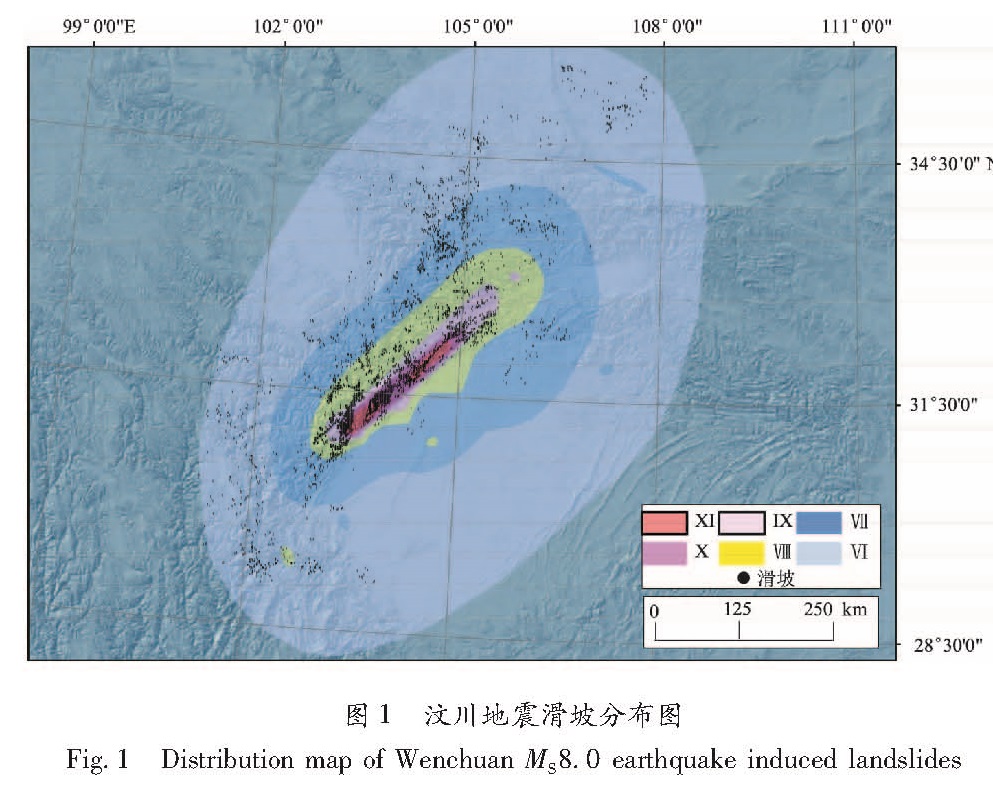
图1 汶川地震滑坡分布图<br/>Fig.1 Distribution map of Wenchuan MS8.0 earthquake induced landslides

图1 汶川地震滑坡分布图
Fig.1 Distribution map of Wenchuan MS8.0 earthquake induced landslides

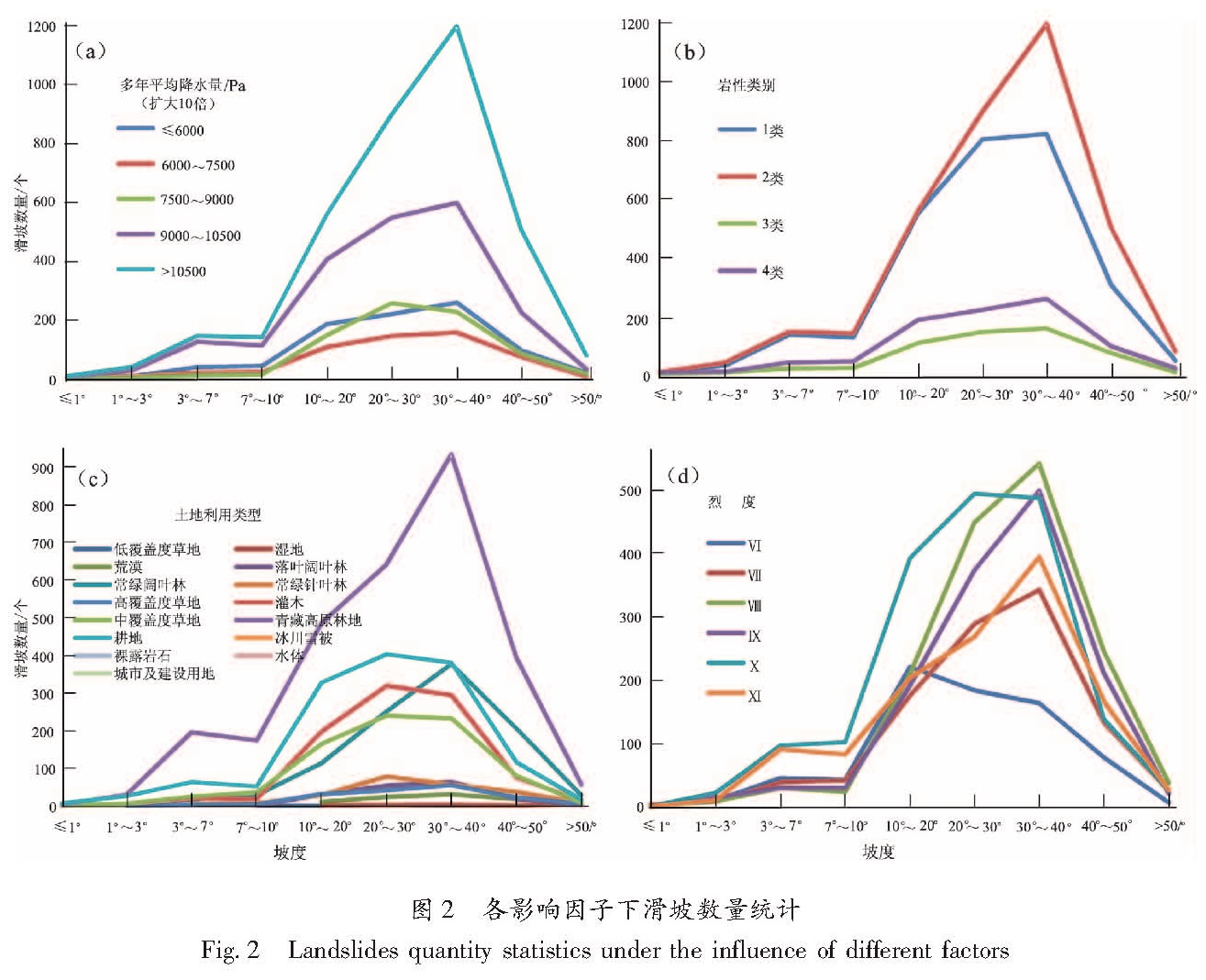
图2 各影响因子下滑坡数量统计<br/>Fig.2 Landslides quantity statistics under the influence of different factors

图2 各影响因子下滑坡数量统计
Fig.2 Landslides quantity statistics under the influence of different factors

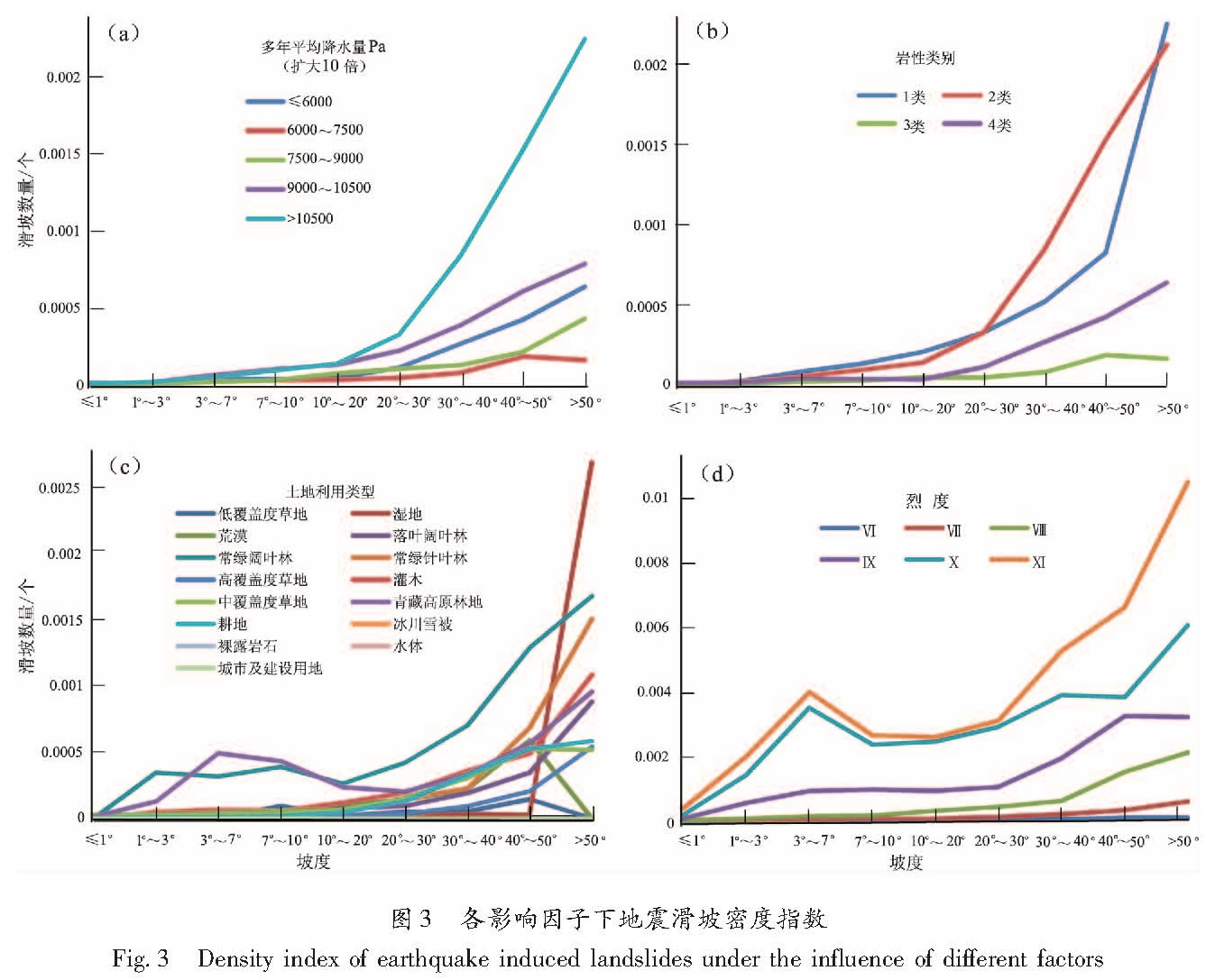
图3 各影响因子下地震滑坡密度指数<br/>Fig.3 Density index of earthquake induced landslides under the influence of different factors

图3 各影响因子下地震滑坡密度指数
Fig.3 Density index of earthquake induced landslides under the influence of different factors

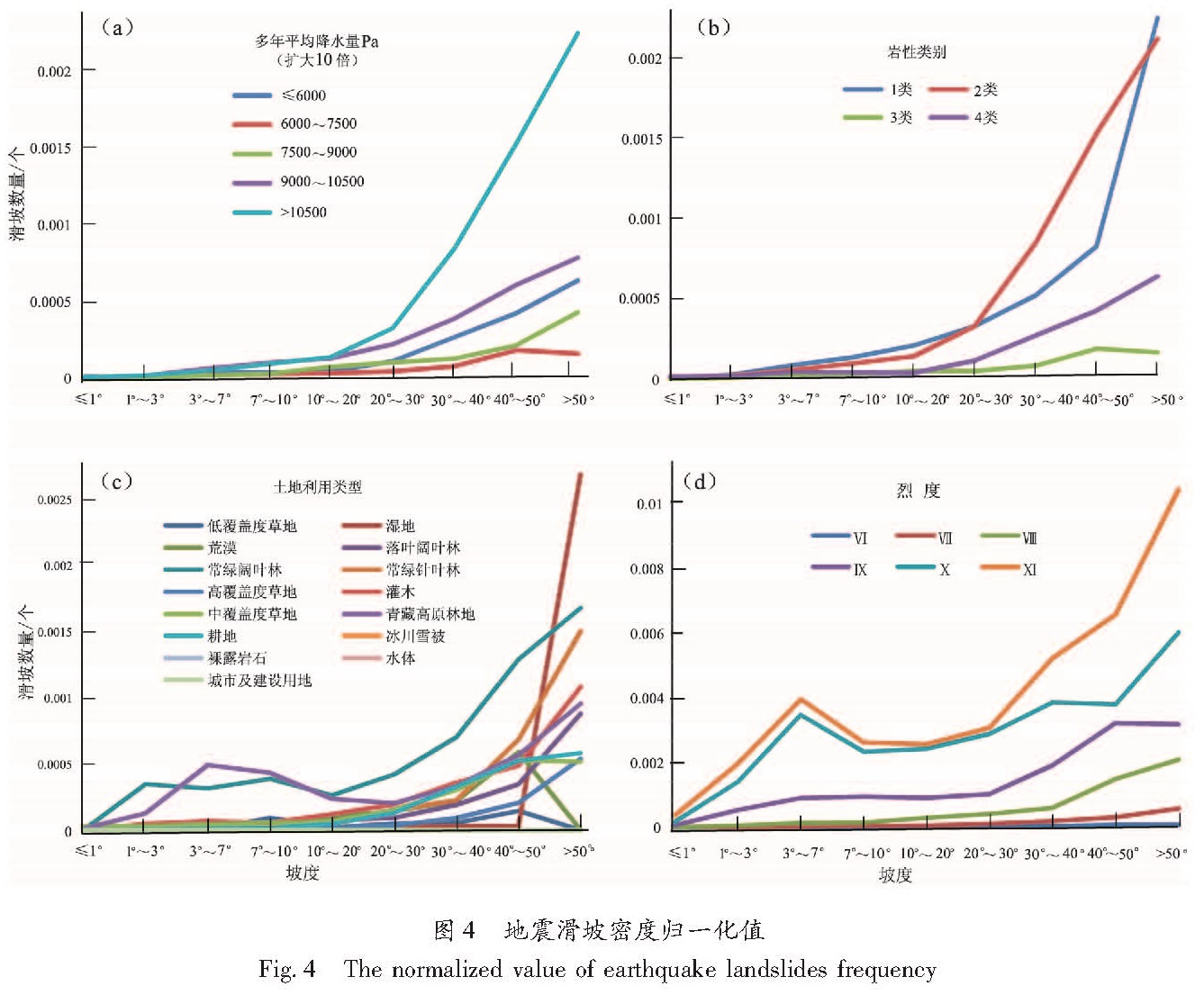
图4 地震滑坡密度归一化值<br/>Fig.4 The normalized value of earthquake landslides frequency

图4 地震滑坡密度归一化值
Fig.4 The normalized value of earthquake landslides frequency

表1 不同坡度下的地震滑坡密度模型<br/>Tab.1 Earthquake induced landslides density model under different slope range

表1 不同坡度下的地震滑坡密度模型
Tab.1 Earthquake induced landslides density model under different slope range

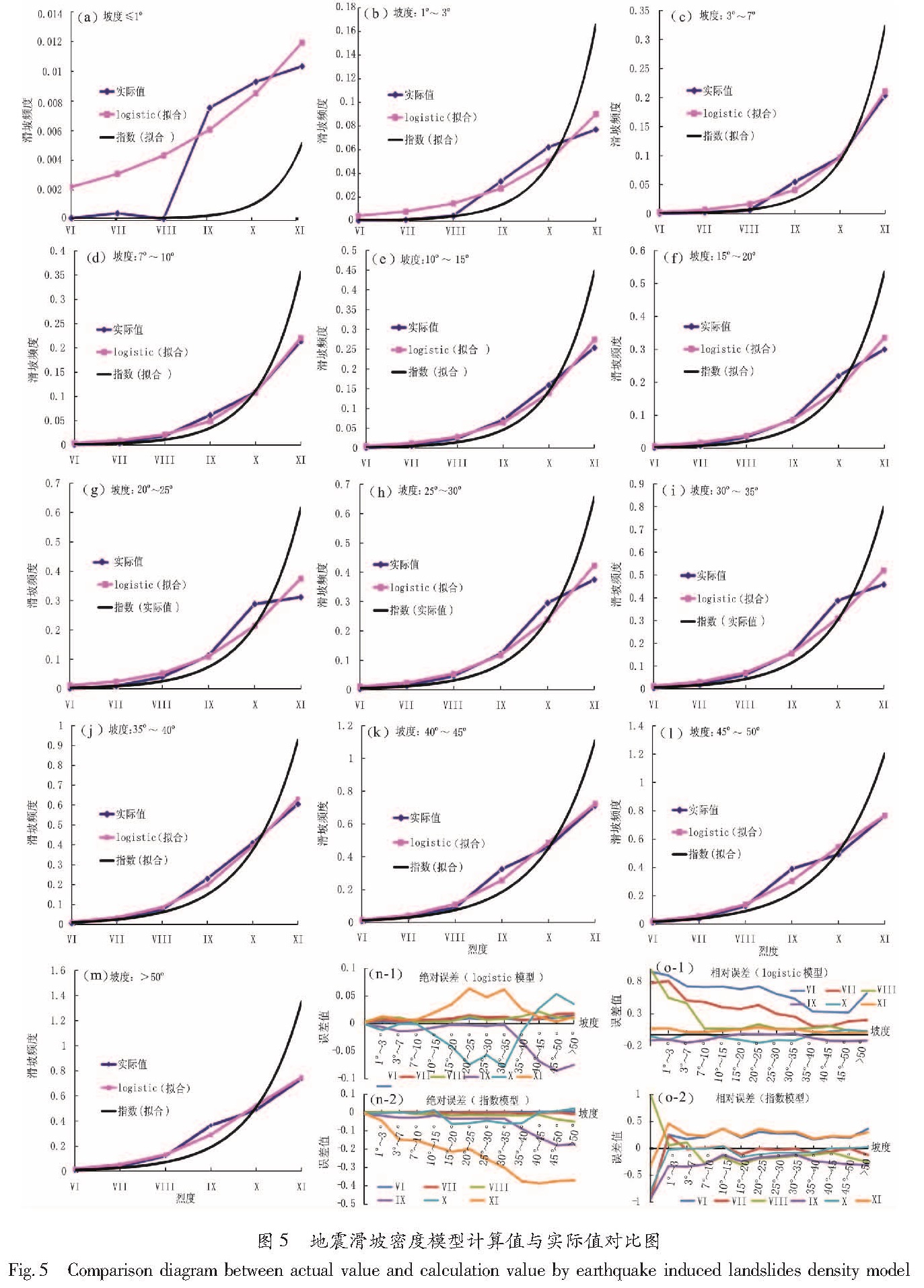
图5 地震滑坡密度模型计算值与实际值对比图<br/>Fig.5 Comparison diagram between actual value and calculation value by earthquake induced landslides density model

图5 地震滑坡密度模型计算值与实际值对比图
Fig.5 Comparison diagram between actual value and calculation value by earthquake induced landslides density model

图6 Ⅵ～Ⅺ 度下我国地震滑坡危险性预测<br/>Fig.6 Risk prediction of earthquake induced landslides in the intensity from Ⅵ to Ⅺ in China

图6 Ⅵ～Ⅺ 度下我国地震滑坡危险性预测
Fig.6 Risk prediction of earthquake induced landslides in the intensity from Ⅵ to Ⅺ in China

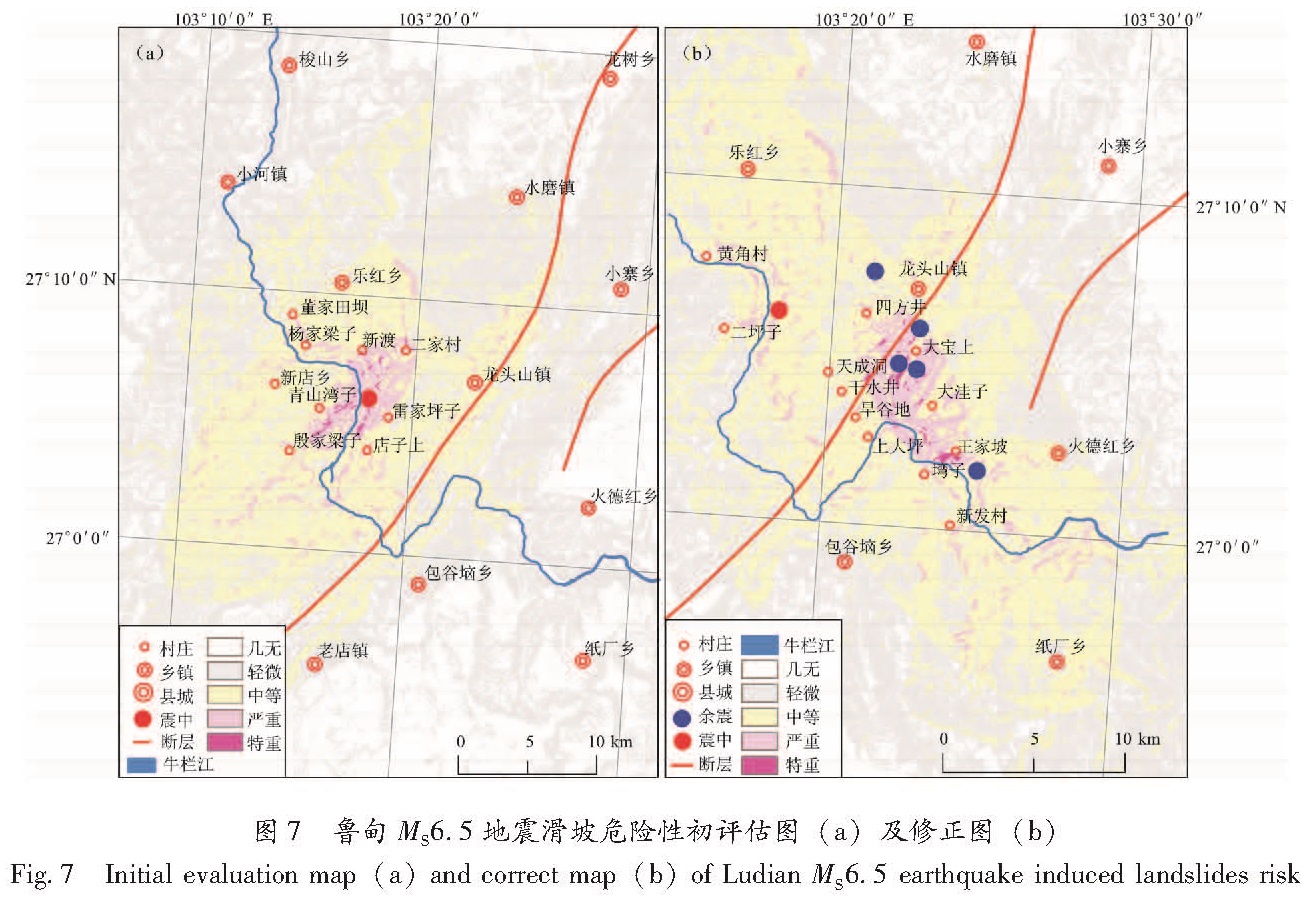
图7 鲁甸MS6.5地震滑坡危险性初评估图(a)及修正图(b)<br/>Fig.7 Initial evaluation map(a)and correct map(b)of Ludian MS6.5 earthquake induced landslides risk

图7 鲁甸MS6.5地震滑坡危险性初评估图(a)及修正图(b)
Fig.7 Initial evaluation map(a)and correct map(b)of Ludian MS6.5 earthquake induced landslides risk

白仙富,戴雨芡,戴靖,等.2013.昭通地区地震灾害区域性特征分析[J].地震研究,34(4):514-523.
白仙富,戴雨芡,赵恒.2014.地震影响场应急评估方法研究[J].自然灾害学报,23(4):91-102.
常隆庆.1938.四川叠溪地震调查记[J].地质评论,(3):251-292.
李世成,崔建文,乔森,等.2001.云南山地地震地质灾害对河流综合开发的影响[J].地震研究,24(2):140-145.
牛中齐,填海波,高武,等.2006.在山走动的地方[M].银川:宁夏人民出版社.
乔建平,蒲晓虹,王萌,等.2009.汶川地震滑坡的分布特点及最大震中距分析[J].自然灾害学报,18(5):10-15.
秦绪文,杨金中,张志,等.2008.汶川地震灾区航天遥感应急调查[M].北京:科学出版社.
孙崇绍,蔡红卫.1997.我国历史地震时滑坡崩塌的发育及分布特征[J].自然灾害学报,6(1):25-30.
唐川,黄楚兴,万晔.1997.云南省丽江大地震及其诱发的崩塌滑坡灾害特征[J].自然灾害学报,6(3):76-84.
唐川,朱静,张翔瑞.2001.GIS支持下的地震诱发滑坡危险区预测研究[J].地震研究,24(1):73-81.
陶舒,胡德勇,赵文吉,等.2010.基于信息量与逻辑回归模型的次生滑坡灾害敏感性评价[J].地理研究,29(9):1594-1605.
王秀英,聂高众,马牧军.2012.地震滑坡灾害评估中地震影响因素的联合应用[J].地震学报,34(1):76-84.
王秀英,聂高众,王松.2011.利用模糊数学方法建立汶川地震滑坡灾害评判标准[J].岩土力学,32(2):403-410.
谢毓寿,蔡美彪.1985.中国地震历史资料汇编(第四卷)[M].北京:科学出版社.
许冲,戴福初,肖建章.2011.“5·12”汶川地震诱发滑坡特征参数统计分析[J].自然灾害学报,20(4):147-153.
许冲,戴福初,姚鑫,等.2009.GIS支持下基于层次分析法的汶川地震区滑坡易发性评价[J].岩石力学与工程学报,28(z 2):3978-3985.
许冲,戴福初,姚鑫,等.2010.基于GIS的汶川地震滑坡灾害影响因子确定性系书分析[J].岩石力学与工程学报,29(1):2972-2980.
许冲,徐锡伟.2012.基于GIS与ANN模型的地震滑坡易发性区划[J].地质科技情报,31(3):116-121.
许国昌.1981.强震区人工岩质路堑边坡的破坏及稳定性分析[J].西北地震学报,(3):18-22.
游泽李,吴芝雄,谢乐今.1991.西藏察隅8.6级地震的烈度分布[J].东北地震研究,7(1):94-102.
袁一凡.2008.四川汶川8.0级地震损失评估[J].地震工程与工程振动,25(5):10-19.
朱海之,王克鲁,赵其强.1975.从昭通地震破坏看山区地震地面破坏特点[J].地质科学,(3):230-243.
庄建琦,崔鹏,葛永刚,等.2010.“5·12”汶川地震崩塌滑坡危险性评价[J].岩石力学与工程学报,29(z 2):3735-3742.
Koit,Hotta N.,Ishigaki I.,et al.2006.Prolonged impact of earthquake-induced landslides on sediment yield in a mountain watershed:the Tanzawa region,Japan[J].Geomorphology,81(1/2):166-184.
Marzoratis,Luzil.,De A.M..2002.Rock falls induced by earthquakes:a statistical approach[J].Soil Dynamics and Earthquake engineering,22(7):565-577.

备注

引言

1 数据和方法

2 地震滑坡影响因子分析

3 地震滑坡危险性模型

4 地震滑坡危险性评估模型初步应用

5 结论和讨论

期刊信息