(Institute of Geophysics,CEA,Beijing 100081,China)
Beijing Basin; basin amplification effect; high-rise building; risk level of seismic hazard
以北京盆地为例,针对不同的设定地震,研究了不同震源条件对盆地放大效应的影响。结果 表明:尽管震源因素可对计算结果带来一些不确定性,但盆地内沉积物的厚度是控制3～10 s周期段地震动加速度反应谱的主要因素。因此,计算了盆地对3～10 s周期段地震动加速度反应谱的平均放大系数,并通过回归分析得到了平均放大系数与盆地等效沉积物厚度之间的函数关系。最后,结合北京盆地内高层建筑的分布,初步探讨了高层建筑地震致灾风险水平与盆地结构的关系。
Taking Beijing Basin as an example,we set up several scenario earthquakes,and study the influence of the different epicenter condition on the basin amplification effect of ground motion.The research result demonstrates that although the different source factor may cause the uncertainty to the calculation result in a certain extent,the basin amplification effect on 3～10 s ground motion acceleration response spectrum is mainly controlled by the thickness of sediment in basin.Thus,the average basin amplification factor on 3～10 s ground motion acceleration response spectrum is computed,and the correlation function which is between the average amplification factor and equivalent thickness of sediment in basin is analyzed.Finally,according to the distribution of high-rise buildings in Beijing Basin,we preliminarily discuss the relationship between risk level of seismic hazard of high-rise buildings and basin structure.
盆地作为一类特殊的场地,对地震动有选择性放大作用,其原因主要归结为两个方面:一是盆地内相对松软的物质组成与外部基岩之间具有较强的波阻抗差异,通常波阻抗差异越明显,盆地对地震动的放大效应越大; 二是盆地的几何结构会导致复杂的地震波成分产生,如盆地边缘激发出地震面波而形成“边缘放大效应”,以及盆地结构的聚焦效应等(Field,the SCEC Phase III Working Group,2000; Graves,1993; Kawase,1996)。相关研究表明:盆地对高频地震动成分的放大作用较为复杂,但是对1 s以上长周期地震动的放大作用与盆地内沉积物的厚度之间具有显著的正相关性,如Bindi 等(2009)、Campbell(1997)、Day等(2005)、Field(2000)、Fletcher和Wen(2005)、Alejandro等(2002)、Hruby和Beresnev(2003)、Lee等(2008)、Olsen(2000)、Rogers等(1985)、高孟潭等(2002)以及潘波等(2006,2009)在研究洛杉矶、台北、Gubbio和北京等不同盆地对地震动的放大作用后,得到了类似的结论。在上述学者关于盆地放大效应的研究结果中,有单独针对某次具体地震下的计算结果,也有某几次地震作用下的平均计算结果,但多数没有给出用于定量计算盆地放大因子的数学公式。Day等(2005)和Field(2000)曾分别将1.5 km/s和2.5 km/s剪切波速度界面的埋深作为盆地深度,拟合出了盆地放大因子与盆地深度之间的函数关系。然而付长华等(2012)认为,当盆地中包含多层不同的沉积介质时,这种盆地深度的定义方式可能过于简单,因而提出了“盆地等效沉积物厚度”的概念。
在历史上的几次大地震中,由于盆地对长周期地震动的选择性放大作用,盆地内高层建筑与长周期地震动共振往往受损更为严重(郝敏等,2005; 廖仲远,1997; 孙振凯,张洪由,2001; 吴济民,1987; 竹内敬二,赵仕万,1986)。北京坐落于盆地中,近年来,20层以上的高层建筑快速发展。此类高层建筑的自振周期通常为3 s以上,因而有可能与3 s以上长周期地震动发生共振而产生地震灾害。目前,关于北京盆地对地震动的放大效应的研究已开展了一些工作,但这些研究结果有些是定性的,有些是针对峰值地面运动速度(PGV)和傅立叶谱的,不能直接为工程结构的抗震设防提供依据。所以,本文以北京盆地为例,采用有限差分地震动数值模拟方法来研究盆地对3～10 s地震动加速度反应谱的放大作用。尝试构建出用于定量计算盆地放大作用的函数关系,为北京的城市未来规划、高层建筑的震害防御、地震应急准备以及地震救援工作提供科学的参考。
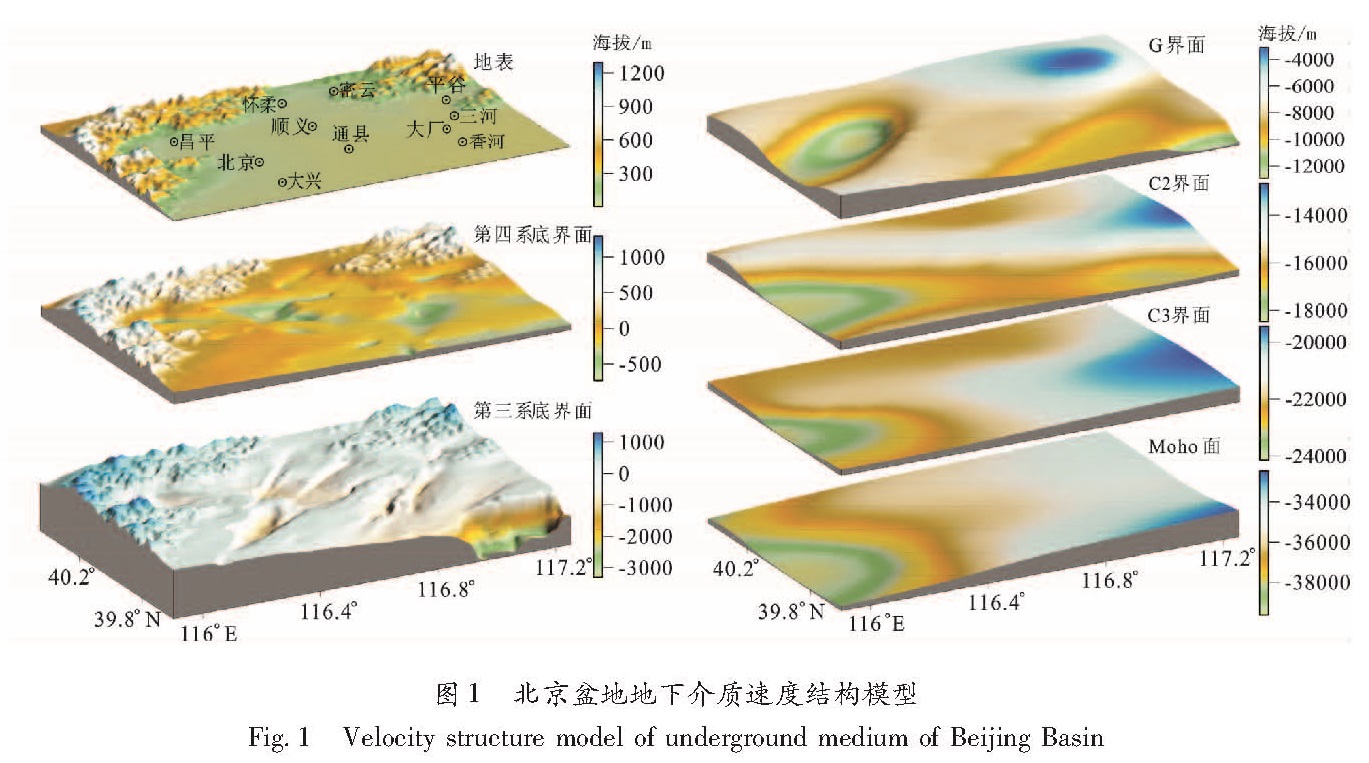
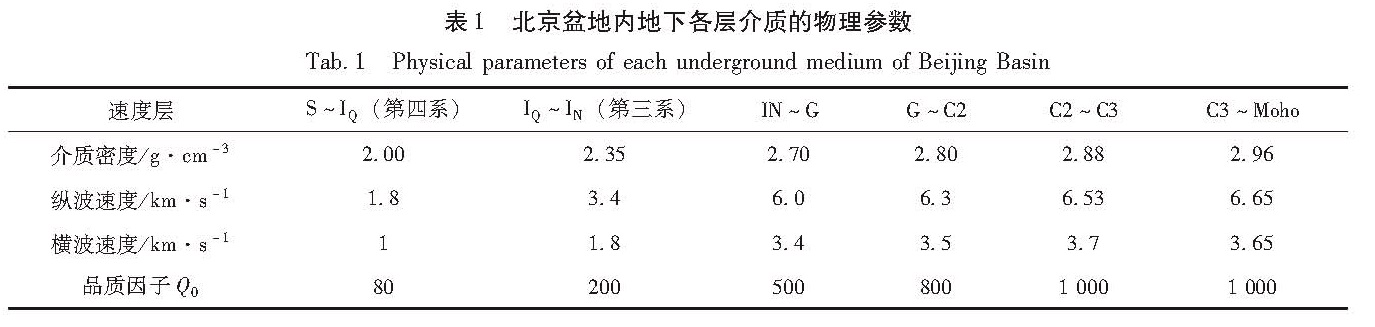
本文采用并行化有限差分数值算法(张伟,2006)模拟北京盆地内的地震动传播过程。模拟地震动的前提是建立目标区地下介质速度结构模型,并设定合理的震源参数。北京盆地地下介质速度结构模型使用付长华等(2012)建立的模型,如图1所示。该模型包含6层不同的介质,由7个层界面分隔开来。自地表往下,7个层界面依次为地表(S)、第四系底界面(IQ)、第三系底界面(IN)、G界面、C2界面、C3界面和Moho面,各个层界面的海拔数据可见其右方图例。6层不同介质的波速、密度以及介质品质因子等计算参数列于表1。
图1 北京盆地地下介质速度结构模型
Fig.1 Velocity structure model of underground medium of Beijing Basin
表1 北京盆地内地下各层介质的物理参数
Tab.1 Physical parameters of each underground medium of Beijing Basin
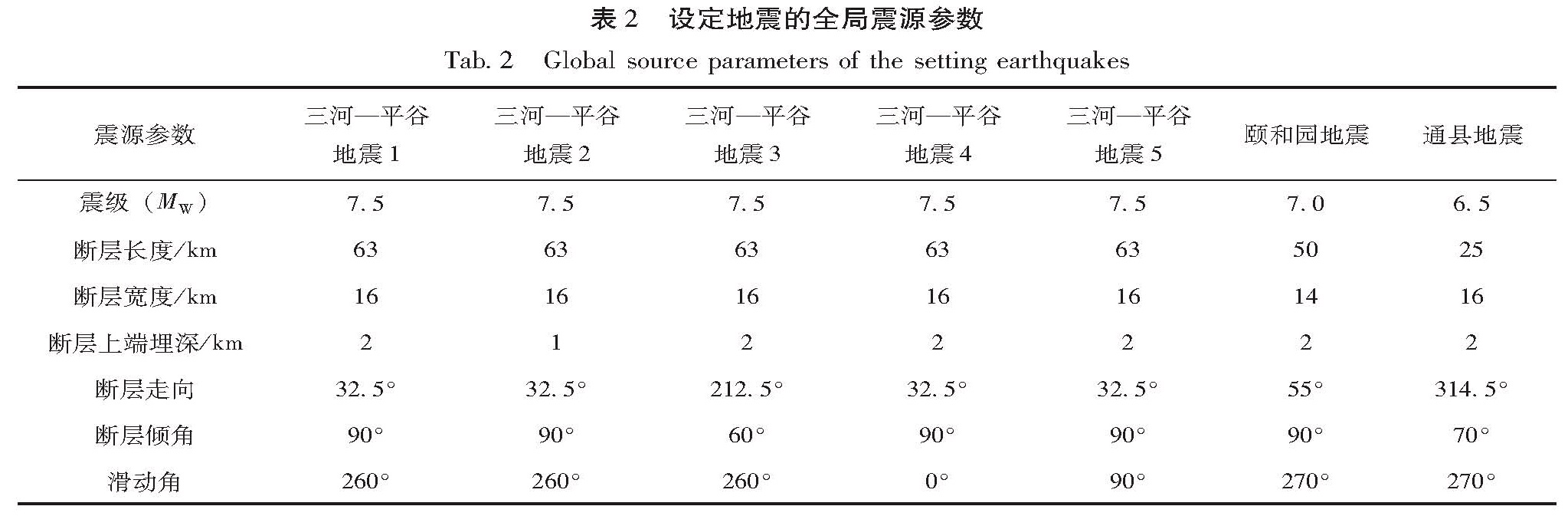
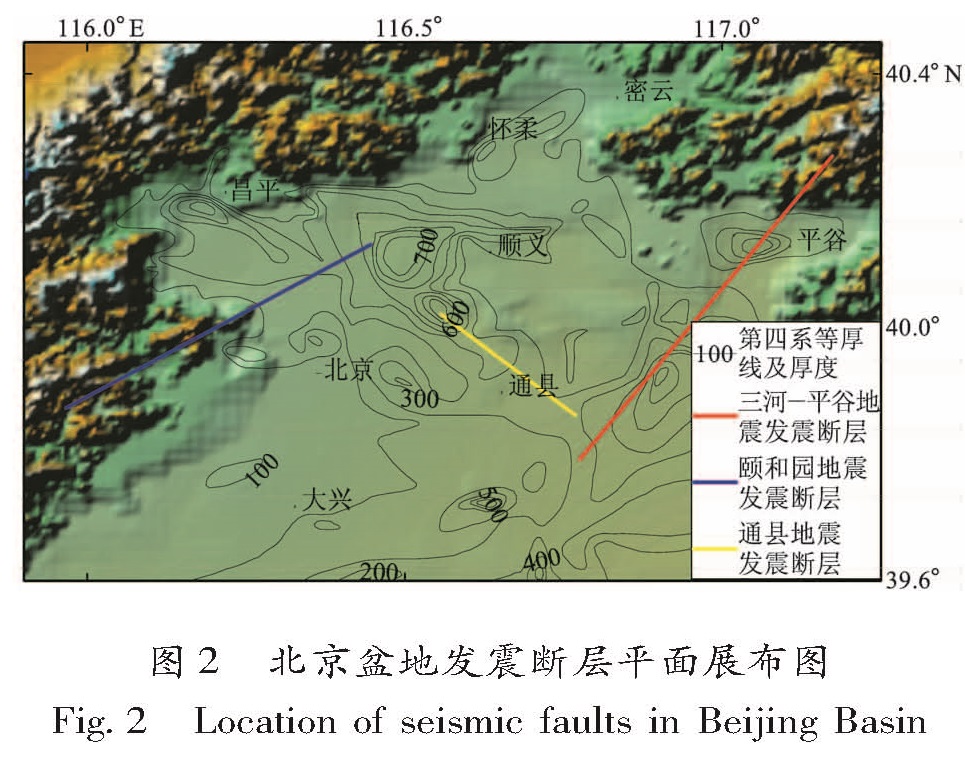
为了研究不同震源条件对计算结果的影响,本文共使用了7个设定地震,各个设定地震的全局震源参数见表2,其中三河—平谷地震1和颐和园地震的震源参数参考了相应历史地震的考察资料(高孟潭等,2002); 三河—平谷地震2～5是对三河—平谷地震1的震源参数稍做修改而定的,目的是为了研究当断层倾角、断层上断点埋深和滑动角中的任一因素发生改变时,会引起盆地对地震动产生哪些不同的放大效应; 通县地震则是根据此处活动断层的特征而设定,其震级与发震断层的长宽满足前人的研究成果(沈建文等,1990)。设定地震的发震断层的平面位置如图2所示,其中三河—平谷地震1～5的发震断层的平面位置重合。
表2 设定地震的全局震源参数
Tab.2 Global source parameters of the setting earthquakes
设定地震的断层面上的凹凸体的设定遵循Somerville等(1999)的规则,设定地震的凹凸体分布、初始破裂点以及破裂方式等局部震源参数
图2 北京盆地发震断层平面展布图
Fig.2 Location of seismic faults in Beijing Basin
如图3所示。其中三河—平谷地震1～5的凹凸体分布、初始破裂点以及破裂方式一致。图3中黄色区域为凹凸体的分布位置,红色六角星形代表初始破裂点,圆形虚线表示破裂以初始破裂点为中心、并以相等的速度向四周传播。根据地震观测资料和反演结果,断层面的平均破裂传播速度一般为剪切波速度的0.7～0.9倍,约2.5～3.0 km·s-1,本文在计算时取为2.8 km·s-1。
盆地内强地面运动特性与震源特性、震源—盆地位置关系(地震波传播路径)、盆地几何结构以及盆地内填沉积物属性等密切相关。通过对比盆地内外地震动强度、频谱特征、持时以及衰减
图3 断层面上凹凸体分布、初始破裂点位置及破裂方式(a)三河—平谷地震1～5;(b)颐和园地震;(c)通县地震
Fig.3 Distribution of asperity,the location of the initial rupture point and the rupture pattern on fault plane(a)Sanhe-Pinggu earthquake 1～5;(b)Yiheyuan earthquake;(c)Tongxian earthquake
特征之间的差异可以发现:盆地作为一类特殊的地质构造,对地震动有着显著的放大效应(Field,2000; Hruby,Beresnev,2003)。图4列举了在三河—平谷地震1作用下、3 s周期时北京盆地内地表地震动加速度反应谱值的分布情况,从图中可以较清楚看到盆地内沉积物厚度大的区域,如顺义、昌平等凹陷处,比其周围区域具有更大的反应谱值,这体现了盆地结构对地震动的放大效应。
图4 3 s周期时地表地震动加速度反应谱
Fig.4 Acceleration response spectrum of ground motion at period of 3 s
以理想平层模型作为参考场地的方法可以消除震源特性对盆地内地震动的影响,从而凸现盆地结构对地震动的放大作用。然而,震源相对于盆地的不同位置关系仍会使得地震波进入盆地的方向不同,进而可能在某些位置处激发不同的盆地响应结果。因此所求得的盆地放大系数中,仍包含了震源因素导致的某些不确定性成分(Olsen,2000; Choi et al.,2005)。
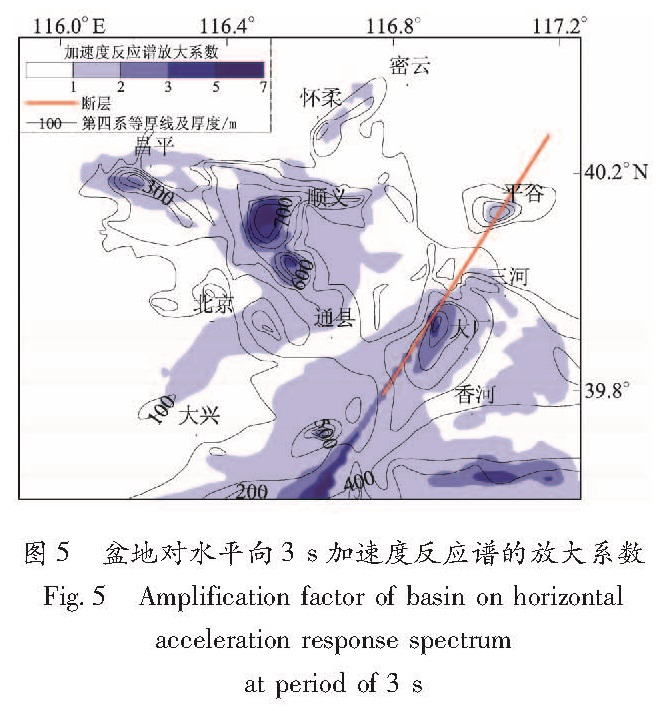
本文计算了北京盆地对地表加速度反应谱的放大系数(即基于盆地模型计算得到的地表加速度反应谱值与基于平层模型的加速度反应谱值之比,下文简称“盆地放大系数”)。图5为盆地对水平向3 s加速度反应谱的放大系数。图中显示:(1)盆地放大系数大小与第四系厚度大小基本对应,第四系厚度大的区域,盆地放大系数相应也大,如顺义、大厂、昌平等次级凹陷处。特别是顺义凹陷的中心部位,第四系厚度超过700 m,盆地放大系数高达7倍;(2)第三系厚度大的区域(结合图4中标注的第三系等深线来看),盆地放大系数也较大。如香河以南的次级凹陷,第三系沉积厚约2 000 m,盆地放大系数可达5倍,北京市区第三系厚度超过1 000 m,盆地放大系数约为2倍左右。由此可见盆地内沉积物的厚度,包括第四系厚度和第三系厚度,都是影响盆地放大效应的主要因素,这与有关研究结果是一致的(Alejandro et al.,2002; Fletcher,Wen,2005; Hruby,Beresnev,2003; Lee et al.,2008; Rogers et al.,1985; Olsen,2000); 此外,结合图4与图5可以看出:顺义凹陷处第四系最厚超过700 m,第三系厚度约200 m,盆地放大系数为7倍; 香河以南凹
图5 盆地对水平向3 s加速度反应谱的放大系数
Fig.5 Amplification factor of basin on horizontal acceleration response spectrum at period of 3 s
为了反映不同地震作用下盆地放大系数的差异程度,本文以三河—平谷地震1作用下的盆地放大系数作为参考,计算了其它地震作用下地表各点的盆地放大系数与前者之差,并将这种差值按大小划分成若干区间。如果将地表每个点视为一个样本,则根据各区间内的样本数量可以大致体现震源因素变化对盆地放大系数产生的影响。
设参考地震和与之相比的另一次地震作用下地表某点的盆地放大系数分别为β1和β2,则两者之差的绝对值为Δβ=|β1-β2|,根据该点Δβ值的大小可以确定该点归属于何类区间。同时考虑到某些点虽然在两次地震作用下的盆地放大系数的绝对差值较大,但其相对变化率却比较小(例如两次地震作用下的盆地放大系数分别为10和12,绝对差值为2,但相对变化率仅为20%),于是我们再以相对变化率(即差异百分比:E=Δβ/β1×100%)对原来的分区加以约束,以保证这些相对变化率较小的点不至于归属到盆地放大系数异常变化的区间内。因此,最终的分区标准是综合考虑和值而确定,各差异区间的参考阈值如下:(1)Ⅰ类区间:Δβ≤0.25或E≤5%;(2)Ⅱ类区间:0.25≤Δβ≤0.5或5%≤E≤10%;(3)Ⅲ类区间:0.5≤Δβ≤1或10%≤E≤20%;(4)Ⅳ类区间:1≤Δβ≤2或20%≤E≤50%;(5)Ⅴ类区间:Δβ>2且E≥50%。
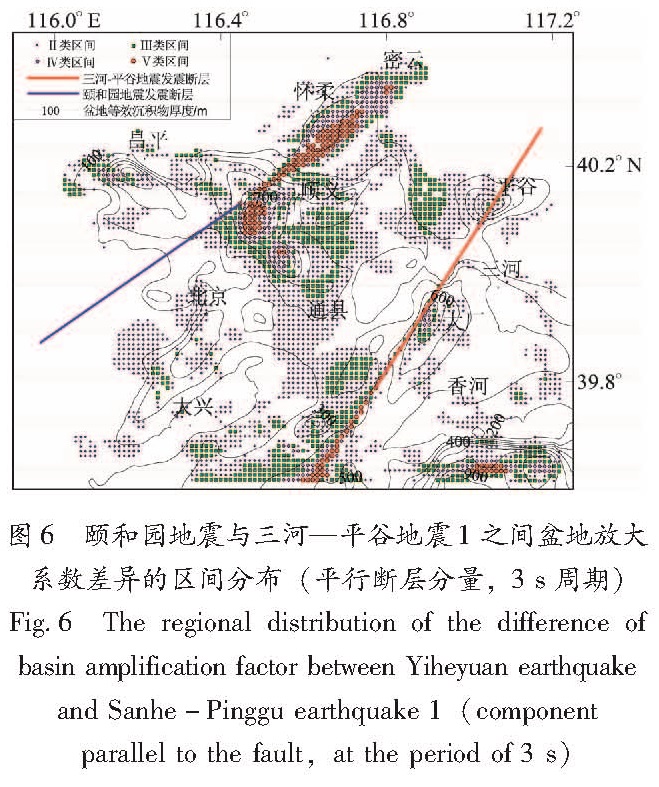
这两次地震作用导致的盆地放大系数差异见表3。这种差异的主要特点可归结为:(1)平行断层分量上的盆地放大系数受震源因素影响最大,垂直断层分量次之,竖向分量最小;(2)对于每个分量,3 s周期时盆地放大系数间的差异最大,基本上有20%～30%左右的样本位于Ⅱ类区间,但随着周期的增大,差异程度迅速减小,到5 s周期时绝大多数样本均位于Ⅰ类区间;(3)差异较大的地区主要包括:三河—平谷断层分布位置处、第四系和第三系沉积厚度大的地方,如顺义、怀柔和香河以南凹陷内,如图6所示(为了便于观察,位于I类区间的样本点未标注于图中)。其中,顺义和怀柔处差异较大,还有可能是位于颐和园发震断层前端的原因,因为断层破裂的方向性效应可能导致地震波在盆地特殊构造区域发生复杂的变化。
图6 颐和园地震与三河—平谷地震1之间盆地放大系数差异的区间分布(平行断层分量,3 s周期)
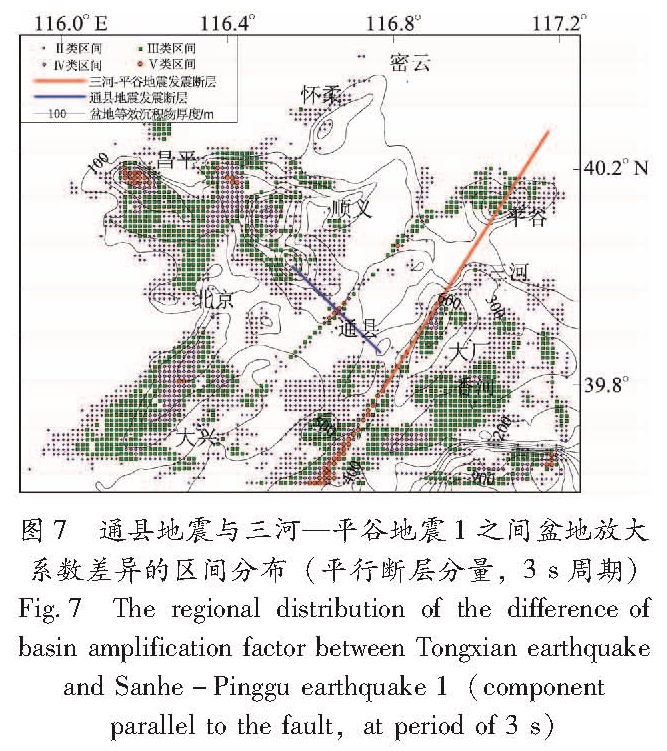
Fig.6 The regional distribution of the difference of basin amplification factor between Yiheyuan earthquake and Sanhe-Pinggu earthquake 1(component parallel to the fault,at the period of 3 s)
表3 颐和园地震与三河—平谷地震1作用下,不同分量和不同周期时地表各点盆地放大系数差异在各区间内的样本数百分比(%)
Tab.3 Percentage of specimen in each interval where the difference of basin amplification factors of different components located in different periods under Yiheyuan earthquake and Sanhe-Pinggu earthquake 1(%)
这两次地震作用导致的盆地放大系数差异见表4。差异的分布特征与由表3中的基本相似,差异较大之处位于图7中的三河—平谷断层周围、第四系和第三系厚度大的区域,如昌平、顺义、北京和大厂凹陷内。
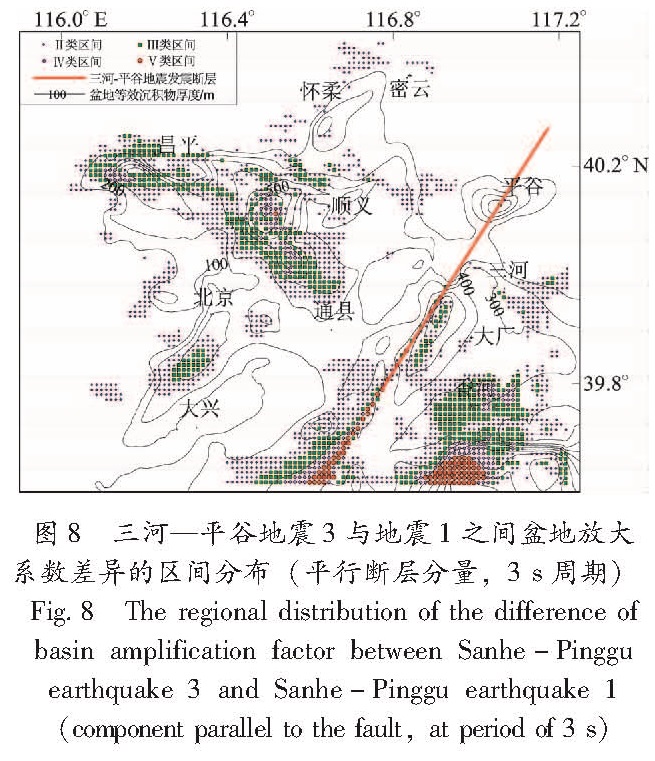
两次设定地震的其它震源参数全部一致,只考虑断层倾角分别为60°和90°时,盆地放大系数的差异。从表5可以看出,除平行断层分量上3 s周期时盆地放大系数之间的差异较大外,其它情况下样本基本位于Ⅰ类区间。差异较大的地区主
表4 通县地震与三河—平谷地震1作用下、不同分量和不同周期时地表各点盆地放大系数差异在各区间内的样本数百分比(%)
Tab.4 Percentage of specimen in each interval where the difference of basin amplification factors of different components located in different periods under Tongxian earthquake and Sanhe-Pinggu earthquake 1(%)
表5 三河—平谷地震3与地震1作用下、不同分量和不同周期时地表各点盆地放大系数差异在各区间内的样本数百分比(%)
Tab.5 Percentage of specimen in each interval where the difference of basin amplification factors of different components located in different periods under Sanhe-Pinggu earthquake 3 and Sanhe-Pinggu earthquake 1
图7 通县地震与三河—平谷地震1之间盆地放大系数差异的区间分布(平行断层分量,3 s周期)
Fig.7 The regional distribution of the difference of basin amplification factor between Tongxian earthquake and Sanhe-Pinggu earthquake 1(component parallel to the fault,at period of 3 s)
图8 三河—平谷地震3与地震1之间盆地放大系数差异的区间分布(平行断层分量,3 s周期)
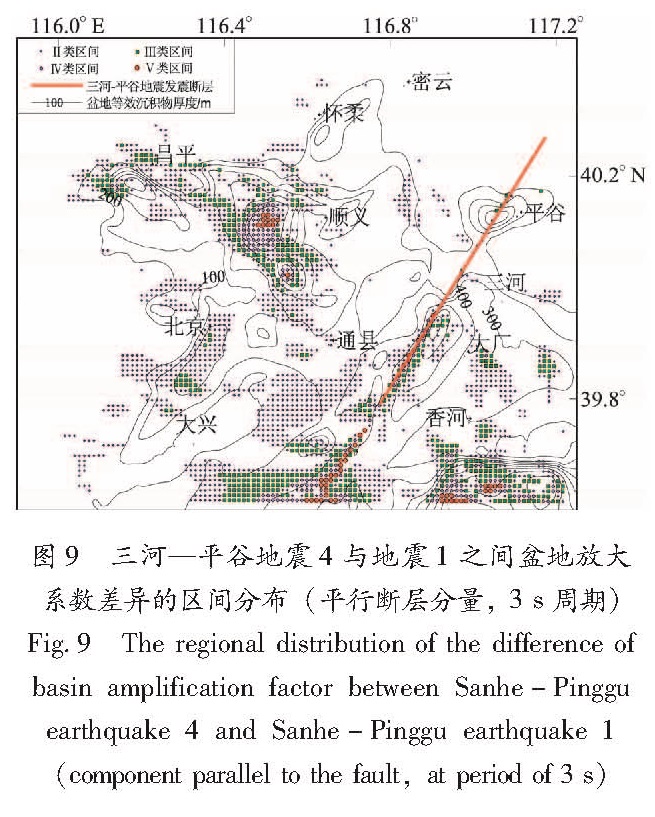
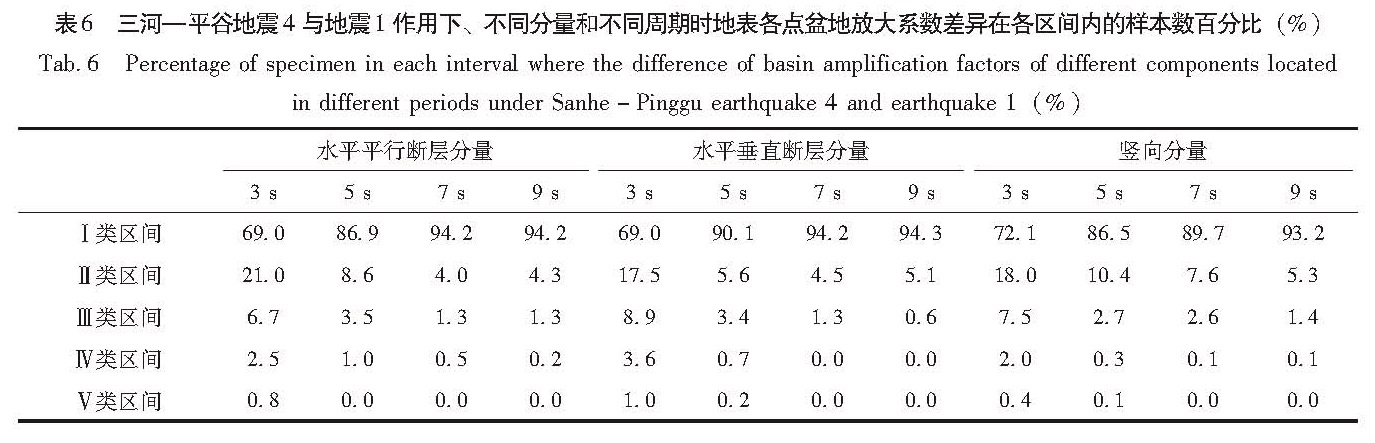
Fig.8 The regional distribution of the difference of basin amplification factor between Sanhe-Pinggu earthquake 3 and Sanhe-Pinggu earthquake 1(component parallel to the fault,at period of 3 s)
两次设定地震的其它震源参数全部一致,只考虑滑动角分别为0°和260°时,即走滑机制和正断层机制两种情况下盆地放大系数的差异。从表6可以看出,3 s周期时盆地放大系数之间的差异较大,其中平行断层分量上的差异程度最高,但到5 s周期时差异已很小。图9同样显示了差异较大的地区是断层的分布位置处以及第四系和第三系厚度大的区域。
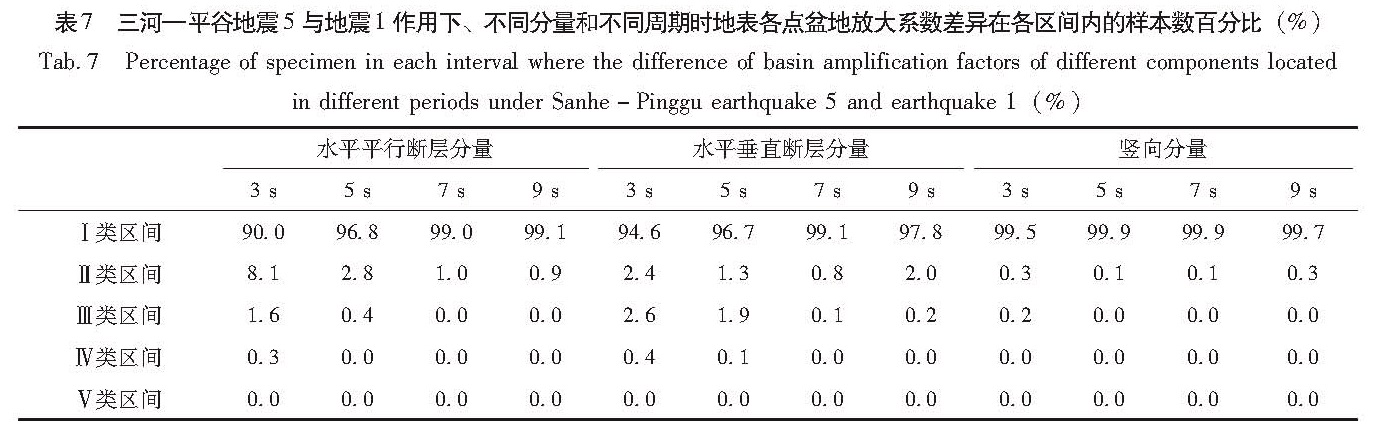
两次设定地震的其它震源参数全部一致,只考虑滑动角分别为90°和260°时,即逆冲机制和正断层机制两种情况下盆地放大系数的差异。从表7可以看出,3 s、5 s、7 s和9 s 4个周期时盆地放大系数之间的差异不大,有90%以上的样本位于Ⅰ类区间,可以认为正断层与逆断层两种情况下的盆地放大系数基本一致。这可能是由于两种情况下的地震矩以应力形式施加到同一子源网格点时,只是方向相反但大小基本保持不变的原因。
图9 三河—平谷地震4与地震1之间盆地放大系数差异的区间分布(平行断层分量,3 s周期)
Fig.9 The regional distribution of the difference of basin amplification factor between Sanhe-Pinggu earthquake 4 and Sanhe-Pinggu earthquake 1(component parallel to the fault,at period of 3 s)
表6 三河—平谷地震4与地震1作用下、不同分量和不同周期时地表各点盆地放大系数差异在各区间内的样本数百分比(%)
Tab.6 Percentage of specimen in each interval where the difference of basin amplification factors of different components located in different periods under Sanhe-Pinggu earthquake 4 and earthquake 1(%)
表7 三河—平谷地震5与地震1作用下、不同分量和不同周期时地表各点盆地放大系数差异在各区间内的样本数百分比(%)
Tab.7 Percentage of specimen in each interval where the difference of basin amplification factors of different components located in different periods under Sanhe-Pinggu earthquake 5 and earthquake 1(%)
两次设定地震的其它震源参数全部一致,只考虑断层上断点埋深分别为1 km和2 km时盆地放大系数的差异。从表8可以看出,在3 s、5 s、7 s和9 s 4个周期时,几乎所有样本均位于Ⅰ类区间,可以认为断层上断点埋深的变化对盆地放大系数没有影响。
表8 三河—平谷地震2与地震1作用下、不同分量和不同周期时地表各点盆地放大系数差异在各区间内的样本数百分比(%)
Tab.8 Percentage of specimen in each interval where the difference of basin amplification factors of different components located in different periods under Sanhe-Pinggu earthquake 2 and earthquake 1(%)
综上所述,可以得到以下结论:
(1)震源因素会导致盆地放大效应的不确定性,尤其是对3 s周期水平向平行断层分量上的盆地放大系数影响最大。差异较大之处主要位于断层展布处、断层破裂的前端、第四系和第三系厚度大的地方。
(2)地震波进入盆地的位置不同,会导致不同的盆地响应。因此,发震断层几何位置的改变对盆地放大系数的影响最大; 其次,当发震断层在水平面内的位置不变时,走滑断层机制与倾滑断层机制会产生不同的盆地放大特征,断层倾角的变化对盆地放大效应也有影响; 然而,对于同一断层面,震源为逆冲机制和正断层机制两种情况下盆地放大系数的差异很小,上断点埋深的变化对盆地放大效应的影响也基本可以忽略。
(3)虽然震源因素会在一定程度上造成盆地放大效应的差异,但盆地内沉积物的厚度是影响盆地对3～10 s地震动加速度反应谱放大的主导因素。盆地对加速度反应谱的放大系数与盆地内沉积物的厚度之间关系密切,近地表的第四系和第三系的厚度都对盆地放大效应有很大的影响,其中第四系的影响程度更为突出。
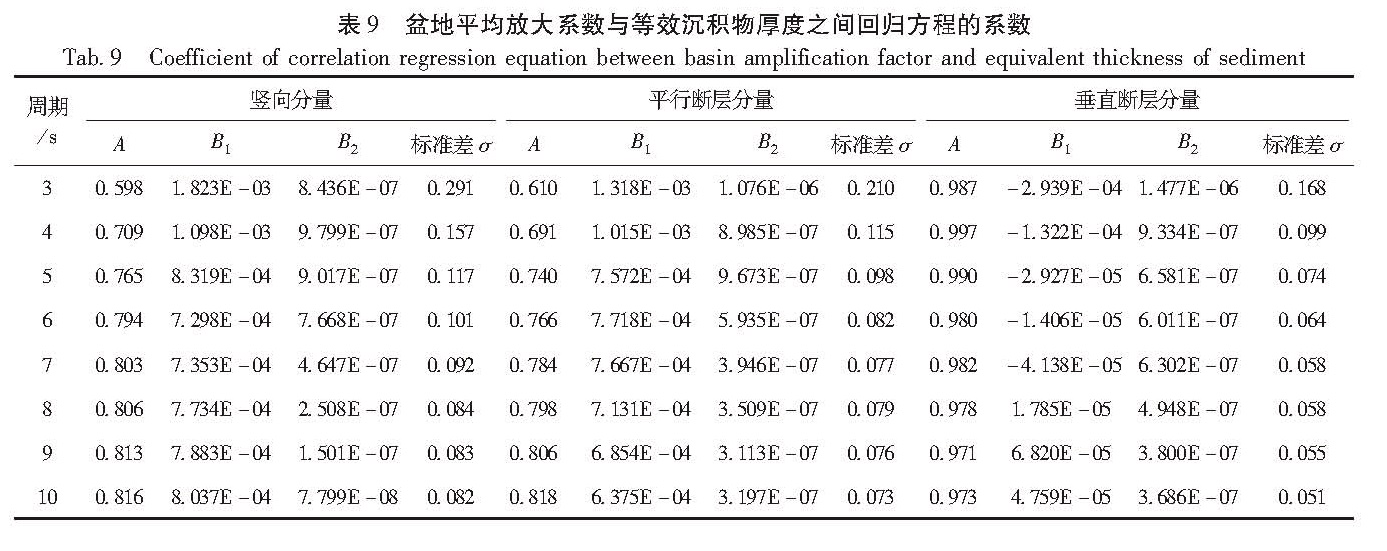
上述研究表明:盆地内沉积物(包括第四系和第三系)的厚度是影响盆地放大效应的主要因素。因此,我们可以对多次设定地震下的盆地放大系数取平均,以求解盆地对加速度反应谱的平均放大行为,继而可以构建出盆地平均放大系数与盆地内沉积物厚度的函数关系。由于三河—平谷地震2和地震1的盆地放大系数几乎没有差异,所以在求取盆地平均放大系数时没有包含此次地震的计算结果。至于震源因素对盆地放大系数带来的不确定性,则可以考虑在回归函数的基础上加上几倍标准差的形式来包容。鉴于盆地内第四系和第三系的厚度均对盆地放大系数有较大的影响,我们引入了“等效沉积物厚度”的概念,其定义为把第三系等效为第四系后的厚度与真实第四系的厚度相加得到的厚度值(付长华等,2012)。
H=(ρQ·Vs2Q)/(ρN·Vs2N)×HN+HQ.(1)
式中,H即等效沉积物厚度; ρQ、VsQ、HQ分别是第四系的密度、横波速度和厚度; ρN、VsN、HN分别是第三系的密度、横波速度和厚度。
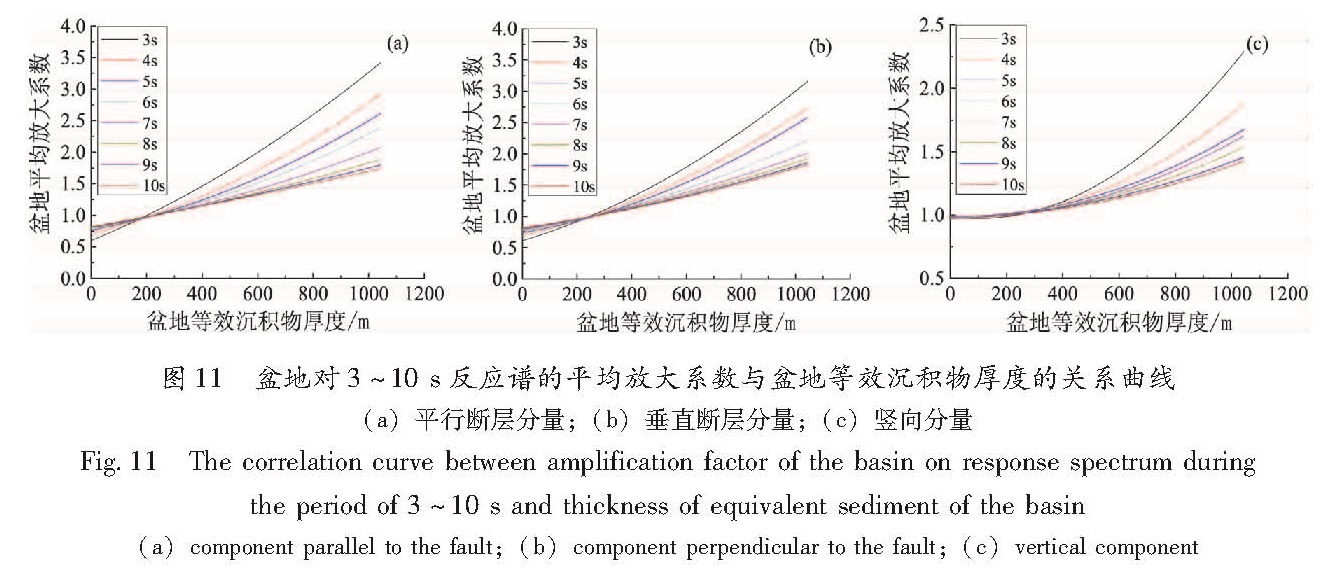
图 10为3个分量上盆地放大系数与等效沉积物厚度之间相关性函数的拟合结果。从图中可以看出:(1)对于两个水平分量,3 s周期时样本的离散性都比较大,但随着周期的增大,离散性均迅速减小; 此外,平行断层分量上盆地放大系数随等效沉积物厚度的变化率略大于垂直断层分量;(2)与水平分量相比,竖向分量上盆地结构对加速度反应谱的平均放大系数随等效沉积物厚度的变化率要小得多;(3)三分量的拟合结果都表明,随着周期增大,盆地结构对加速度反应谱的平均放大系数随等效沉积物厚度的变化率减小。这意味着在3～10 s周期段,盆地结构对3 s周期地震动加速度反应谱的放大作用最为显著,随反应谱周期增大,放大作用逐渐减弱。
若设盆地放大系数与等效沉积物厚度之间的相关性曲线表现为
β=A+B1×H+B2×H2.(2)
利用最小二乘法对盆地内所有样本点数据进行拟合,我们建立了盆地结构对3～10 s加速度反应谱的平均放大系数与等效沉积物厚度之间的相关性方程,回归系数A、B1和B2的值列于表9中。式(2)中,β是盆地结构对加速度反应谱的平均放大系数,H是等效沉积物厚度(单位:m)。
图 10 盆地放大系数与等效沉积物厚度的关系
(a)平行断层分量;(b)垂直断层分量;(c)竖向分量
Fig.10 Relationship between basin amplification factor and thickness of equivalent sediment(a)component parallel to the fault;(b)component perpendicular to the fault;(c)vertical component
表9 盆地平均放大系数与等效沉积物厚度之间回归方程的系数
Tab.9 Coefficient of correlation regression equation between basin amplification factor and equivalent thickness of sediment
根据表9中的回归系数,本文分别得到了3个分量上盆地对3～10 s加速度反应谱的平均放大系数与盆地等效沉积物厚度的关系曲线,如图 11所示。从图中可以看出:3个分量的盆地放大系数均随盆地等效沉积物厚度的增加而增大,随反应谱周期的增大而减小; 对于两水平分量,当等效沉积物厚度小于200 m时,盆地放大系数小于1。造成这种现象的主要原因在于当初构建的理想平层模型中包含了约200 m厚的沉积物(这个厚度是对盆地模型沉积物厚度加权平均后的结果)。因为实际记录到的地震动往往经历了平均场地的放大作用(Day et al.,2005),建立这样的参考平层模型近似于把计算结果增加了一次平均场地的校正。在实际应用中,可人为地将该段放大系数取值为1。
图 12对3个分量的盆地平均放大系数进行了对比。可以看出:盆地结构对不同周期加速度反应谱的平均放大系数以及各自加1倍标准差(+σ)的结果,水平平行断层分量总是大于垂直断层分量。因此,本文将平行断层分量的回归结果作为确定水平向盆地放大效应的依据。盆地对竖向分量的放大作用在等效沉积物厚度大于200 m时较水平分量小,但在等效沉积物厚度小于200 m时较水平分量大。
图 11 盆地对3～10 s反应谱的平均放大系数与盆地等效沉积物厚度的关系曲线(a)平行断层分量;(b)垂直断层分量;(c)竖向分量
Fig.11 The correlation curve between amplification factor of the basin on response spectrum during the period of 3～10 s and thickness of equivalent sediment of the basin
图 12 3个分量上的盆地平均放大系数对比(a)3 s;(b)5 s;(c)7 s
Fig.12 Comparison of average basin amplification factor of three components
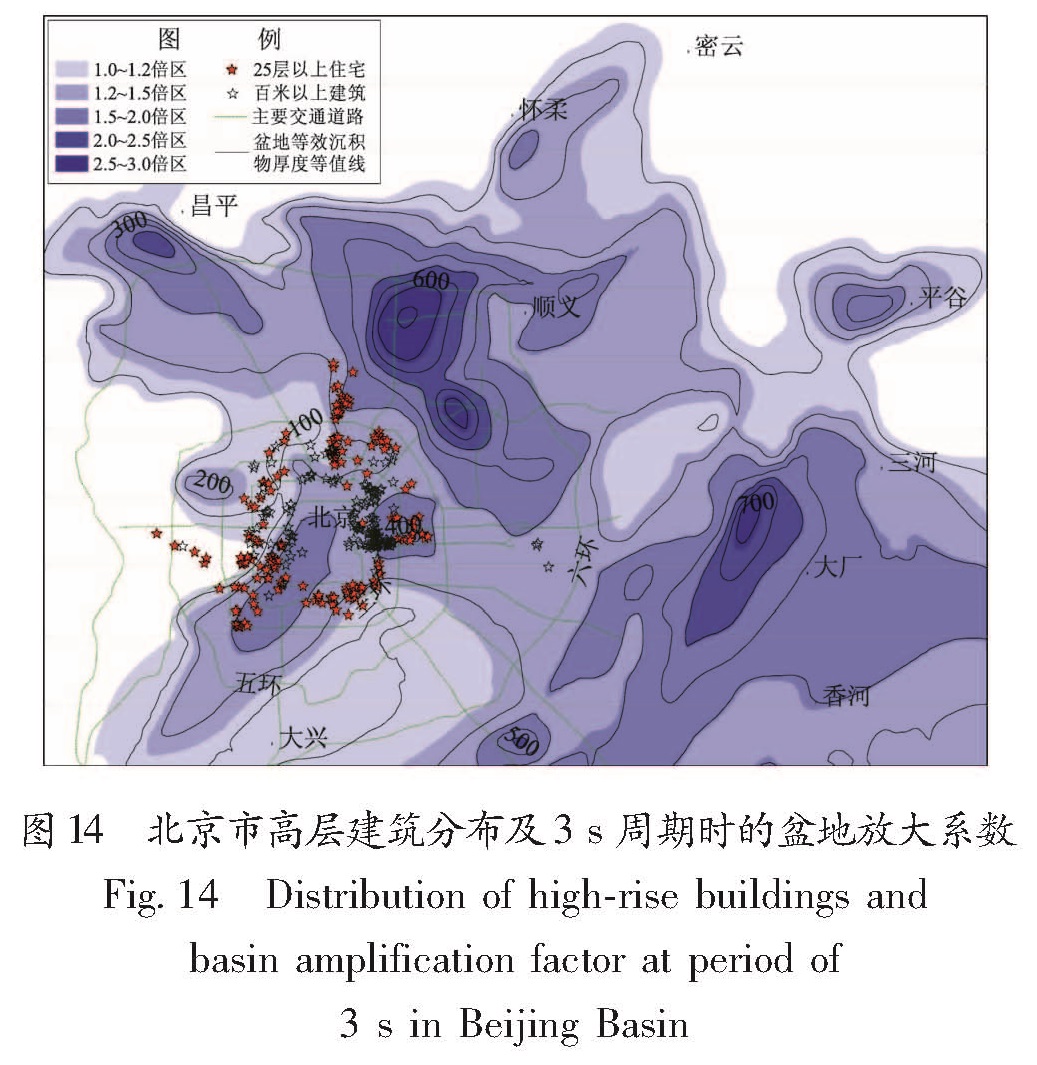
由于文中盆地放大系数的有效周期范围在3 s以上,所以,我们只对自振周期大约在3 s以上的高层建筑进行了统计。这些建筑包括百米以上超高层商务楼以及25层以上住宅楼,它们在盆地中的分布位置见图 14,主要集中在4个区域:(1)中央商务区(CBD)及以东地区。其中,CBD是指东二环到东四环之间的中央商务区,以东三环中路为南北主轴线,该区集中了北京绝大部分超高层商务楼;(2)西二环到西三环之间,超高层商务楼和住宅楼均有分布;(4)北四环东路以北地区,主要为居民住宅楼;(4)南三环东路为中心的区域,也基本上为住宅楼的形式。
对于一般钢筋混凝土结构,自振周期T与建筑层数N足关系式由脉动实测数据统计而来,可表示为T=k*N,k是影响系数,其范围是0.05～0.1(GB50009—2001)。本文在计算时,k取中间值0.075。然而地震时,建筑结构自振周期会有所增加,由脉动法给出的结果尚应乘以某一增大系数,以对应于地震时结构的自振周期值(包世华,方鄂华,1989)。根据王广军和樊水荣(1989a,b)的研究结论,文中增大系数取为1.5。
图 13展示了北京盆地内高层建筑自振周期与建筑栋数的对应情况,可以直观地看到统计范围内的绝大多数高层建筑的自振周期介于2.6～3.6 s。结合表 10可以更清楚地知道此类高层建筑的层数都在32层以内。其次,33～40层之间的建筑约占统计样本总量的8.8%,自振周期范围为3.7～4.5 s。40层以内的高层建筑在北京市的四面均有分布。超过40层的建筑主要以商务楼的形式分布于CBD,其中最高为80层,自振周期长达9.0 s。
图 13 北京盆地内高层建筑自振周期与建筑栋数统计
Fig.13 Statistics of self-vibrating periods and the amount of high-rise buildings in Beijing Basin
表 10 北京盆地内高层建筑的高度及自振周期统计表
Tab.10 Statistic of the heights of high-rise buildings and theirs self-vibrating periods in Beijing Basin
根据表9中的回归系数,可计算得到不同周期、不同等效沉积物厚度时的盆地放大系数。图 14表示周期为3 s时盆地对水平加速度反应谱的放大系数的分区结果(为保守起见,其值增加了1倍标准差的大小)。鉴于统计范围内高层建筑的自振周期大多在3 s左右,本文也仅针对3 s周期时的盆地放大系数,初步探讨了北京市高层建筑地震致灾风险水平的分布特征。东部CBD及以东地区的大部分建筑、西二环到西三环之间南半段内的建筑、以及北五环以北地区的部分建筑位于1.5～2.0倍放大区,受到盆地放大效应的影响最为突出,在大地震中可能产生最为严重的地震灾害,是今后地震应急准备和地震救援工作中应着重考虑的对象; 西北部建筑基本位于1.0～1.2倍区,受到盆地放大作用的影响程度相对最小,地震致灾的风险水平相对最低; 其它建筑基本上位于1.2～1.5倍放大区,地震致灾的风险水平介于前两者之间。顺义凹陷和大厂凹陷的中心区域,盆地放大效应非常显著,盆地放大系数最大可至3倍; 此外,昌平凹陷中心区域的盆地放大系数也较大,最高为2.5倍。本文建议,在城市未来规划时,此区域应尽量避免建造自振周期在3 s左右的高层建筑。
图 14 北京市高层建筑分布及3 s周期时的盆地放大系数
Fig.14 Distribution of high-rise buildings and basin amplification factor at period of 3 s in Beijing Basin
(1)通过地震动数值模拟发现:虽然震源因素会在一定程度上造成盆地放大效应的不确定性,但盆地内沉积物的厚度是影响盆地对3～10 s地震动加速度反应谱放大的主要因素。盆地对加速度反应谱的放大系数与盆地内沉积物的厚度之间相关性显著,近地表的第四系和第三系都对盆地放大效应有较大的影响。
(2)建立了3～10 s周期段盆地对加速度反应谱的平均放大系数与等效沉积物厚度之间的函数关系。盆地放大系数随着等效沉积物厚度的增加而增大,随周期的增大而减小。
(3)结合北京盆地内高层建筑的分布和盆地放大系数的分布特征,初步探讨了高层建筑地震致灾风险水平与盆地结构的关系。为北京的城市未来规划、高层建筑的抗震设防以及地震应急救援等提供了科学的借鉴。
