钢管混凝土减震框架的耗能性能与防屈曲支撑的性能密切相关。防屈曲支撑主要是通过核心单元为结构提供刚度和耗散地震能量,在防屈曲支撑长度一定的情况下,核心单元的横截面积是决定其初始刚度的重要因素,因此把核心单元的横截面积x_i作为优化变量,其中i表示第i层。

对于耗能减震结构来说,在结构上设置耗能减震装置是为了消耗输入结构的能量,降低结构的损伤,同时使结构的各项指标满足规范的要求,因此将结构的层间位移角和构件内力作为约束条件,要求钢管混凝土框架各层的层间位移角小于规范规定的层间位移角限值,且结构构件内力小于构件极限承载力。

{θ_i≤θ_lim,

F≤F_lim.(4)

其中:i表示第i层,θ_lim和F_lim分别为层间位移角限值和内力限值。

由于PSO是无约束优化算法,因此需要把约束优化问题转化为无约束优化问题。在本文中,笔者采用“回飞技术”(fly-back mechanism)(黄志斌,2006)处理约束条件。在每次粒子更新位置后,有可能会飞出可行区域,对于飞出了可行区域的粒子,通过强制粒子返回原来的位置,使粒子在可行区域内搜索,这就是“回飞技术”的基本原理。

钢管混凝土减震框架的优化目标是在结构满足《钢管混凝土结构技术规程》(CECS28—2012)要求的前提下,减震框架中防屈曲支撑总截面面积最小,目标函数为

minf(x)=∑ⁿ_i=1x_i.(5)

式中,f(x)为所有防屈曲支撑的截面积之和,x_i表示第i层防屈曲支撑的截面积,n表示总层数。

(1)建立钢管混凝土减震框架的有限元分析模型。本文的分析模型采用杆系模型,梁柱采用平面梁单元,防屈曲支撑采用桁架单元按单斜型铰接于钢管混凝土框架上;

(2)根据具体问题确定优化变量、约束条件以及目标函数,建立钢管混凝土减震框架的优化模型;

(3)运用PSO对钢管混凝土减震框架的耗能构件参数进行优化。

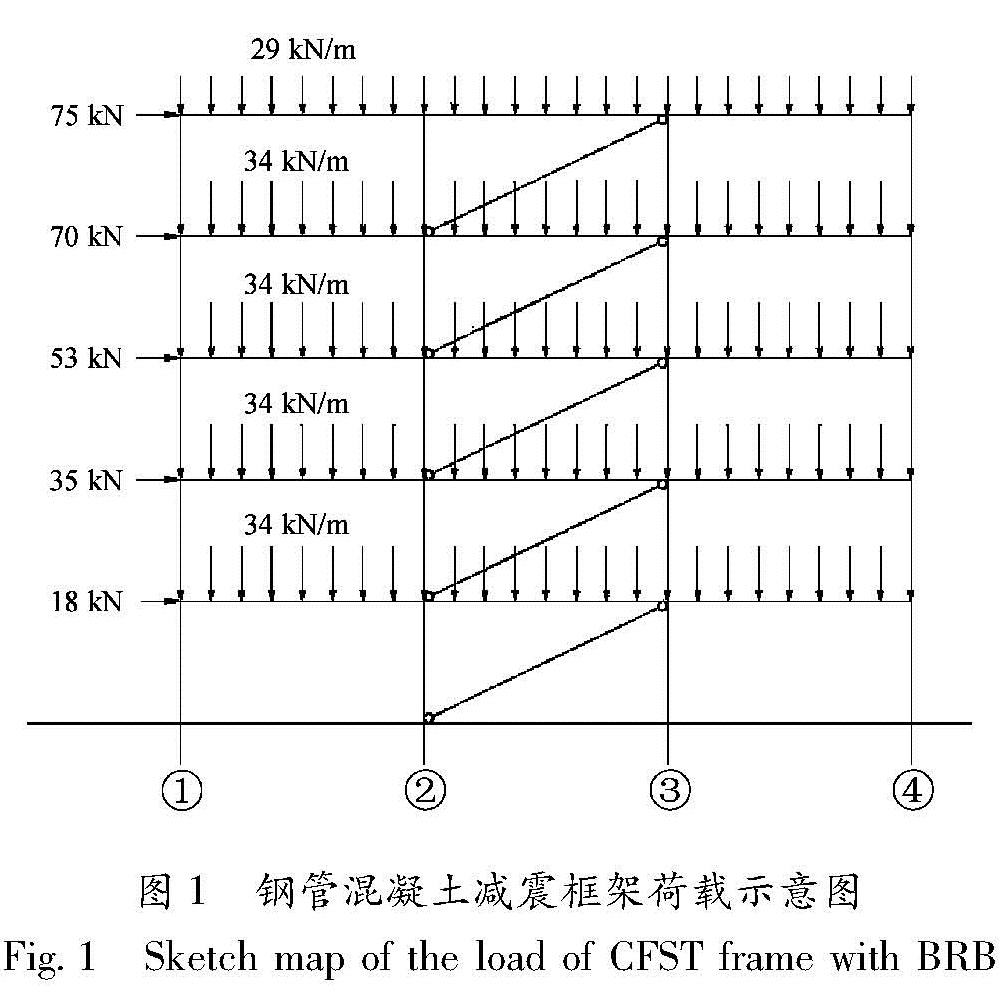
某五层三跨钢管混凝土框架,各跨跨度均为8 m,各层层高4 m,结构抗震设防烈度为Ⅶ度,场地类别为Ⅱ类,设计地震分组第二组,竖向荷载为结构自重和均布荷载的组合值之和。根据底部剪力法计算多遇地震下结构每层承受的水平地震作用,结构的每层荷载如图1所示,钢管混凝土框架的相关参数如表1所示。初步假定在结构每层的中跨布置防屈曲支撑。

图1 钢管混凝土减震框架荷载示意图
Fig.1 Sketch map of the load of CFST frame with BRB

表1 钢管混凝土框架结构参数
Tab.1 Parameters of the CFST frame

各防屈曲支撑的核心单元横截面积为优化变量,防屈曲支撑的截面选择范围为0～0.005 6 m²。

本文中的钢管混凝土减震框架采用杆系模型,梁、柱采用平面梁单元,每个节点有3个自由度:位移u_x、u_v和转角θ 。

钢管混凝土柱的轴压刚度和抗弯刚度采用由叠加法得到的换算刚度(钟善桐,2006),计算公式为

{(E₀A)=E_sA_s+E_cA_c,

(EI)_sc=E_sI_s+0.8E_cI_c.(6)

式中,E_s、E_c分别为钢材的弹性模量和核心混凝土的弹性模量,A_s、A_c、A分别为外钢管面积、核心混凝土面积以及钢管混凝土柱截面积; I_s、I_c分别为钢管的惯性矩和核心混凝土的惯性矩;(E₀A)、(EI)_sc分别为换算轴压刚度和换算抗弯刚度。

根据《钢管混凝土结构技术规程》(CECS28—2012)对框架结构弹性层间位移角的限制要求,结构层间位移角约束限值为1/300,内力限值为弹性阶段抗弯承载力,根据钟善桐(2006)提出的用弯矩—曲率关系曲线的弹性段的极值确定钢管混凝土柱的极限承载力为93.136 kN·m。

对于该算例,PSO参数可选择为:c₁=0.5、c₂=0.5; 惯性权重w由0.9线性递减至0.4; 迭代次数为200次。为了对比PSO的优化结果的优劣性,笔者采用群搜索算法(Group Search Optimizer,简称GSO)对同一模型进行优化,所得出的防屈曲支撑核心单元截面优化结果如表2所示。

表2 优化结果
Tab.2 Results of optimization

从表2可以看出,PSO和GSO的优化结果中,第1～3层设置的防屈曲支撑的核心单元横截面积相同。PSO的优化结果中,结构第4～5层不需要设置防屈曲支撑,而GSO的优化结果中,结构第4层也要设置防屈曲支撑。总的来说,PSO的优化结果中防屈曲支撑核心单元的总横截面积更少。

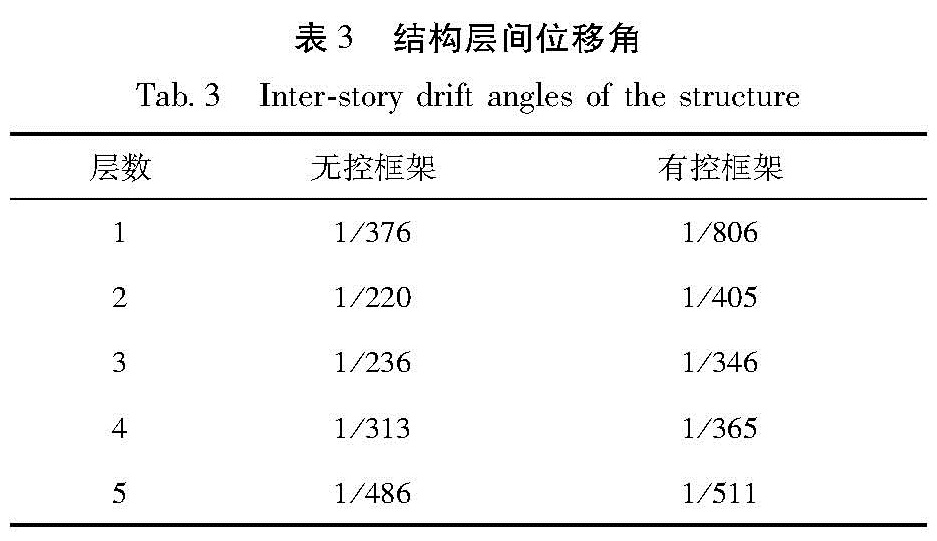
表3为无控框架的层间位移角和设置防屈曲支撑并经PSO优化后结构的层间位移角。从表中可见,无控框架的第2～3层的层间位移角超出了《钢管混凝土结构技术规程》(CECS28—2012)规定的弹性层间位移角限值1/300的要求。结构布置了防屈曲支撑并经过PSO优化后,各层的层间位移角均满足弹性层间位移角限值1/300的要求。

从表2～3可知,经PSO优化后,结构第4～5层的防屈曲支撑面积为零,所以不用设置防屈曲支撑,仅需在第1～3层设置防屈曲支撑。虽然PSO优化结果的防屈曲支撑核心单元横截面积比GSO的优化结果少,但结构的层间位移角均满足规范要求。

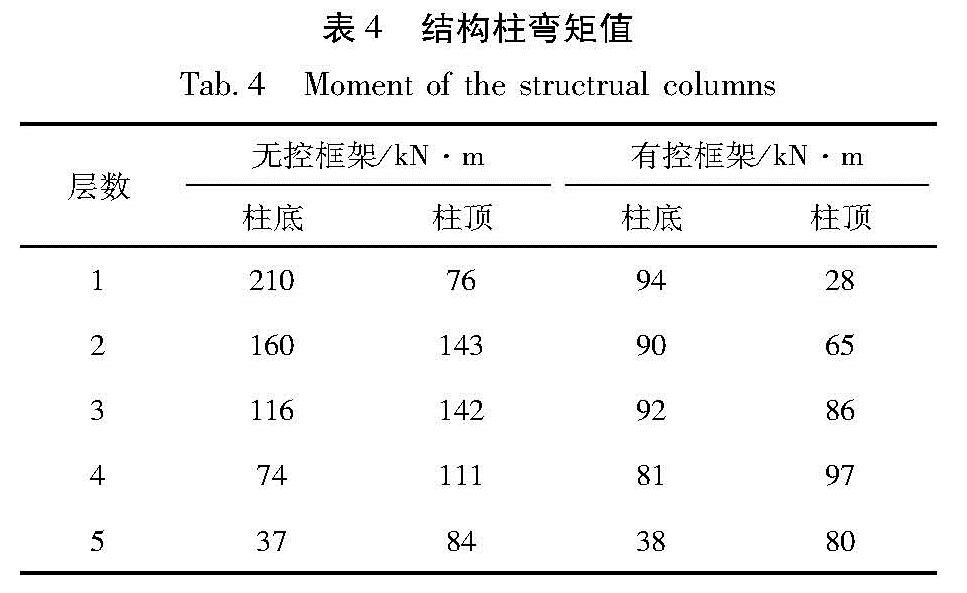
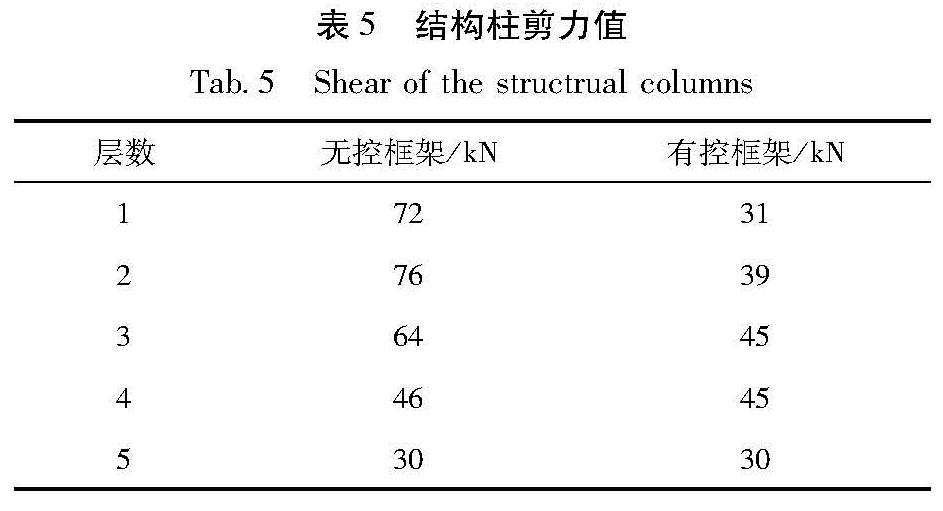
表4～5分别为结构经PSO优化前后的柱弯矩值和柱底剪力值,其中柱为图1中轴2所对应的柱。从表4～5可知,整体而言,设置了防屈曲支撑后,结构柱的最大弯矩值和柱底剪力均得到了明显地减少。由于在第1～3层设置了防屈曲支撑,增加了这三层的抗侧刚度,因此结构的内力发生了重分布,第4～5层的柱底弯矩有所增大,这两层的柱底剪力减少较少,但均满足设计要求。

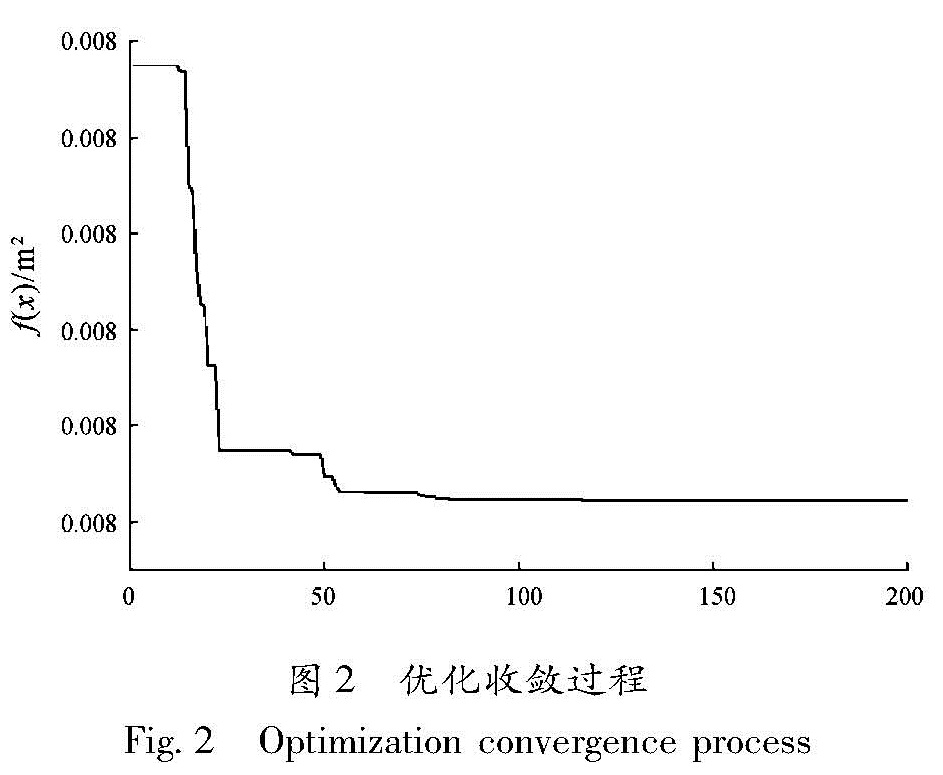
图2为PSO优化收敛过程。从图中可以得出,在程序优化计算前期,由于惯性权重w较大,算

表3 结构层间位移角
Tab.3 Inter-story drift angles of the structure

表4 结构柱弯矩值
Tab.4 Moment of the structrual columns

表5 结构柱剪力值
Tab.5 Shear of the structrual columns

法的全局搜索能力强,粒子迅速向最优解处移动,随着惯性权重w线性递减,算法后期的局部搜索能力增强,进行到122次迭代时,算法已经得到最终解0.003 2 m²,整个优化过程用时19 s。从优化的结果看,与无控结构相比,在设置的防屈曲支撑横截面积总和趋于最小的情况下,经过优化后结构的层间位移角有所降低,满足规范的相关要求。钢管混凝土框架柱的最大弯矩和柱底剪力也得到减少,因此PSO应用于钢管混凝土减震框架优化效果良好,是一种可应用于钢管混凝土减震框架优化的新型方法。

图2 优化收敛过程
Fig.2 Optimization convergence process