工程结构在地震、强风等灾害荷载作用下,会进入弹塑性阶段,结构抗力会发生衰减,呈现出一系列复杂的非线性问题(秦荣,2006)。当结构遭遇较强地震作用时,结构构件将有可能发生屈服、结构刚度发生退化,从而使结构响应迅速增大,甚至造成结构破坏、倒塌(韩建平等,2007)。结构AMD主动控制技术使得结构在外部动力荷载作用下,能主动调整结构参数,从而最优地减小结构振动响应。控制算法作为该技术的核心组成部分,决定着振动控制的稳定性和减振效果的好坏。因此,选择合适的控制算法对AMD系统能否有效减小非线性结构的振动响应是极为重要的。

最小控制综合(MCS)算法最早由Stoten和Benchoubane(1990a,b)提出,通过对操纵器、蓄水库装置进行仿真、试验研究,证明了MCS算法在系统参数变化、外部干扰不确定以及系统非线性的情况下也能达到很好的控制效果; Stoten和Gomez(2001)运用MCS算法控制振动台,证明了MCS算法通过自适应增益的实时调整,可以有效地处理振动台运行过程中出现的非线性情况,提高振动台的精度。

基于以上研究成果,本文将MCS算法应用于AMD控制系统中,系统研究了该控制系统对非线性结构的控制效果。本文比较了刚度退化结构与线性结构的地震反应; 用MCS算法来控制AMD系统,采用拉格朗日法推导了地震作用下结构自适应控制的基本方程; 为了验证MCS算法控制AMD装置的有效性,在小型振动台上对安装AMD系统的刚度突变结构进行试验研究。

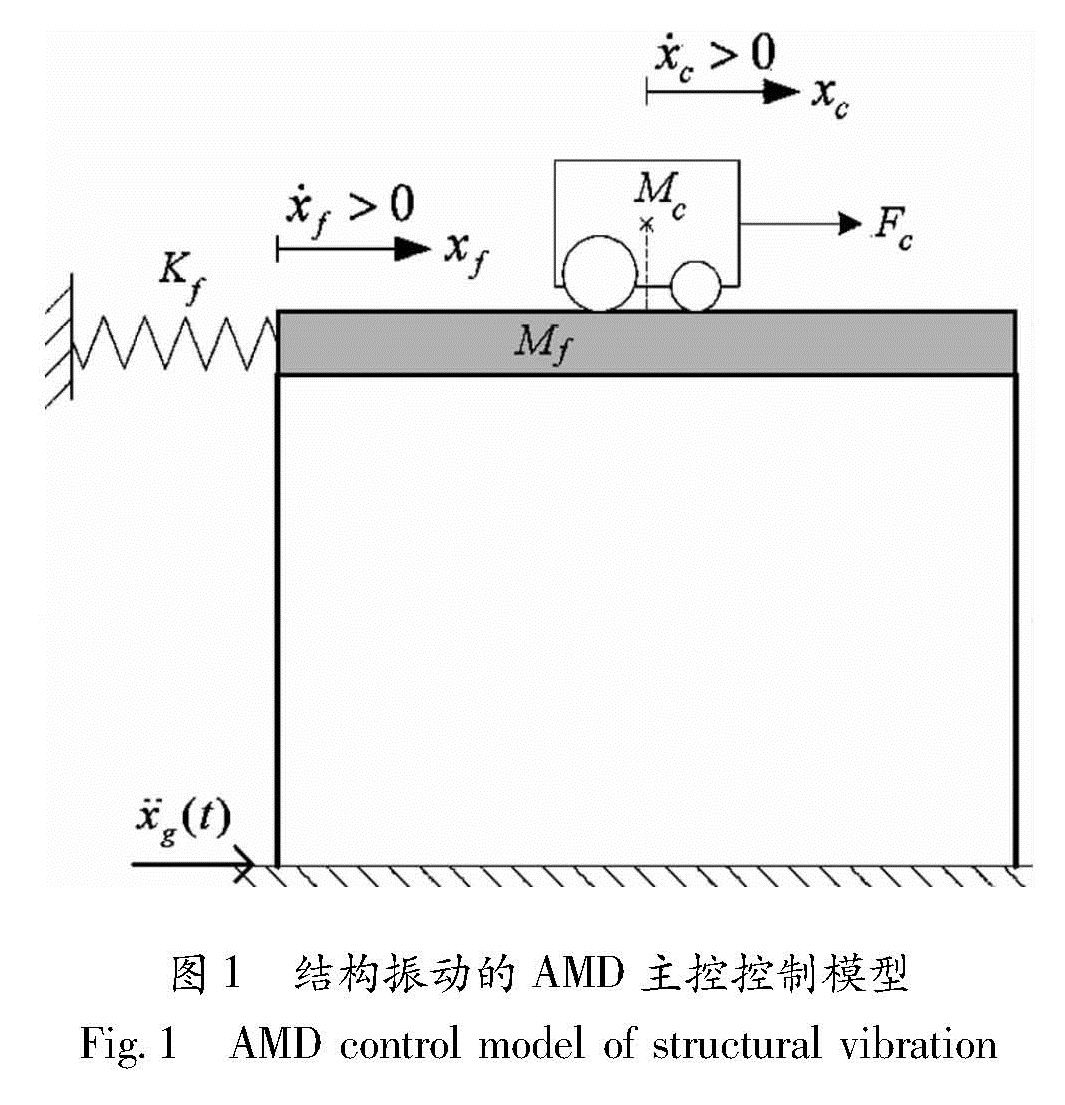
本文研究对象是安装AMD控制系统的单层结构模型,模型简图如图1所示,具体参数如表1所示。

表1 AMD装置控制的结构模型参数
Tab.1 The model parameters of the structure under AMD control

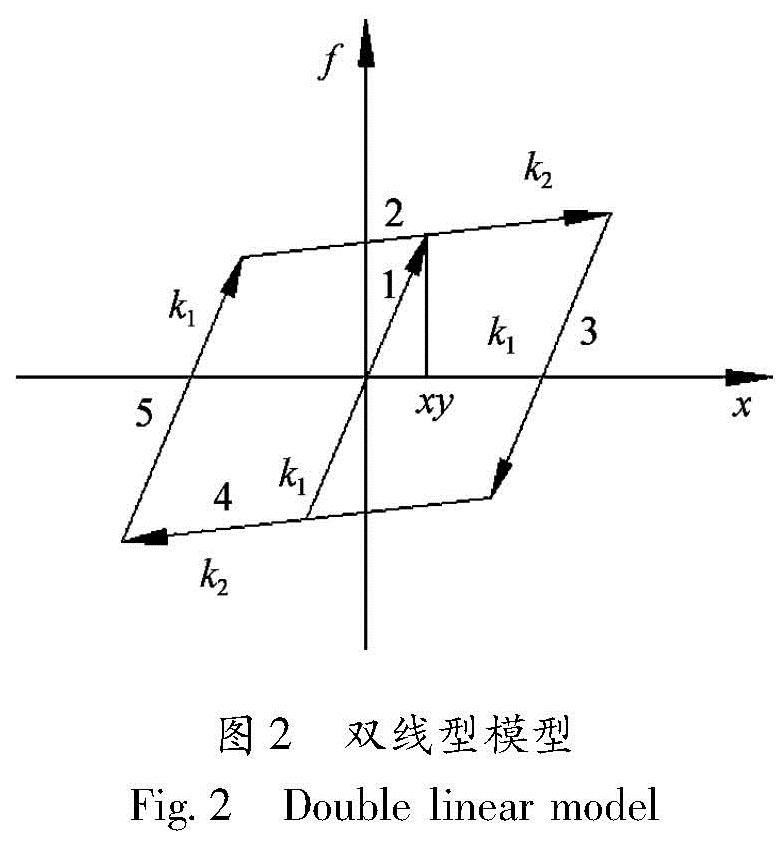
首先采用理想不退化双线型模型建立结构刚度的退化模型(彭凌云,2004),如图2所示。该模型的加载刚度和卸载刚度均为结构初始刚度,结构初

图1 结构振动的AMD主控控制模型
Fig.1 AMD control model of structural vibration

图2 双线型模型
Fig.2 Double linear model

图3 无控结构刚度的时程曲线(a)和滞回曲线(b)
Fig.3 The time history(a)and hysteretic(b)curves of uncontrolled structure stiffness

图4 无控结构位移响应的时程曲线
Fig.4 The time history of uncontrolled structural displacement response

从图3可以看到,结构恢复力与位移之间表现出明显的不退化双线型恢复力模型,说明仿真过程是准确无误的; 图4对比了线性无控与刚度退化时的结构位移响应,从图中可以看到,由于没有减振装置,结构刚度从第三秒开始就处于屈服退化状态,结构响应迅速增大并持续保持在较大范围内波动,这会威胁到结构的安全,需要采取减振措施对结构响应进行控制。

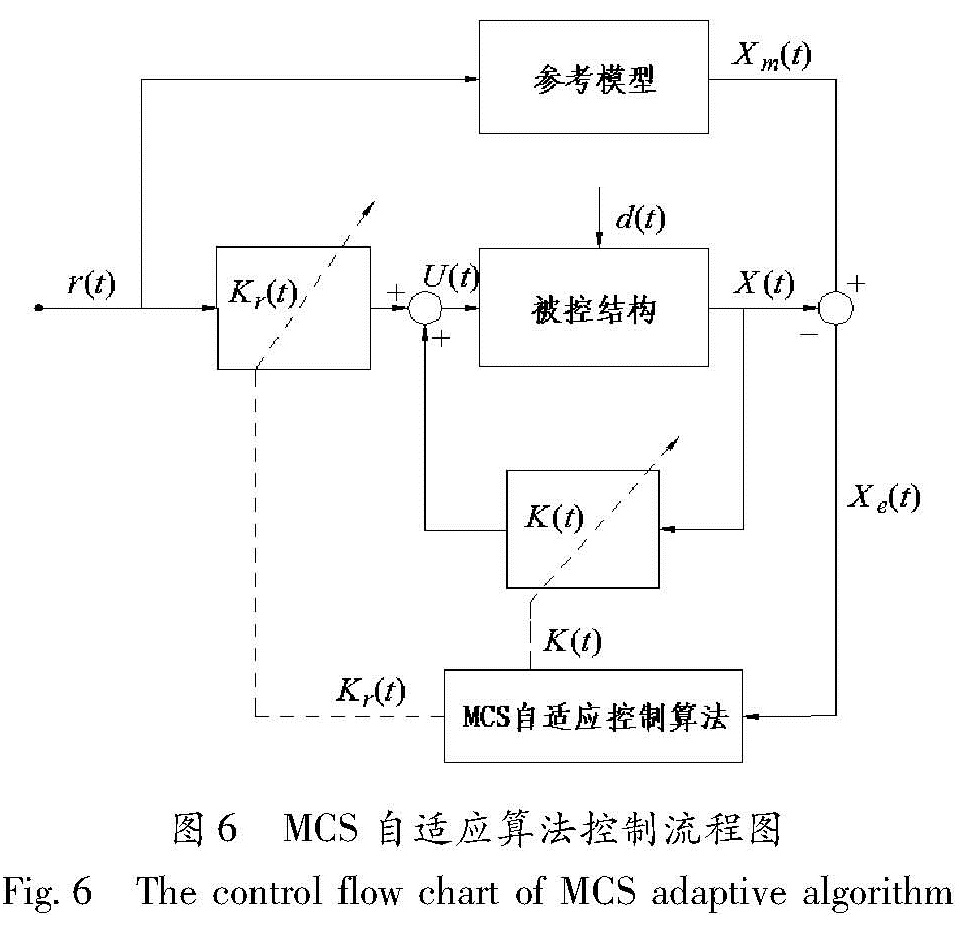
首先阐述AMD系统控制的原理及公式。结构AMD主动控制系统由传感器、控制器和作动器组成,其原理如图5所示。在整个控制过程中,需要实现控制力可以实时改变和受控结构的实际振动响应与参考模型响应保持一致这两个目标(欧进萍,2003),参考模型MCS自适应控制算法可以实现上述目标,其原理如图6所示。受控结构在外部激励d(t)作用下输出响应为X(t),参考模型在外部激励r(t)作用下输出响应为X_m(t)。 将X_m(t)作为目标响应,X_e(t)为X(t)与X_m(t)产生的偏差,它会驱动自适应控制器,计算当前时刻的自适应增益K(t)和K_r(t),从而实时计算出主动控制力U(t)。将U(t)将施加到受控结构上,会使得结构实际响应跟踪目标响应,即X(t)=X_m(t),从而实现了控制目标。

在地震作用下,结构振动的AMD主动控制模型如图1所示,其拉格朗日方程为(卢圣治,2004)

d/(dt)(L)/( q^·_α)-(L)/(q_α)=Q_qα.(1)

其中,L为系统的拉格朗日函数,L=T-V,V是系统的势能,T是系统的动能; q_α是广义坐标,本文广义坐标取x_f和x_c; Q_qα是对应广义坐标上的广义力。

在绝对位移坐标系下,地震作用的地面位移为x_g(t),由式(1)可以得到:

((M_cr²_mp+J_mK²_g)(d²)/(dt²)x_c)/(r²_mp)+M_c(d²)/(dt²)x_f

=F_c-B_eqd/(dt)x_c-M_cx^¨_g(t).(2)

图5 结构AMD主动控制系统
Fig.5 AMD control system of the structure

图6 MCS自适应算法控制流程图
Fig.6 The control flow chart of MCS adaptive algorithm

=-(M_c+M_f)x^¨_g(t).(3)

其中,J_m为小车电机转动惯性矩; K_g为小车齿轮传动比; r_mp为小车电机齿轮半径; B_eq为小车等效粘滞阻尼; C为结构阻尼。

定义结构的主动控制力U=F_c,状态向量X^T=[x_c(t)x_f(t)d/(dt)x_c(t)d/(dt)x_f(t)],系统在地震作用下的状态方程可以由式(2)、(3)得到:

X^·=AX+BU-D_gx^¨_g(t).(4)

其中,d(t)=x^¨_g(t),对于采用MCS控制算法的结构AMD控制系统,主动控制力U可由式(5)计算得到:

U(t)=K(t)X(t)+K_r(t)r(t).(5)

其中,r(t)为参考输入, 取r(t)=K_d·d(t)=K_d·x^¨_g(t), 0<K_d<1, K(t)、 K_r(t) 为自适应增益,可通过式(6)计算得到:

K(t)=∫ ^t∫₀αy_e(τ)X^T(τ)dτ+βy_e(t)X^T(t),

K_r(t)=∫ ^t∫₀αy_e(τ)r^T(τ)dτ+βy_e(t)r^T(t).(6)

其中,比例因子α>0,β≥0; y_e(t)是系统输出误差信号,可由式(7～8)计算得到:

y_e(t)=C_eX_e(t).(7)

X_e(t)=X_m(t)-X(t). (8)

其中,C_e是输出矩阵; X_e(t)是参考模型输出与被控模型输出的误差; X_m(t)是参考模型的输出响应。这几个参数可通过以下参考模型的状态方程求得:

X^·_m(t)=A_mX_m(t)+B_mr(t);(9)

C_e=diag(C_ei); C_ei=[ω_i 1];(10)

A_mi=[0 1

-ω²_i -2ξω_i]; B_mi=[0

ω²_i];(11)

A_m=diag(A_mi); B_m=diag(B_mi). (12)

其中,ω_i为结构第i阶自振频率(i=1,2,…,n); ξ为结构阻尼比。

该试验在武汉理工大学完成,试验装置由小型振动台、一层剪切型钢框架结构和AMD控制装置组成,加拿大Quanser公司研发了该设备。为了实现结构的刚度突变,先对结构采用增加橡皮筋斜撑的方法来增加结构刚度,如图7所示。当结构

图7 加橡皮筋的试验结构
Fig.7 Experimental structure of the added rubber bands

使用压缩后的El Centro波作为地震激励驱动小型振动台,地震波的峰值加速度是0.5 g,持续时间是13.4 s,取实测台面加速度作为d(t),采用降低地震能量方法建立参考模型(张凯静等,2010),地震能量调节增益K_d=0.75,采用MCS自适应算法对AMD装置实施控制,输出矩阵取C_e=[ω₁ 1]=[17.8 1], α=100, β=10。

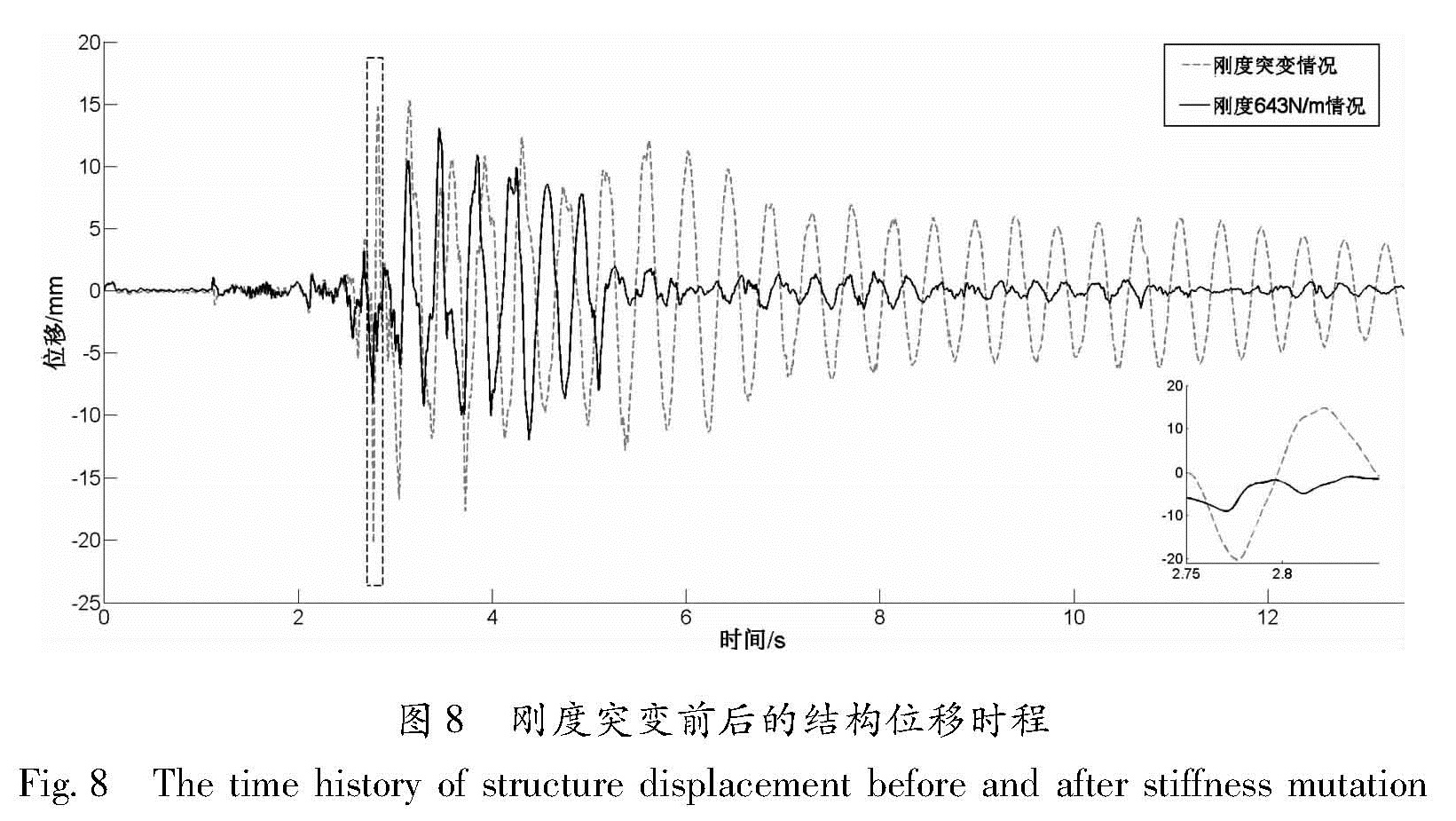
图8显示了剪断橡皮筋前后结构的位移响应。从图中可以看出,在地震持续时间为2.8 s时,皮筋被剪断,结构的刚度从643 N·m^-1迅速减小到500 N·m^-1,相对于不剪断皮筋情况结构顶点的最大位移从13 mm增大到20 mm。特别是在剪断皮筋的瞬间,结构的最大位移从9 mm迅速突变到20 mm,增大了约120%。图9显示了刚度突变情况下无控、MCS算法控制的结构的位移响应。从图中可以看出,采用MCS算法的AMD系统可以有效地减小结构的振动响应,具体如表2所示。其中,x_f、x^¨_f分别是结构顶部相对于地面的位移和加速度; mag_xf是结构位移傅里叶幅值; x_f,RMS是结构位移均方根值,表示在地震作用持续时间内x_f各瞬时值的平方的平均值的平方根。在地震持续时间为2.8 s皮筋被剪断的瞬间,MCS算法可以将结构位移从无控状态的20 mm减小到7 mm。这是因为MCS自适应算法是根据结构响应与参考模型响应的误差反馈实时地改变控制增益,因此当结构响应发生突变时,MCS算法也可以迅速增大控制增益来得到较大的控制电压,从而可以很好地减小结构振动响应。

表2 地震作用下的试验结构振动响应
Tab.2 The vibration responses of experimental structure under earthquake

图 10比较了参考模型输出的位移响应和实际结构的位移响应。从图中可以看到,即使结构刚度发生突变,实际位移也能够很好的逼近参考模型的输出响应,达到预期的减振效果。

研究了MCS自适应控制算法对非线性结构的AMD主动控制,并完成了刚度发生突变的单自由度结构的振动台试验。仿真和试验结果表明:MCS算法是一种优良的自适应控制算法,将它应用到结构AMD控制系统中,可以有效地减小结构响应。在结构发生刚度突变时,MCS算法通过自适应参数的实时调整仍能有效地控制AMD装置,使结构实际输出响应与参考模型输出保持一致,达到预期的减振效果。

图8 刚度突变前后的结构位移时程
Fig.8 The time history of structure displacement before and after stiffness mutation

图9 刚度突变情况下无控和采用MCS算法AMD控制的结构位移时程
Fig.9 The displacement time history of structure controlled by AMD using MCS algorithm or without control in the case of stiffness mutation

图 10 刚度突变情况下参考模型输出位移与实际结构位移时程对比
Fig.10 Comparison of time histories between output displacement of reference model and displacement of actual structure in the case of stiffness mutation