地铁隧道盾构开挖引起土体应力的重新分布,产生地表沉降,对周围建(构)筑物、地下管线等势必造成一定的损害,严重时会出现坍塌、变形等现象。因此,在地铁隧道施工前期,对地表变形进行准确的预测很有必要。Peck在对大量实测数据进行分析和研究的基础上,于1969年提出了估算开挖隧道地表沉降的预测公式,即Peck公式(潘海泽等,2010),该公式已成为目前应用最为广泛的方法。但是,由于地域差异性引起的地质条件的差别会对预测值的准确性产生较大的影响,Peck公式只是基于某一地区的研究,因此,误差不可避免。本文基于长春地铁的实测数据和地质情况,以Peck公式为基础,进行回归分析,得到回归拟合后的沉降曲线,并对Peck公式进行修正,研究其在长春地区的适用性,并指导工程实践,预防地铁施工事故的发生。

长春地铁二号线文化广场—解放大路区间(简称WJ)工程,起讫里程为K20+730.976～K21+862.843,区间全长1 385.443 m。本文选取测点AWDBY-WJ-940所处区段,埋深12.6 m,线间距13 m,采用单洞单线盾构施工。监测点布置情况如图1所示。

图1 监测点布置图

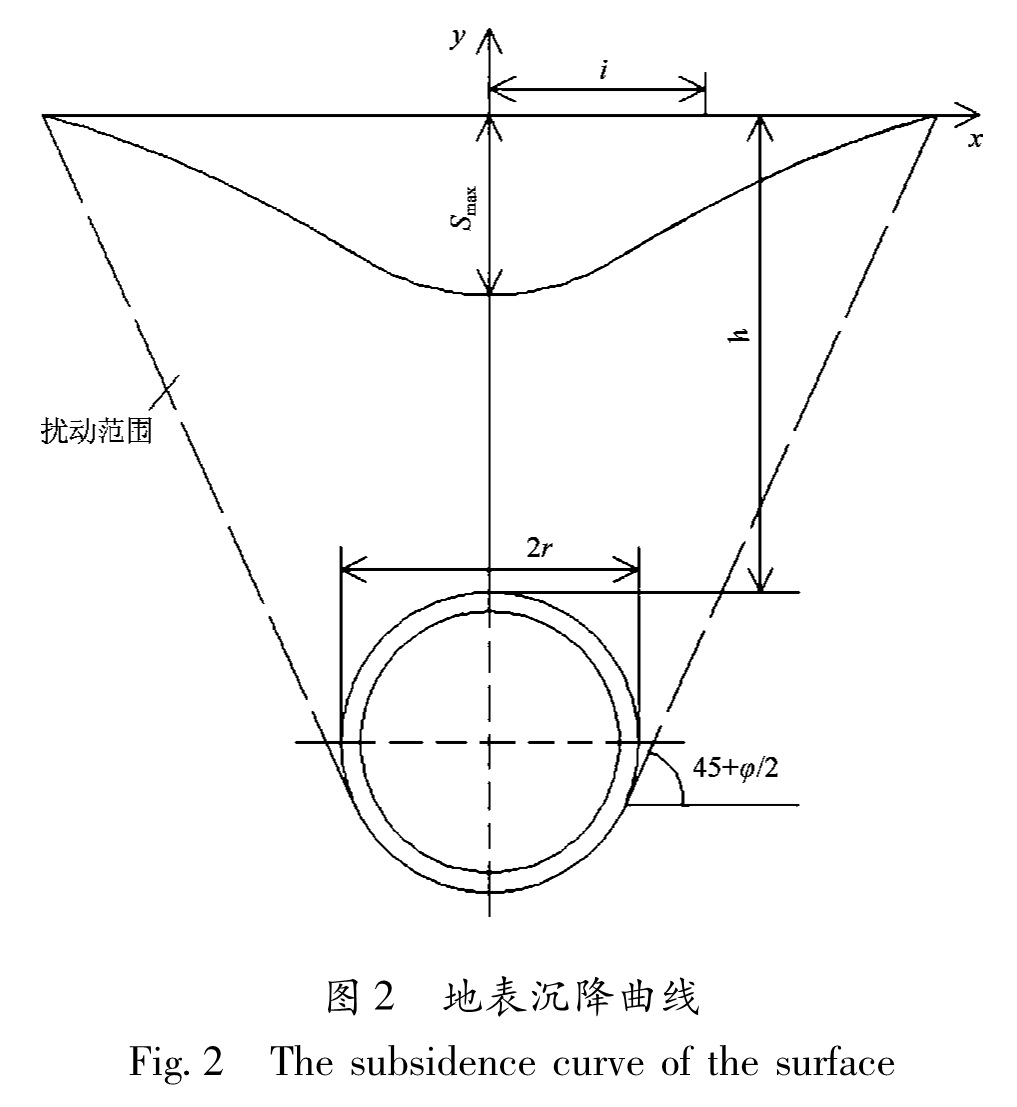
1969年,Peck在搜集大量地表沉降观测数据的基础上,对这些数据进行了详尽的分析,从而提出地表沉降槽近似符合正态分布曲线的理论学说(陈军等,2005):地面沉降槽的体积等于隧道施工中地层损失的体积,而且假设施工横断面上地面沉降曲线(图2)的形状和正态分布曲线的形状是一样的(宋克志等,2004)。根据这个理论,Peck提出了地表沉降的预测公式:

S(x)=S_maxexp((-x²)/(2i²)). (1)

S_max=(V₁)/((2π)^1/2i)≈(V₁)/(2.5i).(2)

式中,S_x是距离隧道中心线横向距离x处的地表沉降值(单位:mm); x是距离隧道中心线的水平横向距离(单位:m); S_max是地表的最大沉降值(单位:mm); V₁是盾构隧道单位长度的地层损失量(单位:m³/m); i是沉降槽的宽度。依据Reilly和New(1982)在英国伦敦地区的工程经验,沉降槽的宽度i和隧道的深度h之间存在以下线性关系(韩煊,李宁,2007):

i=Kh.(3)

式中,K是沉降槽的宽度系数,主要取决于土体自身的物理性质。根据英国伦敦地区的工程实践经验(韩煊等,2007):对于无粘性土,K取0.2～0.3; 对于硬粘土,K取0.4～0.5; 对于软的粉质粘土,K取0.7。

图2 地表沉降曲线

图2中,φ为土体的内摩擦角(单位:(°)); h为覆盖土层的厚度(单位:m); r为盾构半径(单位:m)。

本文不考虑水的影响,故地层损失与最大位移之间的关系可通过对式(1)积分得到:

S_max=(0.313V₁D²)/i.(4)

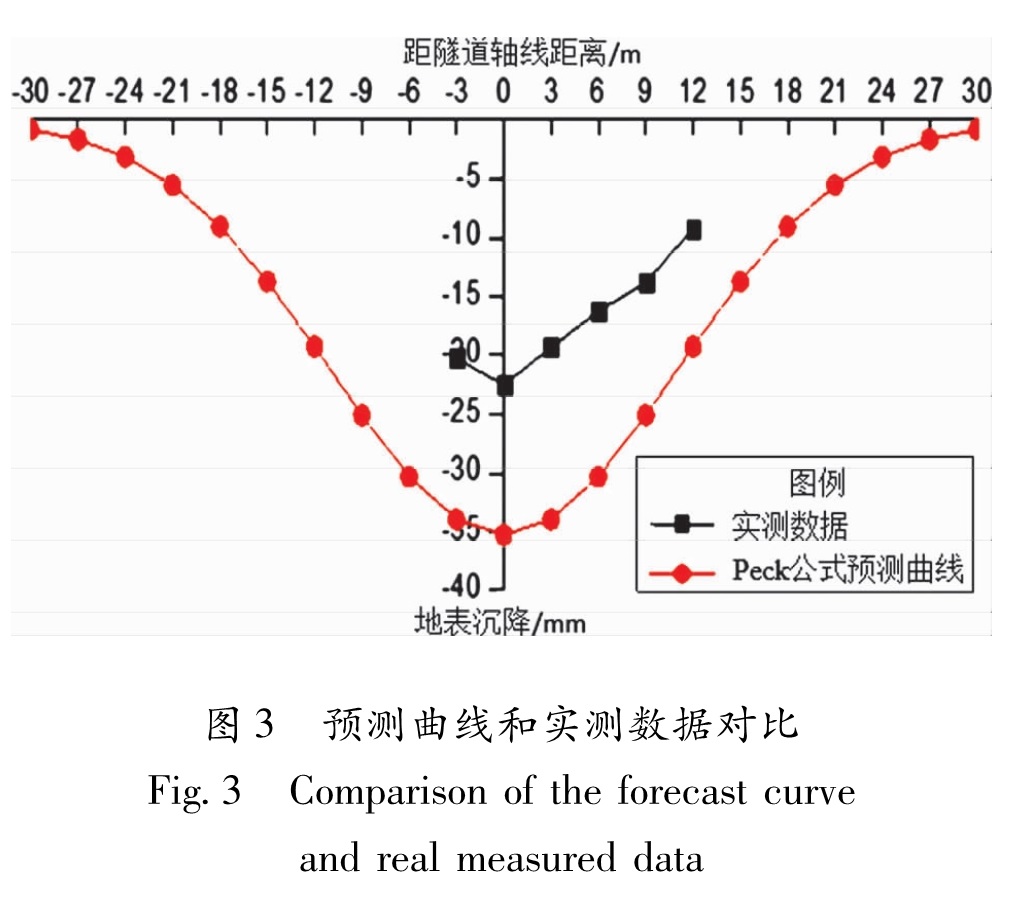
通过上述公式计算得到距隧道中心线横向距离x处的地表沉降值,并绘制出Peck预测曲线和实测数据曲线(图3)。

图3 预测曲线和实测数据对比

and real measured data

由图3可以看出,Peck预测曲线和实测数据曲线之间存在较大的误差,故需对Pcek公式进行回归拟合。

首先对原始Peck公式即式(1)进行对数运算,得到如下公式(严健等,2015):

lnS(x)=lnS_max+1/(i²)+(-(x²)/2).(5)

将lnS(x)和-x²/2作为线性回归的变量,将lnS_max作为线性回归的常数项,将1/i²作为线性回归的线性系数。整个回归过程如下(胡斌等,2012):

S_xx=∑((-x²_i)/2)²-1/n(∑(x²_i)/2)².(6)

S_xy=∑[((-x²_i)/2)lnS(x_i)]

-1/n∑((-x²_i)/2)∑lnS(x_i).(7)

S_yy=∑ln²S(x_i)-1/n[∑lnS(x_i)]².(8)

b=(S_xy)/(S_xx).(9)

a=lnS(x_i)^--b(-x²/2)^-.(10)

线性回归处理以后,得到如下的理论公式:

lnS(x)=a+b×(-(x²)/2). (11)

式中,x_i为所选择的样本中第i个样本点与隧道轴线距离的代数值; n为所选择的样本点的个数; a为线性回归处理以后的常数项; b为线性回归处理以后的线性系数。

对上述公式进行计算,可以得到线性回归后S_max和i的理论计算公式:

S_max=exp(a).(12)

i=1/(b^1/2).(13)

线性相关系数R是用来检验回归分析处理后得到的Peck理论计算公式的线性相关关系程度。线性相关系数R的计算公式如下(姚爱军等,2010):

R=(S_xy)/((S_xx)^1/2×(S_yy)^1/2).(14)

若依据上式运算得到R>r_0.01(n-2),则得出线性回归后Peck公式的线性相关关系高度显著;

若依据上式运算得到r_0.01(n-2)>R>r_0.05(n-2),则得出线性回归后Peck公式的线性相关关系显著。

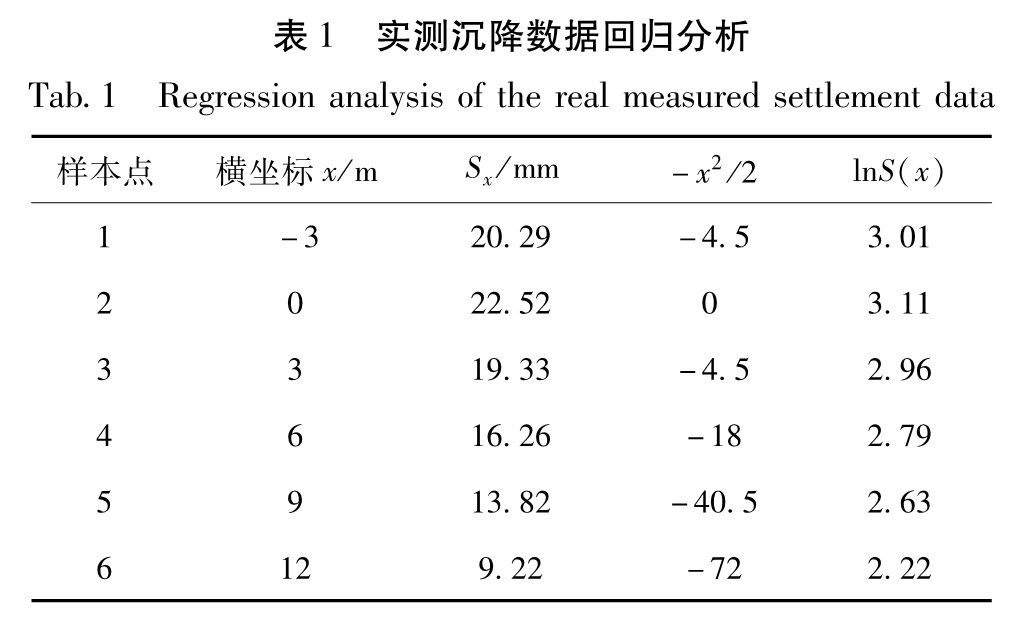
按上述步骤计算WJ区间AWDBY-WJ-940测点的地表沉降数据,回归分析处理以后的结果如表1所示。

根据表1中的数据,并结合上述回归分析公式,可计算得出:S_xx=3 945.38,S_xy=45.43,S_yy=0.53; 再由式(9)、(10)计算得出:a=3.05,b=0.011 5; 从而得到回归后的线性函数:lnS(x)=3.05+0.011 5×(-(x²)/2); 由式(12)、

表1 实测沉降数据回归分析

(13)计算得出:S_max=21.22,i=9.32,进而可以绘制拟合后的Peck曲线,并将其与地表沉降实测数据和Peck预测曲线对比(图4)。

线性相关系数由式(14)计算得到:R=0.990>r_0.01(4)=0.917,由此判断回归函数线性相关关系高度显著。

图4 实测数据、预测曲线和拟合曲线对比

forecast curve and fitting curve

由图4可以看出,拟合后的曲线与实测数据基本吻合,能够较好地反映地表沉降的实际概况,可以用于地表沉降预测。但Peck公式预测曲线与实测数据、拟合曲线存在比较大的数值偏差,有必要对Peck理论公式进行修正。

依据上述的理论分析,运用Peck理论公式,在公式中添加两个修正系数α和β,得到如下的修正公式(段绍伟等,2015):

S(x)=αS'_maxexp((-x²)/(2(βi')²)).(15)

式中,α为地表最大沉降修正系数; β为沉降槽宽度系数修正系数; S'_max为Peck理论公式原始预测的地表沉降最大值(单位:mm); i'为Peck理论公式原始预测的沉降槽宽度系数(单位:m)。

转换为线性函数:

lnS(x)=ln(αS'_max)+1/((βi')²)×(-(x²)/2). (16)

以ln(αS'_max)为回归分析后的常数项,以1/((βi')²)为回归分析后的线性系数进行回归处理(郭延华,吴龙海,2013),可得到两个修正系数的计算公式:α=(exp(a))/(S'_max), β=1/(i'b^1/2)。根据已求解的S'_max和i'计算得:α=0.60,β=0.85。选择不同的工作截面可以计算出不同的修正系数,对大量的工作断面进行参数分析,可以得出长春地区地铁盾构施工断面修正系数的分布特点。

表2 修正系数分布

由表2可以看出,当地表最大沉降修正系数α位于0.6～0.9之间时,占80%; 当沉降槽宽度系数β位于0.5～0.9之间时,占82%。结合图4的分析结果,不难得出,修正后选取的α、β值能够更加准确地进行Peck理论公式的地标沉降预测。

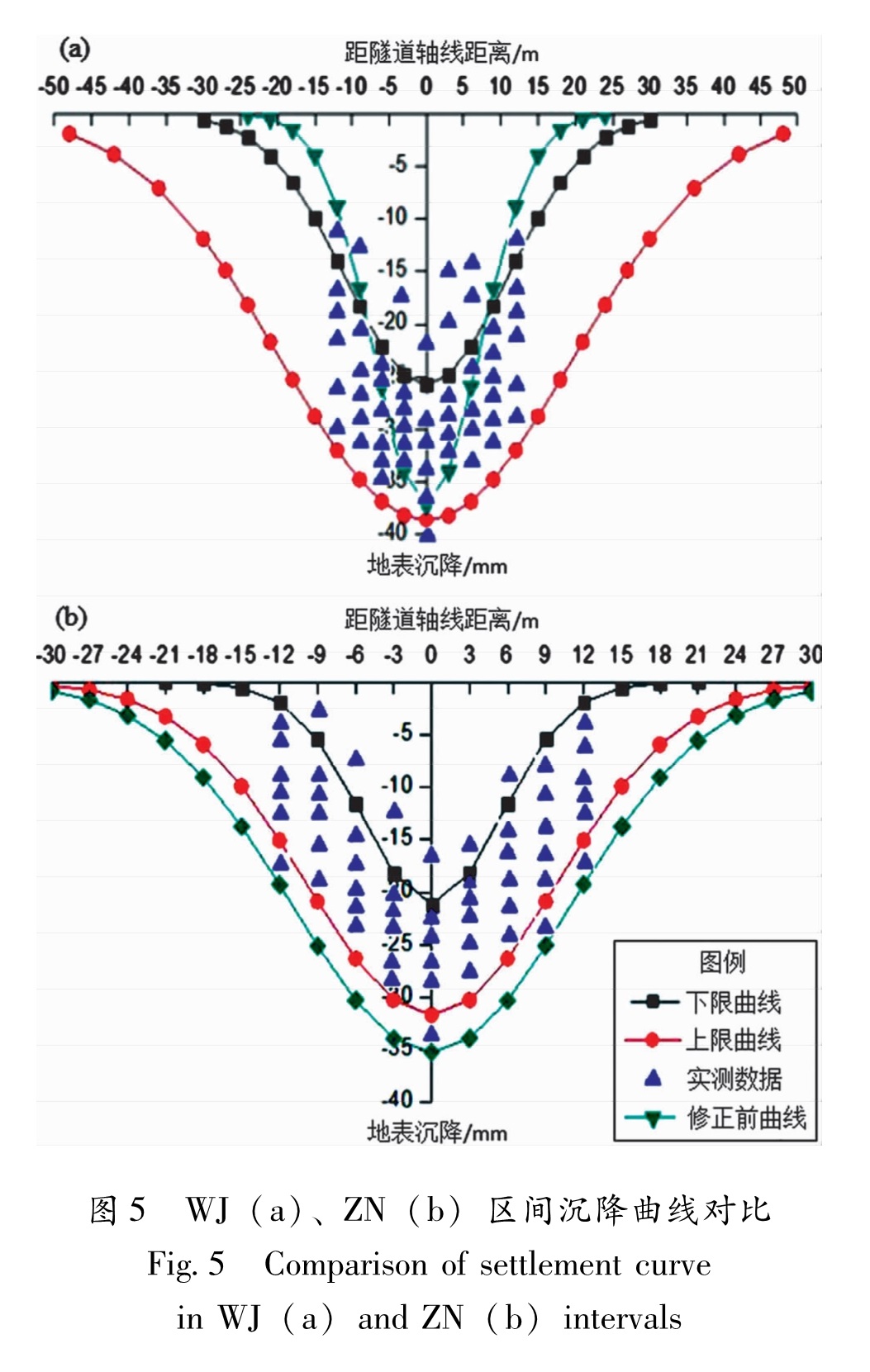
将α、β的下限值和上限值分别作为修正系数运用于两个典型的区间工程(WJ区间和自由大路—南湖大路区间(简称ZN),同时,将得到的Peck公式预测曲线(简称上限曲线和下限曲线)与实测数据进行对比。

由图5可以看出,绝大多数实测数据位于上限曲线和下限曲线之间,极个别实测数据位于下限曲线之下,少量实测数据位于上限曲线之上。因此,可以将修正后的Peck公式用来预测地表沉降,其预测效果明显优于原预测曲线。

图5 WJ(a)、ZN(b)区间沉降曲线对比

in WJ(a)and ZN(b)intervals

本文以长春地铁的施工监测数据为基础,利用修正的Peck公式对地表沉降进行预测,得出以下结论:

(1)运用Peck理论公式,结合长春地铁的工程地质和水文地质概况,计算得出了地铁盾构开挖地表沉降的最大理论值,并且,工程实测的数据显示其地表沉降的横向分布近似为一条正态分布曲线。

(2)当地表的最大沉降修正系数α位于0.6～0.9之间,沉降槽的宽度系数β位于0.5～0.9之间时,计算得到的Peck理论公式修正曲线与工程实测数据曲线相对吻合,其预测的效果明显比原始Peck理论公式预测曲线的准确程度高,更能反映地表沉降的变化趋势。

(3)充分说明了可以将Peck公式用于长春地铁施工沉降的预测,但需要对原始公式中的地表最大沉降和沉降槽宽度进行修正,修正以后的Peck公式的预测结果与实际施工沉降基本吻合,能够很好地指导工程实践。