基金项目:国家自然科学基金创新群体项目(51121005)、国家自然科学青年基金项目(51408099)和博士后科学基金(2014M560210,2015T80253)联合资助.
(Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian 116024,Liaoning,China)
decentralized control; bilinear matrix inequality; double homotopy; time delay; large scale civil structures
备注
基金项目:国家自然科学基金创新群体项目(51121005)、国家自然科学青年基金项目(51408099)和博士后科学基金(2014M560210,2015T80253)联合资助.
土木工程结构具有尺度大、结构复杂的特点,在结构主动反馈控制中,结构的大尺度会导致反馈的时滞大问题,从而影响甚至恶化结构的振动反应,对结构安全不利。为了解决该问题,针对大尺度土木结构反馈过程的时滞问题提出了H∞分散控制方法。由于分散控制器矩阵的块对角形式,现阶段还没有一个具体的理论或现成的软件来解决BMI这个问题。在离散时域内提出了双同伦法将此BMI近似线性化为线性矩阵不等式,并将集中控制器逐步转化为分散控制器。最后通过6层框架数值算例进行了验证,结果表明该方法可以有效地减小结构反馈控制中的时滞问题,保证了
The civil engineering structure has the characteristic of large scale and complex structure. In the active feedback control of the structure,the large scale of the structure would lead to the big problem of the feedback time-delay,which would affect and worsen the vibration response of the structure,and has an adverse effect on the safety of the structure. To solve the above problems,we proposed the decentralized H∞ control method. Because of the special block-diagonal patterns on decentralized controller matrices,there is no specific theory or off the shelf software to solve the bilinear matrix inequality(BMI)problem. So,we proposed a double homotopy method to solve the BMI problem in discrete time domain. The method approximates the BMI problem to a series of linear matrix inequality(LMI)problems along two homotopic paths,and gradually deforms a centralized controller to a decentralized controller. The proposed method is validated numerically with a six-story building example. The result shows that the proposed double homotopy method could reduce effectively the time lag problem in the feedback control of the structure,and ensure the control effect.
引言
结构振动控制分为被动控制、主动控制、半主动控制和混合控制。在主动控制中,需要由传感器、驱动器、控制器和结构组成闭合回路,从而实现反馈控制。反馈的实时性是主动控制效果好坏的关键。然而,对于大尺度土木工程建筑物,反馈过程中会出现大时滞问题,从而影响控制效果,尤其对于无线传感器的数据传输,结构尺度大导致的长距离传输会影响数据的实时性,数据量大也同样会导致因计算时间长出现的时滞问题。
分散控制是解决反馈时滞问题的一种有效手段。分散控制不同于集中控制,是将反馈控制系统分为几个子系统,每个子系统在反馈过程中仅接受部分传感器反馈信息数据,从而减小传输距离与传输数据量(Sandell et al,1978; Siljak,1991)。虽然分散控制已经应用于输电网络、空间系统和经济系统等众多行业中(Siljak,1996),但土木工程结构中的分散控制却在最近几年才逐渐被关注。Lynch和Law(2002)改进了分散LQR控制方法,并提出了基于市场机制的分散控制,从而解决土木结构大尺度的问题。Xu等(2003)针对斜拉桥进行减振控制,提出了分散锚索控制方法。Swartz和Lynch(2006)将冗余Kalman状态估计器应用于分散结构控制系统中。Rofooei和Monajemi-Nezhad(2006)研究了不同反馈形式的控制。Lu等(2008)提出了分散滑模控制,并对带有磁流变阻尼器的钢框架进行了振动台实验。Ma等(2008)进行了分散鲁棒控制研究。Loh和Chang(2008)比较了集中控制及各种形式的分散控制。最近,分散控制中考虑到了控制器计算和数据传输导致的时间延迟(Wang et al,2009,2011)。普遍来说,控制器需要的传感器数据越多,时间延迟就越大。时间延迟作为系统性能的一部分是可以被测量和计算得到的,例如无线反馈控制系统(Wang et al,2007)。考虑到控制过程中的反馈时滞问题,本文在离散时域中提出了一个新的H∞分散动力反馈控制方法。
有界实引理是求解H∞控制器矩阵的有效方法(Gahinet,Apkarian,1994)。控制器矩阵在有界实引理中被约束于双线性矩阵不等式(Bilinear Matrix Inequality,简称BMI)中(VanAntwerp,Braatz,2000)。当控制器矩阵不存在特殊结构形式时,这个双线性矩阵不等式约束是可以通过投影引理转化为多个线性矩阵不等式(Linear Matrix Inequality,简称LMI)约束来进行求解的。然而,分散控制要求控制器矩阵是具有分散块对角结构形式的,这种形式在有界实引理中是难以转化为线性矩阵不等式约束的,从而形成了非凸的优化问题。目前还没有有效的解决方式来处理该问题。虽然来自PENOPT公司的PENNON(PENalty methods for NONlinear optimization)软件包是用来解决此非凸优化问题的,但该方法仍然是不成熟的,需要进一步改进(Kocvara,Stingl,2003)。Wang(2011)将连续时域的同伦方法进行一定修改应用于离散时域中。Mehendale和Grigoriadis(2008)针对无时滞问题的连续时域系统,提出了基于双同伦方法的H∞分散控制方法。本文考虑了土木工程中反馈时滞问题,提出了基于双同伦方法的离散时域H∞分散控制方法。最后通过6层结构算例对提出的方法进行了验证。
Fig.1 Frame chart of the structural control system1 问题描述
考虑带有时滞的结构控制系统如图1所示。根据Wang(2011)的推导,在离散时域中连接结构系统和带有传感器噪声干扰的时滞系统得到离散时域下的开环系统如下:
{x[k+1]=Ax[k]+B1w[k]+B2u[k],
z[k]=C1x[k]+D11w[k]+D12u[k],
y[k]=C2x[k]+D21w[k]+D22u[k].(1)
其中, 系统输入w=[w1 w2]T∈Rnw×1,包含外界激励w1和传感器噪音w2。u∈Rnu×1表示控制力向量。开环系统状态向量x∈RnOL×1包含结构系统状态向量xS∈R2n×1,带有传感器噪音的时滞系统状态向量xTD∈RnTD×1。对于n层结构集中质量模型,结构系统的状态向量xS由相对于地面的位移qi和相对于地面的速度q·i组成,qi和q·i表示第i层的相对位移和相对速度,i=1,…n。
xS(t)=[q1[k],q·i[k],q2[k],…qn[k],q·n[k]]T.(2)
式中,开环系统矩阵A∈RnOL×nOL,B1∈RnOL×nw和B2∈RnOL×nu分别表示状态转移矩阵,激励影响矩阵和控制影响矩阵。向量z∈Rnz×1表示系统反应输出向量,也是反馈控制的目标,向量y∈Rny×1表示带有传感器噪音干扰的开环时滞系统的测量输出向量。相应地C1,D11和D12为目标输出矩阵,C2和D21为测量输出矩阵。考虑控制器计算的时间和数据传输时间的影响,传感器测量的信号假定延迟一个采样时间。
动态反馈控制器可根据开环测量输出y[k]作为控制力的输入信号来设计控制器出力的大小u[k],其状态方程为
{xG[k+1]=AGxG[k]+BGy[k],
u[k]=CGxG[k]+DGy[k].(3)
其中,xG为控制系统的状态向量; AG,BG,CG,DG为需要设计的控制器参数。
2 离散时域中的分散H∞控制器设计
2.1 分散控制器针对分散控制器,反馈信号y[k]和控制力u[k]可被分散为N组, 如:
y=[y1 … yi … yN]T,
u=[u1 … ui … uN]T.(4)
分组后的反馈信号与控制力分别组成多个子系统,从而系统式(3)被分为了N个子控制器系统,表示为
{xGi[k+1]=AGixGi[k]+BGiy[k],
ui[k]=CGixGi[k]+DGiyi[k].(5)
其中,AGi,BGi,CGi,DGi为第i个子控制系统。这样控制矩阵参数AG,BG,CG,DG便具有块对角的形式:
AG=diag(AGI,AGII,…,AGN),
BG=diag(BGI,BGII,…,BGN),
CG=diag(CGI,CGII,…,CGN),
DG=diag(DGI,DGII,…,DGN).(6)
这里假设式(1)中的D22为零矩阵(Gahinet,Apkarian,1994),令动态控制器维数与结构系统维数相同,即AG∈RnG×nG,nG=nOL。将式(3)代入到式(1)中,得到闭环系统:
{xCL[k+1]=ACLxCL[k]+BCLw[k],
z[k]=CCLxCL[k]+DCLw[k].(7)
其中,
ACL=A~+B~2G C~2,BCL=B~1+B~2G D~21,
CCL=C~1+D~12G C~2,DCL=D~11+D~12G D~21.(8)
式中:
[
A~ B~1 B~2C~1 D~11 D~12C~2 D~21 G
]=[
A 0 B1 0 B20 0nG 0 InG 0C1 0 D11 0 D120 InG 0 AG GGC2 0 D21 CG DG
].(9)
根据有界实引理,若H∞控制器存在并使得闭环系统式(7)稳定,系统的H∞范数小于给定的γ值,当且仅当存在一个正定对称矩阵P使得以下矩阵不等式成立:
[-P PACL PBCL 0
* -P 0 CTCL
* * -γI DTCL
* * * -γI]<0.(10)
将式(9)代入到式(10)当中,可得到矩阵不等式:
[-P P(A~+B~2G C~2 P(B~1+B~2G D~21)0
* -P 0(C~1+D~12G C~2)T
* * -γI(D~11+D~12G D~21)T
* * * -γI](11)
式中,存在矩阵变量P和G相乘的形式,若控制器矩阵AG,BG,CG,DG没有块对角结构形式限定时,通过投影引理(Gahinet,Apkarian,1994)可以将此矩阵相乘形式的BMI转化为多个LMI来进行求解。然而,分散控制器的矩阵是具有块对角形式的,难以等价转换为LMI,因此是非凸优化问题,难以求解。
2.2 双同伦法为解决双线性优化问题,Mehendale 和 Grigoriadis(2008)提出了双同伦的方法在连续时域中求解H∞分散控制器。本文基于双同伦法的思想,在离散时域中提出的H∞分散控制器求解方法。
在迭代过程开始时,即第0步(k=0),设初始变量G和P为集中控制器设计得到的矩阵GC和相对应的矩阵PC:
G0=GC=GC,diag+GC,off,
P0=PC.(12)
其中,矩阵GC,diag是由集中控制器设计得到的矩阵GC中对角块位置所对应的元素组成的; GC,off表示GC中剔除了矩阵GC,diag包含的元素后所剩余的矩阵,满足式(13)。当第k步时(k=1,2,…,K),Gk和Pk有如下形式:
λ=1/K,
Gk=Gk-1-λGC,off+ΔGk,
Pk=Pk-1+ΔPl.(13)
其中,K是总的迭代步数; 增量ΔGk与GC,diag结构形式相同; 增量ΔPk同Pk一样是对称的。随着k逐渐增大到K步,控制器矩阵Gk中非对角块元素逐渐变为0,对角块元素通过增量ΔGk逐渐地改变。当ΔGk和ΔPk足够小时,两者之间的乘积可以忽略不计,因此,式(11)可以被近似线性化为
Pk(A~+B~2GkC~2)≈Pk-1A^-+Pk-1B~2ΔGkC~2+ΔPkA^-
Pk(B~1+B~2GkD~21)≈Pk-1B^-+Pk-1B~2ΔGkD~21+ΔPkB^-.(14)
这样,式(11)不再有ΔGk和ΔPk相乘的形式,从而BMI约束被近似为LMI约束。式(13)二式代入到式(8)可得:
C~1+D~12GkC~2=C^-+D~12ΔGkC~2,
D~11+D~12GkD~21=D^-+D~12ΔGkD~21.(15)
其中,
A^-=A~+B~2(Gk-1-λGC,off)C~2,
B^-=B~1+B~2(Gk-1-λGC,off)D~21,
C^-=C~1+D~12(Gk-1-λGC,off)C~2,
D^-=D~11+D~12(Gk-1-λGC,off)D~21.(16)
最后可得到线性化的式(11)<0,定义是以ΔGk和ΔPk为变量的函数V(ΔGk,ΔPk)如下:
V(ΔGk,ΔPk)=[Pk-1+ΔPk Pk-1A^-+Pk-1B~2ΔGkC~2+ΔPkA^-
* Pk-1+ΔPk
* 0
* *
Pk-1B^-+Pk-1B~2ΔGkD~21+ΔPkB^- 0
0(C^-+D~12ΔGkC~2)T
-γI(D^-+D~12ΔGkD~21)T
* -γI]<0.(17)
通过以上可知BMI约束优化问题近似为了LMI约束优化问题,通过求解带有式(17)的约束优化问题便可得到理想分散控制器。
3 数值算例
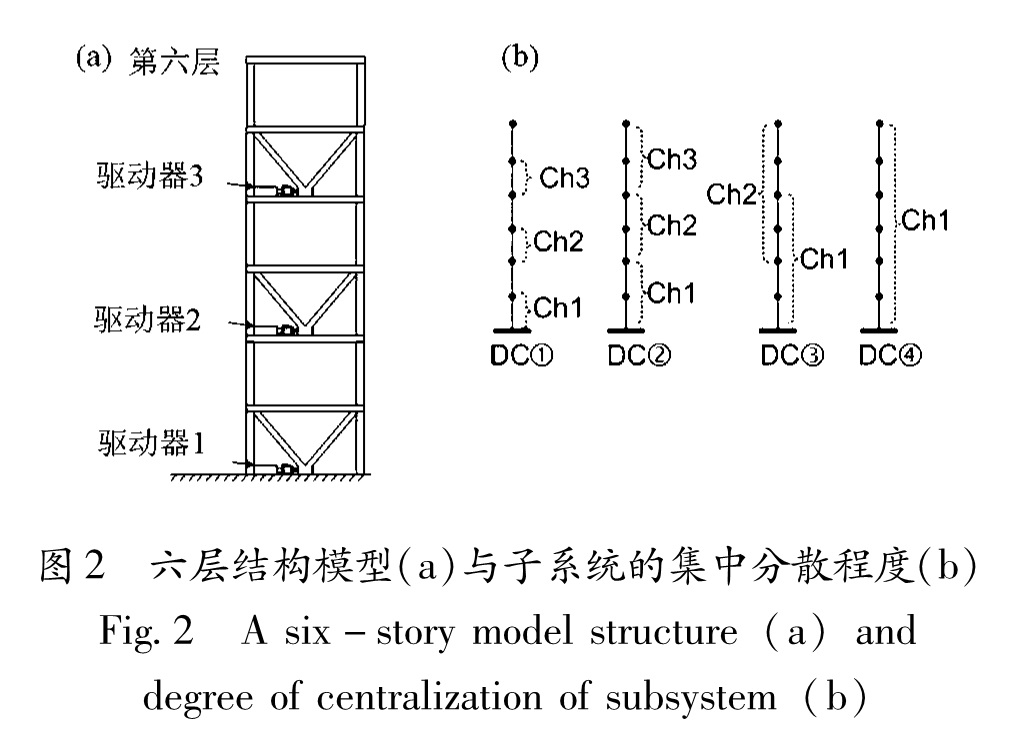
为了说明本文提出的分散控制器设计方法的有效性,对一个六层框架进行数值模,其结构如图2a
Fig.2 A six-story model structure(a)anddegree of centralization of subsystem(b)
所示,结构参数可参考Lu等(2008)所设定的。结构的1层、3层和5层分别安装了一个驱动器,给相邻两层提供控制力。
这里的测量输出m[k]为结构的层间位移,如式(18a)。反应输出z[k]为加权后的层间位移与控制力的组合,如式(18b)。
m[k]=[q1[k],q2[k]-q1[k],…,q6[k]-q5[k]]T(18a)
z[k]=[(104)1/2(q1[k],q2[k]-q1[k],…,q6[k]-q5[k]),(10-9)1/2(u1,u2,u3)]T.(18b)
图2b描述了子系统的集中和分散程度,用DC表示(degrees of centralization,DC)。
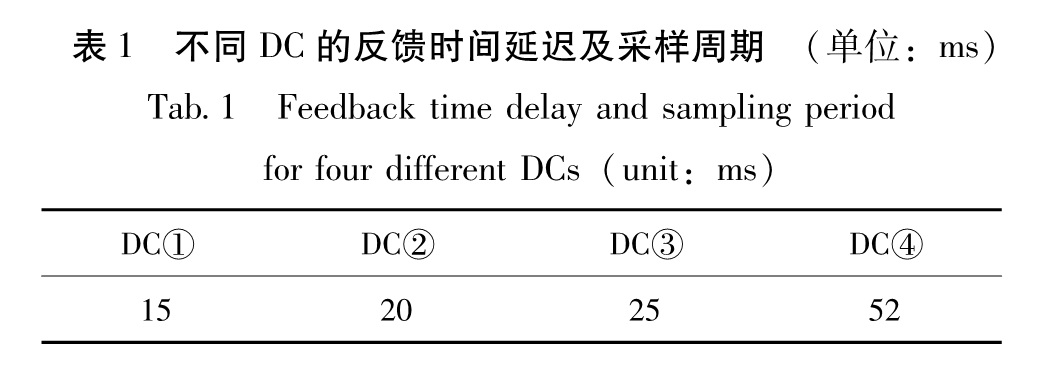
假设延迟时间等于一个采样周期。根据传感器传输信息多少与距离长短,可定义延迟时间如表 1所示。
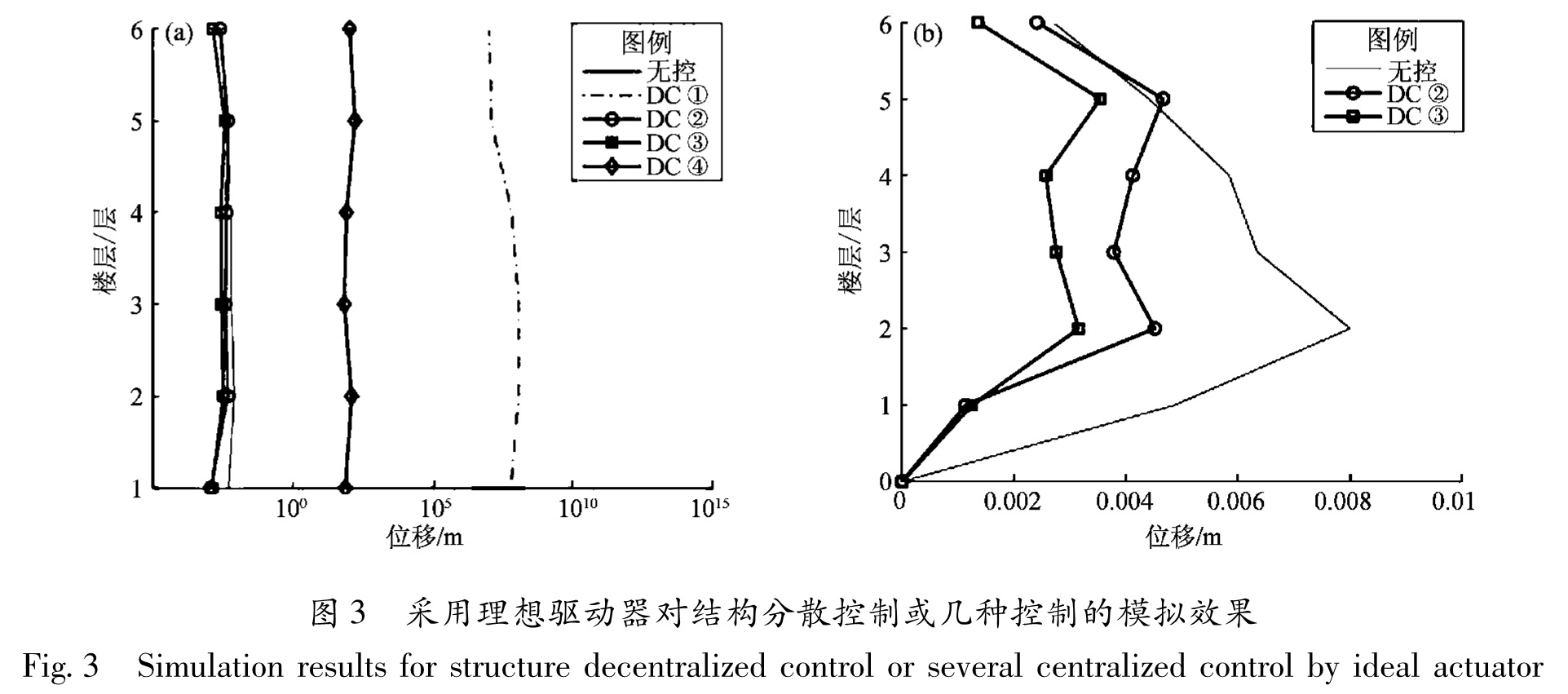
Tab.1 Feedback time delay and sampling period for four different DCs(unit:ms)地震激励采用1940年的El Centro NS地震记录。加速度峰值调整为1 m·s-2。通过计算得到层间唯一峰值,并做比较。图3a为结构层间位移最大值的对比,从图中看到,DC①和DC②呈现了不稳定的结构反应,这是由于积分过程中出现了数值不稳定的情况,正是由于时滞大导致的。
为进一步说明分散控制方法的效果,需对稳定的情况进行对比,即DC②、DC③和无控状态,如图3b所示。在无控状态下,第二层的层间位移峰值达到最大。DC②、DC③可明显减小结构的层间位移的最大峰值。另外发现,DC③的减振效果由于DC②的作用,这是因为时滞都不长的情况下,反馈信息多有助于减振控制。
4 结论
本文考虑大尺度结构反馈控制中的时滞问题,在离散时域中提出了基于双同伦的方法分散H∞控
Fig.3 Simulation results for structure decentralized control or several centralized control by ideal actuator制器的求解方法。该方法将双线性矩阵不等式近似化为线性矩阵不等式,通过迭代搜索求解控制器。从而解决了矩阵不等式非凸优化问题求解过程中带有特殊结构形式的矩阵的问题。并通过六层数值算例进行了验证,结果表明在延迟时间不大时,反馈的信息越多,控制效果越好; 而延迟过大或信息过少都会导致控制性能变差的情况。
- Gahinet P,Apkarian P.1994.A linear matrix inequality approach to H∞ control[J].International Journal of Robust and Nonlinear Control,4(4):421-448.
- Kocvara M,Stingl M.2003.PENNON-A Code for Convex Nonlinear and Semidenite Programming[J].Optimization Methods and Software,18(3):317-333.
- Loh C H,Chang C M.2008.Application of centralized and decentralized control to building structure:analytical study[J].Journal of Engineering Mechanics,134(11):970-982.
- Lu K C,Loh C H,Yang J N,et al.2008.Decentralized sliding mode control of a building using MR dampers[J].Smart Materials and Structures,17(5):055006.
- Lynch J P,Law K H.2002.Decentralized control techniques for large scale civil structural systems[C]//Proceedings of the 20th International Modal Analysis Conference.Los Angeles,CA.
- Ma T W,Xu N S,Tang Y.2008.Decentralized robust control of building structures under seismic excitations[J].Earthquake Engineering & Structural Dynamics,37(1):121-140.
- Mehendale C S,Grigoriadis K M.2008.A double homotopy method for decentralised control design[J].International Journal of Control,81(10):1600 -1608.
- Rofooei F R,Monajemi-Nezhad S.2006.Decentralized control of tall buildings[J].The Structural Design of Tall and Special Buildings,15(2):153-170.
- Sandell N,Varaiya J P,Athans M,et al.1978.Survey of decentralized control methods for large scale systems[J].Automatic Control,IEEE Transactions on,23(2):108-128.
- Siljak D D.1991.Decentralized Control of Complex Systems[M]//Mathematics in science and engineering.Boston:Academic Press.
- Siljak D D.1996.Decentralized control and computations:status and prospects[J].Annual Reviews in Control,20(2):131-141.
- Swartz R A,Lynch J P.2006.Redundant Kalman Estimation for a Distributed Wireless Structural Control System[C]//Proceedings of the US-Korea Workshop on Smart Structures Technology for Steel Structures.Seoul,Korea.
- VanAntwerp J G,Braatz R D.2000.A tutorial on linear and bilinear matrix inequalities[J].Journal of Process Control,10(4):363-385.
- Wang Y,Law K H,Lall S.2009.Time-delayed decentralized H∞ controller design for civil structures:a homotopy method through linear matrix inequalities[C]//Proceedings of the 2009 American Control Conference(ACC 2009).St.Louis,MO,USA.
- Wang Y,Swartz R A,Lynch J P.et al.2007.Decentralized civil structural control using real-time wireless sensing and embedded computing[J].Smart Structures and Systems,3(3):321-340.
- Wang Y.2011.Time-delayed dynamic output feedback H∞ controller design for civil structures:a decentralized approach through homotopic transformation[J].Structural Control and Health Monitoring,18(2):121-139.
- Xu B,Wu Z S,Yokoyama K.2003.Neural networks for decentralized control of cable-stayed bridge[J].Journal of Bridge Engineering,8(4):229-236.