基金项目:国家自然科学青年基金(41104027)、浙江省自然科学基金重点项目(LZ14D060001)和海洋科学浙江省重中之重学科开放课题(20130113)联合资助.
(浙江海洋大学 海洋科学与技术学院,浙江 舟山 316022)
(School of Marine Science and Technology,Zhejiang Ocean University, Zhoushan 316022, Zhejiang, China)
Hilbert-Huang transform; air-gun source; high-frequency pressure pulse; low-frequency bubble pulse
备注
基金项目:国家自然科学青年基金(41104027)、浙江省自然科学基金重点项目(LZ14D060001)和海洋科学浙江省重中之重学科开放课题(20130113)联合资助.
通过Hilbert-Huang变换对浅水环境下气枪震源激发子波特征进行了研究,结果表明:气枪震源首先激发高频压力脉冲,其频带相对较宽,优势频率为40~80 Hz,主频随时间降低; 随后高压气体在水下形成的气泡振荡激发低频气泡脉动,其频带相对较窄,优势频率为4~12 Hz,且水深较浅处的气泡振荡激发的气泡脉动主频相对较低。研究结果有助于提高对浅水环境下气枪震源激发的复杂近场信号的认识。
The characteristics of wavelet excited by the air-gun source in shallow water was studied by using the Hilbert-Huang transform. The results indicate that: firstly, the high frequency pressure signal which was excited by the air-gun of pressure pulse has the characteristic of broad frequency band,and dominant frequency with 40~80 Hz, and the primary frequency decreases with time. Then the low frequency bubble pulse which was excited by bubble oscillation induced by high pressure gas in underwater had the characteristic of narrow frequency band,the dominant frequency with 4~12 Hz, and the main frequency of bubble pulse excited by the bubble oscillation was relatively low in shallower water. The obtained study results will contribute to understanding the complicated near-field air-gun signal in shallow water.
引言
地震波是唯一能够穿透地球内部的振动,迄今为止,关于地球内部的结构、组成、过程和状态的研究等多来自地震波的信息(陈颙,朱日祥,2005)。震源是产生地震波的源头,其所产生的地震波信号的品质将直接影响地震探测的效果。气枪震源自1964年由美国Bolt公司的卡尔米思克发明以来,逐渐被发展成为具有绿色环保、可重复性好、可控性强、子波可测等卓越性能的水中震源,而被广泛应用于海洋地震勘探(其中以地下油气、矿藏等资源的局部尺度探测为主)(Calvert,2004)。近年来,气枪震源也逐渐被应用于区域尺度的地震探测,出现了利用海洋激发气枪、陆地接收信号的科学尝试,如美国的LARSE(Los Angeles Region Seismic Experiment)计划(Lutter et al, 1999; Fuis et al, 2003)、新西兰的SIGHT(South Island Geophysical Transect)计划(Okaya et al, 2002; Stern et al, 2002; Avendonk et al, 2004)以及国内的南海北部海陆联测试验(赵明辉等,2004; 丘学林等,2007)。由于水中炸药爆破存在可控性差、激发可重复性低以及作业费用高等缺点,气枪震源亦开始逐渐成为陆地水域激发地震波的选择。国内在陆上水库进行的气枪震源激发实验表明:大容量气枪震源是一种优良的水中震源,具有激发能量大、地震波转换率高、传播距离远等特点,是陆上激发地震波的一种新方法(陈颙等,2007a,b; Chen et al, 2008; 林建民等,2008a,b; 杨微等,2013; 刘自凤等,2015; 苏金波等,2015; 王彬等,2015)。
通过大量的理论研究与实验观测,人们已经很好地掌握了深海气枪源的震源特性和以此组建气枪阵列的技术(Mayn,Quay, 1971; Caldewll, Dragoset, 2000; Dragoset, 2000; 罗桂纯等,2007)。深海中气枪作业水深多在30 m以上,如LARSE 计划中气枪的沉放水深大于100 m(Fuis et al,2003),周围水体较大,震源相对比较独立,激发信号受水底、水面反射等影响较小,激发过程相对比较简单,这使得震源特性几乎完全由气枪本身决定。但水深较浅的陆地水域水体相对较小,使用气枪震源必须综合考虑气枪震源与水域的相互作用、耦合等诸多问题,其激发地震波受激发条件和激发环境多种因素(水深、沉放深度、水底地形、边界及沉积等)的影响,因此,其激发特性与规律和深海气枪源存在很大差异。尽管水库气枪激发作为陆地震源的有效性已经得到验证(陈颙等,2007b),但至今针对浅水环境下气枪震源激发特性及激发地震波规律的研究甚少。林建民等(2010)曾重点分析了沉放深度、工作压力等参数对水库气枪震源激发波形的影响,但尚未从气枪震源信号本身特征出发加以分析。
气枪震源信号是典型的非线性、非平稳信号,即统计量(相关函数、功率谱等)随时间而变化。Huang等(1998)提出了一种分析非平稳非线性时间序列的新方法,即Hilbert-Huang变换(Hilbert-Huang Transform, 简称HHT)。该方法通过经验模态分解(Empirical Mode Decomposition, 简称EMD),根据信号本身的时间尺度特征,将信号分解为有限个可以视为窄带信号的本征模态函数(Intrinsic Mode Function, 简称IMF),并通过各IMF的Hilbert变换获得具有明确定义和物理意义的瞬时频率,建立了以本征模态函数为基本时域信号、以瞬时频率作为基本量表征信号变化的新时频分析方法。本文将利用HHT方法研究水库气枪震源激发信号时频特征,并获得瞬时频率等瞬时地震属性,提高对浅水环境下气枪震源激发的复杂近场信号的认识。
1 Hilbert-Huang变换
Hilbert-Huang变换的基本思想是将待考察时间序列通过经验模态分解获得若干个IMF,然后利用Hilbert变换对每一个IMF构造相应的解析信号,通过其模和幅角的时间导数获得瞬时振幅和瞬时频率,构成Hilbert谱,获得原始时间序列不同时间尺度的振荡特征。Hilbert-Huang变换主要由经验模态分解和Hilbert谱分析2部分构成(Huang et al, 1998; Rilling, Flandrin, 2008)。
1.1 经验模态分解经验模态分解的关键是将一个非线性非平稳时间序列分解为有限个IMF分量和一个趋势项。由于每个时间序列都是由多个时间尺度的振荡波构成,因此,该方法从本质上是将一个信号序列进行平稳化的过程,其处理过程是将信号中的这些固有的、内在的波动或趋势项按照不同的时间尺度逐级分解开来,产生一系列具有不同时间尺度的IMF。
该方法可通过包络线方法进行逐级筛选,实现时间序列的经验模态分解,求出全部有限个IMF,主要步骤包括:
(1)对于原始序列X(t)的局部极大值和极小值,用三次样条函数插值形成极大值包络Xmax(t)和极小值包络Xmin(t);
(2)求取极大值包络与极小值包络的瞬时均值线
m1(t)=1/2[Xmax(t)+Xmin(t)].(1)
(3)考察原始序列X(t)与瞬时均值m1(t)差值,即去掉低频的新序列h1(t)=X(t)-m1(t),判定其是否满足以下IMF要求,如果满足,则将h1(t)作为第一个IMF分量C1; 如果不满足,则将h1(t)作为原始序列重复以上筛选过程,依次筛选,直至第k次筛选结果符合要求,即得到第一个IMF分量C1。
这样得到的C1应是时间序列中特征时间尺度最小的高频IMF分量。然后将C1从原序列 X(t)中分离出去,得到一个剩余序列r1=X(t)-C1,由于r1中可能含有比 C1的特征时间尺度大的IMF,因此又将r1作为新的序列实施上述(1)~(3)筛选过程,以求得第二个IMF分量C2。如此重复,求出一系列IMF,直至剩余序列rn(趋势项)成为一个单调函数,从中再也不能分解出IMF分量时,整个分解过程结束。此时,原始序列可表示成为n个IMF和1个趋势项之和,即
X(t)=∑nj=1Cj(t)+rn(t).(2)
其中,IMF分量Cj需满足以下条件:
(1)在整个资料集里,极值点的数目和穿零点的数目必须相等或者最多相差1个;
(2)由局部极大值所构成的包络线和由局部极小值所构成的包络线的平均值为零。
从上述EMD过程可以看出,该方法的优点在于:直观、直接、基于数据本身特征以及自适应性强。
1.2 Hilbert谱分析与瞬时属性对于任一时间序列X(t),其Hilbert变换Y(t)定义为
Y(t)=1/nP+∞-∞(X(τ))/(t-τ)dτ.(3)
其中,P表示Cauchy主值。数学上,式(3)表示X(t)与1/t的卷积,因此,Hilbert变换强调X(t)的局部性。在1/t的基础上,构造解析信号Z(t)为
Z(t)=X(t)+iY(t)=a(t)eiθ(t).(4)
式中,a(t)为瞬时振幅,θ(t)为瞬时相位,对其求导可得瞬时频率ω(t)为
ω(t)=(dθ(t))/(dt).(5)
为使瞬时频率ω(t)具有实际意义,信号X(t)必须为窄带信号,其函数图像关于零均值线是局部对称的,并且穿零点和极值的数目是一样的。若以上条件不满足,所求出的瞬时频率就可能出现异常值或负数。
通过EMD所分解得到的IMF为窄带信号,符合作Hilbert变换求取瞬时频率的要求,因此,原始信号可以用其各个IMF分量的瞬时频率ωj(t)和瞬时振幅aj(t)近似地表示成
H(ω,t)=RE[∑nj=1aj(t)eiωj(t)dt].(6)
式(6)即为Hilbert谱,其中,RE表示求取实部运算。ωj(t)和 aj(t)都随时间而变化,体现了非平稳序列的本质特征,突破了传统傅立叶分析中定常振幅和固定频率的限制。Hilbert谱将信号的振幅表示成为瞬时频率和时间的函数,描述了其在整个频率域上随时间和频率的变化规律。
2 气枪震源信号时频特征及瞬时属性
本文所研究信号为容量2 000 in3气枪震源(Bolt 1500LL型)在水深18 m的陆上水库环境下的激发信号,气枪沉放深度10 m,工作压力(气枪中压缩气体的压力)10 MPa,距离气枪激发点水平距离50 m、深8 m位置处布设水听器(采样率200 Hz,频带50 Hz~40 kHz)所记录的近场子波信号(林建民等,2010)。海洋石油勘探通常采用气枪阵列作为震源,其子波测量点与气枪源之间的距离通常在几百米以上,主要是为了使阵列中各单枪激发信号能同时(在一个采样时间间隔内)到达水听器,而本文工作中采用单枪激发,且重点研究近场信号特征。
图1为气枪激发信号的原始波形及其EMD结果,图1a是水听器记录的实际波形,图1b是分解得到的7个本征模态函数(IMF1~IMF7),其中IMF7是剩余项。观察各IMF分量时域波形,不同IMF分量包含了不同的时间特征尺度,分别以不同的分辨率显示了气枪信号特征,并且这种分辨率是自适应的。IMF1~IMF7分别是从高频至低频分量逐级分解获得,其中,IMF1和IMF2主要对应气枪震源信号的高频压力脉冲,平稳性相对较差; 而IMF3和IMF4主要对应后续的低频气泡脉冲,平稳性比较好。
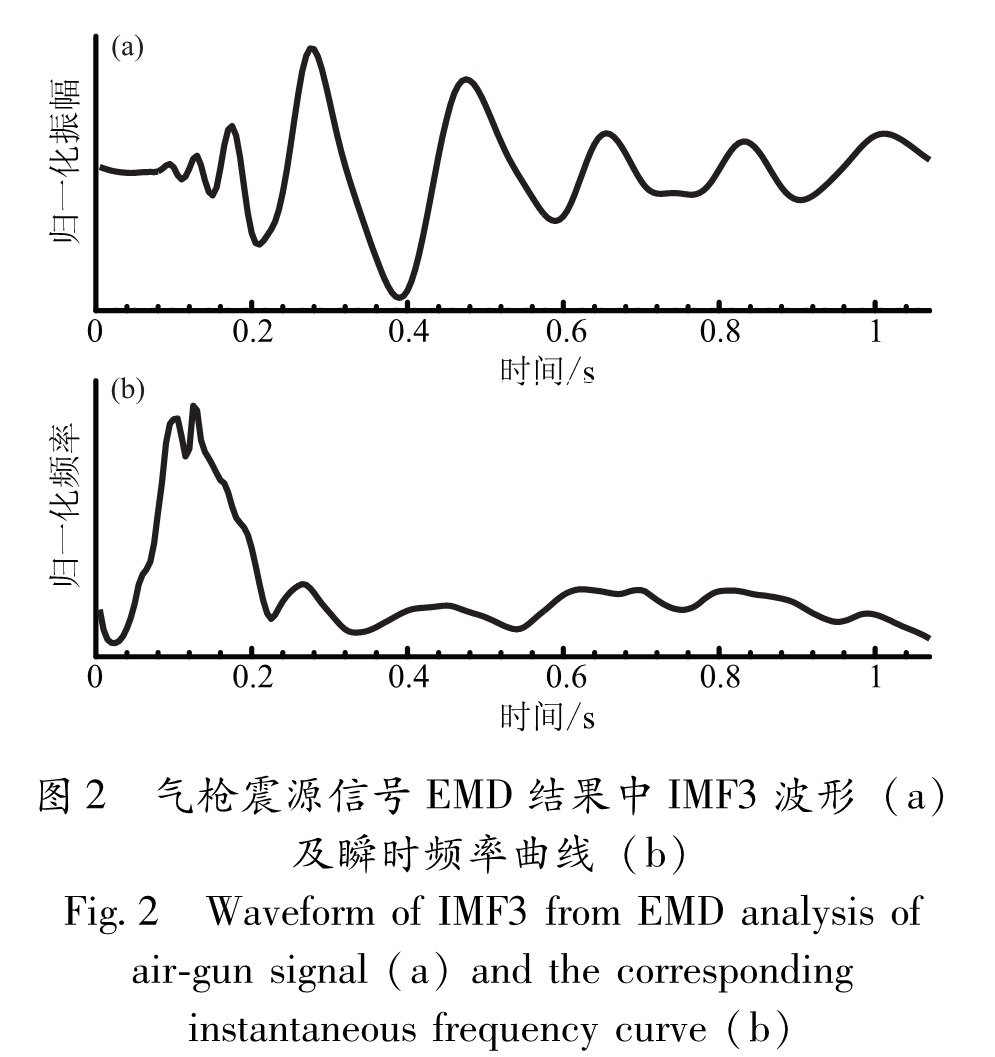
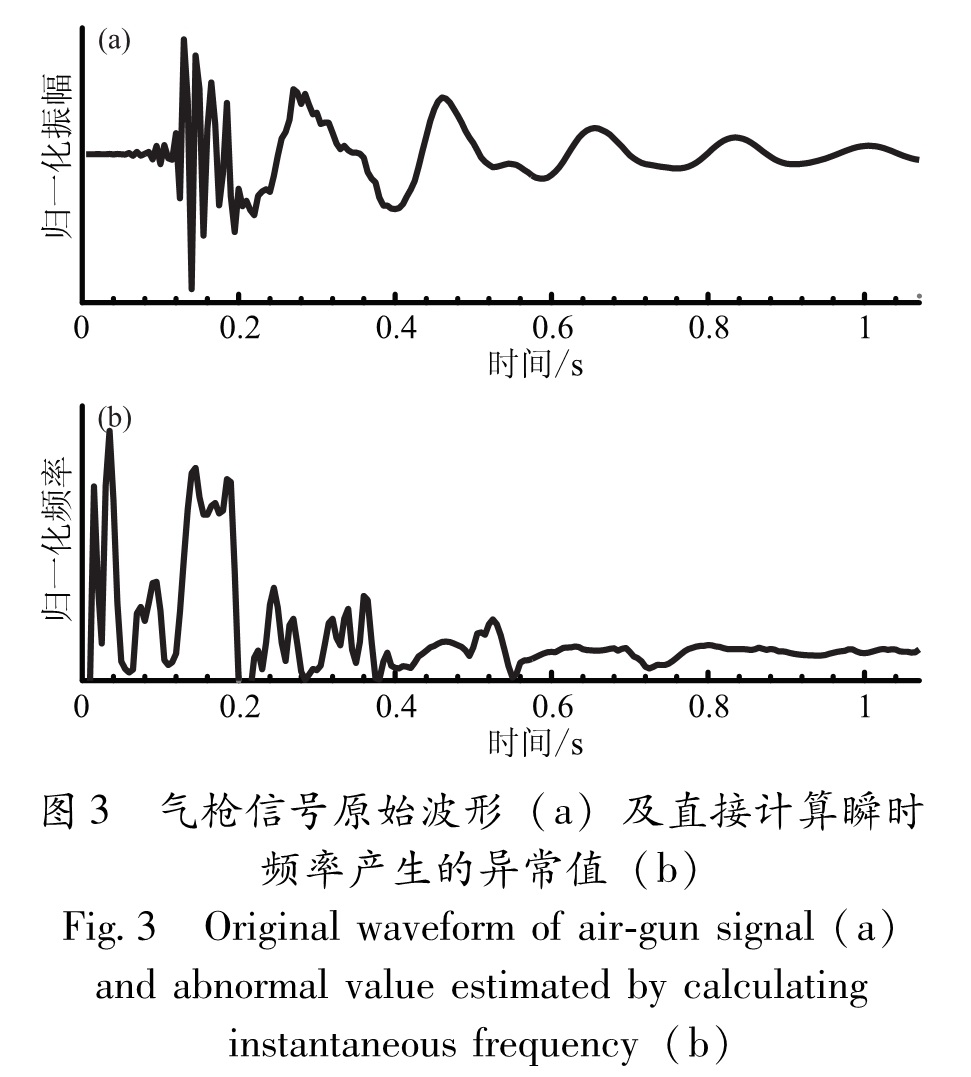
在地震探测中,瞬时属性(主要指瞬时振幅、瞬时相位和瞬时频率)不仅可以用来研究地球介质的构造、岩性等,还可以反演介质的品质因子等(Matheney, Nowack, 1995)。瞬时属性通常利用Hilbert变换构造相应复信号后进行求取,但该方法在信号是窄带或平稳的情况下所求取的瞬时属性才有物理意义,因此,对于非线性、非平稳的气枪信号无法直接通过此方法求瞬时属性。EMD获得的IMF1~IMF7虽然是从高频至低频逐级分解的结果,但并不是简单地在频率域进行带通滤波,其本质是将信号进行平稳化的过程,将信号中固有的、内在的波动成分按照不同的时间尺度逐级分解,使分解得到的IMF具有窄带特性,以符合利用Hilbert变换求取具有实际物理意义瞬时属性的要求。图2为气枪信号EMD结果中IMF3的瞬时频率计算结果,即频率随时间的变化曲线。若直接利用原始波形进行Hilbert变换求瞬时频率,则因其不完全满足Hilbert变换的前提假设条件而产生异常值,不利于真正利用瞬时频率掌握源信号频率的时间变化,如图3所示。由图2可知,尽管IMF3的主要频率范围对应低频气泡脉冲,但是在高频压力脉冲位置仍有部分微小能量分布,导致在瞬时频率曲线上出现高频成分分布,这也说明不同IMF之间有频率交叉,并不是上述的简单频域带通滤波。图2 气枪震源信号EMD结果中IMF3波形(a)
及瞬时频率曲线(b)
Fig.2 Waveform of IMF3 from EMD analysis of air-gun signal(a)and the corresponding instantaneousfrequency curve(b)气枪震源激发信号分高频压力脉冲和低频气泡脉冲,前者为高压气体瞬间释放到水中激发压力波,因具有较高频率通常用于浅层石油勘探,后者为高压气体释放到水中之后形成后续气泡振荡所产生,主频相对较低,适合长炮检距的深部结构探测。从图2可以看出,IMF3在0.2 s附近瞬时频率迅速由高频转为低频,对应压力脉冲向气泡脉冲过渡,即高压气体瞬间释放到水中激发压力波之后形成的气泡在0.2 s附近开始振荡。但为掌握气枪震源信号整体频率随时间的变化规律以及信号振幅或能量随频率和时间的变化分布情况,则需通过Hilbert变换的谱分析获得Hilbert时频谱,将振幅表示成为瞬时频率和时间的函数。图4给出了本文所分析气枪信号的波形、功率谱密度分析及相应的Hilbert时频谱,能清晰地刻画出气枪信号的时频特征。由于Hilbert时频谱包含了详细的IMF分量频率变化的信息,能准确反应信号的时频特性,可以清晰地分辨出信号主频的突变及所对应的时刻,因此,具有更高的时间—频率域分辨率。
3 不同时频分析方法讨论
目前,用于分析地震信号的最常用的、且较为成熟的方法是傅立叶变换。但由于傅立叶变换严格要求系统的线性、数据的周期性或平稳性(即傅立叶频率代表着信号的周期性),在处理非平稳、非线性数据时,其实际应用受到很大的限制。如本文中气枪信号为非平稳信号,其特点之一就是无周期性,若按傅立叶变换方法定义其频率进行频谱分析将缺乏物理基础。因此,引入具有真实物理意义的瞬时频率ω(t)对于研究气枪信号瞬态特性具有重要的意义。
通常可利用Hilbert变换求取信号具有实际物理意义的瞬时属性,但要求被分析信号是窄带或平稳的,而且该方法对噪声很敏感。而气枪震源信号等实际地震信号既非平稳又含有噪声,直接对其进行Hilbert变换求取瞬时频率等属性参数,将缺乏物理意义甚至失真(图3)。HHT的根本创新就在于先通过EMD将信号进行平稳化,将信号中固有的、内在的波动成分按照不同的时间尺度逐级分解成窄带信号分量IMF,使其满足利用Hilbert变换求取具有实际物理意义瞬时属性的要求,再分别计算每个分量对应的瞬时频率等瞬时属性。瞬时频率作为时间的函数,能敏锐地识别出待分析信号中的多尺度嵌套结构(图2)。
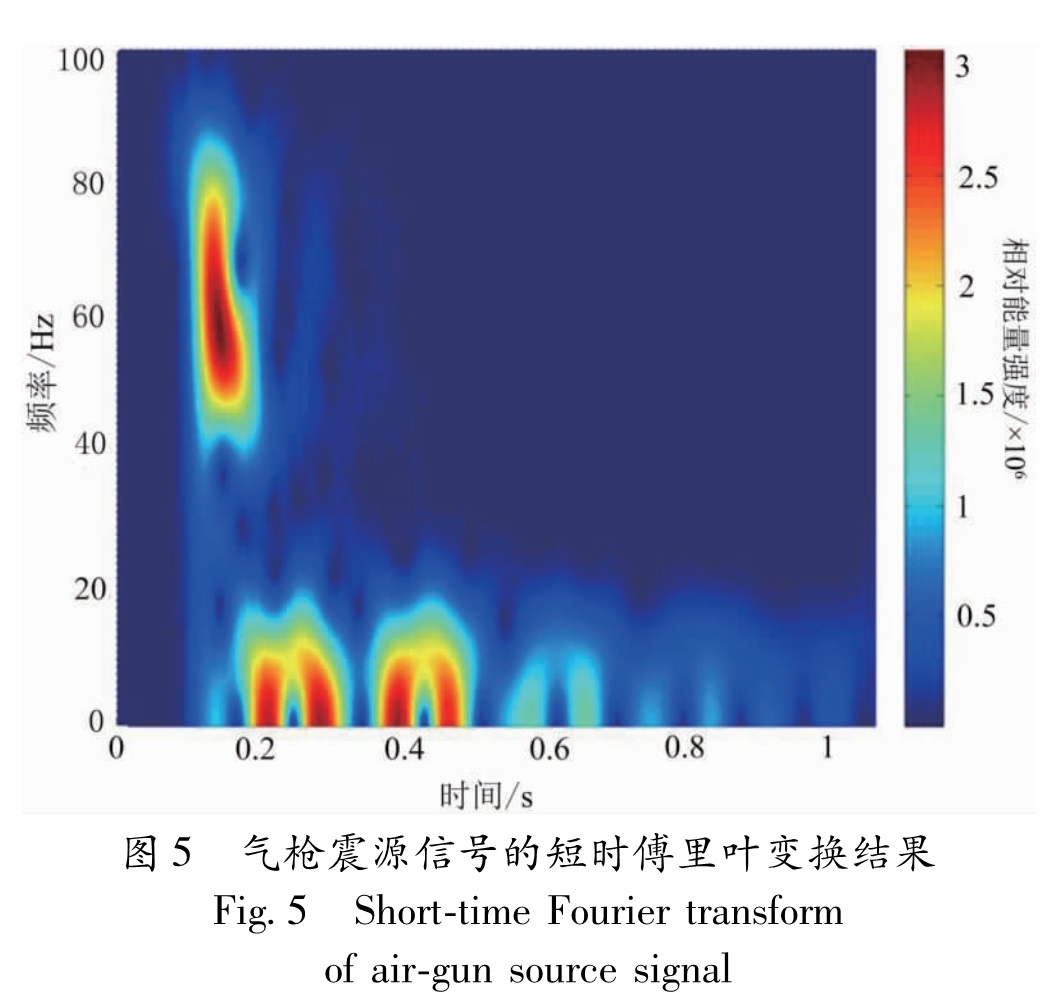
傅立叶变换是一种纯频域分析方法,是将信号从时域转换到频域的整体变换,无法提供时域信息。若要获得某一时刻的频率特性,则通常采用时频分析方法,这也是针对非平稳信号较为常用的处理方法,比较典型的有短时傅立叶变换、小波变换等(李春峰,Linea, 2005; 陈雨红等,2006)。但这些方法基本上都是将信号序列在某种基底函数系上展开,然后分析展开系数及各分量的特征。如短时傅立叶变换实际上是加窗傅立叶变换,通常假设信号在窗函数的有效持续时间内是平稳的,但此条件通常无法满足或只是近似满足,因而它的时间和频率分辨率都很低。图5为所分析的气枪震源信号通过短时傅立叶变换所获得的时频特征。小波分析虽然通过一系列可伸缩平移的小波函数实现了信号时频局部化分析目的,但在本质上仍然是具有柔性时频窗的加窗傅立叶变换(崔锦泰,2006),它也要求小波窗内的信号是短时平稳的,还没有根本摆脱傅立叶变换的局限性。而且,小波基选择的多样性和使用过程中的不可变更性也影响了它在非平稳信号分析中的适应能力。同时,小波基的有限长会造成信号的能量泄漏,因而难以对信号作精确的时频分析。
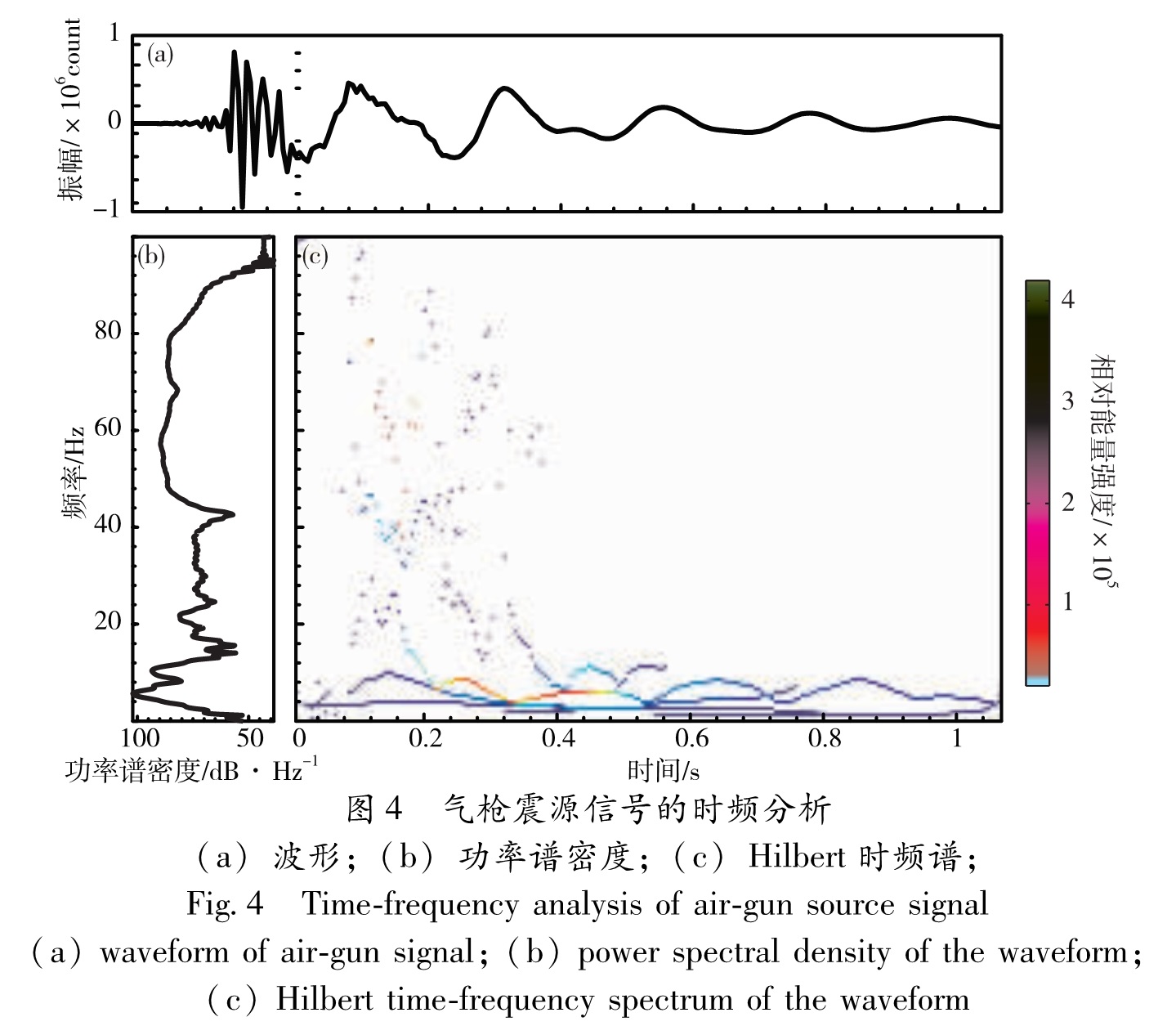
图4 气枪震源信号的时频分析
(a)波形;(b)功率谱密度;(c)Hilbert时频谱;
Fig.4 Time-frequency analysis of air-gun source signal(a)waveform of air-gun signal;(b)powerspectral density of the waveform; (c)Hilbert time-frequency spectrum of the waveformHHT与传统时频分析方法最大的不同就是不采用固定的基底分解,而是基于信号本身的局部特征时间尺度进行分解获得IMF分量,大大提高了其自适应性,有效克服了傅立叶变换中测不准原理的限制,在客观性和分辨率方面具有明显的优势,更适用于非平稳、非线性信号处理。该方法能用分解得到的IMF分量及1个剩余项来揭示信号序列的振荡结构特征和非平稳性,并最终由每个IMF分量经过Hilbert变换得到时域和频域均具有较高分辨率的Hilbert谱(图4c),具有明确的物理意义,且可以准确给出原信号序列及其IMF分量的主要振幅变化所对应的频率和时间,即反映物理过程能量—频率—时间的分布。
由于Hilbert时频谱是通过计算IMF分量的瞬时频率和瞬时幅度而直接得到,因此,其时间和频率分辨率不同于其他时频分析方法受Heisenberg不确定原理的限制,而是相互独立的。相比于图5所示基于短时傅里叶变换所得的时频特征,图4c所示的Hilbert时频谱具有更好的局部时频特性表现能力,从图中可以观察到气枪信号能量随时间和频率的精细变化趋势。从0.12 s左右开始,高频压力脉冲激发,由于信号脉冲较陡,其频带覆盖范围较宽,优势频段则主要集中在40~80 Hz。同时,得益于Hilbert谱的高时频分辨率,还能观察到压力脉冲(图4c中0.12~0.18 s之间原始波形中的4个脉冲峰)中后面的脉冲比前面的脉冲主频低,即压力脉冲主频随时间递减,从80 Hz降低到40~60 Hz,然后直接过渡到后续的低频气泡脉冲。其原因可能是后面的脉冲是由压力脉冲在水面及水底的反射或压力脉冲本身的振荡产生,其主频在水介质中传播及两相界面上反射过程中下降或自身振荡过程中下降。从0.2 s附近开始,释放的高压气体在水下形成的气泡开始振荡激发低频气泡脉冲,持续时间达0.5 s以上,其优势频率集中在4~12 Hz的低频范围。从图4b的分析结果可得,低频气泡脉冲在6 Hz和10 Hz附近有2个尖峰,但缺少了时域的分辨信息。而从图4c中可以推测,10 Hz的尖峰能量可能主要来自于第一次气泡振荡,而6 Hz的尖峰能量主要来自于第二次气泡振荡。该实际计算结果与林建民等(2010)的分析结果中公式(1)相符合,由于气泡脉冲激发过程对应着逐渐上浮的水下气泡振荡过程,第二次气泡振荡水深位置相对于第一次气泡振荡更浅,因此,公式(1)中P00更小,且R0更大,导致气泡振荡周期T更大,即对应气泡脉冲主频更低,所以,后续的气泡脉冲主频要低于前面的气泡脉冲(图4)。此外,在0.12 s压力脉冲到达之前,存在微小振幅的振荡波形,这可能由采集过程中滤波因素引起,它对后续的Hilbert谱计算可能引入一定的干扰。本文对气枪震源信号的处理分析结果显示了HHT方法的有效性,但同时也注意到该方法在应用过程中对噪声的敏感性以及边界问题的影响,如图4中t=0附近出现近微小能量的近100 Hz高频能量,这个是由边界效应引起的干扰。如何进一步消除信号中夹杂噪声及边界效应的影响,对于进一步提高HHT的应用效果至关重要,这是该方法需要进一步完善的地方,也是在应用过程中需要进一步研究的问题。
4 结论
HHT是近年发展起来的处理非线性、非平稳信号的高效时频分析方法,该方法通过EMD将信号分解为IMF窄带分量,并计算其具有实际物理意义的瞬时频率,掌握信号频率的时间变化特征。在此基础上,进一步通过Hilbert谱分析获得在时域和频域均具较高分辨率的时频谱,更为清晰地表征信号的时频分布特征。气枪震源信号为典型的非平稳信号,若直接利用基于傅立叶变换的各种处理方法,所获得的频率信息物理意义不明确,时频分析结果分辨率不高。本文利用HHT对水库气枪震源近场信号实际水听器记录数据进行了分析,相对于以往工作,在气枪震源信号在不同时间尺度上振荡特征、具真实物理意义瞬时频率时间变化特征、时频域高分辨率能量分布特征及原因等方面获得了更多认识,有助于对浅水环境下气枪震源激发的复杂近场信号的理解。
感谢中国地震局地球物理研究所水库气枪试验及其他参与单位对本文工作的支持。
- 陈颙, 朱日祥. 2005. 设立“地下明灯研究计划”的建议[J]. 地球科学进展, 20(5): 485-489.
- 陈颙, 李宜靖. 2007a. 地震波雷达研究展望: 用人工震源探测大陆地壳结构[J]. 中国科学技术大学学报, 37(8): 813-819.
- 陈颙, 张先康, 丘学林等. 2007b. 陆地人工激发地震波的一种新方法[J]. 科学通报, 52(11): 1317-1321.
- 陈雨红, 杨长春, 曹齐放等. 2006. 几种时频分析方法比较[J]. 地球物理学进展, 21(4): 1180-1185.
- 崔锦泰. 2006. 小波分析导论[M]. 西安: 西安交通大学出版社.
- 李春峰, Liner C. 2005. 基于小波多尺度分析的奇性指数: 一种新地震属性[J]. 地球物理学报, 48(4): 882-888.
- 林建民, 王宝善, 葛洪魁等. 2008a. 大容量气枪震源特征及深部介质中传播的震相分析[J]. 地球物理学报, 51(1): 206-212.
- 林建民. 2008b. 基于人工震源的长偏移距地震信号检测和探测研究[D]. 合肥: 中国科学技术大学.
- 林建民, 王宝善, 葛洪魁等. 2010. 大容量气枪震源子波激发特性分析[J]. 地球物理学报, 53(2): 342-349.
- 刘自凤, 苏有锦, 王宝善等. 2015. 宾川主动源地震波走时变化分析方法研究[J]. 地震研究,38(4):591-597.
- 罗桂纯, 葛洪魁, 王宝善等. 2007. 气枪震源激发模式及应用[J]. 中国地震, 23(3): 225-232.
- 丘学林, 陈颙, 朱日祥等. 2007. 大容量气枪震源在海陆联测中的应用: 南海北部试验结果分析[J]. 科学通报, 52(1): 1-7.
- 苏金波, 王宝善, 王海涛等. 2015. 利用大容量气枪震源资料研究北天山地区介质衰减特征[J]. 地震研究,38(4): 598-605.
- 王彬, 吴国华, 苏有锦等. 2015. 宾川地震信号发射台的选址、建设及初步观测结果[J]. 地震研究,38(1): 1-6.
- 杨微, 王宝善, 葛洪魁等. 2013. 大容量气枪震源主动探测技术系统及试验研究[J]. 中国地震,29(4): 339-410.
- 赵明辉, 丘学林, 夏戡原等. 2004. 南海东北部海陆联测地震数据处理及初步结果[J]. 热带海洋学报, 23(1): 58-63.
- Avendonk H J A V, Holbrook W S, Okaya D, et al. 2004. Continental crust under compression: a seismic refraction study of South Island Geophysical Transect, South Island, New Zealand [J]. J Geophys Res, 109(B6): B06302.
- Caldewll J, Dragoset W. 2000. A brief overview of seismic air-gun arrays [J]. The Leading Edge, 19(8): 898-902.
- Calvert A J. 2004. Seismic reflection imaging of two megathrust share zones in the northern Cascadia subduction zone [J]. Nature, 428(6979): 163-167.
- Chen Y, Liu L, Ge H, et al. 2008. Using an airgun array in a land reservoir as the seismic source for seismotectonic studies in northern China: experiments and preliminary results [J]. Geophysical Prospecting, 56(4): 601-612.
- Dragoset B. 2000. Introduction to air guns and air-gun arrays [J]. The Leading Edge, 19(8): 892-897.
- Fuis G S, Clayton R W, Davis P M, et al. 2003. Fault systems of the 1971 San Fernando and 1994 Northridge earthquakes, southern California: Relocated aftershocks and seismic images from LARSE II [J]. Geology, 31(2): 171-174.
- Huang N E, Shen Z, Long S R, et al. 1998. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series and analysis [J]. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 454(1971): 903-995.
- Lutter W J, Fuis G S, Thurber C H, et al. 1999. Tomographic images of the upper crust from the Los Angeles basin to the Mojave Desert, California: Results from the Los Angeles Region Seismic Experiment [J]. J Geophys Res, 104(B11): 25543-25565.
- Matheney M P, Nowack R L. 1995. Seismic attenuation values obtained from instantaneous-frequency matching and spectral ratios [J]. Geophys J Int, 123(1): 1-15.
- Mayne W H, Quay R G. 1971. Seismic signatures of large air guns [J]. Geophysics, 36(6): 1162-1173.
- Okaya D, Henrys S, Stem T. 2002. Double-side onshore-offshore seismic imaging of a plate boundary: “super-gathers” across South Island, New Zealand [J]. Tectonophysics, 355(1-4): 247-263.
- Rilling G, Flandrin P. 2008. One or two frequencies? The empirical mode decomposition answers [J]. IEEE Transactions on Signal Processing, 56(1): 85-95.
- Stern T, Okaya D, Scherwath M. 2002. Structure and strength of a continental transform from onshore-offshore seismic profiling of South Island, New Zealand [J]. Earth Planets & Space, 54(11): 1011-1019.