基金项目:国家自然科学基金——基于竖向台阵记录数据的强震动作用下土非线性动力特征的实证研究(51578514)资助.
(Earthquake Administration of Yunnan Province,Kunming 650224,Yunnan,China)
Ludian earthquake; strong motion recordings; source parameters; displacement spectrum
备注
基金项目:国家自然科学基金——基于竖向台阵记录数据的强震动作用下土非线性动力特征的实证研究(51578514)资助.
通过对2014年鲁甸MS6.5地震13个强震动台站观测记录的谱分析,估算了地震矩、矩震级等震源参数,得到的平均矩震级MW=6.3。讨论了震源Brune模型位移谱形状系数以及局部场地条件对估算参数的影响,结果显示,谱形状系数对参数估算影响不大,但ω2和ω3源谱模型分别能与远场和近场记录获取的源谱吻合更好; 同时,仅在场地的卓越频率小于1 Hz时,场地条件影响参数的估算,由于13个台站均处于Ⅰ~Ⅱ类场地上,局部场地条件对本文参数计算结果影响不大。
Through spectrum analysis of observation recordings of Ludian MS6.5 earthquake in 2014 recorded by 13 strong motion station,we estimated the source parameters of the earthquake such as seismic moments,moment magnitude,corner frequency etc.and obtained the average moment magnitude MW=6.3.Then we discussed the influence of the displacement spectrum shape coefficients of the Brune source model and the local site condition on the source parameter estimation.The results show that the influence of the spectrum shape coefficients on the source parameter estimation is small,but source spectrum model ω2 and ω3 fit the source spectrums of recordings from far site and near-site separately.At the same time,only when the predominant site frequency is smaller than 1 Hz,the site condition could influence the source parameter estimation.The studied 13 stations are all located atⅠand Ⅱ sites,so the local site condition does not influence the results of the source parameter estimation.
引言
震源参数谱分析(Boatwright,1978,1980; 黃明伟,2006)是个被广泛应用的方法,在云南地区,秦嘉政等(2003,2005)、叶建庆等(2007)应用该方法研究了发生于云南的多个地震序列,对地震特征获得了有益的认识。2014年8月3日,云南省鲁甸县发生MS6.5强烈地震,震中位置(27.1°N,103.3°E),震源深度12 km。分布于震区及其周边地区的80多个强震动台站获取了主震记录(崔建文等,2014)。本次地震发生在两条断层的交汇处,具有较为复杂的震源过程(Li et al,2015; 张勇等,2015),对这次地震更深入的了解,有赖于获取震源的更多信息。本文从80多个强震动记录中,选取部分信噪比较高的记录,采用震源参数谱分析方法计算震源参数(地震矩M0、矩震级MW、拐角频率fC以及断层尺度等),其结果有助于加深对本次地震的物理过程、震源特征认识。
1 数据
各地震监测机构给出的鲁甸MS6.5地震震级及震中位置不尽相同(表1),中国地震台网中心(CENC)给出的震中位置与云南地震台网中心结果是一致的,只是前者给出的数据精度仅到小数点后1位,USGS虽然也给出高精度的震中坐标,但从现场破坏情况看,其坐标位置偏离了极震区,后期开展的一些地震定位工作(徐甫坤等,2014; 何骁慧等,2015; 王未来等,2014; 张广伟等,2014; 赵小艳,孙楠,2014)均给出了与云南地震台网中心相近的震中坐标,但震源深度从9.5 km到15 km不等,有明显差距。张广伟等(2014)采用gCAP方法,得到震源最佳质心深度为5 km,其双差分定位的震源深度是13.3 km,前者反映了地震破裂面的质心深度,代表了地震能量的集中点,后者是地震破裂的开始点,表明地震由较深的位置开始破裂,然后向浅部发展,与张勇等(2014,2015)的震源破裂过程相一致。
表1 鲁甸MS6.5地震参数
Tab.1 Parameters of Ludian MS6.5 earthquakes在后面参数的计算中,采用的是记录中完整的SH波,其对应的应该是地震能量的集中点,采用破裂面质心作为震源应该更合理,其深度为5 km。
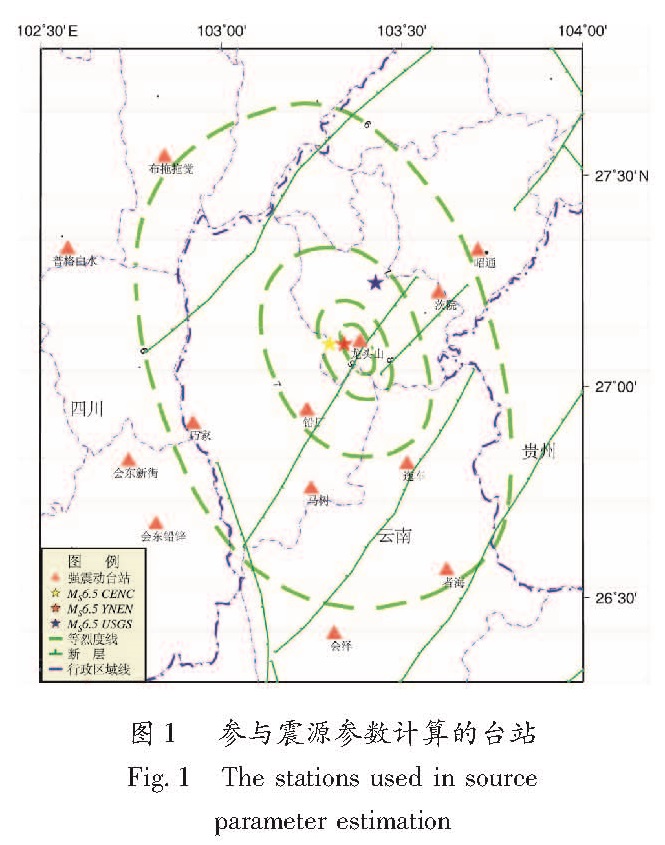
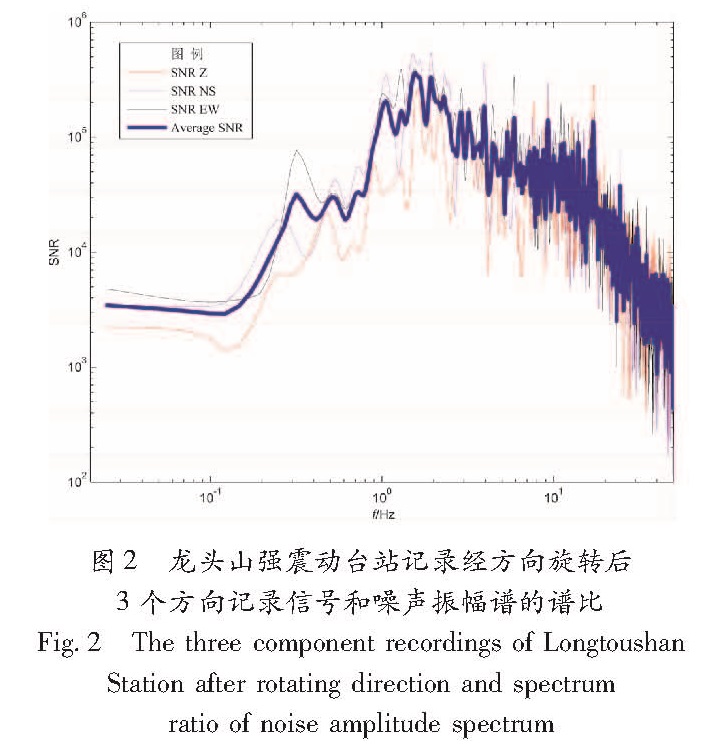
为获取可靠的震源参数,使用的记录应该具有高的信噪比(SNR),尤其在低频段。本文计算了震中距在100 km以内的台站记录的信噪比,在0.03~25 Hz的频带内,选取了SNR值大于100的记录参与计算,最终选择13个台站的记录,台站情况见表2。图1显示了所选取台站的分布,可以看到,除震中上方NNW—NNE方位以外,其他方位均有台站环绕震中分布。图2是鲁甸龙头山强震动台站记录的信噪谱比,图3是13个台站记录的信噪谱比,龙头山强震动台站记录具有非常高信噪比,其SNR值大于1 000。
图2 龙头山强震动台站记录经方向旋转后
3个方向记录信号和噪声振幅谱的谱比
Fig.2 The three component recordings of Longtoushan Station after rotating direction and spectrum ratio of noise amplitude spectrum2 源参数计算方法
台站获取的地震动S波的傅里叶频谱AS(f)可表示为(黄明伟,2006)
AS(f)=A(f)·G(R)·S(f)·I(f)·exp(-c(f)R).(1)
式中,f为频率,R为台站到震源的距离,A(f)为震源的地震动(加速度、速度和位移)傅里叶谱,G(R)为地震动的几何扩散效应,S(f)为场地响应,I(f)为仪器响应,c(f)是介质的非弹性衰减系数。
获取台站地震动记录后,震源的地震动S波傅里叶频谱可表示为
A(f)=(AS(f)·exp(c(f)R)·I(f))/(G(R)·S(f)).(2)
对于震源地震动S波,其位移和速度的傅氏振幅谱D(f)、 V(f)可近似表示为(Brune,1970)
表2 参与震源参数计算的强震动台站概况
Tab.2 Basic parameters of strong motion stations used in source parameter estimationD(f)=(Ω0)/(1+(f/fc)n),(3)
V(f)=(2πfΩ0)/(1+(f/fc)n).(4)
式中,fc为拐角频率,Ω0为震源位移谱零频极限值,n是控制谱形状的常数。对实际观测的台站地面运动加速度记录,经积分获取速度、位移时程,通过式(2)消除几何衰减、场地响应和介质非弹性耗损等影响因素后,可得到震源的地震动位移和速度的傅里叶谱D0(f)、 V0(f),相应的振幅谱|D0(f)|、 |V0(f)|曲线可用式(3)、(4)进行拟合,从而可确定式中的参数Ω0、fc。
确定了Ω0、fc之后,可确定地震矩M0=4πrρβ3Ω0/Rθφ、震源的等效位错半径γ=(2.34β)/(2πfc)、断层破裂面积A=πγ2、位错U=(M0)/(μA)、应力降Δσ=(7M0)/(16γ3)等参数。其中,r为台站到震源的距离,ρ=2.8 g/cm3为介质密度,β为剪切波速度,Rθφ为辐射因子,取为0.63,μ=3.4×104 MPa为剪切模量。
进一步可确定矩震级MW为(Kanamori,1977)
MW=2/3lgM0-10.7.(5)
3 数据处理及结果
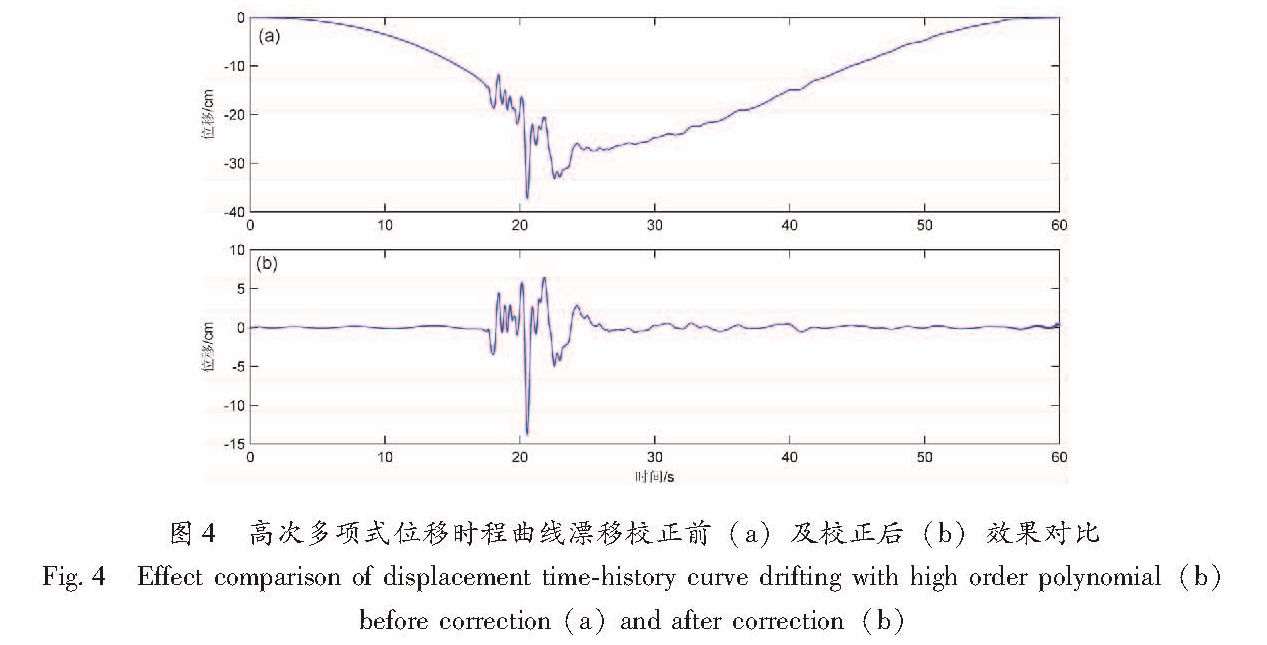
3.1 记录时程积分及旋转强震动加速度记录经一次积分得到速度时程,经两次积分得到位移时程。两次积分获取位移时程时存在着严重的漂移(Akkar,Boore,2009)。目前,已有多种消除漂移的方法(Akkar,Boore,2009; Chiu,2012,Huang et al,2013),其中,高通滤波是最常用也非常有效的方法,但会丢失在震源参数谱分析法中最具价值的低频信息,采用多项式拟合方法消除地震动时程中存在的趋势项,可以在保留地震动低频信息的同时,解决加速度时程积分产生的漂移问题。图4显示了采用高次多项式拟合消除时程趋势的效果,图4a是鲁甸地震龙头山台的东西向未进行漂移校正的位移记录,图4b是经过21次多项式趋势校正的位移记录,可以看到,大的趋势漂移已经基本消除。实际处理时,多项式的次数根据漂移的程度选择。
对记录进行谱分析时,选用记录的SH波,为此,将2个记录水平向旋转到地震波传播方向(径向R)及垂直地震波传播的方向(切向T),并从切向记录中选择SH波。图5显示了位移时程曲线方位角旋转前后及SH波选取情况。
图4 高次多项式位移时程曲线漂移校正前(a)及校正后(b)效果对比
Fig.4 Effect comparison of displacement time-history curve drifting with high order polynomial(b)before correction(a)and after correction(b)3.2 影响校正将观测的地面运动谱还原到震源的运动谱,需进行仪器、传播路径和局部场地影响的校正。由于获取记录的强震动仪的幅频特性曲线在0~200 Hz内是值为1的平坦直线,在本文讨论的频带内不需进行仪器的影响校正。
传播路径的影响包括波的几何扩散和非弹性衰减。几何扩散效应校正采用Atkinson和Mereu(1992)的模型:
G(R)={r-b1, r≤r1;
rb2-b11r-b2, r1≤r<r2;
rb2-b11r2b3-b2r-b3, r2≤r.(6)
式中,r为震源距,并且取b1=1.0,b2=1.0,b3=1.0,r1=60 km,r2=100 km(Lam,2000; 阮祥,2007)。
对云南东部地区,苏有锦等(2006)研究得到的介质非弹性品质因子Q=199.6f 0.434,则在式(1)中取c(f)=(πf)/(Q(f)β)可对获取的位移时程频谱进行介质的非弹性衰减校正,其中β为剪切波速。
局部场地的校正需要场地的频率响应,但由于场地响应在1 Hz以上时才有较明显的效应,主要影响高频成分,对于1 Hz以下的地震动影响有限,因此,这里不做考虑,后面结合实际数据分析结果,讨论其影响。
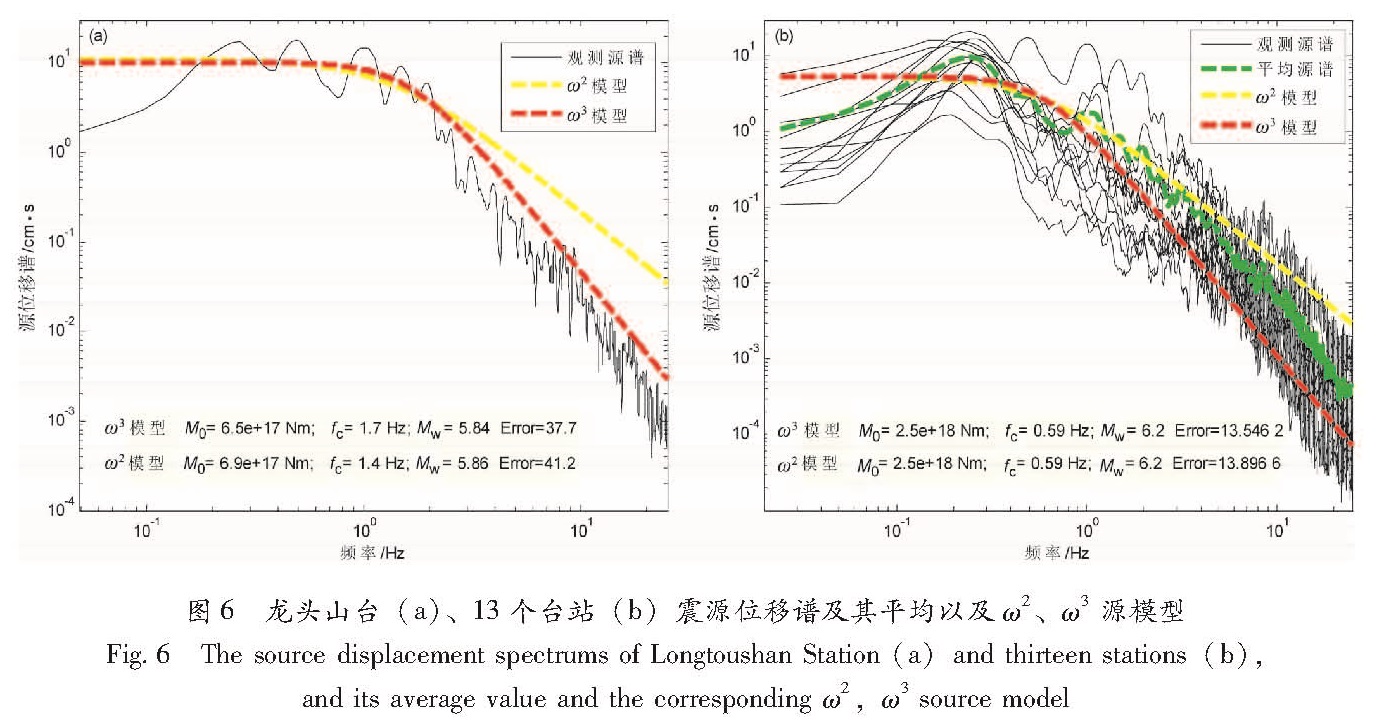
3.3 数据处理结果对13个时程记录进行方位角旋转、积分、漂移校正以及各种影响校正,对选取的SH波进行5%Cosine Taper的矩形窗处理。对选取的速度、位移时程SH波作傅氏变换,可得到震源的速度、位移傅氏振幅谱,用式(3)拟合震源位移傅氏振幅谱,确定Ω0、fc。拟合时,对式(3)中的控制形状的常数n,同时取2、3两种情况,并采用遗传算法搜寻使拟合误差最小的Ω0、fc,进而计算地震的矩震级MW、地震矩M0、应力降Δσ等源参数。这里,以震中龙头山台记录为例,图6a显示了该台站位移源谱及其拟合情况。表3是由各个观测台站估算的MS6.5主震的震源参数,可以看到,利用各台站记录计算得到的震源参数有差异,最终结果通过平均13个台站的结果得到。为消除个别台站的异常值,采用了Archuleta方法(王生文等,2014)计算平均值,其计算公式为
{x=exp(1/N∑Ni=1lnxi),
Δx=exp((1/(N-1)∑Ni=1(lnxi-lnx))1/2).(7)
式中,xi为第i个台站的参数,x为Archuleta平均值,Δx为对应的标准差。
此外,可在频域里计算各台站源谱的平均值,再进行Brune源模型拟合求相关参数。图6b显示了13个台站的源谱线、其平均谱曲线以及拟合的源谱。
ω2模型和ω3模型给出的源参数非常相近,相应的结果列于表3中(表中仅列出了ω3模型的结果)。
图6 龙头山台(a)、13个台站(b)震源位移谱及其平均以及ω2、ω3源模型
Fig.6 The source displacement spectrums of Longtoushan Station(a)and thirteen stations(b),and its average value and the corresponding ω2,ω3 source model4 讨论
4.1 结果分析从表3可以看到,13个台站之间参数估计结果有差异,就地震矩、矩震级、拐角频率而言,除龙头山台站以外,其他台站的离散性较小,平均矩震级MW=6.3,与实际情况相吻合; 但震源的等效位错半径、应力降、断层位错等参数离散较大,其原因在于,震源的等效位错半径对拐角频率较敏感,后者的较小变化将导致前者较大的变化,而应力降、断层位错等其他参数均与震源的等效位错半径的平方、三次方成正比或反比,小的拐角频率差异在应力降等参数中得到了相当程度的放大。导致各台站估计结果差异的因素有很多,如信噪比、拟合方法等,而台站的震中距、方位的分布也应该是因素之一。在一个方位上,估计值也许会偏大,而在另一个方位上,也许会偏小,因此,如果能拥有在震中距、方位角上完善分布的台站,则这些台站的估计值的平均值应该能接近于期望的结果。本文13个台站分布在除震中上方NNW—NNE方位以外其它方位和震中距上,较好地包含了方位角、震中距影响的信息,13个台站估计值的平均应能较好地消除各台站因方
表3 由强震动观测记录估算的MS6.5主震的震源参数(ω2、ω3模型)
Tab.3 The source parameters of MS6.5 main shock estimated from strong motion observation recordings(ω2、ω3 model)位角、震中距影响导致的估值偏差。
龙头山台的估计值矩震级明显偏小、拐角频率明显偏大,这可能与该台非常靠近震源而与Brune模型的远场假定不符有关,此外普格白水台的矩震级估计结果也明显偏小,但拐角频率估值合理,其原因有待探讨。
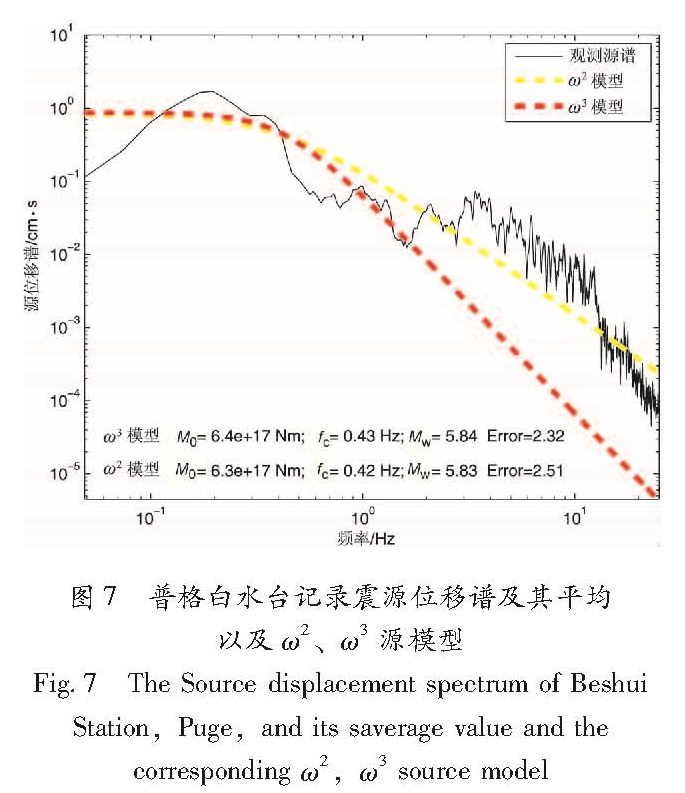
4.2 Brune源谱模型常系数n的影响在Brune源谱模型式(3)中,虽然大量的研究都支持谱形状控制常数n取为2,即称之为ω2模型(Chael,1987; Shearer,1999),但也有许多研究认为震源谱为ω3模型(Savage,1972)或其它模型(Boatwright,Choy,1992; Joyner,1984; Atkinson,Silva,1997)。本文同时采用了ω2和ω3模型进行参数计算,对于所有参与计算的台站,2种模型都给出了几乎相同的参数,即模型的基本选择不影响fc、M0和MW等主要震源参数的估计。图7是13个台站中震中距最大的台站的震源谱及其拟合情况,可以看到,在频率高于2 Hz以后,ω2模型与观测谱吻合比ω3模型更好,而在震中距很小的图6a显示的频率范围内,ω3模型比ω2模型更符合实际。就13个台站采用ω2和ω3模型的拟合效果而言,随着震中距的增加,在高频段,好的拟合效果逐渐由ω3模型过渡为ω2模型。因此,近场宜用ω3模型,远场宜用ω2模型。
4.3 场地影响局部场地对地震动有强烈影响,一般情况下,基岩上的覆盖土层放大地震动,用这种受到影响的记录来估计源谱参数,必然会影响参数估计的结果。但这种影响有多大,是否会导致结果出现重大的偏差,则是个值得探讨的问题。从表3可以看到,13个台站得到的MW有较大的离散性,如果通过场地影响校正可以降低这种离散性,则这种校正就具有较大的价值。
在以拟合误差为控制的观测源谱与Brune模型拟合估计源谱参数时,低频成分(小于1 Hz)远远大于高频成分,因此低频成分起主导作用,高频成分的变化不影响拟合结果,采用ω2和ω3模型得到相近的结果能很好地说明这一结论。因此,如果说场地效应只对高频成分产生影响,则不进行场地影响校正并不影响源谱参数的估计结果,但如果场地对低频成分有影响, 则就必须进行场地校正。局部场地对地震动的影响虽然是个复杂的问题,但还是有规律可循,在Ⅰ~Ⅳ类场地中,场地卓越周期由小变大,对应着对地震动频率成分的影响由高频逐渐向低频过渡,场地的卓越周期大约为T=4H/vS(H为场地土层厚度,vS为土层剪切波速),则按照建筑抗震设计规范(GB50011—2010),Ⅰ类场地的卓越频率约大于12.5 Hz,Ⅱ类场地的在3~12.5 Hz范围内,Ⅲ类场地的在0.47~3 Hz之间,Ⅳ类场地的小于0.47 Hz。因此,Ⅰ、Ⅱ类场地的场地效应不会影响源谱参数的估计,部分Ⅲ类场地有影响,而Ⅳ类场地有大的影响。本文中13个台站,其场地类型大部分为Ⅱ类,仅有昭通台和铅厂台为Ⅰ类,进行场地校正并不能改善参数估计的结果。
图7 普格白水台记录震源位移谱及其平均以及ω2、ω3源模型
Fig.7 The Source displacement spectrum of Beshui Station,Puge,and its saverage value and the corresponding ω2,ω3 source model5 结论
本文基于鲁甸地震13个强震动台站获取的强震动观测记录,应用震源参数的谱分析方法估计主震的地震矩、矩震级、拐角频率等。结果表明,13个台站参数估计的平均值可给出合理的结果,矩震级MW的估计平均值为6.3。除龙头山台站外,其它台站频率拐角值差异不大,但基于拐角频率计算的其它参数,较大程度对拐角频率的差异进行了放大,导致了13个台站的应力降、震源的等效位错半径等参数的估计值之间有较大的离散性。除改进方法外,采用多个能很好地环绕震中分布的台站可改善参数估计的效果。
进行谱曲线拟合估计参数时,无论采用ω2还是ω3模型,结果均相近,但近场时,宜采用ω3模型,远场时ω2更好。
仅在台站场地为Ⅲ、Ⅳ类时场地效应会影响源参数的估计,在场地为Ⅰ、Ⅱ类时,可不进行场地影响的校正。
两位匿名审稿专家对本文提出了许多建设性的修改意见,部分图件采用了GMT软件绘制,笔者在此表示衷心地感谢。
- 崔建文,刘琼仙,段建新.2014.2014年云南鲁甸6.5级地震强震动观测记录及初步分析[J].地震研究,37(4):542-548.
- 何骁慧,倪四道,刘杰.2015.2014 年8 月3 日云南鲁甸M6.5 地震破裂方向性研究[J].中国科学:地球科学,45(3):253-263.
- 黃明偉.2006.使用强震动记录估算1999年集集大地震余震之辐射能量与地震力矩[D].台湾:国立中央大学地球物理研究所.
- 秦嘉政,钱晓东,叶建庆.2005.2001年施甸MS5.9地震序列的震源参数研究[J].地震学报,27(3):250-259.
- 秦嘉政,叶建庆,钱晓东.2003.2000年云南姚安地震的震源参数[J].地球物理学报,46(4):633-641.
- 阮祥.2007.川滇中小地震震源参数的研究[D].兰州:中国地震局兰州地震研究所.
- 苏有锦,刘杰,郑斯华等.2006.云南地区S波非弹性衰减Q值研究[J].地震学报,28(2):206-212.
- 王生文,李艳娥,郭祥云等.2014.1999年11月29日岫岩MS5.4地震序列视应力的再研究[J].地震,34(3):50-61.
- 王未来,吴建平,房立华等.2014.云南鲁甸地震序列的双差定位[J].地球物理学报,57(9):3042-3051.
- 徐甫坤,李静,苏有锦.2014.2014年云南鲁甸6.5级地震序列重定位研究[J].地震研究,37(4):241-247.
- 叶建庆,张建国,杨晶琼等.2007.红河断裂带两侧地块地震震源参数研究[J].地震研究,30(3):241-247.
- 张广伟,雷建设,梁姗姗等.2014.2014年8月3日云南鲁甸6.5级地震序列重定位与震源机制研究[J].地球物理学报,57(9):3042-3051.
- 张勇,陈运泰,许力生等.2015.2014年云南鲁甸MW6.1地震:一次共轭破裂地震[J].地球物理学报,5(1):153-162.
- 张勇,许力生,陈运泰等.2014.2014年8月3日云南鲁甸MW6.1(MS6.5)地震破裂过程[J].地球物理学报,57(9):3052-3059.
- 赵小艳,孙楠.2014.2014 年云南鲁甸6.5级地震震源位置及震源区速度结构联合反演[J].地震研究,37(4):523-531.
- Akkar S,Boore D M.2009.On baseline corrections and uncertainty in response spectra for baseline variations commonly encountered in digital accelerograph records[J].Bull Seism Soc Am,99(99):1671-1690.
- Atkinson G M,Mereu R F.1992.The shape of ground motion attenuation curve in Southeastern Canada[J].Bull Seism Soc Am,82(5):2014-2031.
- Atkinson G,Silva W.1997.An empirical study of earthquake source spectra for California earthquakes[J].Bull Seism Soc Am,87(1):97-113.
- Boatwright J,Choy G L.1992.Acceleration source spectra anticipated for large earthquakes in northeastern North America[J].Bull Seism Soc Am,82(2):660-682.
- Boatwright J.1978.Detailed spectral analysis of two small New York state earthquakes[J].Bull Seism Soc Am,68(4):1117-1131.
- Boatwright J.1980.A spectral theory for circular seismic sources:Simple estimates of source dimension,dynamic stress drop and radiated seismic energy[J].Bull Seism Soc Am,70(1):1-27.
- Brune J N.1970.Tectonic stress and spetra of seismic shear wave from earthquake[J].J Geophys Res,75(4):4997-5009.
- Chael E P.1987.Spectral scaling of earthquakes in the Miramichi region of New Brunswick[J].Bull Seism Soc Am,77(2):347-365.
- Chiu H-C.2012.A Compatible Baseline Correction Algorithm for Strong-Motion Data[J].Terr Atmos Ocean Sci,23(2):171-180.
- Huang J Y,Wen K L,Li X J,et al.2013.Coseismic Deformation Time History Calculated from Acceleration Records Using an EMD-Derived Baseline Correction Scheme:A New Approach Validated for the 2011 Tohoku Earthquake[J].Bull Seism Soc Am,103(2B):1321-1335.
- Joyner W B.1984.A scaling law for the spectra of large earthquakes[J].Bull Seism Soc Am,74(4):1167-1188.
- Kanamori H.1977.The energy release in great earthquakes[J].J Geophys Res,82(20):2981-2987.
- Lam N T K,Wilson J L,Hutchinson G L.2000.Generation of synthetic earthquake accelerograms using seismological modeling:a review[J].Journal of Earthquake Engineering,4(3):321-354.
- Li X,Xu X W,Ran Y K,et al.2015.Compound Fault Rupture in the 2014 MS6.5 Ludian,China,Earthquake and Significance to Disaster Mitigation[J].Seismological Research Letters,86(3):764-774.
- Savage J C.1972.Relation of corner frequency to fault dimensions[J].J Geophys Res,77(20):3788-3795.
- Shearer P M,1999.Introduction to Seismology[M].NewYork:CambridgeUniversityPress,16.
- GB50011—2010,建筑抗震设计规范[S].