基金项目:国家自然科学基金(51408040)资助.
(School of Highway,Chang'an University,Xi'an 710064,Shaanxi,China)
cable-stayed bridge; vulnerability analysis; injury calibration; exceedance probability
备注
基金项目:国家自然科学基金(51408040)资助.
以某大跨斜拉桥为例,利用SAP2000建立有限元模型,基于结构性能目标,探讨桥梁构件损伤标定方法,并采用IDA的倒塌易损性分析方法,对该斜拉桥进行横向的地震易损性分析,最后采用能力需求比模型法拟合出主塔的易损性曲线。研究结果表明,在横向地震作用下,索塔墩顶截面、上塔柱底部成为易损截面的概率增大,连接主梁的中塔柱底部截面出现完全破坏的概率增大。
In this paper,based on a long-span cable-stayed bridge,a finite element model is established by using SAP2000.Based on structural objectives,we studied on calibration method for bridge structure damage.By using collapse vulnerability analysis method which is based on IDA,we analyze the lateral seismic fragility of cable-stayed bridge.Finally,the seismic fragility curves of the main tower can be fitted by using capacity requirement modeling method.The research indicate that under the transverse seismic waves,towers became more vulnerable at the section of top and the bottom of upper tower column.The bottom of mid tower connecting the girder tends to be completely destroyed.
引言
地震易损性分析主要预测在不同强度的地震波下,结构物超越各级破坏水平的概率。而易损性曲线则是将地震的危害性进行量化表达。对于重要线路上的桥梁,不仅期望在小震作用下不发生破坏,还要确保在大震作用下具有一定的通行能力,以满足应急救灾和灾后重建工作的需要。传统的地震易损性分析,最早起源于对核电站结构进行的地震危险性评估。公路桥梁的地震易损性分析则是以易损性曲线来表达,地震作用的强度不同,桥梁结构超过各级损伤指标的概率也存在差异,它可以直观表述桥梁结构的损伤情况(朱健等,2011)。
国际上,将地震易损性的研究划分为3个主要的阶段。第一阶段主要是采用调查和统计的方法获得统计意义上的结构易损性曲线(姚霄雯,2013)。Basoz和Kiremidjian(1997)、Kiremidjian和Bosoz(1997)根据Northridge地震后收集到的损伤数据,采取线性回归的方法拟合出了构件的经验易损性曲线,这就是最初的经验易损性分析方法。第二阶段是理论易损性分析方法。它主要是以概率和非线性方法对传统的损伤指标进行比较和统计计算,进而得到构件结构的易损性曲线。这种方法首先被Fukushima、Shinozuka等学者所采用(Fukushima et al,1996),并多用于简支梁桥和连续梁桥的概率评价。第三阶段是自2005年以后,随着多概率分析方法和多种新型分析方法的提出,对于结构试验数据评价不再局限于单一的某种方法,而是能够结合多种试验数据进行损伤评价。这种方法目前还处于探讨和发展阶段。
1 结构的地震易损性分析
1.1 易损性曲线建立流程早期的桥梁结构易损性研究主要采取比较实用的经验易损性分析方法。但该方法对于勘察到桥梁结构的样本数量不可控制,并且一些地区性的地震特征以及收集到的严重损伤或者倒塌的桥梁样本数量不足。这些缺点影响了该方法的进一步发展和应用。
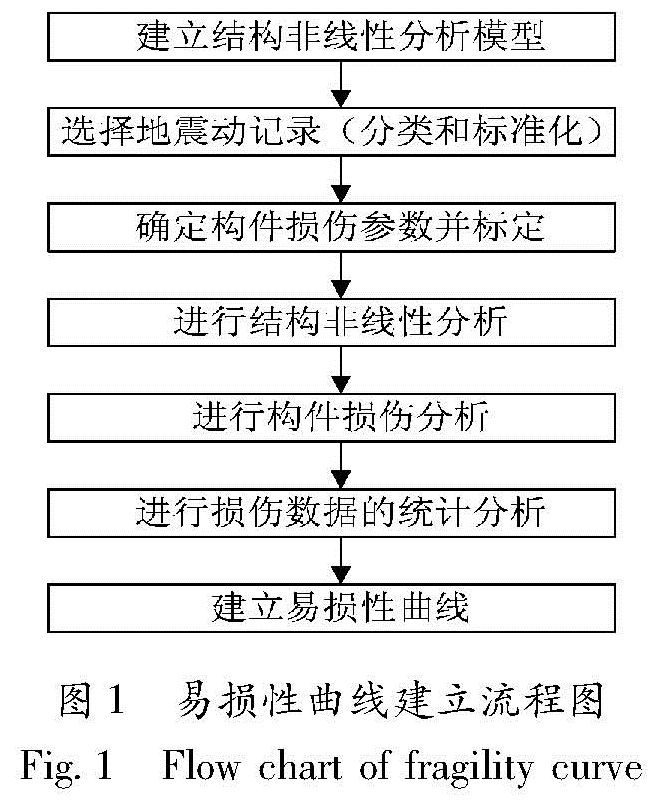
理论易损性分析方法是通过对桥梁结构的计算进行统计分析得到的。与早期的易损性研究方法相比,该方法可以更好地控制加载水平和实现对损伤参数的研究,其关键是绘制易损性曲线。常用的易损性曲线建立流程如图1所示。
1.2 易损性曲线拟合方法本文采用能力需求比模型法来拟合主塔的易损性曲线。它是将非线性时程分析所得结构的地震需求与所选损伤状态对应的损伤指标作比值,并将该比值与地震动强度描绘在对数正态坐标系中,最后在这个坐标系下进行最小二乘法的二次多项式回归,并求得回归标准差σ和均值μ。通过式(1)~(3),计算不同地震强度水平下超越某一损伤状态的失效概率,最终得到光滑的易损性曲线。
μ=a(ln(Sa))2+b(ln(Sa))+c.(1)
σ=(Sr/(n-2))1/2.(2)
Pf=P[(Sd)/(SC4)>1]=1-Φ((ln(l)-μ)/σ)=Φ(μ/σ).(3)
其中,n为回归的样本数,a、b、c为回归参数,Sr为回归分析的残差平方和。
1.3 桥塔结构的性能指标基于悬臂结构的损伤研究,对于高塔结构体系来说,仅仅对塔底截面进行评价分析是远远不够的,必须要从高塔的全部截面出发进行深入研究。目前主要用截面弯曲曲率来定义桥梁结构构件的损伤指标,因此本文决定采用截面不同层次的曲率指标作为斜拉桥主塔的损伤指标。根据众多研究人员的研究成果,可以选取钢筋混凝土的应变来表达基于性能的混凝土高塔截面的曲率损伤指标,并且通过对高塔截面进行P-M-φ分析来得到。表1给出了不同损伤状态下混凝土和钢筋应变所对应的截面曲率水平(朱红武,2005),可以根据该曲率水平定义本文主塔的损伤状态。
2 混凝土梁斜拉桥横桥向地震易损性分析
2.1 工程概况本文以马桑溪大桥为工程背景,探讨其主塔及辅助墩的损伤破坏过程。该桥位于巴南区花溪镇先锋村与大渡口区马桑溪之间,与东西立交和城区各干线连接,跨越成渝铁路,距李家沱长江大桥6 km。主桥采用双索面漂浮体系,主跨360 m,整体布置如图2所示。引桥采用简支梁桥。东西侧分别采用U型和L型钢筋混凝土桥台。
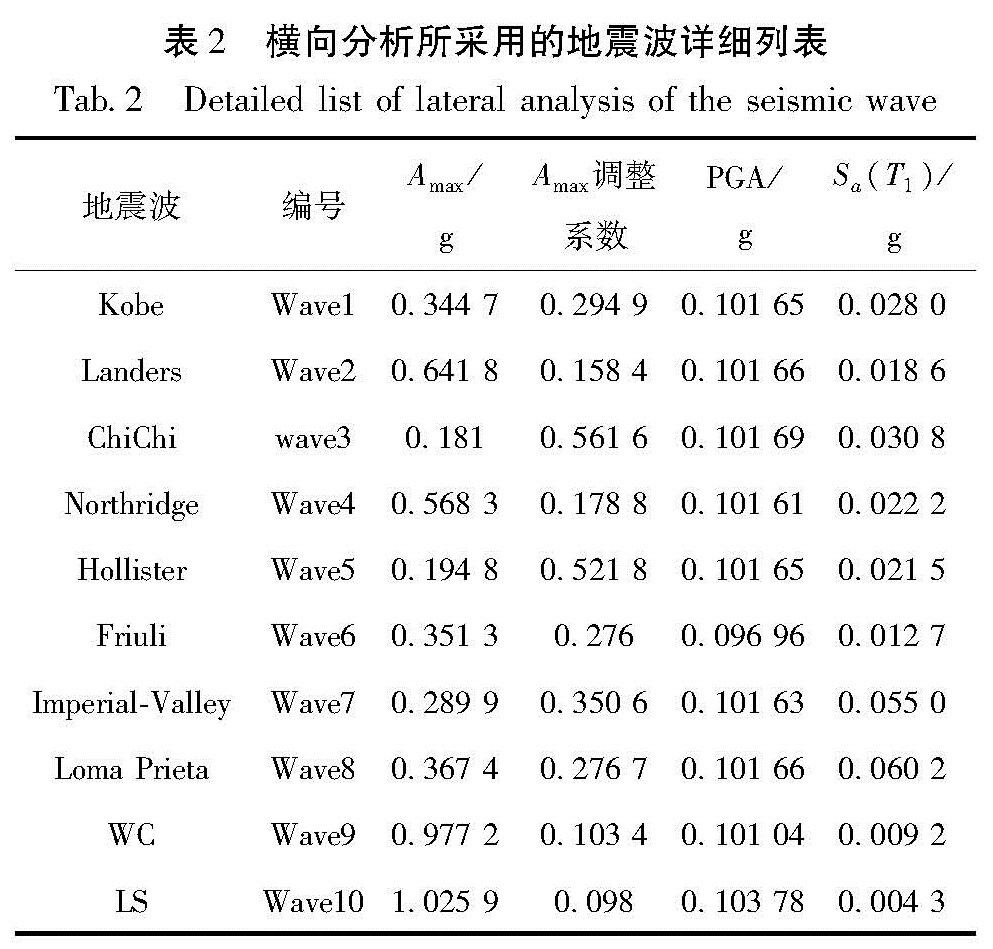
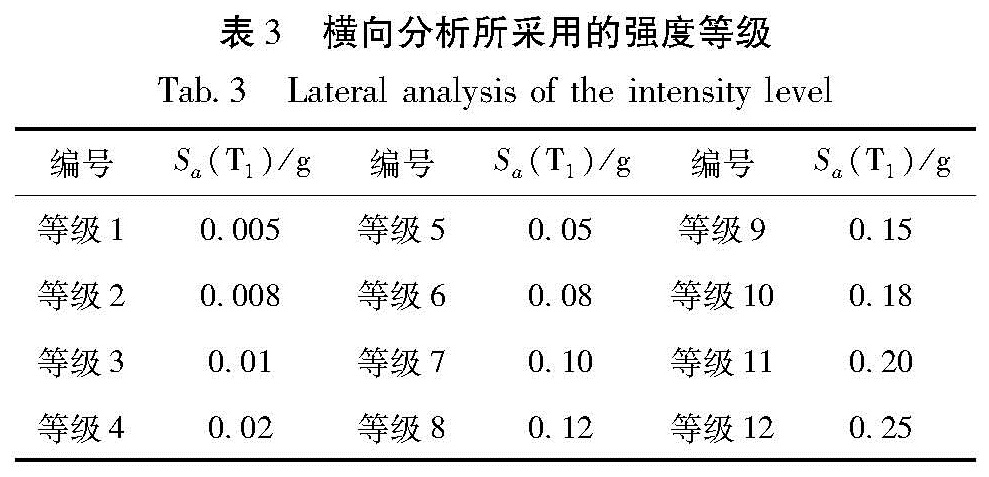
2.2 地震波输入本文选用10条地震波对马桑溪长江大桥(季正迪,2016)进行IDA分析。当周期T2=2.54 s时,横桥向的质量贡献率达到最大,因此选取此周期对应的反应谱加速度Sa作为强度指标,以实现降低横向地震需求离散性的目的。表2是10条地震波的详细情况汇总。表3对地震波的强度等级进行了适当的调整。
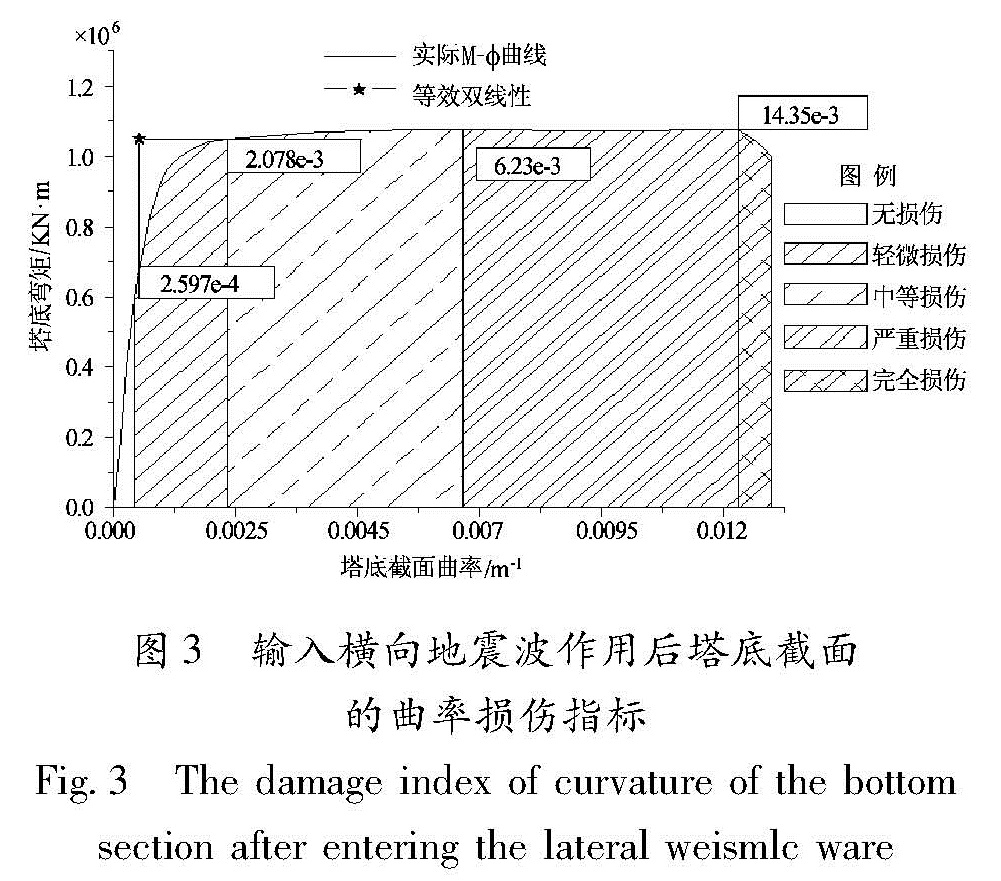
2.3 各构件损伤标定首先通过SAP2000计算出截面的最不利轴力,然后根据轴力与弯矩之间的关系求出截面的弯矩-曲率曲线如图3所示。根据等效双线性模型求出截面的四种损伤曲率进行标定。从图中可以看出,当曲率为0.000 259 7(1/m)时,截面出现轻微损伤; 当曲率为0.002 078(1/m)时,截面已发展到中等损伤; 当曲率为0.006 23(1/m)时,截面出现可严重破坏; 当曲率为0.014 35(1/m)时,截面已经完全破坏。
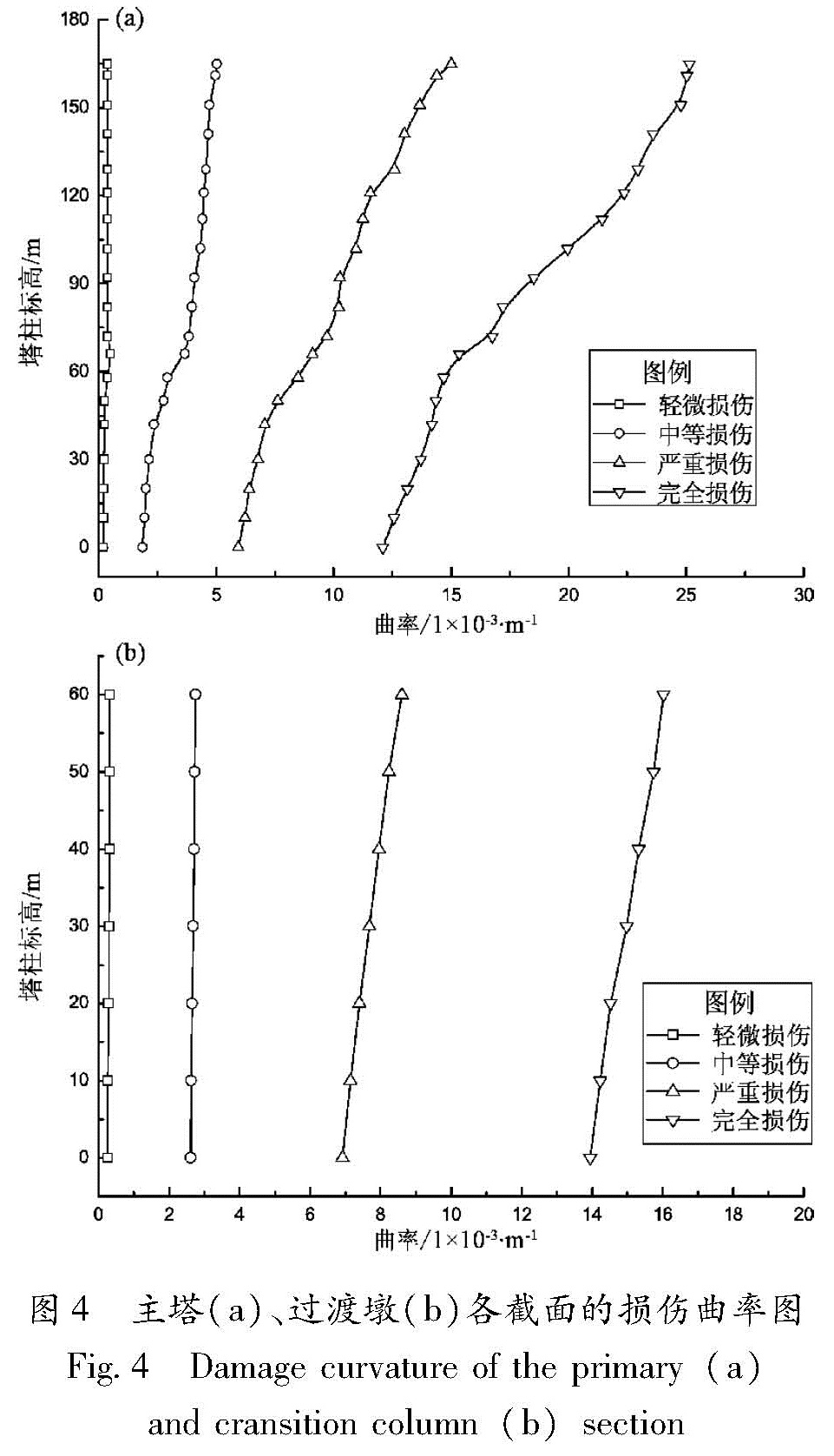
分析主塔各截面的M-φ曲线,图4是沿主塔及过渡墩标高方向各截面的损伤曲率图。
图3 输入横向地震波作用后塔底截面的曲率损伤指标
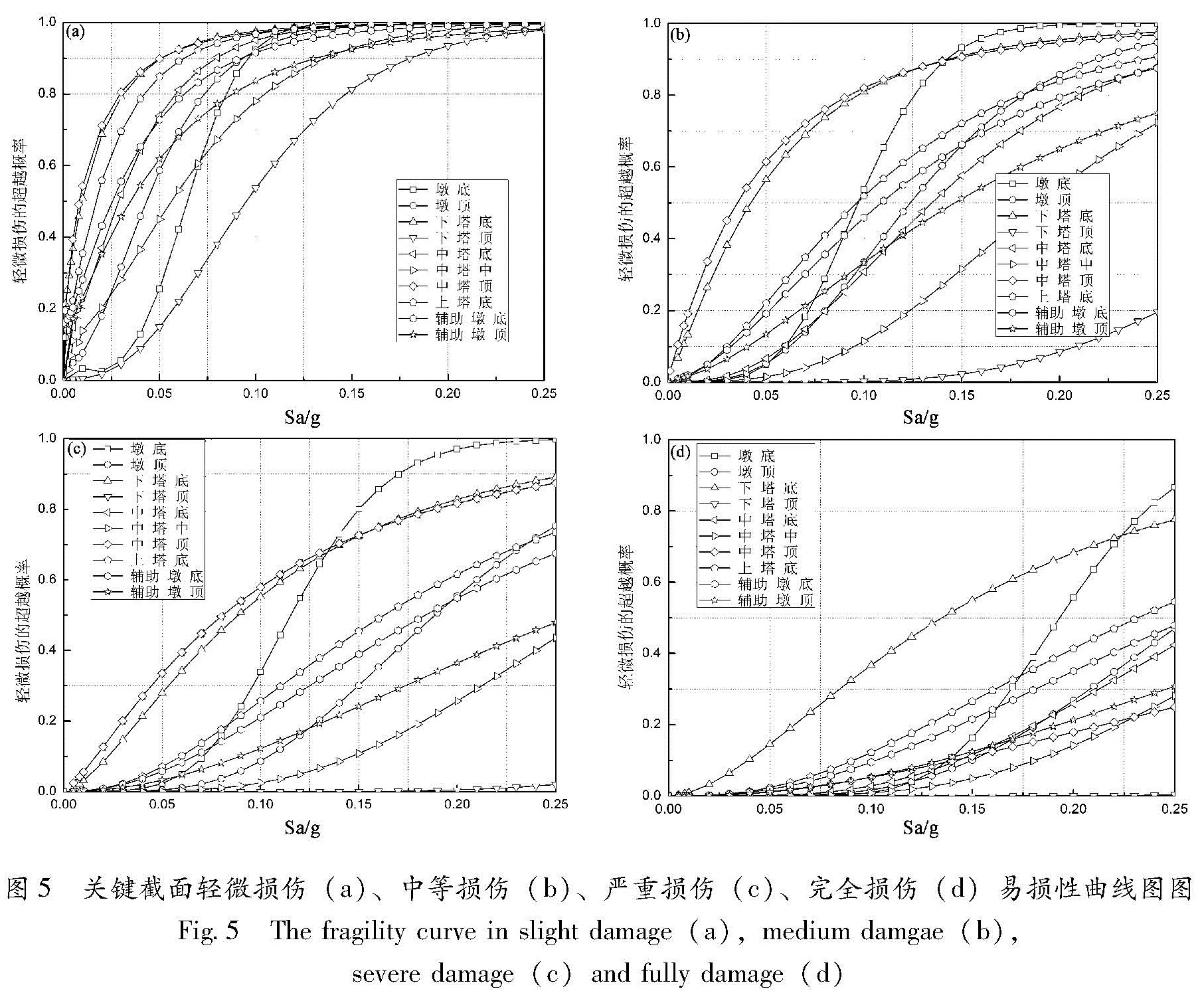
Fig.3 The damage index of curvature of the bottom section after entering the lateral weismlc ware2.4 关键截面易损性分析根据能力需求比模型法求出主塔及过渡墩截面在不同强度的地震作用下出现4种损伤的概率曲线。为了更加清楚地认识主塔截面及过渡墩截面在地震作用下的损伤情况,下面将不同截面在同一损伤状态的概率曲线进行对比,分析其在地震作用下的易损情况。图5为各个截面在不同地震波作用下对应的4种损伤概率曲线。
3 结论
本文利用SAP2000对马桑溪长江大桥进行横向地震波作用下的IDA分析,考虑地震强度的变化对主塔截面曲率的影响,利用能力需求比模型法绘制主塔及过渡墩截面在横向地震波作用下截面不同损伤状态下的超越概率曲线,可以得出下列主要结论:
(1)主塔及过渡墩在横向地震波作用下进入严重破坏的概率由大到小依次是:墩底>下塔柱底部>中塔柱顶部>墩顶>上塔柱底部>辅助墩底>中塔柱底部>过渡墩顶部>中塔柱中部>下塔柱顶部。
(2)在同一强度地震动作用下,主塔截面发生轻微破坏的概率远大于发生中等破坏的概率,这表明主塔截面在地震动作用下的安全储备充足。
(3)在横向地震作用下,墩顶截面、上塔柱底部成为易损截面的概率增大,墩底截面、下塔柱底部截面、中塔柱顶部截面仍然是易损截面,连接主梁的中塔柱底部截面出现完全破坏的概率增大。
- 季正迪.2016基于性能的混凝土斜拉桥地震易损性分析[D].西安:长安大学.
- 姚霄雯.2013.基于性能的高拱坝地震易损性分析与抗震安全评估[D].杭州:浙江大学.
- 朱红武.2005.建筑结构损伤理论及地震损伤评估的研究[D].上海:同济大学.
- 朱健,谭平,周福霖.2011.土木工程动力易损性分析研究现状与展望[J].建筑科学,27(5):69,109-113.
- BASOZ N,KIREMIDJINN A S.1997.RisRassessment of bridges and highway systems from the Northridge earthquake[C].Proceedings of the National Seismic Conferenceon Bridges and Highways:“Progress in Research and Practice”.Sacramento,California,65-79.
- FUKUSHIMA.S,KDI Y,YASHIRO K.1996.Study on thefragility of system-part I:Structure withbrittle elements in its stories[C].Proceedings of 11th World Conference on Earthquake Engineering 1996.EI sever scienceltd.Oxford,United Kingdom,1:333-339.
- KARIM K R,YAMAZAKI F A.2003.Simplified method ofconstructing fragility curves for bridges[J].Earthquake Engineering and Structural Dynamics,32:1603-1626.
- KIREMIDJIAN A A,BASÖZ N I.1997.Evaluation of bridge damage data from recent earthquakes[R].NCEER Bulletin,11(2):1-7.
- Riskassessment of bridges and highway systems fromthe Northridge earthquake[C].Proceedings of the National Seismic Conferenceon Bridges and Highways:“Progress in Research and Practice”.Sacramento,California,65-79.