震源空间位置的确定是地震学的经典问题——地震定位的一部分,也是地震学研究的基础。地震定位,无论是对于地球物理学研究,如地球内部的环境构造、地震的发生机制,还是对于震后救援工作的需求,如震害范围和程度的预估、地震趋势的预测以及地震预警,都有着无法替代的重要性。因此,地震定位的方法以及提高地震定位精度和速度的方法,一直都是地震学家的研究目标。

早期的地震定位主要是通过几何作图完成的。Geiger(1912)根据各个观测点到时差最小化的原则,将地震波走时方程组线性化,然后通过最小二乘法来定位地震。这也为以后使用计算机来定位地震提供了基础。20世纪70年代后,伴随着现代计算机技术的发展,地震学家们基于Geiger的理论,给出了一系列地震地位的程序和算法(Lee,Lahr,1975; Klein,1978; Lienert et al,1986; Nelson,Vidale,1990),并根据实际应用中出现的问题,提出了相应的改进方法(Lienert et al,1986; Prugger,Gendzwill,1988)。随后,多事件定位方法(Douglas,1976; Crosson,1976; Spence,1980; Waldhauser,Ellsworth,2000)、基于距离残差的空间域定位方法(Romney,1957; Lomnitze,1977)和非线性的定位方法(Prugger,Gendzwill,1988; Thurber,1985; Tarantola,Valette,1982)也相继出现。震相、振幅,甚至是全波形的信息都被用于震源位置的确定(Engdahl,et al,1998; Warren,Shearer,2005; 罗艳等,2013; Zhao,Helmberger,1994; Zhu,Helmberger,1996)。

在地震定位的过程中,影响结果精度的因素大致有:观测系统的结构、速度结构的选取或假设、震相识别以及观测数据(包含观测点的空间位置)的读取和计算过程中产生的误差(朱元清,赵仲和,1997; 田玥,陈晓非,2002)。绝大多数时间域和空间域的定位方法,都需要使用某一组先验的速度结构。因此,该种方法中速度结构的选取,将直接影响到结果的误差水平。而通过波形信息来确定震源位置时,震相识别、震源机制解和地球结构模型的可靠性,将决定定位结果的可靠性。

本文将介绍一种基于地震波射线理论,且不需要先验速度结构的定位近震震源位置的方法——射线追踪法,并使用虚拟数据和一个真实震例对该方法进行了检验。

假设地球介质是水平均匀且各向同性的分层介质。根据惠更斯原理和地震波射线理论,一束地震波在传播时,射线和分层界面法线的夹角满足方程

(v₁)/(sinθ₁)=……=(v_j)/(sinθ_j)=……=(v_n)/(sinθ_n)=const(1)

其中:v_j和θ_j是射线在第j层的波速和夹角(震源所在位置为第n层,地表为第一层上边界)。将地表处的夹角和波速作为已知条件,则

θ_j=arcsin((v_j)/(v₁)sinθ₁)(2)

从(2)式可以看出,射线与法线的夹角只与地表入射角θ_n和当前波速与地表波速的比值v_j/v₁(记为r_j)有关。另一方面,对于一束从震源发出的射线i,其在第j层介质中的传播,符合方程

s_ij=Δh_j/tanθ_ij(3)

式中:s_ij和θ_ij分别代表射线i在第j层介质中的水平位移和与法线的夹角; Δh_j表示第j层的厚度。同时,对于射线i,满足方程

θ_ij=arcsin(r_jsinθ_i1)(4)

结合式(3),可得:

s_ij=Δh_j/tan(arcsin(r_jsinθ_i1))(5)

因此,震源到射线接收点(即观测点)之间的水平位移为:

S_i=∑ⁿ_j=1s_ij=∑ⁿ_j=1Δh_j/tan(arcsin(r_jsinθ_i1))(6a)

或

Si=∫H i0si(h)dh=∫H i01/tan(arcsin(r(h)sinθi1))dh

(6b)

其中:H_i代表震源深度。θ_i1和Pg波的偏振方向相关,可以通过观测得到; 而S_i和H_i代表着观测点和震源空间位置的矢量差。因此,我们可以得到关于震源空间位置F(x,y,h)和r(r₁,r₂,…r_n)的方程(组):

{((x_i-y)²+(y_i-y)²)^1/2-S_i=0

(h_i-h)-H=0(7)

其中:(x_i,y_i,h_i)为观测点i的空间位置。本文所介绍的方法,就是要找到一组(F,r),使(7)式成立,或者使等式两边的差值尽量小,从而实现震源的定位。

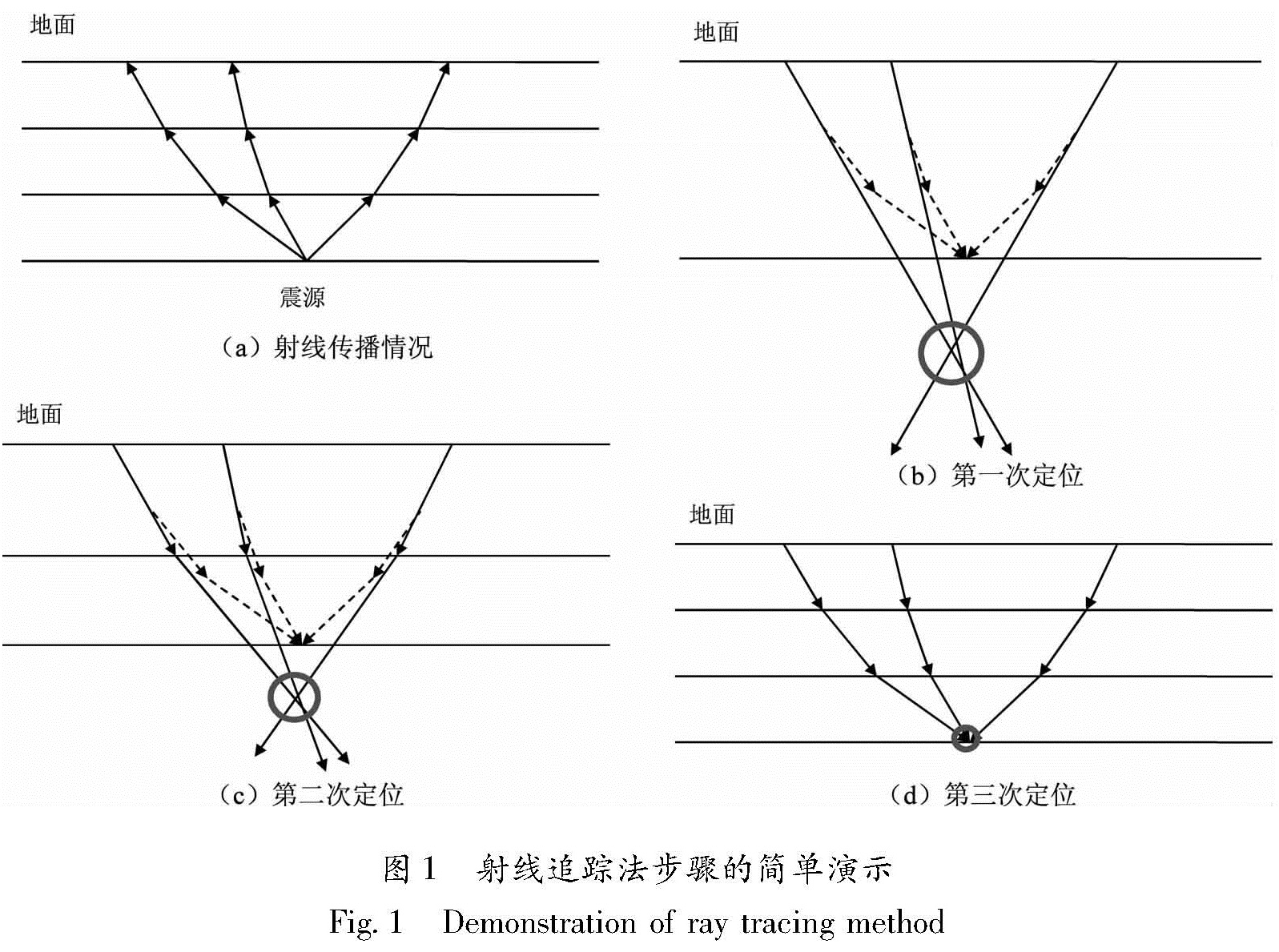
由于式(6)和(7)含有三角函数,不能采用线性方程组的方法来求解,而必须寻找一种合适的反演方法来确定(F,r)。网格搜索法是一种不错的方法,但是其计算量会随着参数的增加而呈指数增长。如果待求解的参数越多,则计算所花时间越长。因此,我们采用了一种“分步”的网格搜索法来定位震源,待求参数变少,计算效率得到了提升。图1是对这种方法的一个简单的展示,由于看起来像追溯射线的路径回到震源,我们称该方法为“射线追踪法”,其操作步骤如下:

(1)根据各个观测点接收到的Pg波的偏振方向,反向生成一组射线; 寻找到各条射线距离最短的一点F₁,并将其作为初始定位的结果(F₁,r₁)(r₁=1)。

(2)将介质平均分成2层,每层的厚度为h₁/2,r₁取步骤(1)的结果。使用网格搜索法,寻找第二层的波速比r₂,以及相应的点F₂,使F₂到根据(r₁,r₂)做出的反向射线的距离和最小。将(F₂,r₂)作为最新的结果;

(3)重复步骤(2),直到最后得到的结果(F_n,r_n)满足一定的收敛条件。F_n即为最终的定位结果。

通过射线追踪法,我们一步步将介质的分层数从2层增加至n层,且每一次分层都只用搜索新增层的波速比,从而大大减少了计算量。最终,我们会得到震源的位置F_n以及1组和各层相对应的波速比(r₁,r₂,…,r_n)。

为了验证此地震定位方法的准确性,本文虚拟了多组数据对该方法进行测试。测试数据生成

图1 射线追踪法步骤的简单演示
Fig.1 Demonstration of ray tracing method

的方法如下:

(1)选择1个一维速度模型作为基准模型,假定震中位置为0,震源深度为10 km。

(2)随机生成一组出射角为(θ_1n,…,θ_mn)的射线,根据步骤1的速度模型和震源位置,计算各条射线到达地表(深度为0)处的角度(θ₁₁,…,θ_m1)和震中距(S₁,…,S_m)。

(3)为(S₁,…,S_m)和(θ₁₁,…,θ_m1)引入误差,组成一组数据,分别对应m个虚拟观测点的坐标和接收到射线的Pg波偏振方向。

对于震中一定范围以外的观测点,Pg波的到达往往会晚于Pn波。此时,Pg波的振幅信息会和其它震相的信息混杂在一起,这就对Pg波偏振方向的确定造成了困难。因此,在生成测试数据时,要注意将θ值限定在一定的范围内。在本研究中,θ的取值范围分为3档,分别为≤ 30°、≤ 45°和≤ 60°,本文将对结果进行比较分析,以观察不同的出射角范围对定位精度的影响。同理,为了解观测误差和观测点数量对于定位精度的影响,本文也选取了相应的参数来进行测试。为了计算上的方便,我们将三维空间简化为二维,即去掉了一个水平维度,变成了如图1所示的情况。这样的简化并不会对测试造成本质性的影响。

本文共虚拟了14万组数据来进行测试,其详细信息见表1。所有的数据按照不同的观测点数量、出射角度范围、误差范围等因素分入14个大组,每个大组包含1万组数据。除观测点数量以外,生成每一组数据所用到的角度和误差都是在限定范围内随机生成的。显然,当误差水平为0,则意味着该组数据没有引入相应的误差。

表1 14个大组数据测试数据
Tab.1 Information of 14 groups of testing data

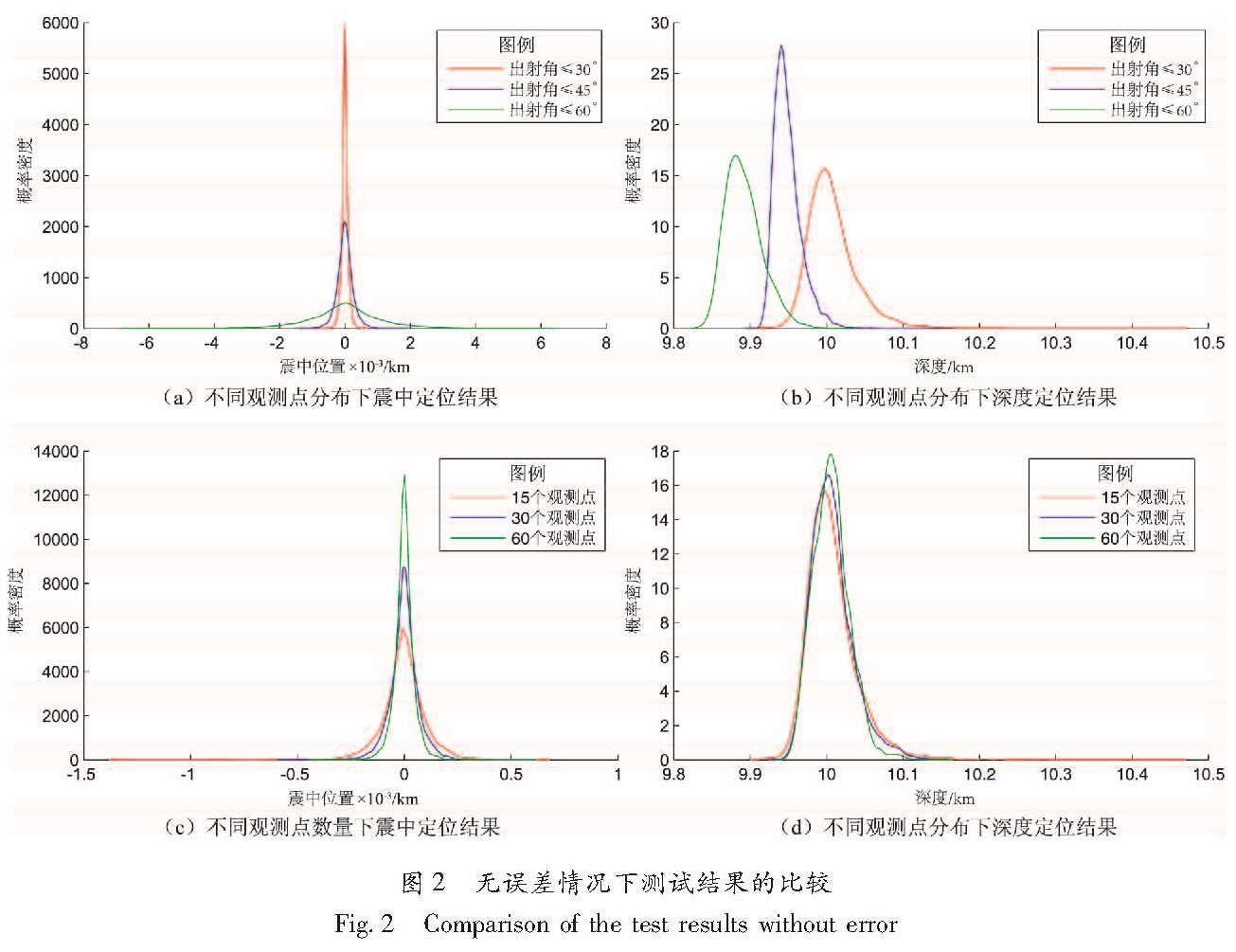
我们虚构了一个震中位置为0,震源深度为10 km的震源,并根据随机生成的参数生成了观测数据,最终反演得到了14万组定位结果。对这些结果进行比较,以观察不同的条件对于反演结果的影响。图2～4直观的表现了定位结果的差异。

图2展示的是在无误差情况下,观测点的数量和分布对于定位结果的影响。以图4可以看出,在无误差情况下,所有的结果都很接近虚拟的震源位置,尤其是震中的误差,被控制在数米之内; 而深度的误差也不超过0.5 km。观测点的数量和分布都会对震中的反演造成影响,不同的是,对于深度的确定,观测点的分布有着明显的影响,但观测点数量的影响却几乎可以忽略。综合起来看,观测点数量越多,分布的越密集,定位的效果就越好; 观测点的分布对于定位结果的影响比观测点数量更加显著。需要注意的是,图2b中,随着观测点的分布越来越稀疏,定位结果中深度

的概率峰值很明显的变小。形象的说,观测点的分布越稀疏,得到的震源深度越浅。同样,图2d显示,随着观测点数量的增加,概率密度峰值有轻微的右移,即深度的定位结果轻微的增大。

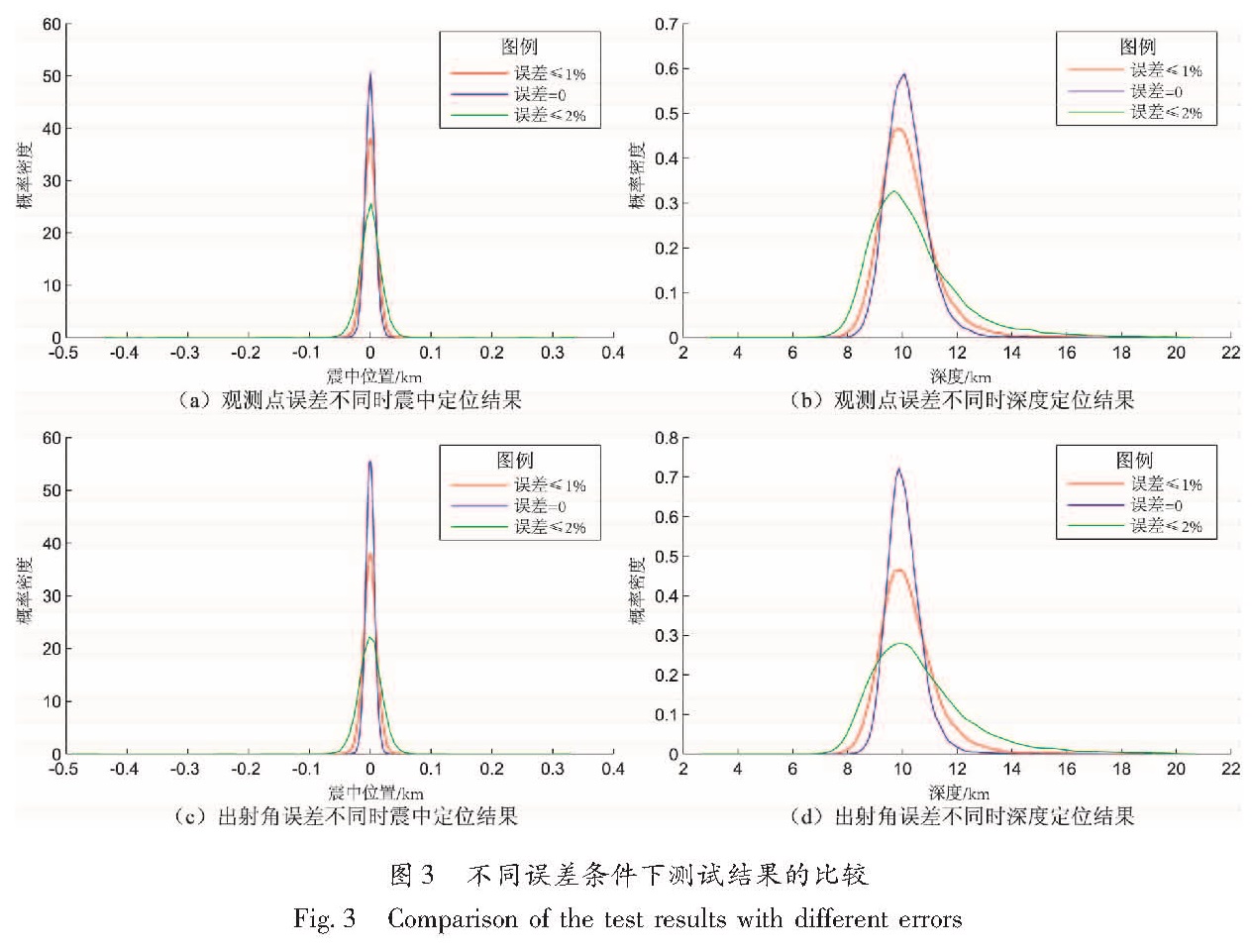
图3展示的是不同的误差对于定位结果的影响。在引入误差后,反演结果的概率密度曲线与图2相比,明显变得平缓,定位结果的误差水平也显著地增加。但是概率密度峰值对应的震中位置和深度并没有偏离虚拟震源的位置。绝大多数的震中位置的误差在50 m以内,深度的误差水平较高,但是也集中在2 km以内。综合起来看,Pg波偏振方向的误差和观测点坐标的误差对于定位结果有很明显的影响,并且都满足误差越小,定位越准确的规律。相比较而言,观测点坐标误差的影响要更大一些,但并不显著。同时,随着观测点坐标误差的增大,深度概率密度峰值也稍稍左移。并且,坐标误差的增大会导致定位深度的减小。在反演结果中,出现了极少数远远偏离虚拟震源位置的异常结果(主要是深度值异常,图中未显示),在后面的章节中,将对这种情况进行讨

图2 无误差情况下测试结果的比较
Fig.2 Comparison of the test results without error

图3 不同误差条件下测试结果的比较
Fig.3 Comparison of the test results with different errors

图4 特定误差情况下测试结果的比较
Fig.4 Comparation of the test results with a given error

论。从反演结果的误差水平上来看,各种误差对于定位结果的影响要远远大于观测点的分布和数量对结果的影响。

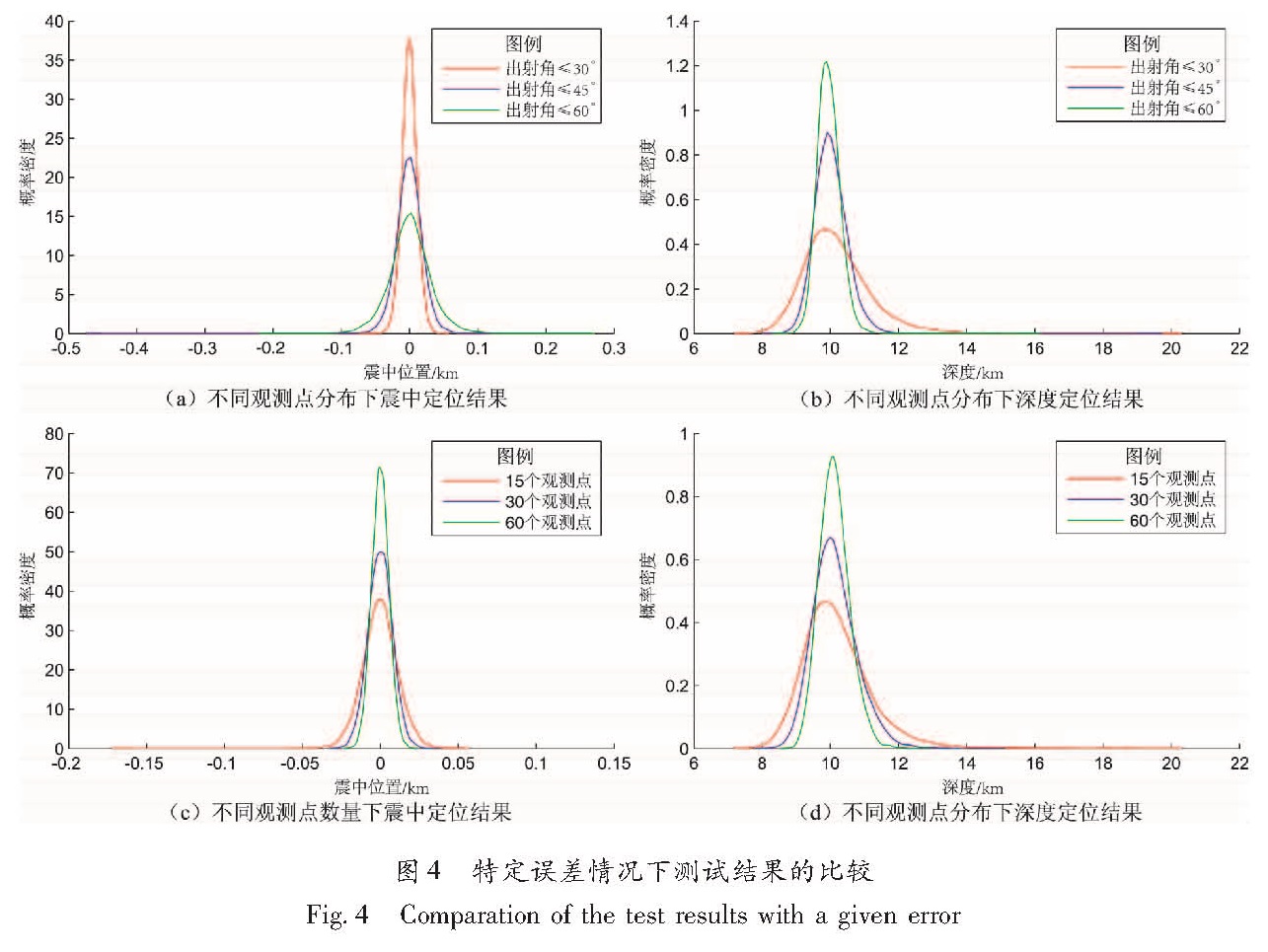
图4显示的是在一定误差水平下(Pg波偏振方向的正弦值误差≤ 1%,观测点的坐标误差≤ 1%)的定位结果。同图2相比,定位的精度极大的降低了,同时深度的概率密度峰值随观测点分布和数量的变化趋势都被一定程度的放大了。只是因为误差的影响太大,把这个变化给掩盖住了。同样的,反演结果中也出现了极少的远远偏离虚拟震源的异常点。

本文选取了2014年8月12日05:55:24.95发生在云南省大理州宾川县的2.8级地震对本方法进行检测。在震中20 km范围内,共有15个地震记录仪获取了本次地震的记录。定位的结果见表2。

通过表2可看出,本方法的定位结果与云南地震台网的定位结果很接近,震中位置相差小于2 km,震源深度相差也小于2 km。

表2 定位结果比较
Tab.2 Comparison on the locating result

图5 波速(归—化)对比
Fig.5 Comparation on wave velocity(normalization)

图5是本方法定位得到的波速比值r(r₁,r₂,…,r_n)与其它研究者结果(李聪,雷建设,2014)的比较。为了便于对比,都做了归一化处理。

通过对射线追踪方法的测试,我们认为该方法确实可以确定震源的空间位置。但是,由于需要获得比较“纯净的”Pg波偏振信息,因此,该方法不适用于远震定位。

该方法测试时,发现误差对于定位精确度的影响非常大,远远超过了观测点的分布和数量对于定位精确度的影响。总的来说,降低误差水平,提高观测点的数量和密度都能够提升定位结果的精确度; 反之亦然。另外,观测点的密度降低和坐标误差的增大会使深度的定位结果变小; 而观测点数量的增加会导致深度的结果变大。

和深度不同,震中的最大概然值并没有随着其它条件的变化而变化,造成两者间区别的原因可能是观测点在不同方向上的分布不同。由于出射角的生成是随机的,因此,观测点在水平方向上的分布应该是比较均匀的,不会产生大部分的观测点都位于震中某一边的情况; 而在竖直方向上,所有观测点的值都为0,全部位于震源的上方。在有误差存在的反演结果中,出现了极少数的远远偏离震源的异常值。对于这些异常的产生,我们推测有2种可能的原因:随机误差的不均匀; 反演程序自身的缺陷。对于震中距不同的观测点来说,其在反演过程中的权重是不一样的。这一点可以通过图2a、b和图4a、b看出。因此当某个权重较大的观测点获得了较大的误差后,就会对定位过程产生严重的影响。另一方面,如果收敛条件的设定不合适,也可能会导致反演程序给出局部极小值点。

从测试中可以看出,震中定位的精确度是很高的。因此,将射线追踪法(或者其它定位方法)得到的震中作为先验条件,再对震源深度进行单独定位,也许会得到更加可靠的结果。另外,我们注意到,在反演的过程中,我们将地表和震源中间的介质分层,并得到了相应的波速比值r(r₁,r₂,…,r_n)。利用这组数值,我们可以通过线性反演获得“发震时刻”和各层介质的“波速”。但是,由于我们并不清楚这组波速比值是否对应着真实的速度结构,因此,我们也不知道通过该方法得到的“发震时刻”和“波速是否是正确的。

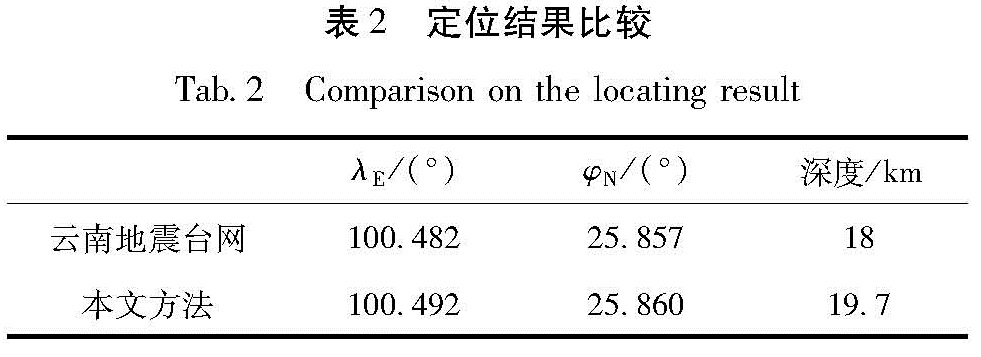
通过一例真实地震的检验,发现本定位方法的结果和其他研究者的结果较为接近,因此,我们认为射线追踪方法可以用于真实地震的定位。

今后,我们将从5个方面展开工作:改进程序和算法,降低异常结果的产生; 提高定位结果,尤其是深度定位结果的精确度; 发震时刻的定位; 复杂介质条件下,射线追踪法的应用; 用更多真实的地震数据来检测该方法,并最终将其应用于实际的地震定位中。

在本文的写作和修改过程中,杨润海高工提供了地震资料和指导,颜其中研究员对本文提出了建议,我的硕士导师倪四道教授和崔建文研究员也给予了指导和帮助,在此一并致谢。同时,也感谢审稿专家的修改意见和编辑的辛勤工作。