基金项目:黑龙江省地震局一般项目(201805)和地震行业科研专项(201508009)联合资助.
(1.黑龙江省地震局,黑龙江 哈尔滨 150090; 2.黑龙江省鹤岗地震台,黑龙江 鹤岗 154101; 3.中国地震局地质研究所 地震动力学国家重点实验室,北京 100029)
(1.Heilongjiang Earthquake Agency,Harbin 150090,Heilongjiang,China)(2.Hegang Seismic Station of Heilongjiang Provice,Hegang 154101,Heilongjiang,China)(3.State Key Laboratory of Earthquake Dynamics,Institute of Geology,China Earthquake Administration,Beijing 100029,China)
备注
基金项目:黑龙江省地震局一般项目(201805)和地震行业科研专项(201508009)联合资助.
通过计算GPS时间序列共模误差,对大华北地区(华北和东北)不同尺度的共模误差进行分析和讨论,结果表明:计算共模误差时可采用Stacking与 PCA方法相结合的方法,空间上需对测站进行细致挑选,区域面积在覆盖测站的条件下应尽可能小; 扣除随机噪声试验说明并非用任意噪声序列都能起到共模误差滤波的作用; 东北大尺度区域含有较多的框架误差成份,京津冀小尺度区域含有的共模误差成分比东北大尺度区域更多。
Through computing GPS time series Common Mode Error(CME),we analyze and discuss the CME of different scales in North China region.The results show that the station should be carefully selected when calculating the CME.The area should be as small as possible under the conditions of meeting the requirements of the full coverage of the stations.The method of Stacking and PCA can be used in the calculation method.Deducting the random noise test shows that it is not possible to use any noise sequence to play the role of CME.Large scale regions contain more frame error components.The small scale region of Jingjinji contains more CME components than the northeast large scale region.
引言
连续GPS坐标时间序列中包含某种时空相关的误差,表现为测站时间序列之间存在高度相关性,称之为共模误差,其产生主要由大区域范围内由卫星轨道和卫星天线相位中心误差等大尺度因素所导致,局域范围内可能与陆地水储量等小区域因素变化有关(盛传贞等,2014; 田云锋等,2009,2010; 苏丽娜等,2014; 谢树明等,2014; 杨博等,2014)。
共模误差的存在会影响GPS坐标时间序列中微小地壳形变信号识别(伍吉仓等,2008; 杨博等,2010a,b; 唐江森等,2016; 胡守超等,2009),导致对地震前兆信息的误判,所以在GPS时间序列分析时需要对区域共模误差进行扣除。Tian和Shen(2016)研究得出共模位置偏移通常是通过统计方法来估计的,不仅包括误差而且还存在信号,他提出使用共模误差成分(Common-Mode Componet,简称CMC)这一概念,对于构造运动研究,大尺度CMC等效于传统的共模误差(CME)。目前关于共模误差的研究主要集中在计算方法和频谱特征分析上,而对于不同空间尺度分区域实测数据共模误差剔除及相互联系研究较少。
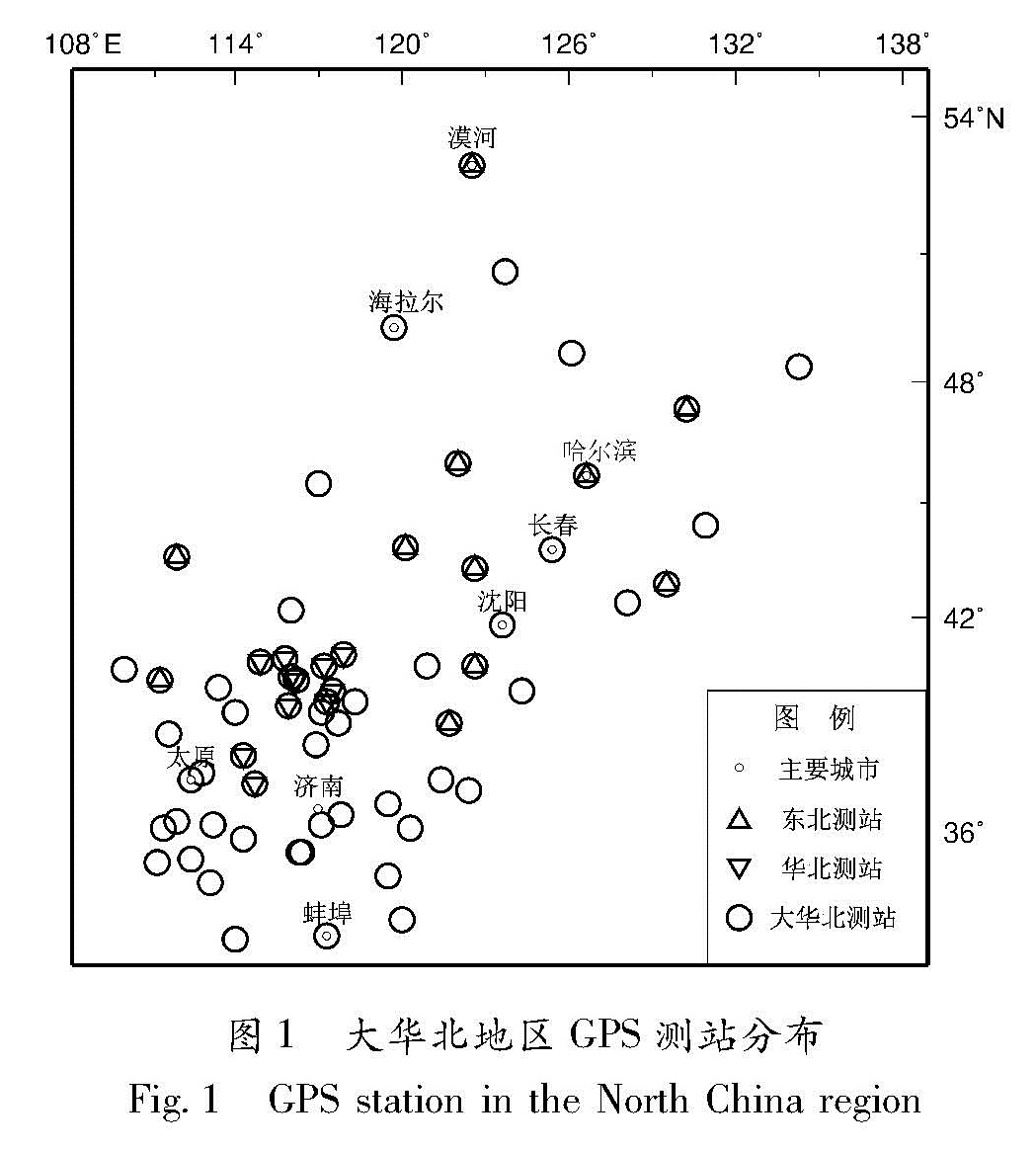
本文在已有研究的基础上,结合不同共模误差计算方法,以大华北地区为例,分区域计算共模误差,分析不同尺度区域共模误差相互关系。本文所指的大华北地区(108°~136°E,33°~54°N)包括北京、天津、河北、黑龙江、吉林、辽宁、山东、山西的全部以及内蒙古、河南、安徽、江苏部分地区。
1 数据处理及研究方法
计算共模误差应以准确的GPS时间序列结果
为基础,所以首先必须对GPS数据进行可靠的处理。本文采用美国航空航天局(NASA)喷气推进实验室(JPL)的GIPSY/OASIS(Version 6.0)软件和PPP模式对每日数据进行严密处理,获得单日松弛约束解。然后采用JPL的联合平差软件QOCA(Dong et al,1998),对所有站点的单日松弛约束解严密平差,获得包括北京、天津、河北、山东等地区共计64个连续GPS观测站(图1)的原始坐标变化时间序列(因篇幅所限,仅给出鹤岗站结果)。在此基础上,采用以下处理原则,对GPS时间序列进行预处理:(1)首先定义超过观测数据平均误差的20倍为未能解算的数据(通常的原因是单日的有效观测时间太短)、5倍为粗差观测值、3倍为异常观测量,并对其进行扣除。对同震位错和人为更换引起的天线变化,取变化前、后若干天的加权平均值,作为天线的偏移量,进行统一校正;(2)在去除时间序列的各种偏移“阶跃”后,通过加权线性回归计算趋势项。去趋势后以3倍标准偏差作为判别标准,剔除残差时间序列的“非正常误差”(粗差),最后得到“干净”时间序列和残差时间序列。图2中鹤岗站预处理前后时间序列对比,可以看出预处理可以将时间序列阶跃和突跳有效剔除。
计算共模误差之前采用以下模型对GPS位移时间序列进行拟合:
y(ti)=a+bti+csin(2πti)+dcos(2πti)+
esin(4πti)+fcos(4πti)+∑ngj=1gjH(ti-Tgi)+
∑nhj=1hjH(ti-Thi)ti +vi(1)
式中:a为初始位置; b为速率; c,d,e和f为周年、半年周期项系数; g为由同震或天线位置变动引起的阶跃,已在前面数据预处理中剔除; vi为误差; ti为时间。式(1)采用最小二乘法求解。由测站每个坐标分量观测值时间序列去除趋势项和周期项得到的残差坐标时间序列作为计算共模误差的基础。
利用实测数据计算共模误差往往存在许多实际困难,如GPS站点数据的不连续、某时段可能存在源于天线墩不稳定或周边环境的干扰引起的单站误差等,这些因素对计算共模误差准确度影响较大,虽然有一些方法可以抑制噪声,但本文更倾向于这样的站点不参与共模误差的计算(相当于KLE方法作用)。同时,共模误差应包括区域共同误差和地壳运动信息,在计算共模误差时应挑选可反映区域共同细节变化的站点,如果不确定的话,应尽可能用足够多的站点来代替,前提是把相对其它有明显差别的站点剔除,挑选的站点应该至少满足最大的连续性及最可能的共同变化,这样得到的共模误差才能最大程度的代表区域共同变化。基于以上筛选原则,本文在华北和东北地区各选取了11个站,站点尽可能做到最大覆盖,同时有一定的重复区域(图1)。
目前计算共模误差常用的方法有区域堆栈方法(Stacking)、主分量分析方法(PCA)、和Karhunen-Loeve方法(KLE)(Wdowinski et al,1997; Dong et al,2006)。Stacking方法对空间分布均匀、较小的GPS网有明显的效果,但无法揭示共模误差的空间分布; PCA方法在分离共模误差的同时,可以得到共模误差准确的空间响应,但对于含有较强本地影响的GPS网,无法保证正确分离出共模误差; KLE方法可以抑制本地噪声影响,从含有较强本地影响的时间序列中提取共模误差,但得不到准确的空间响应(杨博,2010a)。
为了选取最好的计算方法,笔者使用这3种方法进行实际计算,发现如果采用PCA(或KLE)方法,若数据中存在一个空值即会导致所有测站该历元值为空,观测数据量将大大减小。而在对观测数据进行过筛选的基础上,即使一个测站缺测,使用Stacking方法也会得到较理想共模误差。因此,首先采用Stacking方法对大华北地区测站分离共模误差,然后用得到的共模误差对观测数据进行补值,最后用PCA方法得到兼具Stacking和PCA方法的优点的共模误差。
2 华北地区小区域尺度共模误差
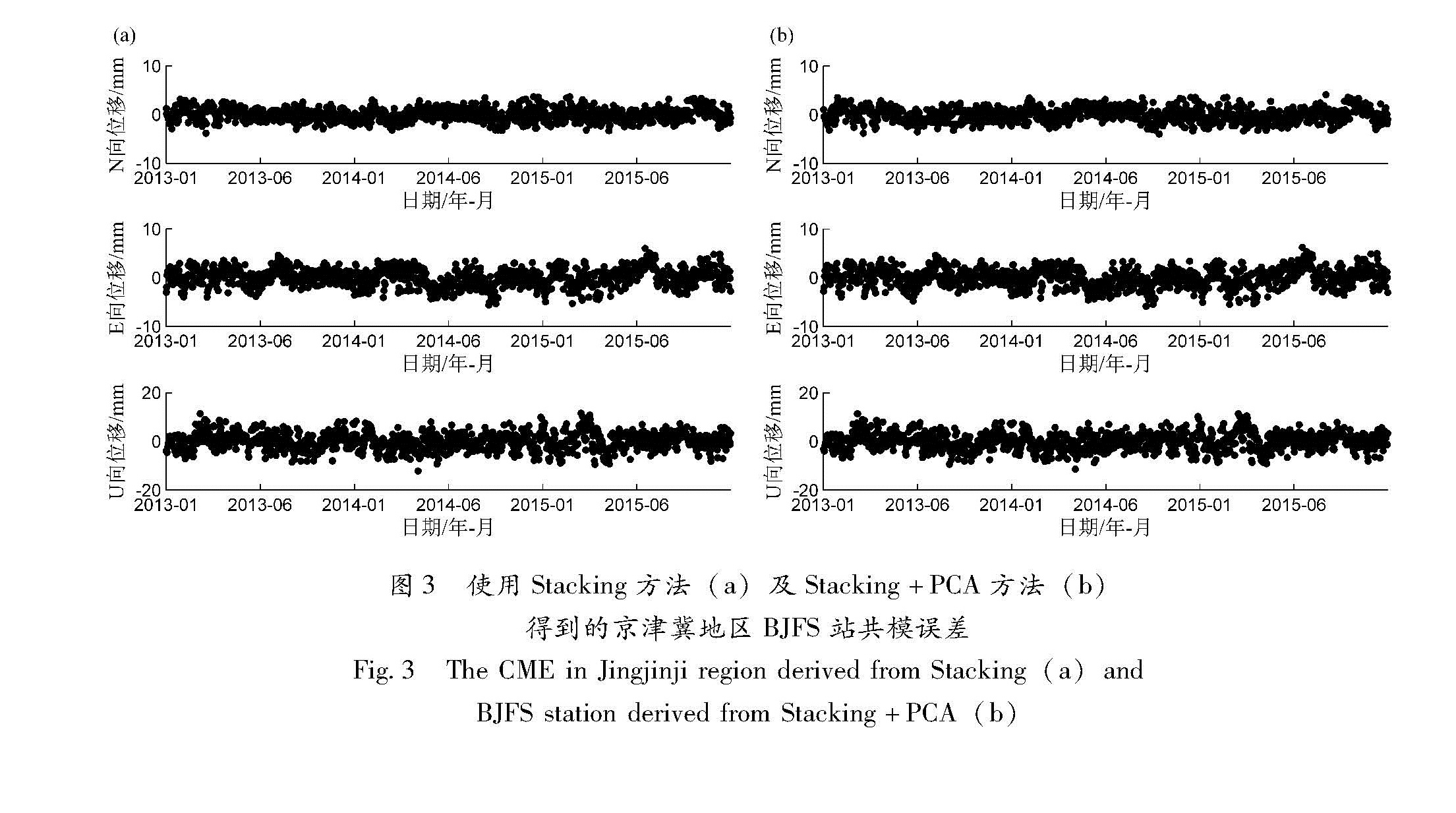
分别采用Stacking方法和Stacking+PCA方法计算华北地区小区域尺度(以下简称京津冀地区)共模误差,计算结果如图3所示。从图中可以看出,
采用Stacking 和Stacking+PCA结合的方法均能得到很好的区域共模误差,两次所得共模误差时序曲线基本一致,而Stacking+PCA方法同时能反映各站共模误差的空间分布特征。
为了着重比较分析不同空间尺度分区域共模误差的特点和相互关系,以Stacking方法为例进行说明(图3)。图3a中共模误差时间序列振幅较小,水平方向最大振幅大部分在5 mm以内,垂直方向在10 mm以内。以标准差表示共模误差的离散度,标准差可以客观地表示1组数据的离散程度。计算公式如下:
α=((∑ni=1(Xi-X^-)2)/(n-1))1/2(2)
式中:Xi为N,E,U向第i个位移值; X^-为位移平均值; n为变量个数。
京津冀地区N,E,U向的共模误差离散度分别为1.51 mm,2.00 mm和4.88 mm,可以看出小区域共模误差水平向影响较小、垂直向略高。
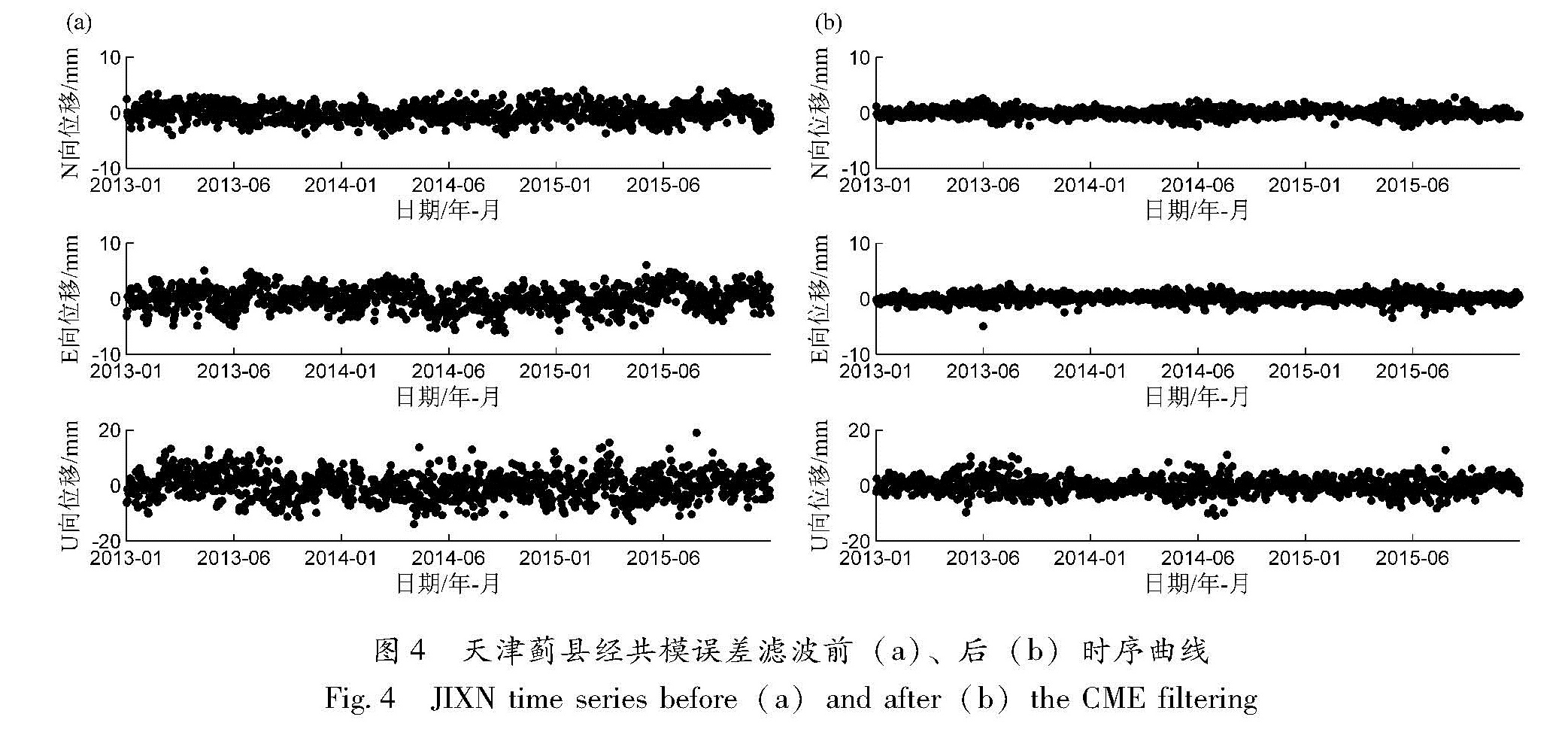
共模误差反映的是测站共同运动情况,共模误差时序曲线转折变化影响着测站运动差异的判断。经共模误差滤波后(图4b),测站时序曲线离散度明显减小。实际观测也发现台基及区域应力环境较为稳定的测站所显现的地壳运动基本上是
图3 使用Stacking方法(a)及Stacking+PCA方法(b)得到的京津冀地区BJFS站共模误差
Fig.3 The CME in Jingjinji region derived from Stacking(a)and BJFS station derived from Stacking+PCA(b)表1 京津冀地区经共模误差滤波前、后时间序列离散度及变化幅度
Tab.1 Time series dispersion and variation amplitude in Jingjinji region before and after the CME filtering线性的,也就是说,正常情况下测站坐标时间序列是噪声叠加在线性变化或有规律变化上(Dong et al,1998),时序曲线离散度越小描述区域单站运动越清晰,计算运动速率及区域速度场越准确。
从京津冀地区经共模误差滤波前、后离散度数值对比可以看出(表1):滤波后时序曲线离散度明显减小,11个测站的离散度N向平均值由1.51降为0.84,降幅为44.49%; E向由2.00降为0.87,降幅为56.47%; U向由4.88降为3.28,降幅为32.66%。因此,共模误差对于曲线的描述运动清晰程度起较大的作用。经共模误差滤波后的时间序列,不仅有效剔除了测站公共运动,也凸显了单台构造运动特征,同时也有助于发现单台数据异常,做好数据异常跟踪工作。
3 东北地区大区域尺度共模误差
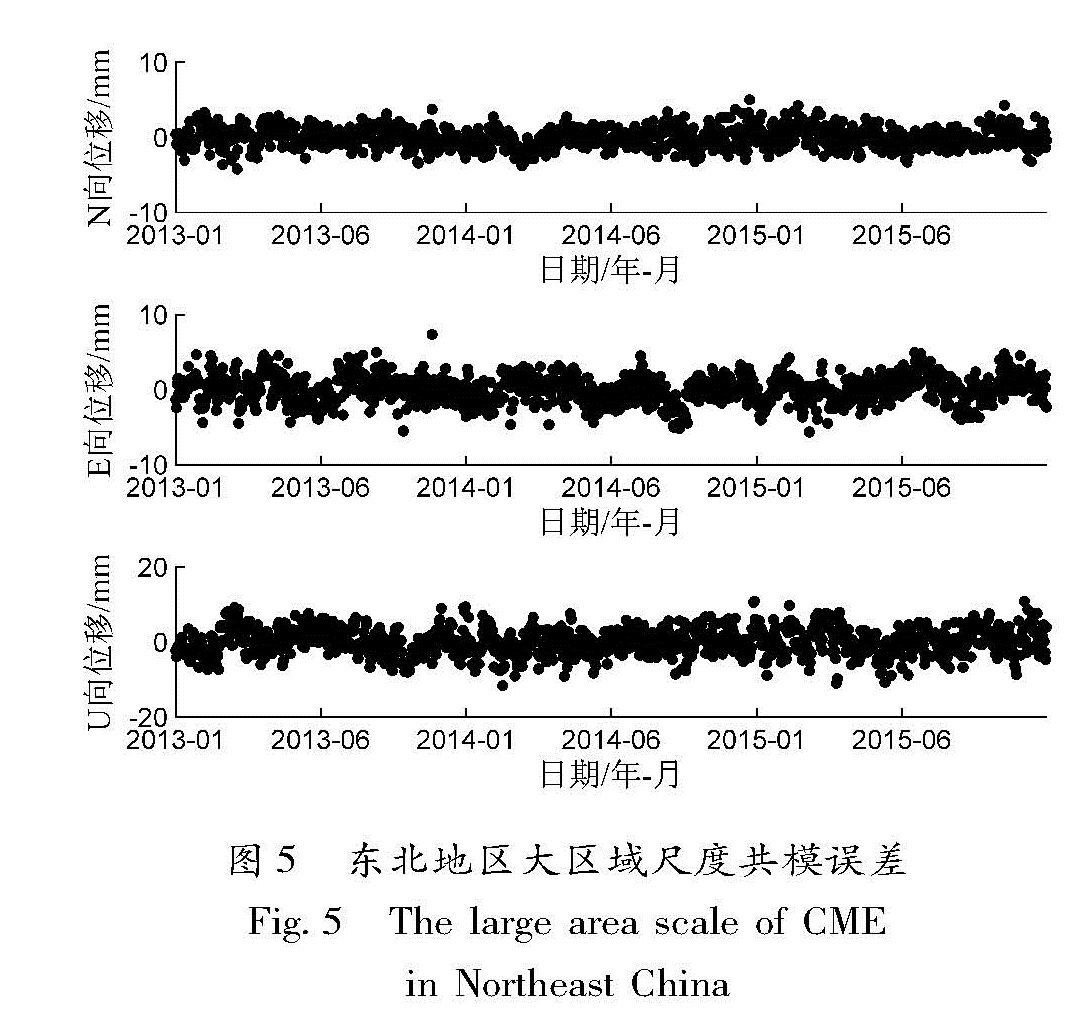
东北地区范围辽阔,地壳运动稳定,是否同样也受共模误差的影响?影响程度是否与华北地区小区域尺度等同?使用Stacking方法对东北地区平均间隔400 km的11个GPS连续站,计算共模误差,结果如图5所示。
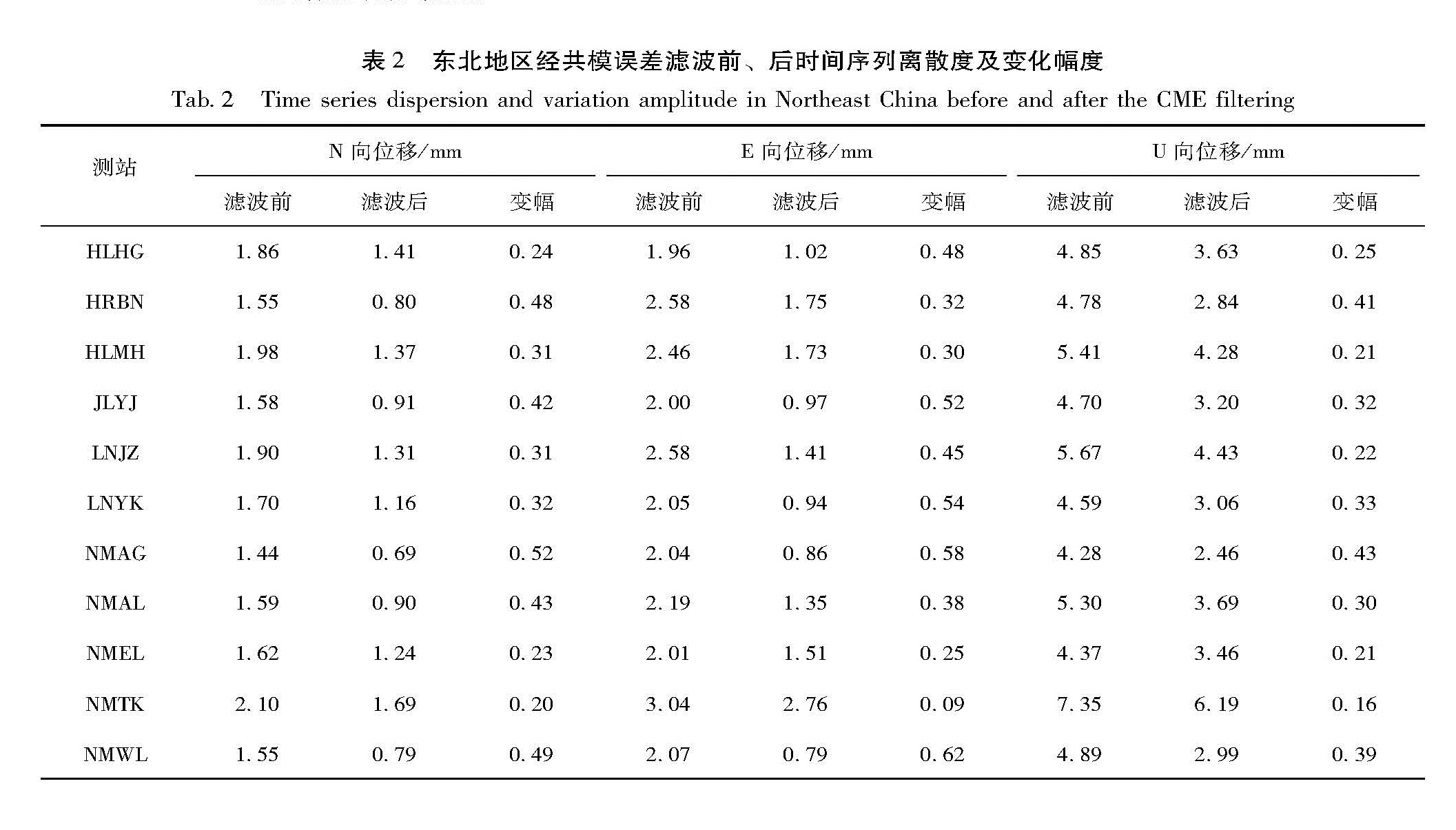
对东北地区经共模误差滤波前、后离散度数值对比可以看出(表2):11个站的离散度N向平均值由1.71降为1.11,降幅为35.90%; E向平均值由2.27降为1.37,降幅为41.18%; U向平均值由5.10降为3.65,降幅为29.36%。东北地区大区域尺度经共模误差滤波后,离散度不如京
津冀小区域降幅大,说明小区域滤除共模误差的作用更明显。因此在满足覆盖待求测站的前提下,区域面积选取应尽可能小。4 讨论
许多学者研究表明GPS观测噪声包含白噪声和闪烁噪声(沈正康,2009; 黄立人,2006; 黄立人,符养,2007),少数测站还包含随机游走噪声,共模误差也具备上述噪声的特点。如果将时间序列扣除随机获取的噪声序列是否也能消弱噪声、减小离散度和扣除共模误差能否达到相同的效果?基于上述考虑,本文试验如下:将京津冀地区共模误差最后1 d值拷贝为第一个值,整体向后平移1 d,看作随机产生的噪声序列,再用天津蓟县(JIXN)站GPS时间序列扣除该随机噪声时间序列,扣除前后时间序列如图6所示。由图6可见,扣除随机噪声时间序列后时序曲线呈现明显的噪声特征,原有曲线转折变化不复存在,而且N,E,U向离散度分别由1.47,2.00,4.82变为1.65,1.98,4.45,没有减小。该结果说明并非任意噪声序列都能起到共模误差的作用,同时也说明本文计算共模误差的方法是正确的。
表2 东北地区经共模误差滤波前、后时间序列离散度及变化幅度
Tab.2 Time series dispersion and variation amplitude in Northeast China before and after the CME filtering大空间尺度如东北区域的共模误差中是否含有参考框架成份呢?因为框架成份是所有测站所共有的,如果有的话,那么用京津冀地区小区域尺度时序曲线扣除东北地区大区域尺度共模误差离散度也应该减小,计算结果如图7所示。
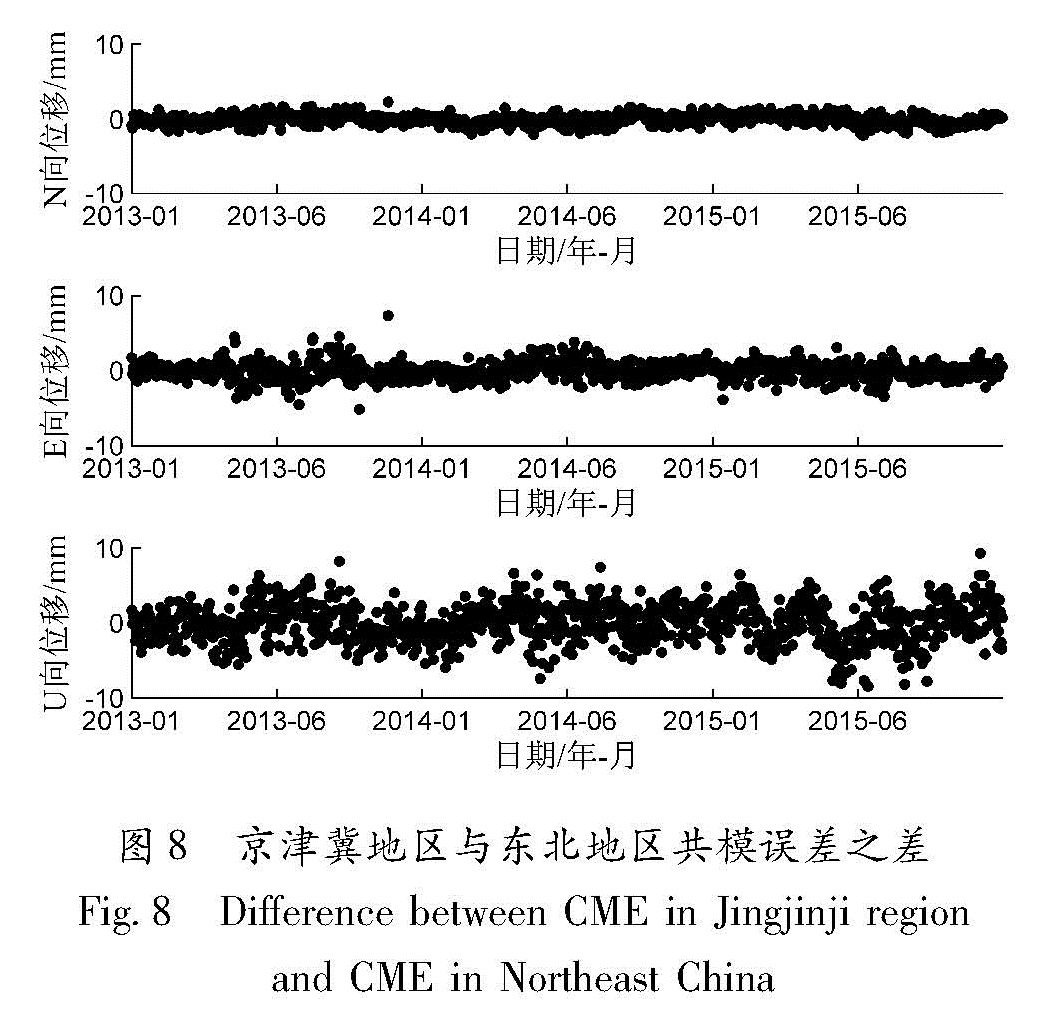
从图7可看出,京津冀地区时序曲线扣除东北共模误差后,离散度仍减小,但减小幅度比扣除京津冀共模误差小。说明东北共模误差含有参考框架成分,这部分信息也是京津冀地区共有的。因此,将2个区域共模误差作差,结果如图8所示。从图8可以看出,2个区域共模误差所含公共参考框架成分比较多,特别是水平方向,但仍然存在一些差别。因为小区域滤波效果好于大区域尺度,也证明了小区域尺度所含共模误差
图7 天津蓟县经京津冀共模误差(a)及东北共模误差(b)滤波后时序曲线
Fig.7 JIXN time series filted by the CMEs of Jingjinji(a)and Northeast China(b)
成份更多。同样认为在实际剔除共模误差时,应在把区域内各站包括进去的前提下,覆盖面积尽可能的小。5 结论
通过对大华北地区GPS时间序列共模误差的计算和分析,得到以下结论:
(1)计算共模误差时应挑选可反映区域共同细节变化的站点,如果不确定的话,尽可能用足够多的站点来代替,前提是把相对其它站点有明显差别的站点剔除,挑选的站点应该至少满足:最大的连续性及最可能的共同变化,这样得到的共模误差才能最大程度代表区域共同变化。
(2)计算方法上可采用Stacking+ PCA方法相结合的方法,得到兼具Stacking和PCA方法优点的共模误差。
(3)扣除随机噪声试验说明并非用任意噪声序列都能起到共模误差滤波的作用。
(4)大空间尺度共模误差含较多的参考框架成份,框架成份也是包括小区域所共有的。相比大区域,小区域所含的共模误差成份更多,滤除共模误差的作用更明显,因此在满足覆盖待求测站的前提下,区域面积选取应尽可能小。
国家重大科学工程“中国大陆构造环境监测网络”为本文提供GNSS观测数据; 匿名审稿专家和编辑老师针对研究方法及文章写作提出了非常宝贵的修改意见和建议,在此一并表示感谢!
- 胡守超,伍吉仓,孙亚峰.2009.区域GPS网三种时空滤波方法的比较[J].大地测量与地球动力学,29(3):95-99.
- 黄立人,符养.2007.GPS连续观测站的噪声分析[J].地震学报,29(2):197-202.
- 黄立人.2006.GPS基准站坐标分量时间序列的噪声特征分析[J].大地测量与地球动力学,26(2):31-38.
- 沈正康.2009.GPS坐标时间序列中非构造噪声的剔除方法研究进展[J].地震学报,31(1):68-81.
- 盛传贞,甘卫军,梁诗明,等.2014.滇西地区GPS时间序列中陆地水在和形变干扰的GRACE分辨与剔除[J].地球物理学报,57(1):42-52.
- 苏丽娜,丁晓光,张彦芬,等.2014.陕西连续GPS基准站坐标时间序列分析[J].大地测量与地球动力学,34(5):106-109.
- 唐江森,曲国庆,袁兴明,等.2016.区域GPS网共模误差的提取与分析[J].山东理工大学学报(自然科学版),30(6):48-52.
- 沈正康.2009.GPS坐标时间序列中非构造噪声的剔除方法研究进展[J].地震学报,31(1):68-81.
- 田云锋,沈正康,李鹏.2010.连续GPS观测中的相关噪声分析[J].地震学报,32(6):696-704.
- 伍吉仓,孙亚锋,刘朝功,等.2008.多连续GPS站坐标序列共性误差的提取与形变分析[J].大地测量与地球动力学,28(4):97-101.
- 谢树明,潘鹏飞,周晓慧,等.2014.GPS坐标时间序列共模误差空间特性分析[J].地理空间信息,12(4):44-54.
- 杨博,占伟,刘志广,等.2014.多核函数法对GNSS大空间域共模误差的识别[J].测绘科学技术学报,31(2):127-132.
- 杨博,张风霜,韩月萍.2010a.天津地区连续GNSS时序观测值共模误差识别[J].测绘科学技术学报,27(5):319-323.
- 杨博,张风霜,韩月萍.2010b.GPS连续站水平分量时间序列共模误差[J].大地测量与地球动力学,30(3):100-104.
- Dong D,Fang P,Bock Y,et al.2006.Spationtemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis[J].J Geophys Res,111(B3):B03405-B03405.
- Dong D,Hering T A,King R W.1998.Estimating regional deformation from a combination of space and terrestrial geodetic data[J].J Geophys Res,72(4):200-214.
- Tian Y F,Shen Z K.2016.Extracting the regional common-mode component of GPS stati-ion position time series from dense continuous network[J].Jouranl of Geophysical Research:Solid Research:Solid Earth,121(2):1080-1096.
- Wdowinski S Y,Bock Y,Zhang J,et al.1997.Southern California permanent GPS geodetic array:Spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 landers earthquake[J].J Geophys Res,102(B8):18057-18070.