基金项目:国家自然科学基金(51508527,51378477)、国家科技支撑计划(2015BAK18B01)和中国地震局地球物理研究所基本科研业务费专项(DQJB15C05)共同资助.
(Institute of Geophysics,China Earthquake Administration,Beijing 100081,China)
seismic ground motion parameters; intensity; damage ratio matrix; fragility curve; the maximum likelihood estimation method
备注
基金项目:国家自然科学基金(51508527,51378477)、国家科技支撑计划(2015BAK18B01)和中国地震局地球物理研究所基本科研业务费专项(DQJB15C05)共同资助.
基于房屋结构地震反应基本服从对数正态分布的特点,提出了一种房屋震害矩阵曲线化分析方法,将已有的房屋易损性矩阵或实际震害统计的破坏比结果转化为双参数易损性曲线。首先将不同烈度下房屋处于不同破坏状态的概率转化为超越概率,再结合烈度与地震动参数之间的对应关系,采用最大似然估计方法计算超越不同极限状态易损性曲线的均值和标准差,最后得到不同地震动参数对应的房屋结构易损性曲线。以四川省房屋震害矩阵为例,给出了各类房屋结构的地震易损性曲线特征参数。
Based on the earthquake response of structure subjected to lognormal distribution,we propose a method for damage probability matrices to be presented by fragility curves,which transforms the damage ratio of existing building or actual earthquake damage statistics into the fragility curves. First of all,we transform the damage probability of the buildings in different intensity levels into exceed damage probability. Secondly,combined with the corresponding relationship between intensity and ground motion parameters,we calculate the mean values and standard deviation values of fragility functions in different damage limit states by the maximum likelihood estimation method. Finally,we get structures fragility curves corresponding to different ground motion parameters. Taking the structure damage matrix of Sichuan Province as an example,we give the seismic fragility curve parameters of various types of structure. It is verified that this method has a high reliability and accuracy and can provide the basis for building seismic risk assessment and estimation of earthquake insurance.
引言
我国是世界上陆地地震灾害最严重的国家之一,特别是随着经济建设和城市化进程的不断加快,地震灾害潜在风险水平不断提高。易损性分析作为灾害风险分析的3个主要部分(地震危险性分析、承灾体的易损性分析、灾情损失评估)之一,其核心是建立建筑结构出现或超越各种破坏状态的概率与地震强度之间的关系。开展建筑结构地震易损性分析对于地震破坏和损失预测以及减轻地震灾害具有十分重要的意义。
在实际地震现场和震害预测的工作中,研究人员积累了大量基于烈度的建筑结构震害经验关系,即用烈度-震害程度的比例或概率构成的易损性矩阵,然而烈度的获得是基于人的感觉、器物反应、房屋为主的工程结构破坏、地表破坏等4类宏观现象来评定(胡聿贤,2006; 中国地震烈度表,GB/T 17742—2008; 明小娜等,2017)。这也意味着随着我国建筑抗震设防水平的提高,不同时期烈度本身的度量尺度也会发生变化,所以基于烈度的易损性矩阵具有较大的不确定性(Lagomarsino,Cattari,2014)。然而以往大多数震害预测中关于房屋建筑易损性的评估,都是基于烈度进行,即表示结构在不同烈度下出现各破坏状态的概率(韩淼等,2009)。为了准确预测建筑结构的抗震性能,更好地进行结构抗震设计,完成对现有建筑物的加固和维修,加快地震保险在全国范围内的推行,基于烈度的易损性矩阵很难满足实际需要,特别是对于土木结构、砖石结构等简易房屋,难以通过结构模拟分析获取其易损性曲线,如何完善现有的易损性矩阵,并将基于烈度的易损性矩阵转化为更合理的基于地震动参数的易损性矩阵显得尤为重要(胡少卿等,2007; 刘如山等,2009; 李静等,2012; 马玉宏等,2015)。
本文采用最大似然估计的曲线方法对震害资料进行分析。选取PGA作为地震动参数,根据烈度与地震动参数之间的对应关系,将结构基于烈度的不同破坏状态的概率矩阵转化为基于PGA的不同破坏状态的概率矩阵,得到连续的基于地震动参数的易损性曲线。
1 易损性矩阵曲线化方法
地震易损性是指结构在不同地震作用下,出现各种破坏状态的条件概率,它从概率的角度定量表征结构的抗震能力,表达式为:
F(IM=x)=P(IM≥IMC/IM=x)
=P(IMC≤x)(1)
式中:IM为地震动强度指标; IMC是结构物达到破坏状态时对应的地震动参数; F(IM)为易损性函数。
建筑结构易损性主要通过地震易损性曲线和震害矩阵来表示。一般易损性曲线横坐标为地震的强度指标,如烈度、峰值加速度、峰值速度、地震动反应谱值等,纵坐标为达到不同破坏等级的超越概率。易损性曲线的获得可以通过经验法(Colombi et al,2008)、解析法(Lagomarsino,Cattari,2014)及混合法(Aldemir et al,2013)。在易损性的研究进程中对易损性函数的选用,不同学者提出了不同的数学模型,如:逻辑回归函数(Singhal,Kiremidjian,1998)、威尔逊分布函数(Shinozuka et al,2007)、对数正态分布函数(Shinozuka et al,2000; Yamazaki et al,2000)等,其中对数正态分布最为常用。
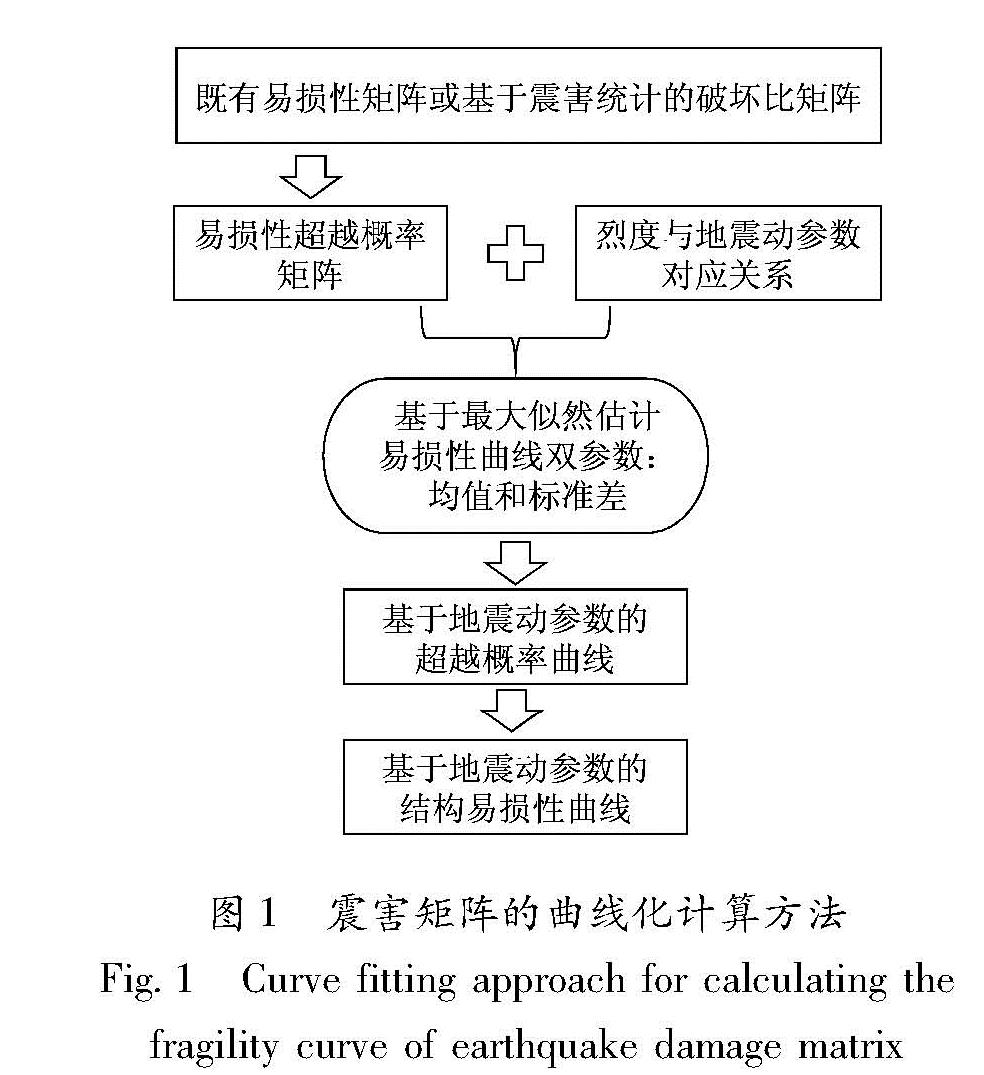
易损性曲线的拟合方法有很多种,如多项式拟合、最小二乘法拟合、最大似然估计法拟合等(Shinozuka et al,2000; Baker,2013; 陈力波等,2012; 吴子燕等,2014; 林庆利等,2017)。本文采用最大似然估计法,通过MATLAB程序做具体计算和绘制易损性曲线,获取基于地震动参数的易损性曲线的具体流程,如图1所示。
图1 震害矩阵的曲线化计算方法
Fig.1 Curve fitting approach for calculating the fragility curve of earthquake damage matrix1.1 建筑物破坏等级分类建筑物破坏等级通常可分为5类(GB/T 24335—2009):DSk(k=0,1,…,4)分别表示基本完好、轻微破坏、中等破坏、严重破坏、毁坏5种破坏状态。LSs(s=1,2,3,4)为5种破坏状态之间的阈值,分别代表“轻微破坏”“中等破坏”“严重破坏”“毁坏”4种破坏状态的极限值,如图 2所示。
1.2 烈度与地震动参数对应关系地震烈度是地震引起的地面震动及其影响的强弱程度。鉴于早期监测条件的限制,详细的强震记录很难获得,但是通过烈度评定,地震工作者积累了丰富的宏观烈度资料。胡聿贤和张敏政(1984)提出了缺乏强震观测资料地区地震动参数的估算方法; 田启文等(1986)进行了根据烈度资料估算我国地震动参数衰减规律的一系列研究; 特别是《中国地震烈度表》(GB/T 17742—2008)作为我国地震烈度的评定标准,给出了烈度与峰值加速度(PGA)和峰值速度(PGV)之间的对
表1 地震烈度与峰值加速度PGA和峰值速度PGV的对应关系
Tab.1 The correspondence between seismic intensity and peak ground acceleration and peak ground velocity应关系。本文采用《中国地震烈度表》(GB/T 17742—2008)给出的烈度与地震动参数之间的对应值,从表1中可以看出,每一个烈度对应的PGA和PGV。
1.3 基于最大似然估计法确定易损性双参数在易损性研究的进程中,对数正态分布数学模型作为易损性的概率模型已经被验证是一种成熟、理想的模型,本文也采用对数累计正态分布函数作为易损性函数。易损性函数定义为:
F(IM=x)=P(C〖JB<1|〗IM=x)=Φ[(ln(x/θ))/β](2)
式中:P(C〖JB<1|〗IM=x)是地震动强度达到IM=x时,结构物到达某一极限状态的概率; Φ是标准累积正态分布函数; θ是易损性函数的中位数,β为lnIM的标准差。
对于超越破坏状态的结构,由式(2)定义的易损性函数,可以得到在IM=xi处的似然函数的密度函数:
L=φ[(ln(x/θ))/β](3)
相应的,对于未超越破坏状态的结构,在IM=xi处的似然函数的密度函数为:
L=1-φ[(ln(x/θ))/β](4)
根据不同的破坏状态有不同的中位数θ和对数标准差β,定义似然函数为:
L=∏Ni=1φ[(ln((xi)/θ))/β]ti×〖JB<4{〗1-φ[(ln((xi)/θ))/β]〖JB>4}〗1-ti(5)
式中:N为统计结构总数; xi表示第i栋结构对应的峰值加速度; ti为伯努利事件,如果达到破坏状态,ti=1,否则,ti=0。
双参数θ和β计算公式为:
(lnL)/(θ)=(lnL)/(β)=0(6)
2 震害矩阵曲线化实例
2.1 震害资料的收集和统计地震现场作为大的原型实验场,工程结构的真实震害经验是地震工程学发展的重要支柱,人类如何抗御地震灾害的认识很大程度也来源于此(温增平等,2009)。四川省地质构造复杂,地震活动频繁,房屋结构类型多样,历史上发生过多次7级以上特大地震,特别是2008年汶川8.0级地震、2013年芦山7.0级地震造成了严重的经济损失和人员伤亡。孙柏涛等(2014)采用不同分级和分区域的方法研究了南北地震带各类房屋建筑的分布特征和抗震能力,以四川省为例,将其分为:I区,西部地区; II区,中北部地区; III区,中南部地区。结合6个地级市204个调查点的23 964栋房屋建筑调查结果和汶川地震等历史震害经验对其房屋建筑进行调查,给出了分区域各类结构房屋的基于烈度的易损性矩阵。
2.2 土木结构房屋易损性曲线本文首先以孙柏涛等(2014)统计给出的III区土木结构易损性矩阵为例,计算结构超越概率易损性曲线。图 3为分别以散点图和直方图来直观地表达III区土木结构房屋在不同烈度作用下的破坏比结果。
通过基于烈度的土木结构房屋易损性矩阵,从破坏状态DSi的破坏概率累积计算出超越每个极限破坏状态LSi的累计概率,得到相应土木结构房屋的超越概率矩阵,详见表2。
通过最大似然估计法,结合表 1,利用MATLAB软件即可求得土木结构房屋超越概率,计算得到其对数正态分布的易损性函数双参数θ和β,如表3所示。
表2 III区土木结构房屋超越概率矩阵(%)
Tab.2 Exceedance probability matrix of civil structure buildings in III zone(%)图3 III区土木结构房屋震害矩阵散点图(a)及直方图(b)
Fig.3 Scatter diagram(a)and histogram(b)of damage probability matrix of civil structure buildings in III zone表3 III区土木结构房屋不同极限状态下超越概率易损性曲线θ和β
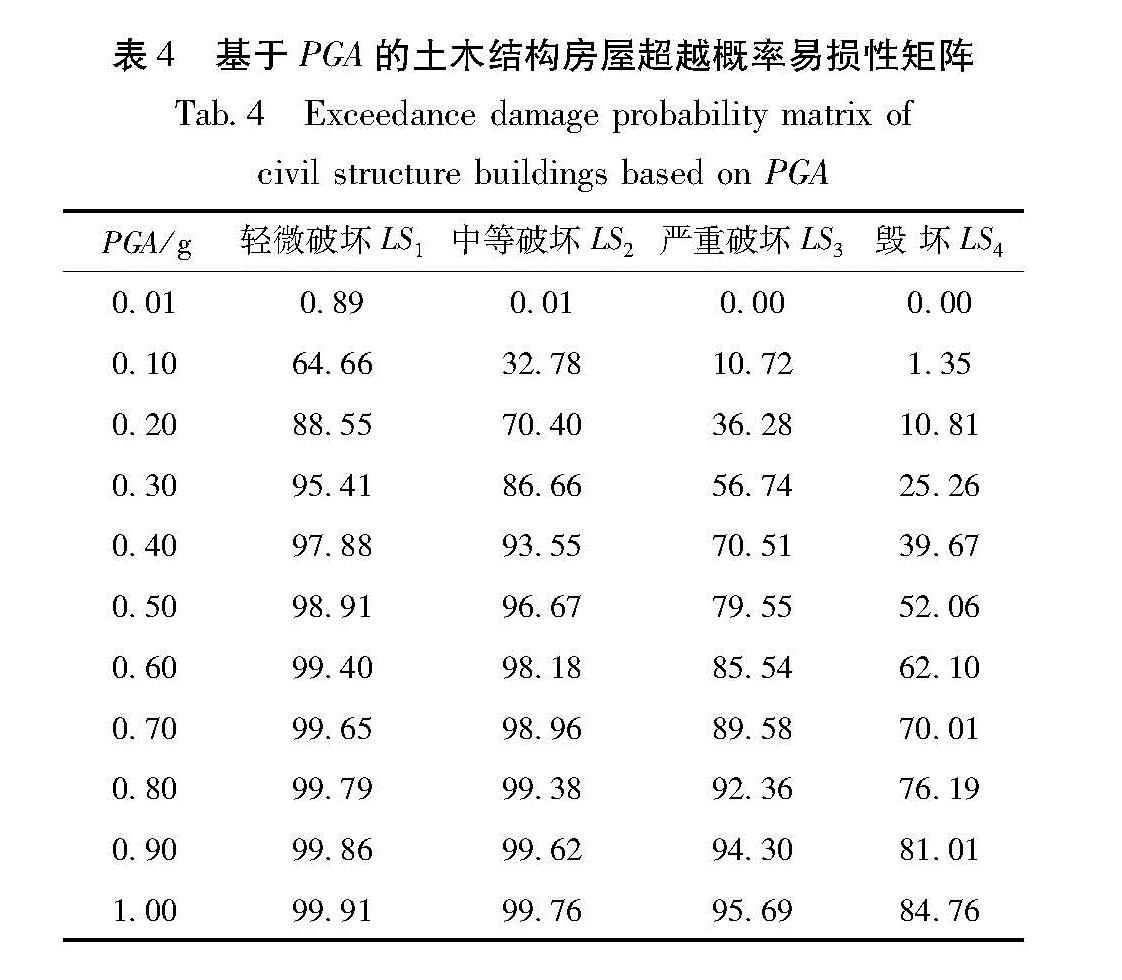
Tab.3 Medianand θ and standard deviation β of the exceedance probability of the civil structure buildings in different limit states in III zone采用易损性曲线双参数θ和β即可绘制出III区基于地震动参数PGA土木结构房屋的超越概率易损性曲线,如图4所示。超越概率的离散点是通过实际震害资料调查计算得到的,与最大似然估计法拟合的易损性超越概率校核曲线一致,可以得到理论分析的最大似然估计曲线是合理的、准确的。由此通过拟合的易损性曲线可以得到不同PGA(单位:g,1 g=9.8 m/s2)对应的不同破坏状态的超越概率(表4)。
表4 基于PGA的土木结构房屋超越概率易损性矩阵
Tab.4 Exceedance damage probability matrix of civil structure buildings based on PGA为了得到处于不同破坏状态的概率,用PDSk表示在DSk状态下的概率; PLSs表示极限破坏状态的概率。结构不同破坏状态下的损害概率,通过以下公式求得:
PDS0(xi)=1-PLS1(xi)(7)
PDSk(xi)=PLSk(xi)-PLSk+1(xi)=
Φ((ln((xi)/(θLSk)))/(βLSk))-Φ((ln((xi)/(θLSk+1)))/(βLSk+1))(8)
式中:k=1,2,3。
PDS4(xi)=PLS4(xi)(9)
根据土木结构易损性超越概率曲线结果,结合表4,通过式(7)~(9)可以得到不同破坏状态下的易损性矩阵,如表 5所示。
通过式(7)~(9)绘制基于PGA土木结构房屋的易损性曲线,如图5所示,可直观看到不同破坏状态的损害概率随PGA增大的变化趋势,得到给定PGA下结构超越不同破坏状态的概率。
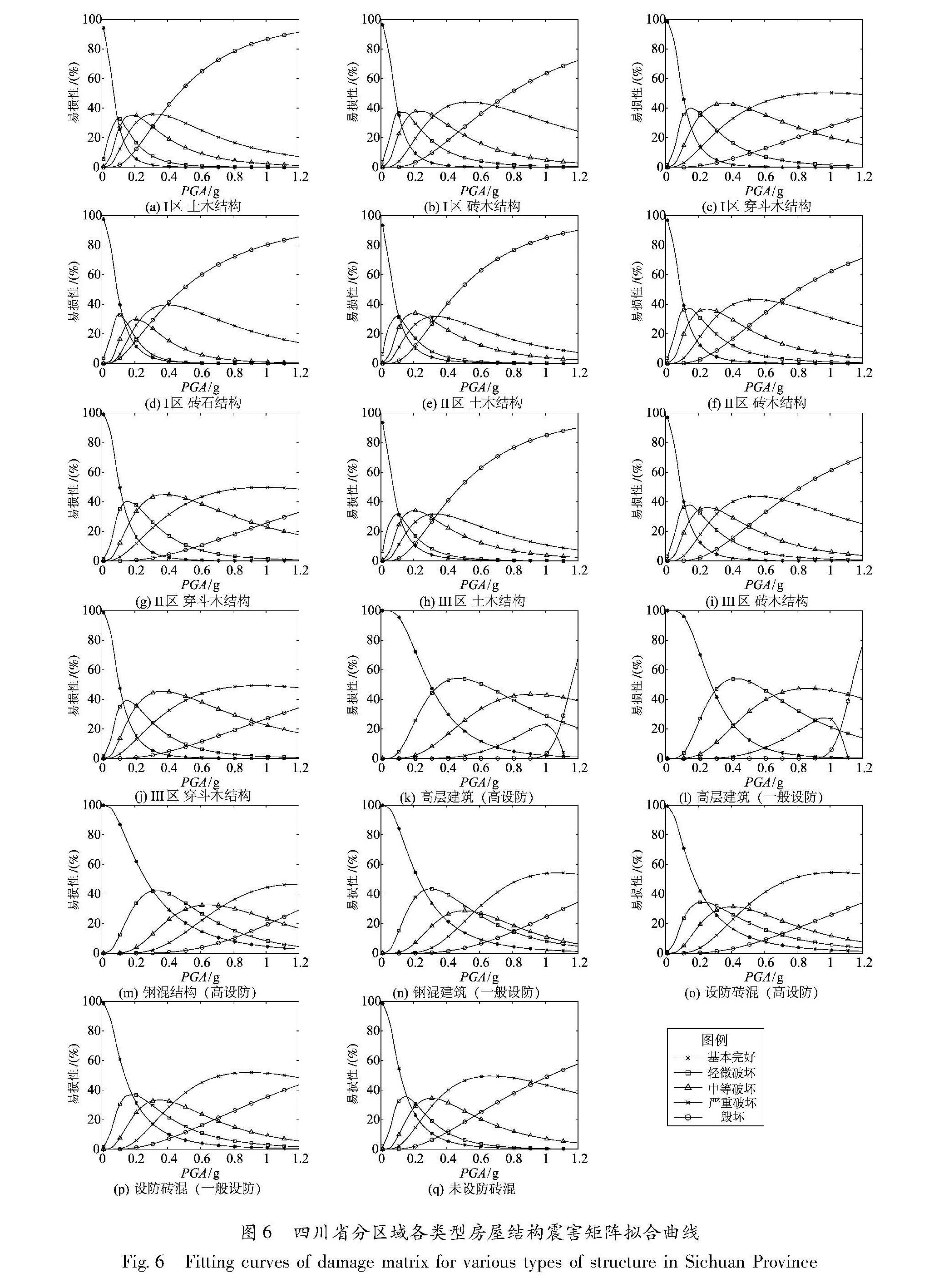
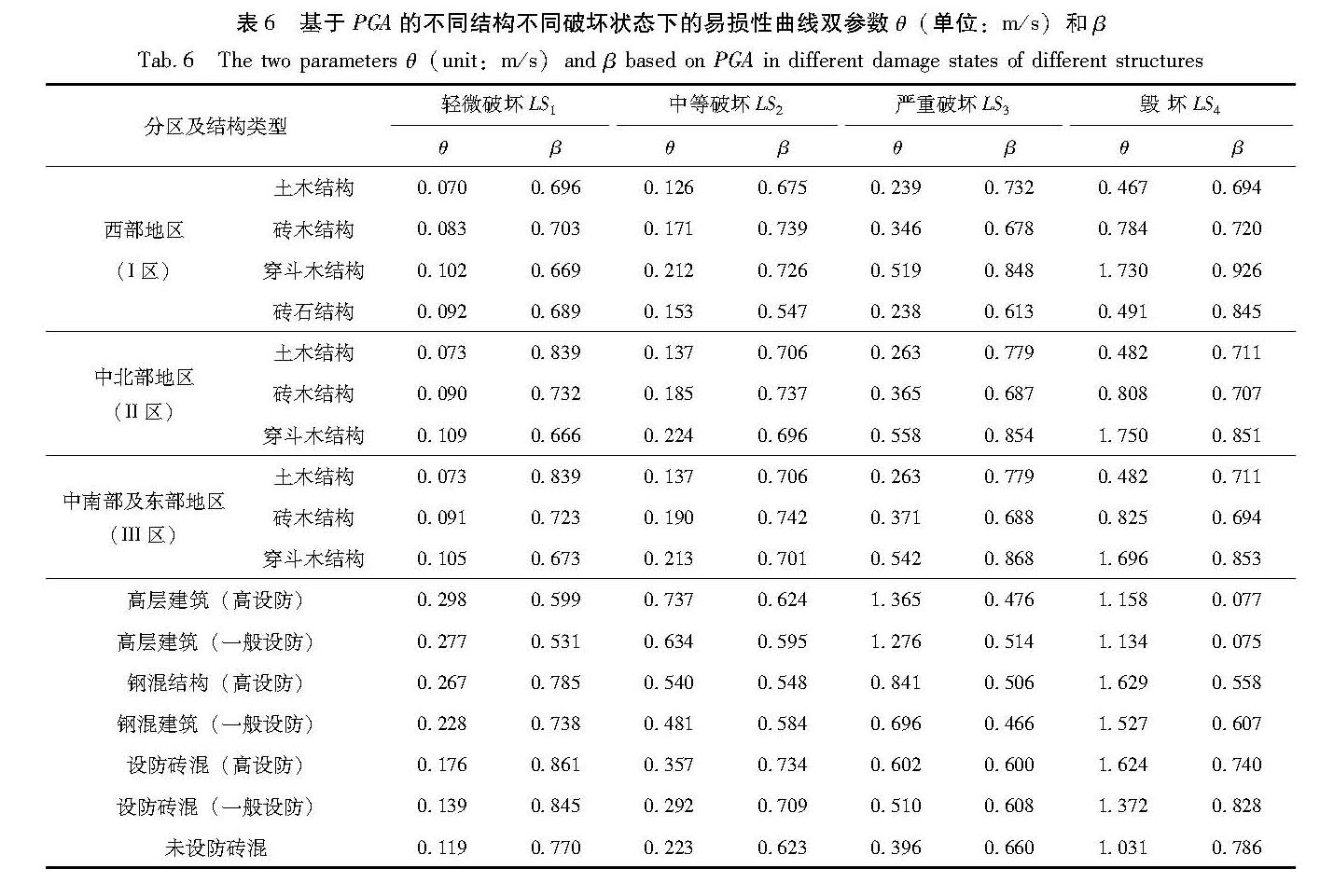
2.3 多种房屋建筑的易损性曲线与III区土木结构房屋易损性曲线计算一致,通过最大似然估计方法,利用烈度与PGA之间的对应关系,本文将提供不同结构处于不同破坏状态下的易损性函数的双参数θ和β,并绘制出其易损性曲线,如表 6所示。基于易损性曲线双参数绘制四川省3个分区不同类型结构的易损性曲线,如图 6所示。
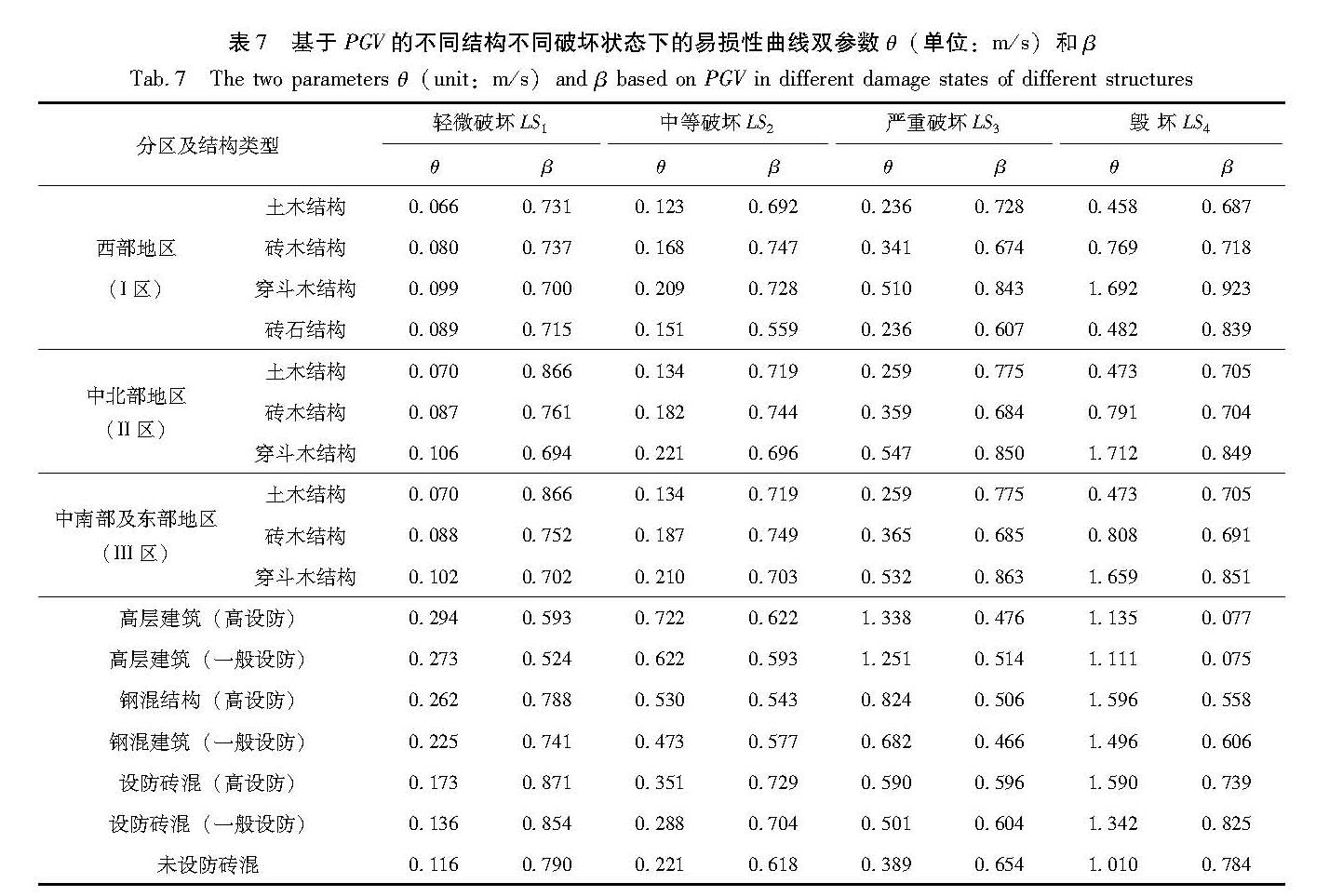
按照烈度与PGV之间的对应关系,同样可以给出了基于PGV的不同结构房屋在不同破坏状态下的θ和β,如表7所示。
3 结论与讨论
本文提出一种房屋震害矩阵双参数曲线化方法,该方法基于烈度与地震动参数之间的对应关系,采用最大似然估计方法,将既有房屋易损性矩阵或实际震害统计的破坏比结果转化为双参数易损性曲线。具体认识如下:
(1)该方法弥补了基于烈度易损性曲线的不足,特别是针对难以进行模拟分析的结构类型,如土木结构、砖石结构等简易房屋,提供了更为简便的途径来得到相应的易损性曲线。
(2)以四川省房屋震害矩阵为例,基于中国地震烈度表中烈度与地震动参数的关系,给出了各类房屋结构的地震易损性曲线特征参数,分析结果可为四川省基于地震动参数的房屋建筑震害评估提供基础数据。需要注意的是,在实际工程应用中,针对不同的区域特征,应合理选择烈度-地震动参数(PGA,PGV)的关系模型。
图6 四川省分区域各类型房屋结构震害矩阵拟合曲线
Fig.6 Fitting curves of damage matrix for various types of structure in Sichuan Province表6 基于PGA的不同结构不同破坏状态下的易损性曲线双参数θ(单位:m/s)和β
Tab.6 The two parameters θ(unit:m/s)and β based on PGA in different damage states of different structures表7 基于PGV的不同结构不同破坏状态下的易损性曲线双参数θ(单位:m/s)和β
Tab.7 The two parameters θ(unit:m/s)and β based on PGV in different damage states of different structures(3)本文提出的易损性矩阵曲线化方法具有较高的可靠性和适用性,在进一步研究工作中可应用该方法对已有的易损性矩阵或曲线进行校验和完善,以便更好地服务于地震灾害快速评估、风险评价和保险估算等。
考虑到目前直接获取的强震记录均为未修正的结果,烈度与地震动参数对应关系还需要进一步完善,本文通过基于房屋震害矩阵曲线化方法得到的易损性曲线与真实情况相比存在一定误差。随着烈度与地震动参数对应关系的完善,本文方法可得到更加广泛的应用。
- 陈力波,郑凯锋,庄卫林,等.2012.汶川地震桥梁易损性分析[J].西南交通大学学报,47(4):558-566.
- 韩淼,刘健兵,高孟潭.2009.地震设防水准对典型框架土建成本的影响[J].震灾防御技术,4(2):209-214.
- 胡少卿,孙柏涛,王东明,等.2007.经验震害矩阵的完善方法研究[J].地震工程与工程振动,27(6):46-50.
- 胡聿贤,张敏政.1984.缺乏强震观测资料地区地震动参数的估算方法[J].地震工程与工程振动,4(1):3-13.
- 胡聿贤.2006.地震工程学[M].北京:地震出版社.
- 李静,陈健云,温瑞智.2012.框架结构群体震害易损性快速评估研究[J].振动与冲击,31(7):99-103.
- 林庆利,林均岐,刘金龙.2017.汶川地震公路桥梁易损性研究[J].振动与冲击,36(4):110-118.
- 刘如山,胡少卿,邬玉斌,等.2009.基于地震动参数的结构易损性表达方法研究[J].地震工程与工程振动,29(6):102-107.
- 马玉宏,赵桂峰,陈小飞,等.2015.村镇建筑基于性态抗震设防的地震保险费率厘定[J].地震研究,38(3):461-466.
- 明小娜,周洋,钟玉盛,等.2017.2017年云南鲁甸MS4.9地震房屋震害特征与烈度评定[J].地震研究,40(2):295-302.
- 孙柏涛,陈洪富,闫培雷,等.2014.南北地震带房屋建筑抗震能力分区特征研究——以四川省为例[J].土木工程学报,(增刊1):6-10.
- 田启文,廖振鹏,孙平善.1986.根据烈度资料估算我国地震动参数衰减规律[J].地震工程与工程振动,6(1):21-36.
- 温增平,徐超,陆鸣,等.2009.汶川地震重灾区典型钢筋混凝土框架结构震害现象[J].北京工业大学学报,35(6):753-760.
- 吴子燕,贾兆平,刘骁骁.2014.基于桥梁经验数据的理论易损性曲线校准[J].应用数学和力学,35(7):723-736.
- Aldemir A,Erberik M A,Demirel O,et al.2013.Seismic Performance Assessment of Unreinforced Masonry Buildings with a Hybrid Modeling Approach[J].Earthquake Spectra,29(1):33-57.
- Baker J W.2013.Efficient Analytical Fragility Function Fitting Using Dynamic Structural Analysis[J].Earthquake Spectra,31(1):579-599.
- Colombi M,Borzi B,Crowley H,et al.2008.Deriving vulnerability curves using Italian earthquake damage data[J].Bulletin of Earthquake Engineering,6(3):485-504.
- Lagomarsino S,Cattari S.2014.Fragility Functions of Masonry Buildings[M]// SYNER-G:Typology Definition and Fragility Functions for Physical Elements at Seismic Risk.Berlin:Springer Netherlands:111-156.
- Shinozuka M,Banerjee S,Kim S.2007.Fragility Considerations in Highway Bridge Design[R].Buflalo:Mutidiscip linary Center for Earthquake Engineering Reasearch.
- Shinozuka M,Feng M Q,Lee J,et al.2000.Statistical Analysis of Fragility Curves[J].Journal of Engineering Mechanics,126(12):1224-1231.
- Singhal A,Kiremidjian A.1998.Bayesian updating of fragilities with application to RC frames,124(8):922-929.
- Yamazaki F,Motomura H,Hamada T.2000.Damage assessment of expressway networks in Japan based on seismic monitoring[C].Auck land,New Zealand:12th World Conference on Earthquake Engineering.
- GB/T 17742—2008,中国地震烈度表[S].
- GB/T 24335—2009,建(构)筑物地震破坏等级划分[S].