基金项目:国家重点研发计划政府间科技创新合作重点专项——中国大陆中强地震前后地震活动性演化研究(2016YFE0109300),自然基金国际和地区合作基金——呼图壁储气库地震活动性特征及其机理研究(41561164018),自然基金——新型主动气枪震源激发信息的提取与分析(41790462)及国家自然科学基金(41474051)——呼图壁储气田充放气引起地下应力变化的地震学观测联合资助.
(Key laboratory of Seismic Observation and Geophysical Imaging,Institute of Geophysics,China Earthquake Administration,Beijing 100081,China)
active seismic source; airgun seismic source; untuned large-volume airgun; deconvolution
备注
基金项目:国家重点研发计划政府间科技创新合作重点专项——中国大陆中强地震前后地震活动性演化研究(2016YFE0109300),自然基金国际和地区合作基金——呼图壁储气库地震活动性特征及其机理研究(41561164018),自然基金——新型主动气枪震源激发信息的提取与分析(41790462)及国家自然科学基金(41474051)——呼图壁储气田充放气引起地下应力变化的地震学观测联合资助.
利用云南宾川主动源资料,对比分析了阻尼系数法、水准法、最小二乘法、时间域迭代法以及维纳法去除气枪信号震源响应的效果。结果 表明:①在参数选择正确时,以上方法得到的波形差异不大。其中阻尼系数法、水准法参数选取难度最大,最小二乘法虽然能够自动找到最优解,但步长设置过小时,计算效率低,步长设置过大时,易出现假极值点。时间域迭代法及维纳法的参数对结果的影响相对较小。②对于高信噪比叠加信号,时间域迭代法得到的信号信噪比最高,计算时间对比其他方法增加不大,是一种较好的反褶积方法。对于单枪低信噪比信号,当只需要到时信息时,可使用时间域迭代法,但需波形信息时,从波形的可信度及计算效率上考虑,维纳法是更加折中的方法。
Using airgun data from Binchuan in Yunnan Province,we compare the calculation effects of damping factor method,water level method,least squares method,time domain iteration method and Wiener method on the removal of the time function. The results show that:① The waveforms obtained by the above methods have little difference when the parameters are correctly selected. The damping coefficient method and water leveling method are the most difficult to choose. The least squares deconvolution can automatically find the optimal solution,but the calculation efficiency is too low if the step size is set too small,and false extreme points are likely occurred when the step size is set too large. The parameters of the time domain iteration and Wiener method have relatively little influence on the results.② For high signal-to-noise ratio(SNR)stacked signals,the SNR obtained by the time domain iterative deconvolution method is the highest,and the computation time is within the accepted range,so it is a good deconvolution method. For single-gun low SNR signals,the time domain iterative method can be chosen when we just need to pick the arrival time. But when waveform information is needed,the Wiener method is more effective in terms of the reliability of the waveform and the calculation efficiency.
引言
分析地震波是了解地球内部结构、组成、状态和演化的有效手段(陈颙,朱日祥,2005)。利用人工震源对区域地下结构进行探测是研究地球内部结构及介质特性的一种新型手段。20世纪60年代,气枪震源开始应用于海洋勘探,至今已取得巨大成就。近年来,中国地震局将海上气枪主动源引入陆地,建立了包括宾川在内的多个试验场,开展了大量实验工作,获得了丰富的数据。研究发现,大容量气枪震源与其他勘探手段相比有着激发性能高、可重复性好、绿色环保、安全性高的优点,应用前景广阔(陈颙等,2007; 林建民等,2008; 王伟涛等,2017)。
台站间的格林函数直接携带台站区域的地下结构信息(许立生,陈运泰,1996)。为得到格林函数,需要用反褶积计算去除观测信号中震源的影响。气枪激发时气泡子波的混叠效应使得气枪的观测信号相比天然地震信号更为复杂,反褶积后可得到更为清晰的震相(Wang et al,2018; Yang et al,2018),故在处理气枪信号资料时,反褶积运算十分必要。许多更深入的研究建立在反褶积计算的结果之上,但是实际观测信号中存在背景噪声及仪器噪声,这些噪声对计算结果的稳定性与真实性有极大的影响。为解决此问题,很多反褶积数学方法被提出(Bell,Sejnowski,1995; Helmberger,Wiggins,1971; Sheehan et al,1995),虽然这些方法的数学模型是确定的,并在一定程度上能消除噪声的影响,但是模型的参数需要根据数据质量半经验进行选取,这些参数将直接影响反褶积效果(Lines,Treitel,1984),并且每种方法的处理效率及适用的信号也不同。因此,为不同质量的气枪信号选取较为合适的反褶积方法及参数十分重要。为对比不同方法的运算效果及处理效率,本文将频率域内的阻尼系数法、水准因子法、最小二乘法、时间域迭代法及维纳法应用于云南宾川气枪主动源资料对比不同方法的计算效果。
1 反褶积方法原理
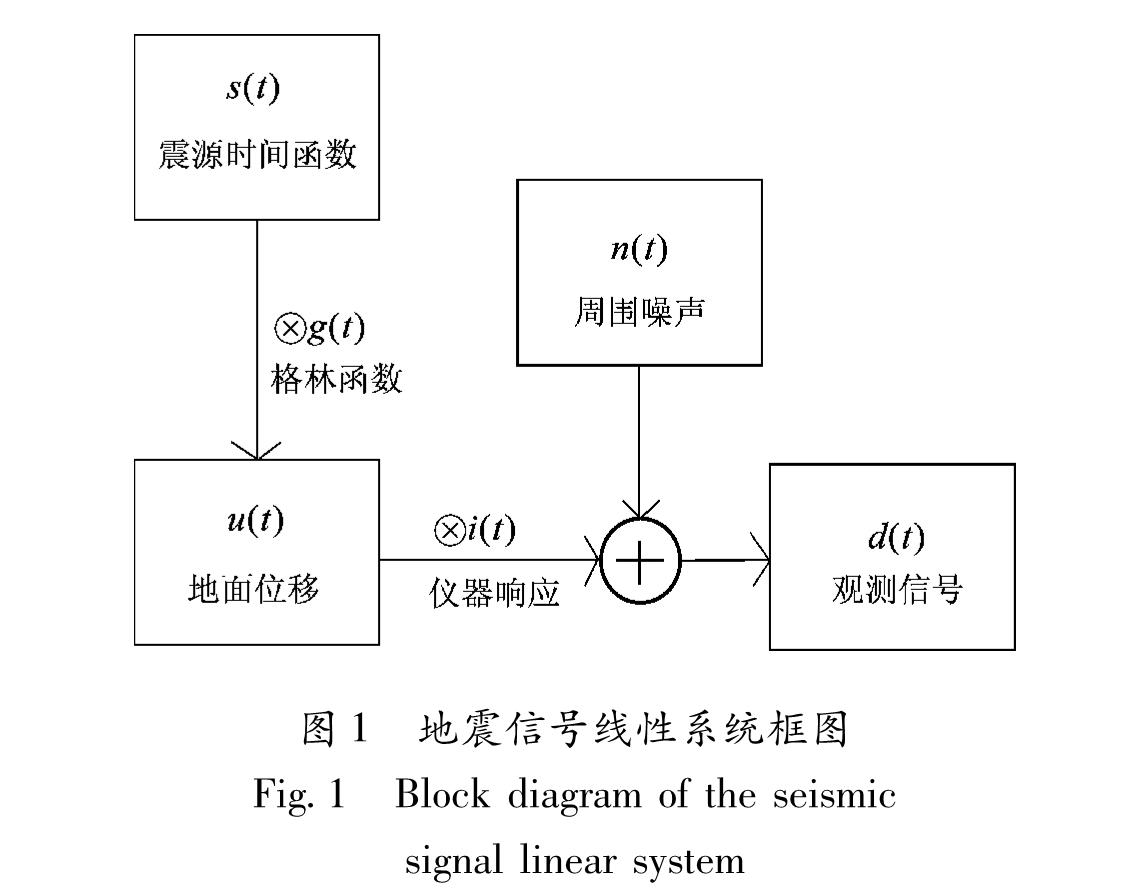
地震波的观测信号d(t)可表示为:
d(t)=s(t)g(t)i(t)+n(t)(1)
式中:是卷积符号; s(t)为震源时间函数; g(t)为格林函数; i(t)为台站仪器内部对信号的脉冲响应; n(t)为观测信号的周围噪声。
图1为式(1)所表达的线性系统,该系统由2个褶积模块和1个叠加模块组成。系统输入震源时间函数s(t),输出观测信号d(t)。
在实际的数据处理中忽略周围噪声影响,并去除仪器响应,可得:
u(t)=s(t)g(t)(2)
求解格林函数转化为s(t)的反褶积,在气枪信号处理过程中,s(t)可由震中距较小的参考台接收到的信号近似代替。
一般来说,2个信号在时间域中的褶积等于这2个信号在频率域中的乘积:
u(ω)=s(ω)g(ω)(3)
g(ω)=(u(ω))/(s(ω))(4)
故频率域的反褶积可直接转化为除法,但地震波信号通常具有高频截止性,而噪声信号通常又是高频的,在两者相除时震源时间函数中的高频噪声会被放大,造成解的不稳定性(Gurrola et al,1995)。为改善解的这一问题,一些反褶积算法被提出。
1.1 阻尼系数法阻尼系数法假设噪声全部为具有零均值的高斯随机噪声。调整后的反褶积表达式为:
g(ω)=(u(ω)s*(ω))/(s(ω)s*(ω)+δ)(5)
式中:*代表复共轭; δ为阻尼系数。
数学上,阻尼系数的加入相当于在分母中加入一个不为零的常数,减小了分母接近零时的影响,提高解的稳定性。物理上,阻尼系数在分母项的能量谱密度中加入了白噪声(图2a),大幅度提高了低频部分信号功率,故而减小了高频噪声对计算结果的影响。阻尼系数的引入本质上相当于加入了一个低通滤波器。当阻尼系数等于零时,式(5)退化为直接求频率域反褶积公式(4)。阻尼系数的大小通常根据信号的噪声水平及功率谱密度峰值半经验的选取,当阻尼系数的值选择过小时,稳定效果不明显; 数值过大时,分母将趋于常数,所以参数的选择十分重要。
1.2 水准法水准法阻尼系数法非常相近,基本假设也相同,将式(5)改进为:
g(ω)=(u(ω)s*(ω))/(max{s(ω)s*(ω),max[s(ω)s*(ω)]c})(6)
式中:c为水准比例因子。
阻尼系数法将分母能量谱密度中每一个频率的振幅都加了一个常数,而水准法是选定一个阈值,这个阈值由水准比例因子c乘以能量谱密度的峰值所确定,当分母的能量谱密度的振幅超过水准阈值时保持不变,低于阈值时提升到水准阈值(Menke,1984)(图2b)。水准法也相当于对分母的能量密度谱做了一个低通滤波,通过向低于水准阈值的部分加入白噪声而提升了分母能量谱密度的带宽。水准比例因子的大小同样需要半经验的选取,当水准比例因子过大时分母将趋于常数。
1.3 最小二乘法最小二乘法由Bostock(1998)提出,原理与阻尼系数法相同,只是阻尼系数δ无需自行选择。使交叉验证函数(GCV)值最小的δ值即为最佳的阻尼系数。GCV函数定义如下:
GCV(δ)=(∑Mm=1∑Nn=1[um(ωn)-sm(ωn)g(ωn)]2)/([MN-∑Nn=1Χ(ωn)]2)(7)
Χ(ω)=(∑Mm=1sm(ω)sm*(ω))/([∑Mm=1sm(ω)sm*(ω)+δ]2)(8)
式中:N为在对原信号进行傅里叶变换时的频率采样点的个数; ωn为对应的频率; M为地震信号的个数。
式(7)分子为预测信号与实际观测信号的残差平方和(RSS)用来评估预测值与实际值的吻合程度。分母中的M,N用来衡量模型的自由度,X用来衡量阻尼因子δ的引入对原始模型的改变。
GCV是一种从回归分析中引入的正则化方法。选定初始δ和迭代步长后,反复迭代求得GVC函数,并找出使GCV函数最小的δ值,即最佳的δ值。最后将最佳的δ值带回式(5)求得最终反褶积结果。
初始假设同样是认为数据中的噪声为白噪声,但对噪声的能量及振幅的分布没有特别的假设(Bostock,1998)。
1.4 时间域迭代法时间域迭代法依赖互相关函数,并通过迭代构造格林函数(Kiknchi,Kanamori,1982)。具体方法步骤为:
①通过互相关扫描式(9),求得u(t)与s(t)互相关函数(rsu)平方最大时所对应的时间延迟t1:
rsu(t')=∫∞∫0s(t)u(t+t')dt(9)
[rsu(t1)]2=maximum(10)
②通过式(11)和(12)求得幅值m1,预测信号可表示为式(13):
rs(t')=∫∞∫0s(t)s(t+t')dt(11)
m1=rsu(t1)/rw(0)(12)
u1pre=s(t)m1δ(t-t1)(13)
③用原始信号u(t)减去预测信号u1pre(t)得到新的观测信号u1(t),迭代步骤①,②,直至原始信号与预测信号的残差平方和不再大于某个阈值。
原始信号和格林函数可以分别表示为:
u(t)=∑Ni=1uipre(t)=s(t)∑Ni=1m1δ(t-t1)(14)
g(t)=∑Ni=1m1δ(t-t1)(15)
最后利用带通滤波去除高频噪声的影响。
1.5 时间域维纳法在时间域内可以将观测信号看成格林函数与震源时间函数的褶积,将格林函数视为滤波器的脉冲响应,将震源时间函数和观测信号分别看做滤波器的输入和输出。但事实上无法得到这样的滤波器,只能得到它的近似估计:
u~(t)=s(t)g(t)(16)
假设s(t)的激励下滤波器的实际输出u~(t), 与期望输出u(t) 尽可能相似,取误差平方和最小,即:
Q=∑[u~(t)-u(t)]2(17)
对式(17)求极小,可得如下矩阵方程:
[a0 a1 a2 … an
a1 a0 a1 … an-1
an an-1 an-2 … a0][g0
g1
gn]=[c0
c1
cn](18)
式中:gτ为待定格林函数的时间序列; aτ为震源时间函数的自相关; cτ为震源时间函数与观测信号的互相关。对该方程求解即得到格林函数(吴庆举等,2003)。
2 处理流程
2.1 数据选择云南宾川地震信号发射实验台位于红河断裂与程海断裂之间,坐落于大银甸水库,由4支容量为2 000 in3的气枪组成,每次激发相当于ML0.7地震。气枪放置深度为10 m,自2012年9月建成后,每周激发20次,2014年9月后每周激发60次(陈佳等,2017)。接收系统仪器由Reftek 130数据采集器和频带范围为2 s~100 Hz的短周期Guralp CMG-40T 地震计组成。本文选用2014年震中距为17 km的53258台(图3a)的资料。此台从未发生过替换,数据连续率为91%,工作稳定(张云鹏等,2017)。参考台的选用频带范围为2 s~100 Hz,距信号发射台40 m的CKT1台。因先叠加后反褶积的处理流程的结果在信噪比、计算效率等方面优于先反褶积后叠加(翟秋实等,2016),故在反褶积前使用RMS线性叠加方法(蒋生淼等,2017)共叠加1 092条Z分量数据,以提高信噪比(图3b,c)。
2.2 数据处理流程为提高信号信噪比,在对观测数据做反褶积前后,需要进行滤波及信号叠加,操作流程如下:
①去均值,去线性趋势。
②带通滤波:气枪源的优势频带为3~7 Hz(杨微等,2013),在进行反褶积前进行2~8 Hz的带通滤波。
③信号叠加:对于气枪源,RMS筛选叠加能有效提高噪声地震记录和小地震信号事件(蒋生淼等,2017)。使用RMS线性叠加方法对53258台的信号进行叠加,提高信噪比。
④使用不同方法进行反褶积。
⑤带通滤波:因为反褶积稳定性较差,在反褶积之后还需要进行带通滤波,本次带通滤波频带设置为2.5~5 Hz。
3 计算结果
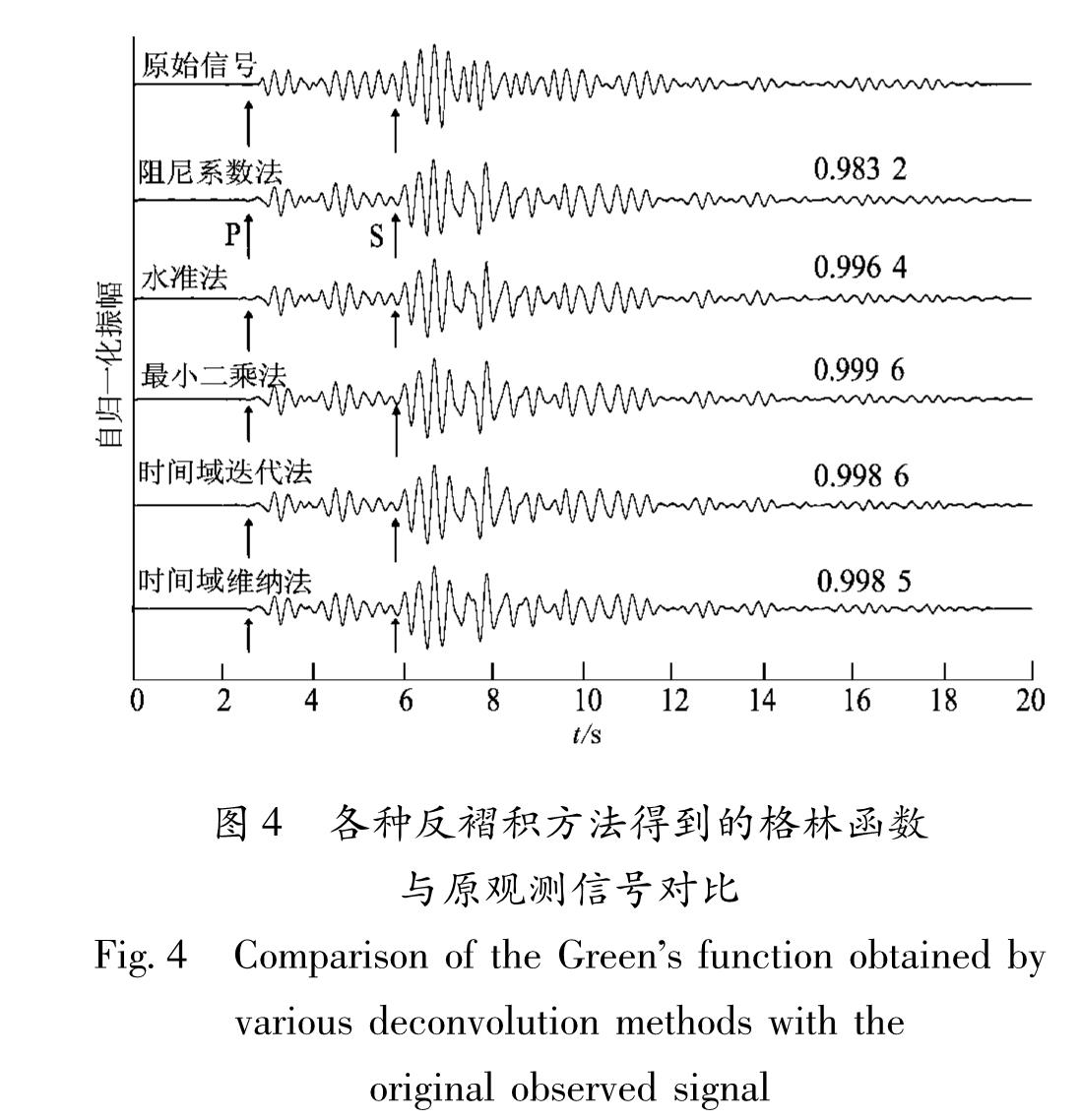
经过不断调整参数,最终得到5种反褶积方法最佳的格林函数,如图4所示。使用阻尼系数法时选取阻尼系数为1010; 使用水准法时选取水准比例因子为10-4; 用最小二乘法时,使交叉对比函数最小对应的阻尼系数值为1.78×1010; 使用时间域迭代法时,设定迭代次数为2 000次或数据残差小于0.005时终止迭代。
为了验证所得格林函数的稳定性,计算了格林函数与参考信号褶积所得的信号和原观测信号的互相关系数,对应于图4右侧数字。从图中可以发现,当观测信号信噪比较高且反褶积的参数设置正确时,每种方法计算得到的相关系数都在0.9以上,其中最小二乘法求得的互相关系数最高。同时所有方法都能使S震相变得更加清晰,减小了原始信号受到气枪激发时气泡子波混叠的影响。为进一步对比各种方法的区别,研究了各种方法参数的影响、计算效率及信噪比。
4 讨论
4.1 参数影响由图4可知,在叠加信号信噪比较高且参数选取正确时,各反褶积方法的计算结果十分相近。鉴于参数的选择难度以及当参数选取不正确时对反褶积结果的影响不同,故对参数的影响做进一步讨论。
(1)阻尼系数法:阻尼系数在震源子波的能量谱密度中加入白噪声,降低解的不稳定性。从图5可以看出,随着阻尼系数的变大,震源时间函数功率谱密度的峰值会被迅速提高,造成格林函数振幅被迅速缩小。
图5 阻尼系数分别取1010(a)、1013(b)、1014(c)时所对应的格林函数
Fig.5 The corresponding Green's function is obtained when the damping coefficients are taken as 1010(a), 1013(b)and 1014(c)respectively(2)水准法:在频率域反褶积时,水准比例因子的选取是一个难点,该因子越大反褶积结果越稳定,但失真度也越大。因此需要根据数据质量多次尝试选择水准比例因子(翟秋实等,2016)。水准法不改变震源时间函数的能量谱密度峰值,不会出现格林函数振幅严重衰减的情况,如图6所示。从图5,6可见,阻尼系数法参数的变化对计算结果的影响显著,而水准法得到的结果更加稳定。
(3)最小二乘法:该方法是一种通过试解自动寻找最佳阻尼系数的方法。实际应用中发现,阻尼系数的量级一般在1010左右,试解运算时,步长设置过大易出现错误的极点,步长过小计算量大、效率低,但阻尼因子系数的取值更加精准。
图6 水准比例因子分别取10-6(a)、10-4(b)、10-1(c)时所对应的格林函数
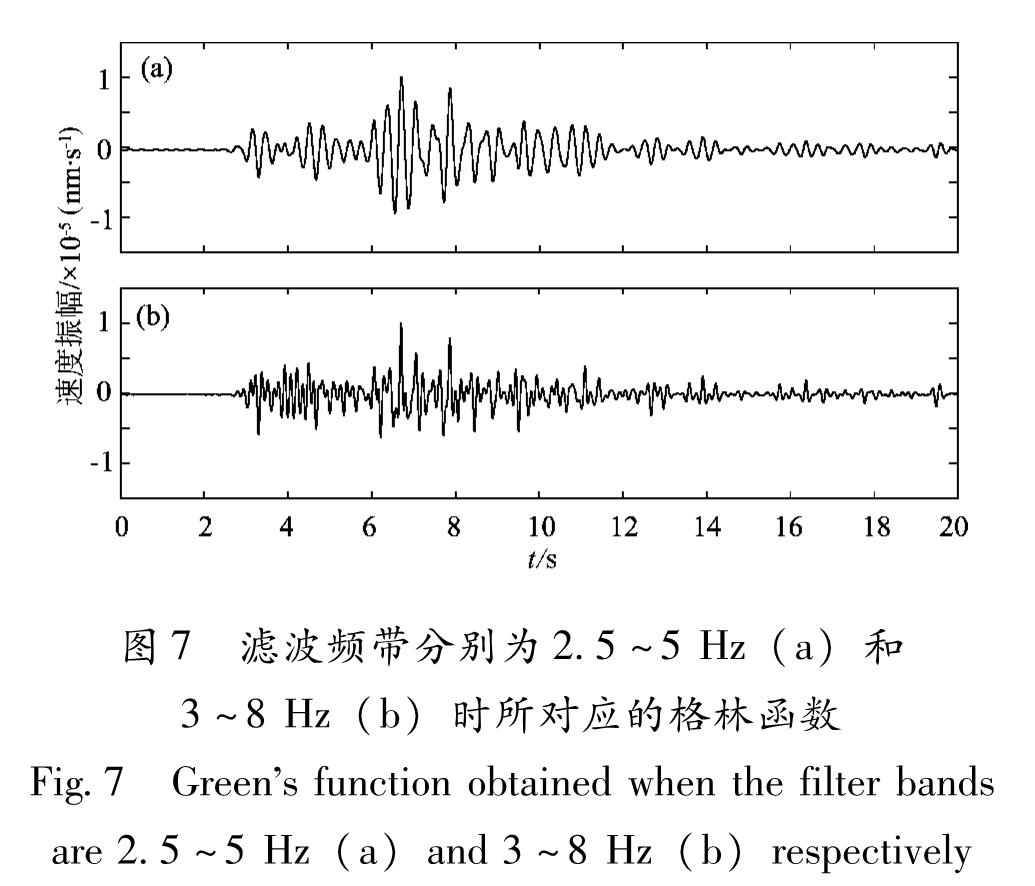
Fig.6 The corresponding Green's function is obtained when the water level scale factor is 10-6(a), 10-4(b)and 10-1(c)respectively(4)时间域迭代法:由于时间域迭代反褶积此方法是将格林函数近似的看作由一些平移缩放的δ函数组成,势必会引入其他频带的噪声,故反褶积后的带通滤波频带的选择十分重要。频带选择不当将出现波形信号变形。从图7中可以看出当滤波频带选为3~8 Hz时,出现大量高频噪声。但对于气枪源优势频带较窄,其处理效果较好。
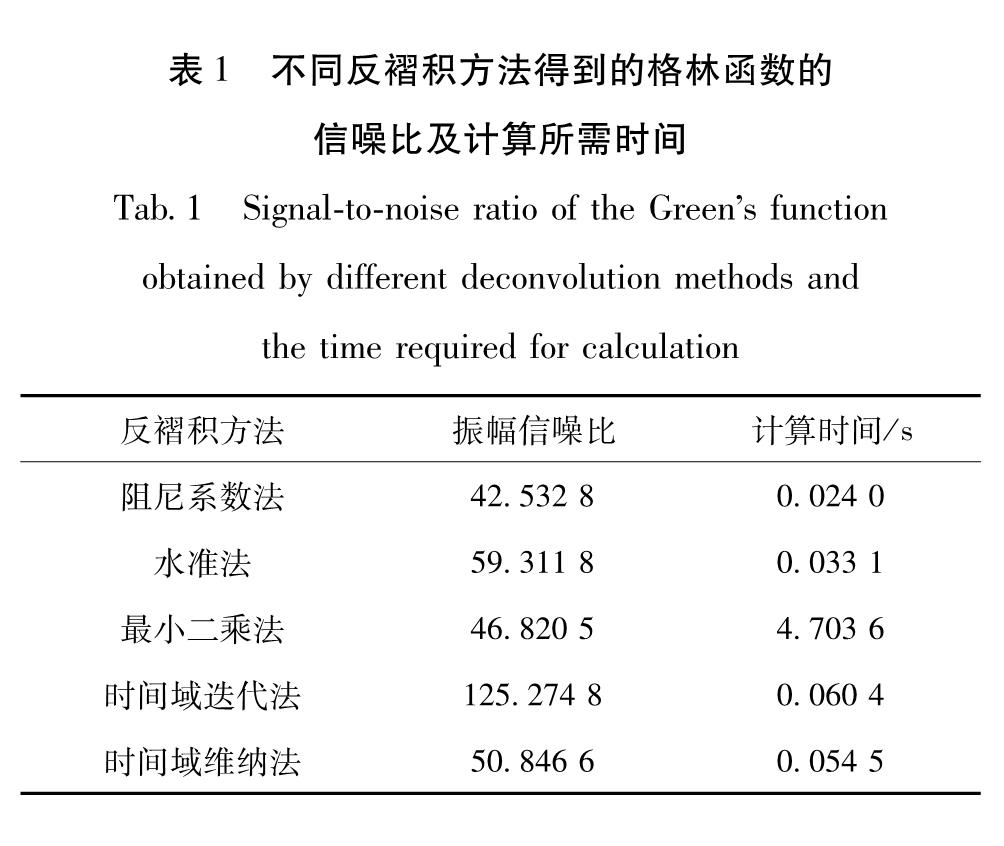
(5)时间域维纳法:该方法与最小二乘法原理相近,都是以最小均方误差作为输出准则,但最小二乘法是在频率域内求解,而维纳法是在时间域求解。在求解矩阵方程时由于构造的托普利斯矩阵为病态矩阵,解是不稳定的,需要加入白噪声,本文研究预白百分比为0.01%。加入白噪声后矩阵的条件数由108降到105。4.2 信噪比及计算效率信噪比是衡量信号质量的重要标准,本文对比了不同反褶积方法得到的格林函数的振幅信噪比,并计算了反褶积计算所需的时间以衡量各方法的计算效率,如表1所示。其中选取P波到时前2 s为背景噪声时窗,P波到时后7 s为信号时窗。
表1 不同反褶积方法得到的格林函数的信噪比及计算所需时间
Tab.1 Signal-to-noise ratio of the Green's function obtained by different deconvolution methods and the time required for calculation从表1中可以发现,时间域反褶积得到的信号信噪比最高,这是因为时间域反褶积通过互相关扫描拾取振幅最大的位置近似为狄拉克函数,能够有效压制小振幅的背景噪声,将低于阈值的信号直接置0。从计算效率上讲,虽然最小二乘法及时间域迭代法都需要进行迭代,但时间域迭代法的计算时间远远小于最小二乘法。
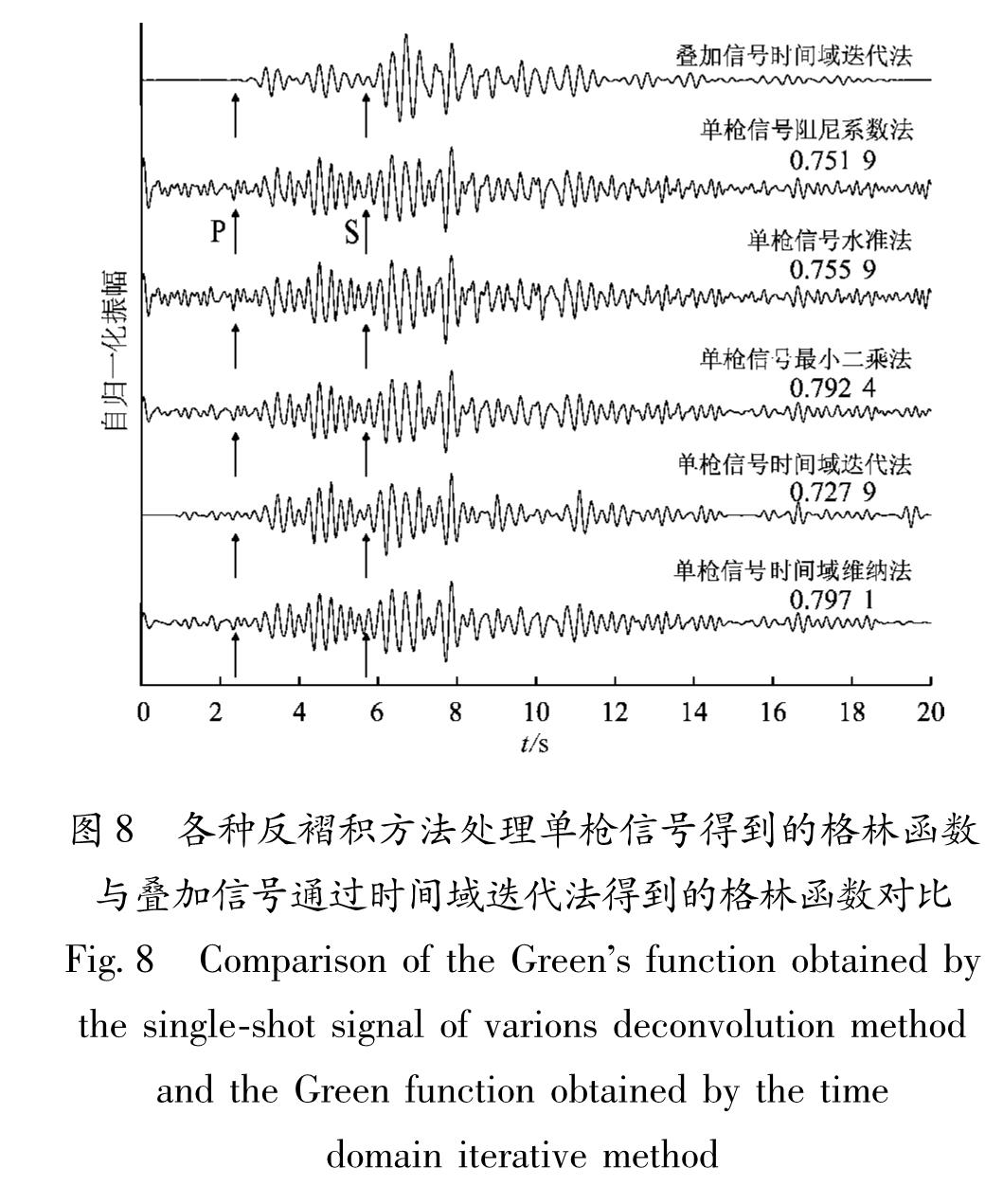
4.3 低信噪比信号运算上述方法均使用在经过叠加的高信噪比信号上,而低信噪比信号的运算效果也是衡量反褶积算法稳定性的标准。本文使用不同反褶积方法对具有较低信噪比的单次激发信号的计算效果进行比较。选择2014年1月2日17时整激发的气枪信号,处理结果如图8所示。从图中可以看出,相对于频率域,时间域的反褶积方法得到的格林函数有着更好的信噪比,能够更好地识别P波、S波到时。且时间域迭代法比维纳法信噪比更高,但各个方法得到的单次激发格林函数相比叠加信号的格林函数波形都有所变形。为量化各个方法得到波形的变形情况,图8右侧数字表示单枪信号格林
图8 各种反褶积方法处理单枪信号得到的格林函数与叠加信号通过时间域迭代法得到的格林函数对比
Fig.8 Comparison of the Green's function obtained by the single-shot signal of varions deconvolution method and the Green function obtained by the time domain iterative method函数与叠加信号格林函数的相关系数,最小二乘法和时间域维纳法得到的格林函数波形变形较小,时间域迭代法得到的格林函数虽然信噪比较高,但波形变形最严重。
5 结论
本文利用云南宾川主动源资料,对比分析了阻尼系数法、水准法、最小二乘法、时间域迭代法以及维纳法去除气枪信号震源响应的效果,得到如下结论:(1)阻尼系数法和水准法需要通过试错法找出最优解,参数选取难度最大; 最小二乘法能够自动化找到最优解,但迭代步长设置过小时迭代次数过多,步长设置过大时,易出现假极值点,步长的选取仍然需要通过信号的质量半经验的选取,整体计算效率不高。相比前3种方法,时间域迭代法及维纳法处理气枪信号时的参数较为固定,对波形的影响相对较小。(2)对于高信噪比的叠加信号,时间域迭代法得到的信噪比最高,相比天然地震信号气枪信号主频带宽较窄且十分固定,反褶积后的窄带滤波能有效改善算法引入高频噪声的缺点,相比在天然地震中的应用,其在气枪信号中的应用更有优势,是一种较好的计算方法。对于单次激发信噪比较低的信号计算结果相对复杂,时间域迭代法得到格林函数信噪比最高,且P,S震相较为清晰,但是波形变形也最为严重,故建议在只需要信号震相到时信息时可以使用时间域迭代法。需波形信息时,最小二乘法和维纳法都可以得到可信度较高的波形,但从计算效率上考虑,维纳法是更加折中的方法。
- 陈佳,叶泵,高琼,等.2017.利用气枪震源信号研究2016年云龙MS5.0地震前后波速变化特征[J].地震研究,40(4):550-556.
- 陈颙,张先康,丘学林,等.2007.陆地人工激发地震波的一种新方法[J].科学通报,52(1):1-5.
- 陈颙,朱日祥.2005.设立“地下明灯研究计划”的建议[J].地球科学进展,20(5):485-489.
- 蒋生淼,王宝善,张云鹏,等.2017.一种基于信号噪声特征的主动源数据自动筛选与叠加方法[J].地震研究,40(4):534-542
- 林建民,王宝善,葛洪魁.2008.大容量气枪震源特性及地震波传播的震相分析[J].地球物理学报,53(2):342-349.
- 王伟涛,王宝善,蒋生淼,等.2017.利用气枪震源探测大陆浅部的地震学研究回顾与展望[J].地震研究,40(4):514-524.
- 吴庆举,田小波,张乃铃,等.2003.用Wiener滤波方法提取台站接收函数[J].中国地震,19(1):41-47.
- 许立生,陈运泰.1996.用经验格林函数方法从长周期数字波形资料中提取共和地震的震源时间函数[J].地震学报,18(2):156-169.
- 杨微,王宝善,葛洪魁,等.2013.大容量气枪震源主动探测技术系统及试验研究[J],中国地震,29(4):399-410.
- 翟秋实,姚华建,王宝善.2016.气枪震源资料反褶积方法与处理流程研究[J].中国地震,32(2):295-304.
- 张云鹏,李孝宾,王伟涛,等.2017.云南宾川地震信号发射台的流动观测数据服务系统及数据质量评估[J].地震研究,40(4):525-533.
- Bell A J,Sejnowski T J.1995.An information-maximization approach to blind separation and blind deconvolution[J].Neural computation,7(6):1129-1159.
- Bostock M G.1998.Mantle stratigraphy and evolution of the Slave province[J].J Geophys Res,103(B9):21183-21200.
- Gurrola H,Baker G E,Minster J B.1995.Simultaneous time-domain deconvolution with application to the computation of receiver functions[J].Geophys J Int,120:537-543.
- Helmberger D,Wiggins R A.1971.Upper mantle structure of midwest United States[J].J Geophys Res,76(14):3229-3245.
- Kiknchi M,Kanamori H.1982.Inversion of complex bodywaves[J].Bul Seism Soc Am,72(2):491-506.
- Lines L R,Treitel S.1984.Tutorial a review of least-squares inversion and its application to geophysical problems[J].Geophys Prosp,32:159-186.
- Menke W.1984.Geophysical data analysis:discrete inverse theory[M].New York:Academic Press.
- Sheehan A F,Abets G A,Leruer-Lam A L,et al.1995.Crustal thickness variation across the Rocky Mountain Front from teleseismic receiver functions[J].J Geophys Res,100(B10),20391-20404.
- Wang B S,Tian Xiao F,Zhang Y P,et al.2018.Seismic Signature of an Untuned Large-Volume Airgun Array Fired in a Water Reservoir[J].Seismological Research Letters,doi:10.1785/0220180007.
- Yang W,Wang B S,Yuan S Y,et al.2018.Temporal Variation of Seismic-Wave Velocity Associated with Groundwater Level Observed by a Downhole Airgun near the Xiaojiang Fault Zone[J].Seismological Research Letters,doi:10.1785/0220170282.