基金项目:中央高校基本科研业务费(ZY20180305)、国家重点研发计划项目(2017YFC1500403)、国家自然科学基金项目(41504043)和北京市自然科学基金项目(8182056)联合资助.
(1.防灾科技学院,河北 三河 065201; 2.中国地震局地壳应力研究所 北京100085; 3.中国地震应急搜救中心工程勘测部,北京 100049)
(1.Institute of Disaster Prevention, Sanhe 065201, Hebei,China)(2.Institute of Crustal Dynamics, China Earthquake Administration, Beijing 100085,China)(3. Engineering Survey Department, National Earthquake Response Support Service, Beijing 100049,China)
horizontal-to-vertical spectral ratio(HVSR); strong earthquake observation; transfer function
备注
基金项目:中央高校基本科研业务费(ZY20180305)、国家重点研发计划项目(2017YFC1500403)、国家自然科学基金项目(41504043)和北京市自然科学基金项目(8182056)联合资助.
采用日本KiK-net台网中9个台站的实测场地模型及多个地震的强震观测记录等数据,对HVSR方法应用于强震数据时“基岩处水平-竖向谱比为1”的假定进行了讨论,并探讨了利用不同系数计算场地水平传递函数TFH的差异,最后对表征不同TFH差异的系数进行了相关性分析。结果 表明:强震观测数据揭示的基岩内水平-竖向谱比不一定为1,仅在某一频率范围内可以视为一个常数; 表征用不同TFH差异的系数C取为1〖JB<1/〗(2αB/βB)1/2时,计算得到的水平向传递函数与实际观测得到的水平向经验传递函数一致性较好; HVSRB与1〖JB<1/〗(2αB/βB)1/2在所考虑的频率范围内存在一定的弱相关性。
Firstly, using the measured data of 9 stations in the Japan KiK-net network and the strong earthquake observation records of several earthquakes, we discussed the assumption that ‘the horizontal-vertical spectral ratio of bedrock is 1' when HVSR method is applied to strong earthquake data. Secondly, on this basis, we calculated the differences between the TFH of the site horizontal transfer function by using different coefficients. Finally, the correlation coefficients of the TFH differences calculated by different formulas are analyzed. The results show that the horizontal-to-vertical spectral ratio in the bedrock revealed by the strong earthquake observation data is not necessarily 1, and can be regarded as a constant only in a certain frequency range. When the coefficient C which is used to estimate the difference of TFH with different formulas is taken as 1/(2αB/βB)1/2, the theoretically calculated horizontal transfer function is in good agreement with the actual observed horizontal transfer function. There is a certain weak correlation between HVSRB and(2αB/βB)1/2 in the frequency range considered.
引言
场地效应一直是地震工程领域研究的热点,表现为地震动作用范围内的地震灾害的地表破坏现象(彭承光,2004)。其主要是由地震波经过不同场地条件时对地震动的放大导致的,直接影响地震灾害程度的分布(李小军,彭青,2001)。目前,有许多基于地震动记录的经验分析方法被广泛用于场地效应的研究,包括传统谱比法(Borcherdt,1970),线性反演法(Andrews,1986)和水平-垂直谱比法(Horizontal to Vertical Spectra Ratio,简称HVSR)(Nakamura,1989)。其中,HVSR谱比法因不受参考场地的约束而被广泛应用。
HVSR谱比法由Nakamura(1989)提出,是一种基于同一地表测点地脉动水平向和竖向分量傅里叶幅值谱比值估计场地动态特征的方法。在大量地脉动观测的基础上,Nakamura(1989)曾提出2个基本假定:①地震波由基岩传播至地表后,竖向分量基本不放大,竖向传递函数为1; ②基岩处的HVSR谱比为1,即HVSRB=1。
若上述假定均成立,则容易推知ETFH=HVSRS,即地表处的HVSR谱比可直接视为水平向经验传递函数。这就意味着只需利用单台三分量的地表观测记录就可获得水平向经验传递函数,进而估计场地放大效应。HVSR谱比法最早是基于地脉动进行场地动力特性研究的,经过几十年的发展,该方法已扩展至基于强震动研究场地动力特性的领域。因这一方法的简便性,国内外许多学者将该方法应用于场地效应研究(王伟君等,2009; Xu et al,2013)。但这一方法的基本假定是否成立仍存在较大的争议(卢滔等,2006),Javier等(1994)通过不同的方法对HVSR谱比法的基本假定进行了验证,但所得结论不一,Victor等(2002)认为基岩处HVSR谱比为1或接近1,但还有人认为其值为某一常数。
本文以日本KiK-net台网中的9个台站获取的地震动记录为基础数据,对各台站的场地土层数据和傅里叶幅值HVSR谱比进行统计分析,讨论HVSR方法应用于强震数据时的第2个假定的合理性,并给出相关建议。
1 数据选取
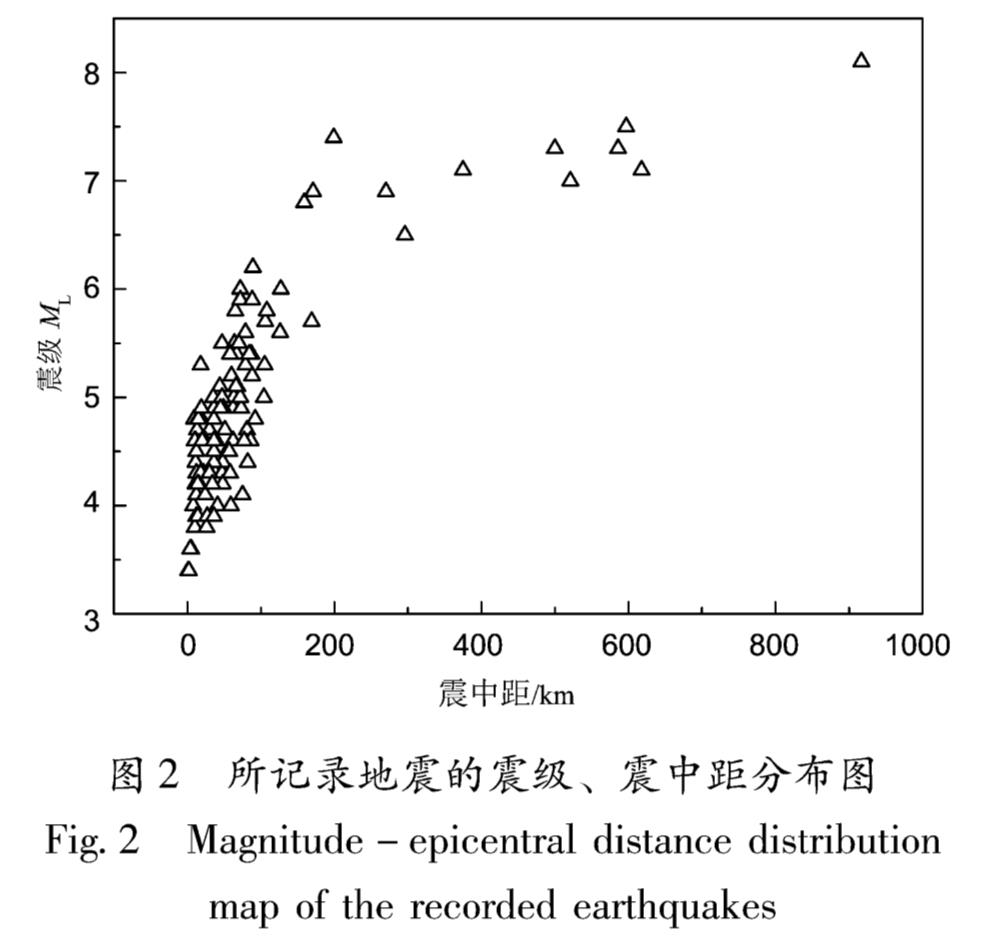
KiK-net台网是为研究地下强震动传到地表的变化而建设的井下强震观测系统,由689个地表和井下三分量数字加速度仪台站组成,在地表和井下分别安装了较高灵敏度的加速度计,仪器采样频率是200 Hz,仪器动态范围120 dB,满量程±2 g,仪器触发阈值是0.2 gal,最小记录长度是120 s(史大成等,2011)。Thompson等(2012)提出: 当各个地震事件获得的经验传递函数的差异和各个台站地震数据获得的经验传递函数与一维理论传递函数的差异均较小时,可认为该台站场地能用一维土层模型近似描述。本文依据上述标准从KiK-net台网中选取了符合一维场地假设,并且可以认为没有二维和三维地形影响的9个台站, 分别为TKCH08,FKSH11,FKSH14,IWTH27,IBRH10,IWTH08,IBRH13,IBRH17和KSRH10台,各台站速度剖面和钻孔柱状图及基岩处传感器深度位置如图1所示(方括号内数字为剪切波速值; 圆括号内数字为对应土层P波波速值),9个台站中钻孔底部最浅深度为100 m,最深为900 m。本文依据地震动峰值加速度PGA介于30~50 gal的筛选原则选取了从2011年3月11日至2017年12月16日记录到的共110条地震动记录,如图2所示,其中PGA范围为30.1~49.9 gal,震级范围为ML3.4~8.1,震源深度范围为6~682 km,震中距范围为1~917 km,详见表1。
2 数据处理与统计分析
计算与处理HVSR谱比曲线共3个步骤:①对
9个台站记录到的共110条地震动记录进行带通滤波和基线校正处理,带通滤波用于消除关注范围外的频率成分,基线校正是校正因低频误差和地震动导致仪器倾斜引起的基线漂移(王德才,叶献国,2011)。本文所用数据均采用巴特沃斯带通滤波器进行带宽为0.1~25 Hz的滤波处理; ②计算所有记录地表和基岩处三分量的傅里叶幅值谱,并使用Konno和Ohmachi(1998)提出的平滑方法对傅里叶幅值谱进行平滑; ③利用HVSR谱法计算出水平向与竖向分量的几何平均谱比。图3分别给出了9个台站在基岩处NS向、EW向和合成的水平分量HVSRB谱比曲线。
由图3可以看出,依据9个台站的地震动记录给出的NS向、EW向及合成的水平分量HVSRB谱比曲线在0.1~25 Hz均值变化不大,可以近似看作一个常数,各台站谱比曲线的大部分位于HVSRB=1水平线之上,并不能直接近似为“1”,其中,谱比曲线峰值的最大值在NS向为IBRH17台站
图3 9个台站NS方向、EW方向和合成的水平分量HVSRB谱比曲线
Fig.3 HVSR spectral ratio curves in NS and EW directions and synthetic horizontal component at base rocks of 9 stations(4.90),在EW向为FKSH11台站(4.62),合成的水平分量为FKSH11台站(6.32)。对各台站基岩处单分量与合成的水平分量谱比曲线的均值取平均,可以看出,虽然这9个台站的谱比曲线均值在1~2,但在该频段内并非为一个固定不变的数值,而是与HVSRB相关的常数,并不适用于HVSR方法的第二个假定:HVSRB=1。卢滔等(2006)也证实了该方法的这一假定在地震作用下不成立,仅在地脉动作用下符合基岩谱比为1的假定。
3 HVSRB的取值讨论
本文定义自由地表水平向、竖向分量的傅里叶幅值谱分别为HS(f)和VS(f); 基岩处水平向、竖向分量的傅里叶幅值谱分别为HB(f)和VB(f); H代表水平方向、V代表竖直方向; S代表自由地表、B代表井下基岩。根据传递函数定义可知,任意水平向的传递函数可以表示为:
ETFH=(HS(f))/(HB(f))(1)
经变换可得:
ETFH=(HS(f))/(VS(f))×(VS(f))/(VB(f))×(VB(f))/(HB(f))(2)
即:
ETFH=HVSRS×ETFV×1/(HVSRB)(3)
式中:HVSRS和HVSRB分别为地表处和井下基岩处的水平与竖向分量的傅里叶幅值谱比; ETFH和ETFV分别为水平向和竖向的经验传递函数,因HB(f)和VB(f)是基岩处地震动的分量,所以会包含有上行波和下行波的影响,因此只有当下行波的影响可以被忽略时,ETF才可以被认为是TF。
有研究表明地表处的HVSRS与TFH均能给出足够相似的卓越频率值(Satoh et al,2001),但是二者之间的傅里叶谱比幅值相差较大(Rong et al,2017),由式(3)可以看出其主要受到竖向传递函数TFV和基岩处的HVSRB的影响。还有相关研究指出:引起水平向传递函数TFH和地表处HVSRS差异的主要原因是TFV不为1(卢滔等,2006; 荣棉水等,2016),因此在下文中的TFV将通过实际记录计算给出。
如果采用Nakamura(1989)提出的方法中基岩处的HVSRB=1的假定,则依据式(3)得到的水平向传递函数TFH将与实际TFH相差较大,并不能应用于实际工程。下文中将探讨HVSRB取不同的值时计算得到的水平传递函数与实际水平传递函数间的差异。
在假定基岩处地震动分量不受下行波的影响后,ETFH可以改写成TFH,ETFV可以改写成TFV,故式(3)可以写成:
TFH=HVSRS×TFV×1/(HVSRB)(4)
式中:TFH和TFV分别为水平向和竖向传递函数。
Herak(2008)提出利用S波和P波的放大谱比来计算HVSR,并假设地震波为垂直入射的体波,则S波的传递函数AMPS(f)和 P波的传递函数AMPP(f)可分别表示为TFH和TFV,则得:
TFH=HVSRS×TFV×1(5)
但Herak(2008)在研究中应用的计算数据来自于环境噪声,并未考虑上式在地震动作用下的适用性。Kawase等(2011)基于扩散场理论提出了一个计算理论HVSR的公式,如下:
HVSR=((2αB)/(βB))1/2(〖JB<1|〗TFS(h,ω)〖JB>1|〗)/(〖JB<1|〗TFP(h,ω)〖JB>1|〗)(6)
式中:TFS(h,ω)和TFP(h,ω)分别为井下深度h处S波和P波的传递函数; αB和βB分别为基岩处P波和S波波速。在地震波为垂直入射的体波的假设下,TFS(h,ω)和TFP(h,ω)分别表示为地震动水平向传递函数TFH和竖向分量传递函数TFV,因此式(6)可写成如下格式:
TFH=HVSRS×TFV×1/((2αBβB)1/2)(7)
对比式(4),(5)和(7),可以看出不同的研究人员给出了非常相似的理论HVSR公式,上述3个公式可以用一个统一的公式来表示:
TFH=HVSRS×TFV×C(8)
式中:C在Herak(2008)中被假定为常数1,这与Nakamura(1989)提出的基本假定一致,即基岩处的水平向与竖向分量是相等的; 而在Kawase等(2011)的研究中,C被认为是与基岩的P波和S波速度有关的常数; 在本文以及Rong等(2017)的研究中,C被认为是基岩处的HVAR谱比曲线,并非一个固定的常数。
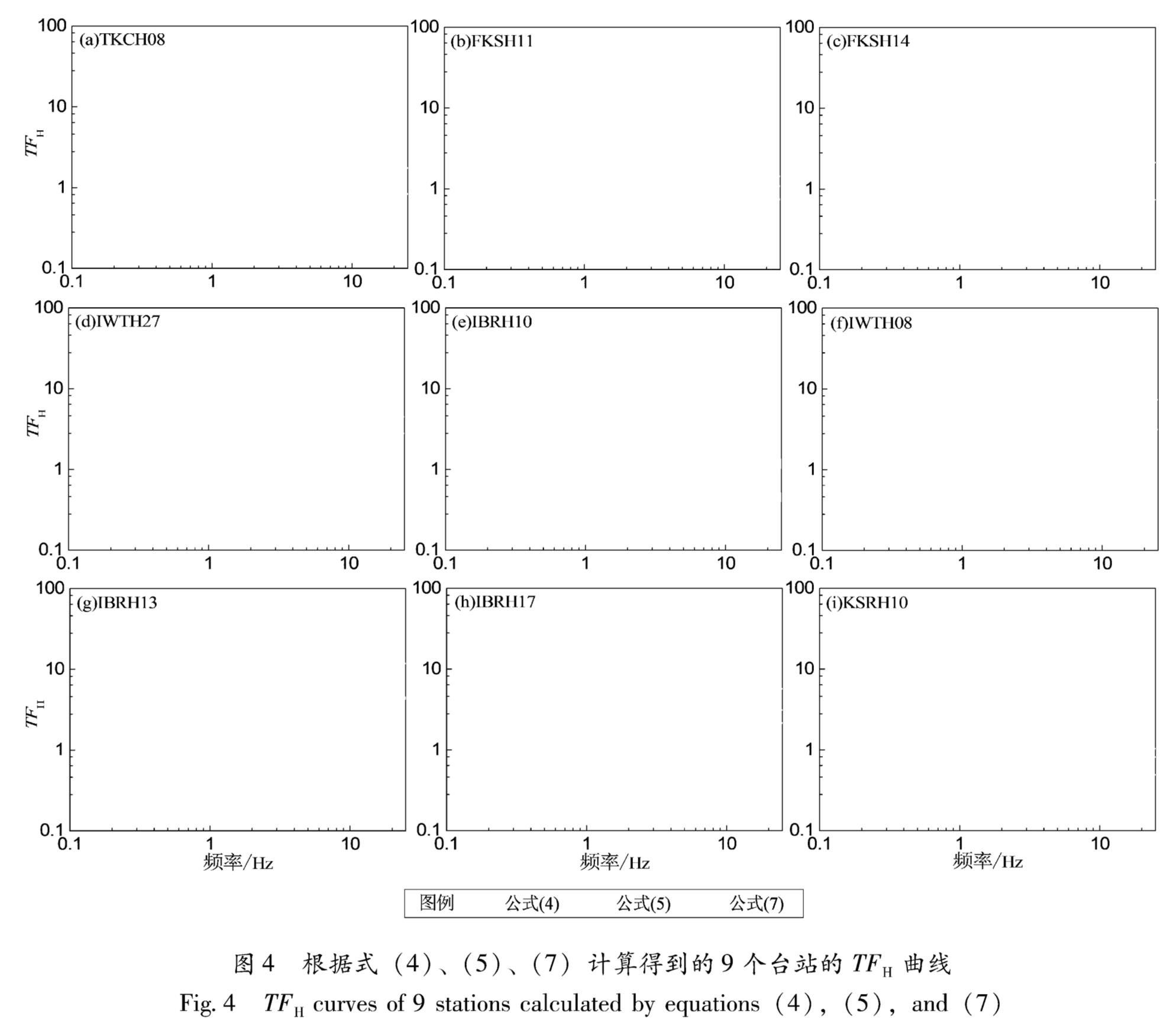
为了给出较合理且准确的水平向传递函数TFH,比较上述不同的系数C计算出的不同TFH,以判断系数C取值性的合理。图4给出了分别根据公式(4)、(5)和(7)计算出的TFH曲线。
图4 根据式(4)、(5)、(7)计算得到的9个台站的TFH曲线
Fig.4 TFH curves of 9 stations calculated by equations(4),(5),and(7)由图4可以看出,3个公式计算出的传递函数曲线,均表现出较为相似的谱形,其中式(4)计算出的水平传递函数即为观测的经验传递函数; 式(5)和式(7)的曲线谱形一致,但幅值不同,式(4)和式(7)的曲线谱型较为相似,幅值也相差较小,表现出很好的一致性,和Rong等(2017)得出的结果一致; 式(5)计算出的曲线的幅值均大于式(4),但是每条曲线峰值处对应的卓越频率相差甚小。可以看出,不论系数C如何取值,对获取卓越频率的准确性的影响可不予考虑,但对曲线幅值的影响不可忽略。
4 对合成的水平分量HVSRB和(2αBβB)1/2相关性的探讨
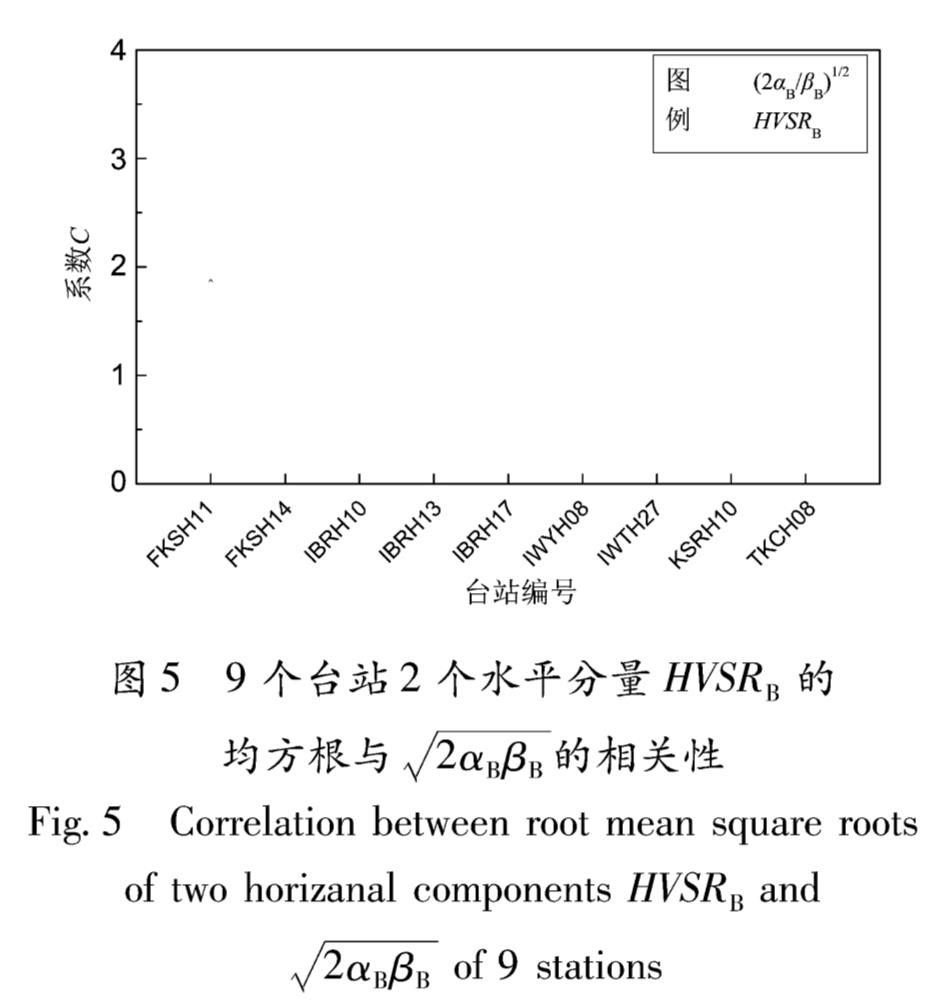
卢滔等(2006)、荣棉水等(2016)应用传递函数TF来估计场地放大在国内外都是被广泛接受的,表明导致TFH与HVSRH差异的主要原因是TFV不符合Nakamura方法的基本假定,而在本文中TFV是由实际记录计算给出的,因此,在不考虑HVSRB=1的情况下,根据式(4),(5)和(7)可以知道影响TFH的另一个因素是系数C的取值。在图4中可以看出当利用公式(7)计算时的传递函数曲线与实际记录计算得到的曲线更接近。图5给出了9个台站合成的水平分量HVSRB与(2αBβB)1/2的相关性,其中合成的水平分量HVSRB是取自每个台站基岩处HVSR谱比的平均值。
从图5可以看出,9个台站的系数C均在1.5~3内,且所有台站中(2αBβB)1/2均大于合成的水平分量HVSRB平均值,其中IWTH08台站2个C值相差最大为1.12,FKSH11台站2个C值相差最小为0.1,由于分析的台站数量较少,相关性并不是很明显,但是根据其差值大小可以粗略判断出在所考虑的频率范围内2个系数C之间仍存在相关性。通过下式可以计算出2个系数C之间的皮尔逊相关系数为0.54:
r=(N∑Ni=1xiyi-∑Nixi∑Niyi)/((N∑Ni=1x2i-(∑Nixi)2)1/2-(N∑Ni=1y2i-(∑Niyi)2)1/2)(9)
图5 9个台站2个水平分量HVSRB的均方根与(2αBβB)1/2的相关性
Fig.5 Correlation between root mean square roots of two horizanal components HVSRB and (2αBβB)1/2 of 9 stations5 结论
本文选取日本KiK-net台网中9个符合一维场地假设的台站的场地数据和记录到的110条地震动记录为基础数据,通过统计分析讨论了HVSR方法中的一个假定,并通过对比选取不同的C值计算出的水平传递函数,探讨了不同C值下水平传递函数间的差异,还对2个不同的C值进行了相关性分析。得到如下结论:
(1)在地震动作用下,HVSR方法关于“基岩处水平与竖向傅里叶幅值谱比为1”的假定不成立,但在某一频率范围内,可以被认为是一个常数。
(2)在下行波可以被忽略的假设下,可以通过3种公式计算出水平传递函数TFH,并可以利用统一公式:TFH=HVSRS×TFV×C来表示,其中系数C表征着幅值差异。
(3)当系数C=1〖JB<1/〗(2αBβB)1/2时,即与基岩处的波速特征相关时,得出的水平传递函数曲线与实际的水平传递函数曲线更为一致。
(4)基岩处水平-垂直谱比HVSRB与(2αBβB)1/2在本文所考虑的频段内存在着一定的相关性,但可能因数据量较少,分析已有数据并未揭示明显的相关性,皮尔逊相关系数仅为0.54。
- 李小军,彭青.2001不同类别场地地震动参数的计算分析[J].地震工程与工程振动,21(1):29-36.
- 卢滔,周正华,周雍年,等.2006.关于Nakamura方法有效性的讨论[J].地震工程与工程振动,26(1):43-48.
- 彭承光.2004.场地地震效应工程勘察基础[M].北京:地震出版社.
- 荣棉水,李小军,王振明,等.2016.HVSR方法用于地震作用下场地效应分析的适用性[J].地球物理学报,59(8):2878-2891.
- 史大成,温瑞智,任叶飞.2011.基于GIS的场地分类方法研究[J].地理信息世界,9(1):23-27.
- 王德才,叶献国.2011.近断层强震记录基线校正及不确定性分析[J].世界地震工程,27(2):63-69.
- 王伟君,刘澜波,陈棋福,等.2009.应用微动H/V谱比法和台阵技术探测场地响应和浅层速度结构[J].地球物理学报,52(6):1515-1525.
- Andrews D J.1986.Objective determination of source parameters and similarity of earthquakes of different size[J].Earthquake Source Mechanics,37:259-267.
- Borcherdt R D.1970.Effects of local geology on ground motion near San Francisco Bay[J].Bull Seismol Soc Am,60(1):29-61.
- Herak M.2008.Model HVSR—AMatlab tool to model horizontal-to-vertical spectral ratio of ambient noise[J].Comput Geosci,34:1514-1526.
- Javier Lermo,Francisco J,Chavez Garcial. 1994.Are microtremors useful in site response evaluation?[J]. Bulletin of the Seismological Society of America,84(5):1350-1364.
- Kawase H,Sánchez-Sesma F J,Matsushima S.2011.The optimal use of horizontal-to-vertical spectral ratios of earthquake motions for velocity inversions based on diffuse-field theory for plane waves[J].Bull Seismol Soc Am,101(5):2001-2014.
- Konno K,Ohmachi T.1998.Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor[J].Bull Seismol Soc Am,88(1):228-241.
- Nakamura Y.1989.A method for dynamic characteristics estimation of subsurface using microtremor on ground surface[J].Q Rep Railway Tech Res Inst,30(1):25-33.
- Rong M S,Li Y F,Li X J.2017.On the amplitude discrepancy of HVSR and site amplification from strong-motion observations[J].Bulletin of the Seismological Society of America,107(6):2873-2884.
- Satoh T,Kawase H,Matsushima S.2001.Differences between site characteristics obtained from microtremors,S-waves,P-waves,and codas[J].Bull Seismol Soc Am,91(2):313-334.
- Thompson E M,Baise L G,Tanaka Y,et al.2012.A taxonomy of site response complexity[J].Soil Dynamics and Earthquake Engineering,41:32-43.
- Xu P F,Ling S Q,Ran W Y,et al.2013.Estimating cenozoie thickness in the Beijing plain area using array microtremor data[J].Seismological Research Letters,84(6):1039-1047.
- Victor H S,Rodriguez,Saburoh Midorikawa. 2002.Applicability of the H/V spectral ratio of microtremors in assessing site effects on seismic motion[J]. Earthquake Engineering & Structural Dynamics,31(2):261-279.