基金项目:国家自然科学基金项目(51678540,51478443和51178435)资助.
(中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080)
(Key Laboratory of Earthquake Engineering and Engineering Vibration,Institute of Engineering Mechanics,China Earthquake Administration,Harbin,150080, Heilongjiang,China)
sensitivity analysis; site amplification factor; random shear velocity model; quarter-wavelength method; transfer function
备注
基金项目:国家自然科学基金项目(51678540,51478443和51178435)资助.
以Turkey Flat标准试验场为基准场地,以Toro剪切波速模型为基础,进行Monte Carlo模拟,生成剪切波速、层厚和密度随机样本各200条,将各土层随机参数组成4个工况作为不确定分析的基础。采用常用的四分之一波长法和传递函数法计算场地放大因子,分析放大因子以及特征周期对4种工况的敏感度。结果 表明:土层剪切波速、层厚和密度的随机性对2种方法计算得到场地放大因子有相同的影响; 剪切波速的随机性对放大因子和特征频率的影响比其他参数大; 四分之一波长法得到的放大因子和特征频率对土层各参数的敏感性弱于传递函数方法。
According to the Toro share velocity model,we use the Monte Carlo method to generate 200 shear velocities,thickness and density random samples for uncertainty analysis,based on soil structure from the Turkey Flat site.Computing the quarter-wavelength(QWL)method amplification factor as well as transfer function(TF)and estimating their sensitivity under four conditions made up of random soil samples mentioned above.The results show that uncertainties of shear velocity,thickness and density have same impact on the spectrum characteristics using two methods.The influence of shear velocity on both amplification factors and fundamental frequency is predominant among different soil parameters.In addition,amplification factors and fundamental frequency of QWL are less sensitive to random soil parameters than that of TF's.
引言
在地震工程中,局部地质条件和岩土力学性质的差异影响着地震动的幅值、频谱和持时。考虑场地效应时,可以使用基于实测地震动记录的谱比法和基于土层钻孔数据的理论分析法。进行场地地震反应分析时会存在较大的不确定性,包括:场地模型的不确定性、地震动输入的不确定性以及数值计算模型的不确定性等。
本文主要讨论场地模型的不确定性,其中土层参数包括剪切波速、土层厚度和土层密度。这些不确定性主要来源2方面:同类场地在不同地区的土层参数分布具有离散性; 在同一场地对土层参数的测量误差(陈龙伟等,2014)。Toro(1993)调查了全球411个场地土层结构得到剪切波速和土层厚度的统计特征,并指出剪切波速呈对数正态分布。
已有研究多数以传递函数或基于传递函数的等效线性法来估计场地模型的不确定性反应,一般结论为剪切波速相对于其它土层参数对传递函数影响最大。而关于四分之一波长法的场地放大因子还没有相关研究,该方法被广泛应用于计算高频地震动的场地反应,所用场地模型是同一分类或者同一区域的场地拟合所得土层结构。本文以传递函数作为参考,考虑剪切波速、厚度和密度的随机性对四分之一波长法放大因子的影响,同时比较传递函数法和四分之一波长法这2种方法对土层参数随机性的敏感度。
1 研究方法
Joyner等(1981)提出四分之一波长法,它是一种计算频率相关场地效应的简化方法。该方法可以忽略一些深度的土层结构从而计算随机合成地震动中的场地项,假设不考虑波在土层中传播的反射、散射和衰减,波的能量恒定且幅值与土层波阻抗的平方根成反比。Day(1996)用宽带入射波的传递函数均方根反应推导出了单均匀层的四分之一波长法。Boore和 Joyner(1997)提出相对应场地模型结合高频衰减因子计算出场地放大因子,并被广泛应用于高频地震动模拟的场地计算,关系式如下:
A[f(z)]=((ρbVb)/(ρ^-(z)V^-(z)))1/2(1)
式中:Vb和ρb分别为基岩处的剪切波速和密度; V^-(z)和ρ^-(z)分别表示深度为z时土层的平均剪切波速与平均密度:
V^-(z)=z/∫z01/(V(ξ))dξ(2)
ρ^-(z)=1/z∫z0ρ(ξ)dξ(3)
f(z)为不同深度对应的频率,其计算公式为:
f(z)=1/(4Stt(t))(4)
式中:Stt(t)为剪切波从覆盖层深度z到地表的传播时间,具体计算公式为:
Stt(t)=∫z01/V(ξ)dξ(5)
传递函数法则是由波动方程结合边界条件推出,表示一个线性土层系统内,基岩输入和地表反应的函数关系,同时能够反映土层的场地卓越周期等固有性质。对比传递函数,四分之一波长法相对简单,并且计算的场地放大因子偏低(Boore,2013)。在本文中,2种方法都仅在线弹性范围内计算,没有考虑土体在动力反应下的阻尼衰减和土体的非线性性质。
2 土层随机模型
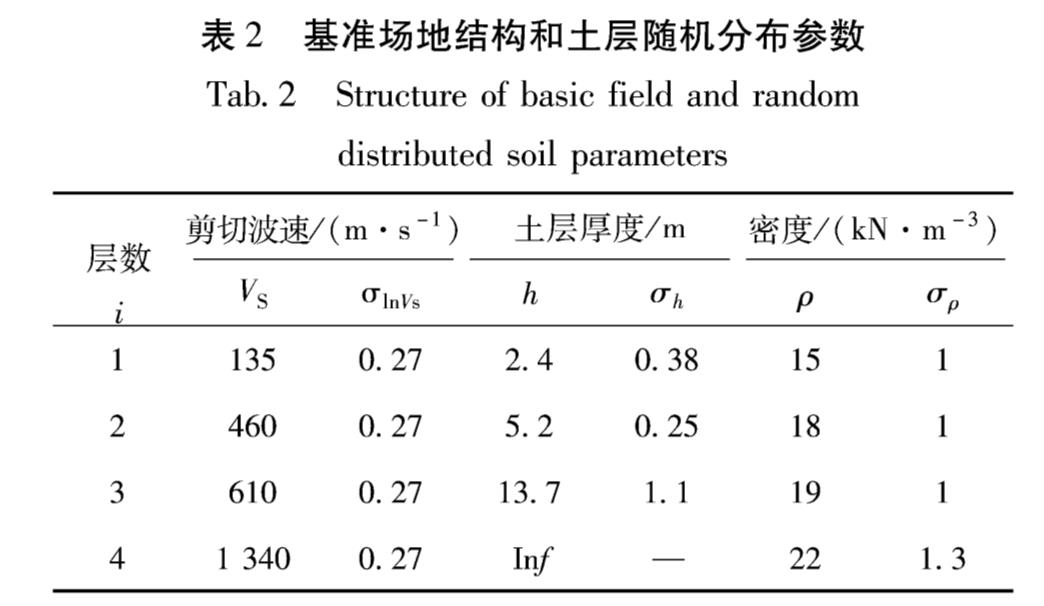
Turkey Flat场地位于美国加州洛杉矶和旧金山之间的Parkfield地区,是一个处于浅硬泥土冲积河谷中的标准试验场地。1986—1987年修建了2个垂直台阵并且在钻孔内安置了加速度传感器,一个位于Rock South,深25 m; 另一个位于Valley Center,深40 m(Real,1988)。本文将Valley Center钻孔数据(Real,1988)作为Monte Carlo法模拟随机场地结构的基准场地,钻孔数据如表2所示。基准场地30 m土层的平均剪切波速VS30为757.7 m/s,根据美国国家地震减灾计划(NEHRP)该场地分类为C类,属于较硬岩石场地。
随机剪切波速采用Toro1995统计模型由基准场地结构生成,Toro(1993,1995)认为土层的剪切波速在给定深度服从对数正态分布并给出剪切波速的统计模型,他调查超过557个剪切波速结构,对该模型做出一些调整。根据调整后的模型,第i层随机剪切波速VS(i)可以由基准场地第i层剪切波速VS,O(i)、剪切波速自然对数标准差σlnVs和第i层正态随机变量Zi求得:
VS(i)=exp{ln[VS,O(i)]+Zi·σlnVs}(6)
McGuire等(1989)假设每一层正态随机变量Z都是完全相关,所以每层乘以相同的Z生成随机剪切波速,而Costantino等(1991)假设Zi相对于每层是独立的。Toro(1995)认为2类假设相比较真实场地有些极端并且不严谨,根据其模型Zi有如下定义:
Z1=ε1(7)
Zi=ρIL·Zi-1+εi·(1-ρ2IL)1/2 i>1(8)
式中:随机变量ε服从标准正态分布,其均值和标准差分别为0和1; ρIL层间相关系数有如下定义:
ρIL(d,h)=[1-ρd(d)]ρh(h)+ρd(d)(9)
式中:d为土层深度; h为土层厚度; 深度相关系数ρd(d)和层厚相关系数ρh(h)定义为:
ρd(d)=ρ200[(d+d0)/(200+d0)]b(d≤200 m)(10)
ρd(d)=ρ200(d>200 m)(11)
ρh(h)=ρ0exp((-h)/(Δ))(12)
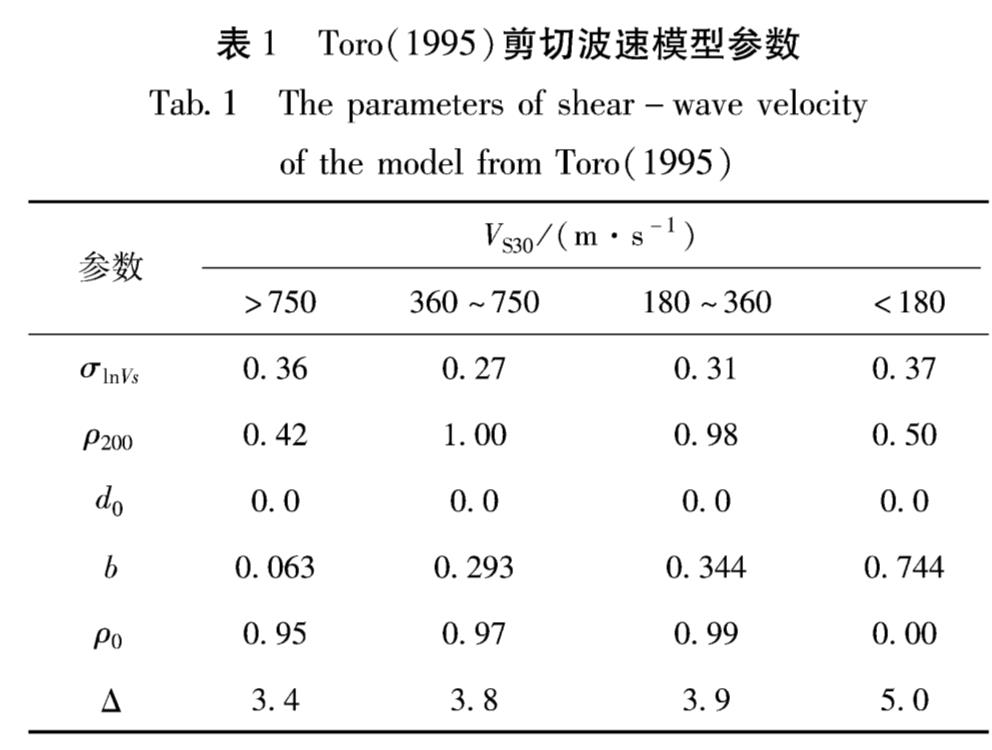
式中:σlnVs=0.27; ρ200=1; d0=0、b=0.293; ρ0=0.97; Δ=3.8,可根据基准场地VS30分类在表1中查得(Rathje et al,2010)。
假设层厚服从正态分布,并且参考Field和Jacob(1993)给出的Valley Center场地随机层厚的标准差,假设随机密度服从对数正态分布(Barani et al,2013)。表2为基准场地结构中剪切波速、层厚和密度以及剪切波速自然对数标准差、层厚的标准差和密度的标准差。随机剪切波速、层厚和密度均以基准场地数据为平均值结合对应的统计特征生成。
对数正态分布参数(洪华生,邓汉忠,2017)由下式计算:
μlnRV=ln((μRV)/((1+(σ2RV)/(μ2RV))1/2))(13)
σlnRV=(ln(1+(σ2RV)/(μ2RV)))1/2(14)
式中: μlnRV和σlnRV是随机变量(如密度)取自然对数后的平均值和标准差; μRV和σRV是随机变量的平均值和标准差(如表2中的随机参数)。
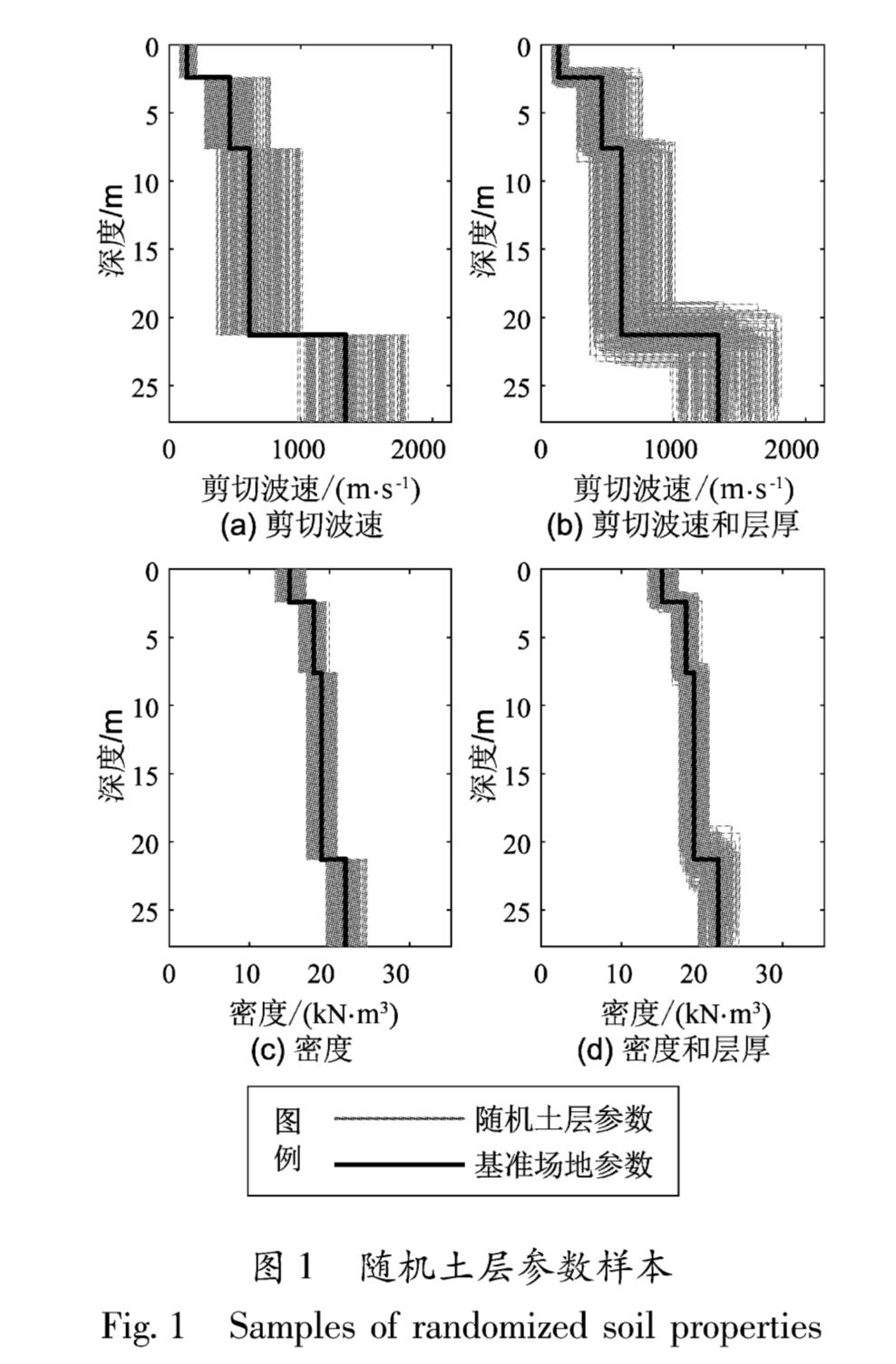
采用Monte Carlo方法结合统计模型生成剪切波速、密度和层厚样本。本文验算过样本数量分别为50,100,200,500,1000时的情形,发现样本数量为200时刚好能合适地表达土层参数的统计模型。图1为随机土层参数样本。值得注意的是,为了避免随机模拟产生不合理的土层参数值,剪切波速、密度和层厚均采用±2σ的截断分布(Bazzurro,Cornell,2004)。
3 分析和结果
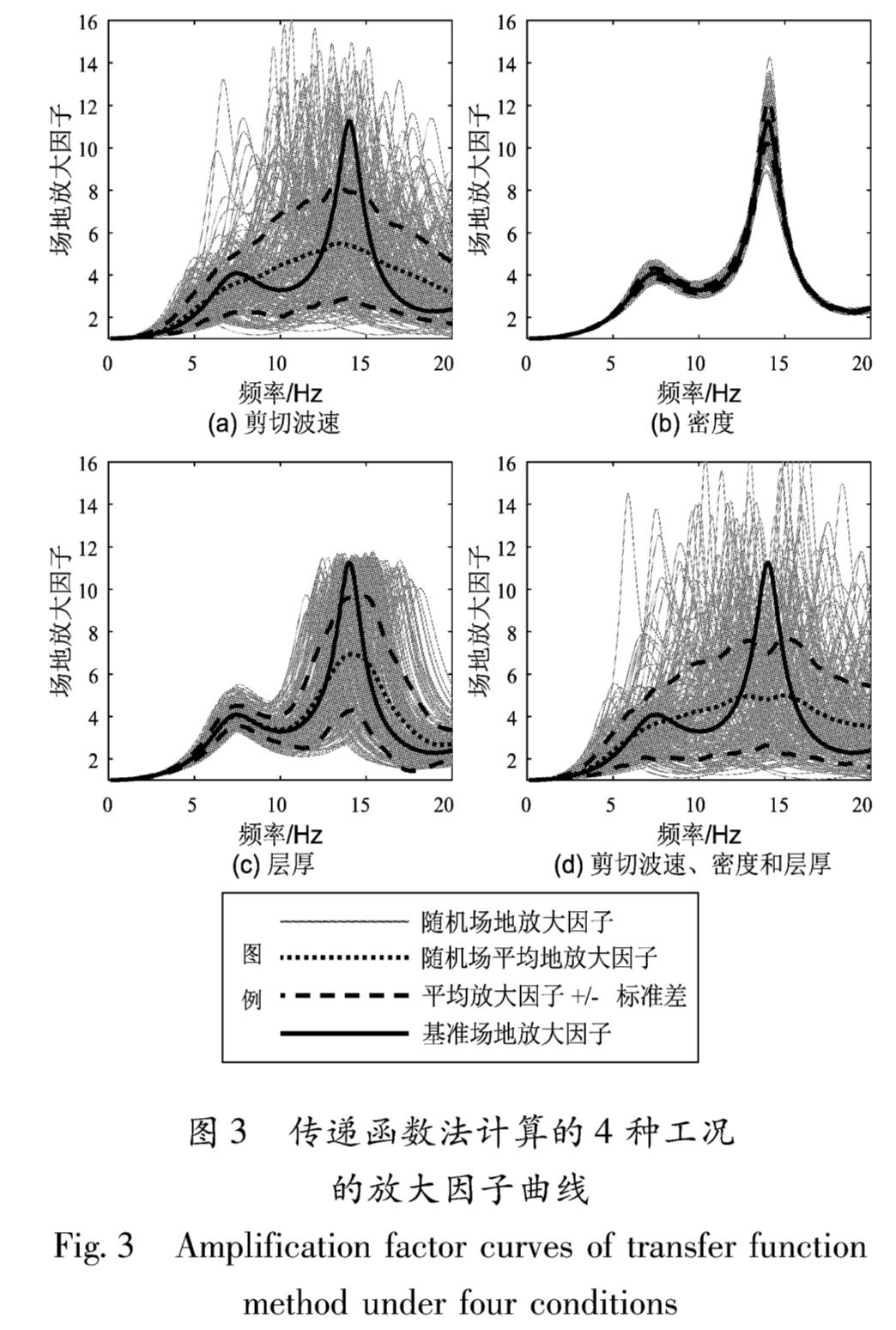
使用已生成的随机土层参数样本,参考刘红帅等(2005)的研究,考虑4种工况作为输入:仅考虑剪切波速的随机性; 仅考虑密度的随机性; 仅考虑层厚的随机性; 同时考虑剪切波速、密度和层厚的随机性。在线弹性范围内,分别利用四分之一波长法与传递函数法计算4种工况各200条随机场地和基准场地的放大因子谱(图2,3),讨论不同随机土层参数对二者的频谱影响,并比较二者对随机土层参数的敏感性。
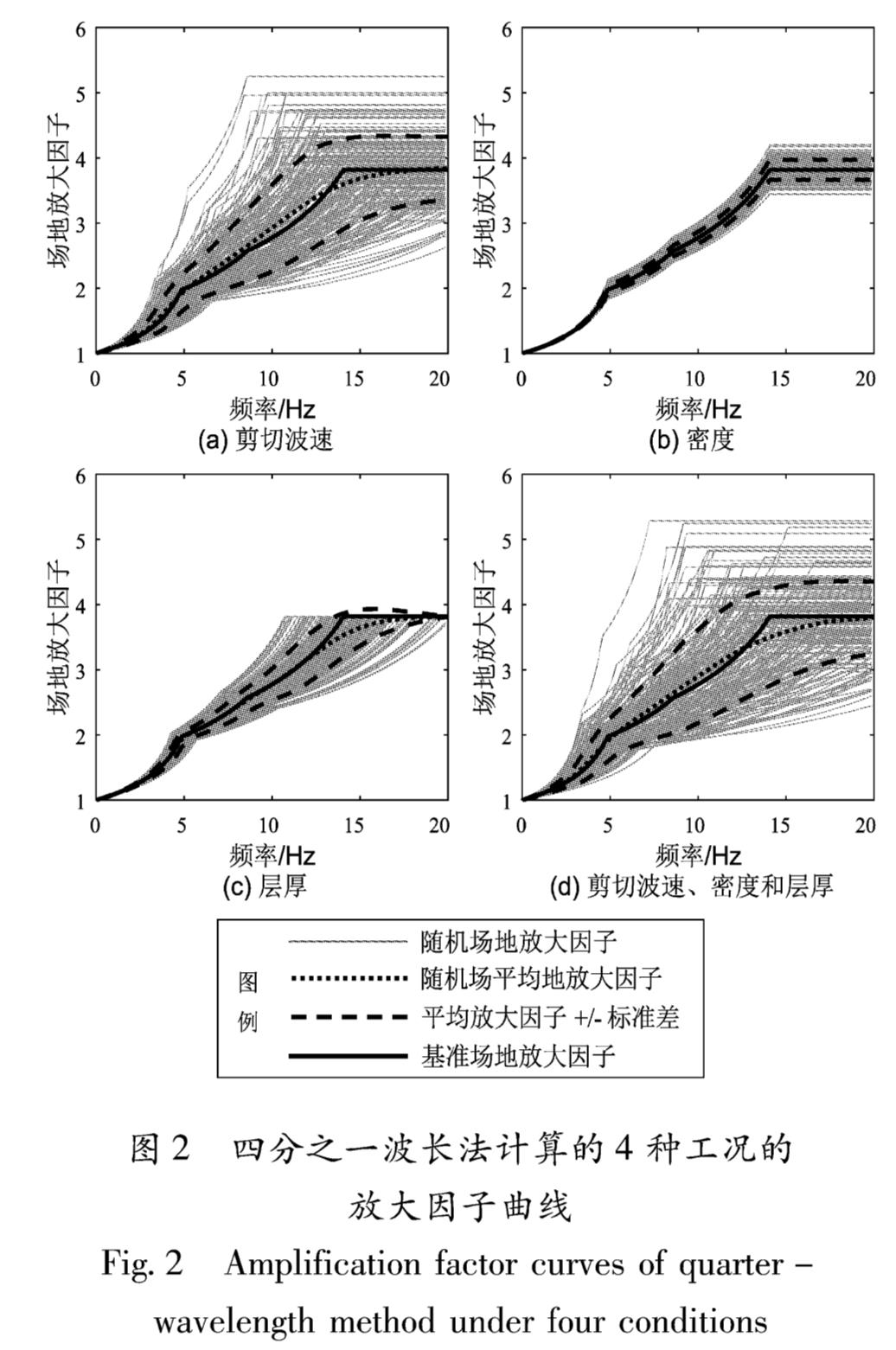
3.1 4种工况对2类方法频谱的影响图2所示四分之一波长法计算的4种工况的放大因子曲线呈现4段并且有3个拐点,拐点可以表示各土层分界面处深度的等效放大作用。在各个工况中,剪切波速同时影响曲线拐点的幅值和频率,而且剪切波速的随机性对四分之一波长法的放大因子影响最大并且与组合工况4相当,放大因子的不确定性随着频率增加而增大然后保持稳定。
由图2,3可以看出,2种方法计算4种工况时,剪切波速对放大因子曲线的影响最大。而对比图2a和图3a发现,剪切波速的随机性对四分之一波长法计算的放大因子的影响比传递函数法小,而且四分之一波长法放大因子曲线相对平滑没有波峰和波谷,这是因为该方法假设波在上层介质没有反射。由图2还可见,相比其它3种工况,密度的随机
图2 四分之一波长法计算的4种工况的放大因子曲线
Fig.2 Amplification factor curves of quarter-wavelength method under four conditions性对四分之一波长法计算的放大因子曲线影响最小,对拐点只有幅值而没有频率范围的影响,这是因为四分之一波长法频率计算式(4)只与深度和剪切波速有关,在传递函数法中同样如此(图3)。二者不同的是当频率大于14 Hz时,传递函数法计算的幅值离散度变小,而四分之一波长法计算的幅值的离散度基本保持不变。
由图2c可知,层厚的随机性造成四分之一波长法计算的放大因子曲线在频率10 Hz以上呈现较大的离散,而且各个拐点的幅值连线几乎和水平轴平行,即幅值的离散性很小,在传递函数法中同样如此(图3c)。综上,在各个工况中剪切波速的随机性对场地放大因子的影响最大,其次是层厚和密度。剪切波速和层厚都会影响放大因子曲线的幅值和峰值(拐点)频率,其中层厚对幅值和峰值(拐点)频率的影响在频率上是有所不同; 密度主要影响放大因子曲线的幅值。值得注意的是,四分之一波长法虽然在幅值与曲线形式上和传递函数法有所差别,但各工况对二者频谱的影响大致相同。
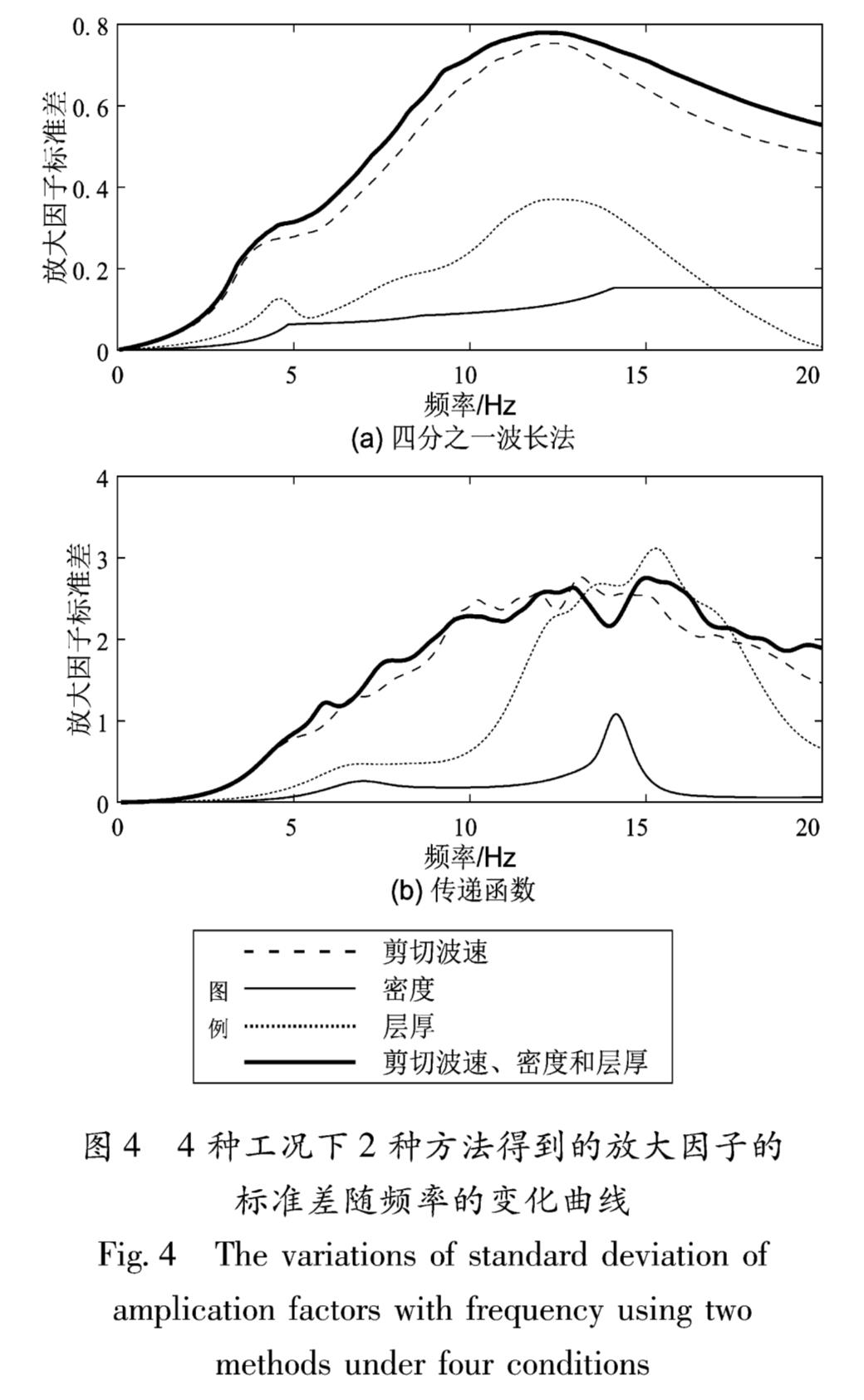
3.2 2种方法对各随机土层参数的敏感性为了比较2种方法得到的放大因子对各个土层随机参数的敏感性,计算4种工况下2种方法得到的放大因子随频率变化的标准差。由图4可见,四分之一波长法对各种土层参数敏感性要比传递函数法小,并且相同工况中二者放大因子的标准差相差3倍多。剪切波速工况产生的标准差和总标准差曲线大致一样,先随频率增加而增大然后频率达到12 Hz左右开始缓慢减少。层厚工况造成二者的标准差随频率先增加后减小,但在10 Hz处,层厚工况下,传递函数法放大因子的标准差增幅明显大于四分之一波长法,且传递函数法的标准差峰值甚至超过了其总标准差。密度工况对二者的标准差呈现出和基准场地放大曲线相同的趋势,在同频率处也有拐点和波峰。
值得注意的是,尽管计算总标准差时考虑了剪切波速、层厚和密度的随机性,但是总标准差在整个频段内与剪切波速的标准差仍旧大体相当,可见2类方法的放大因子对剪切波速的敏感度在各土层
图4 4种工况下2种方法得到的放大因子的标准差随频率的变化曲线
Fig.4 The variations of standard deviation of amplication factors with frequency using two methods under four conditions参数占主导作用,且四分之一波长法对各个土层参数的敏感度远小于传递函数法,总体上,2类方法的放大因子对各土层参数的敏感度高频段比低频段更高。
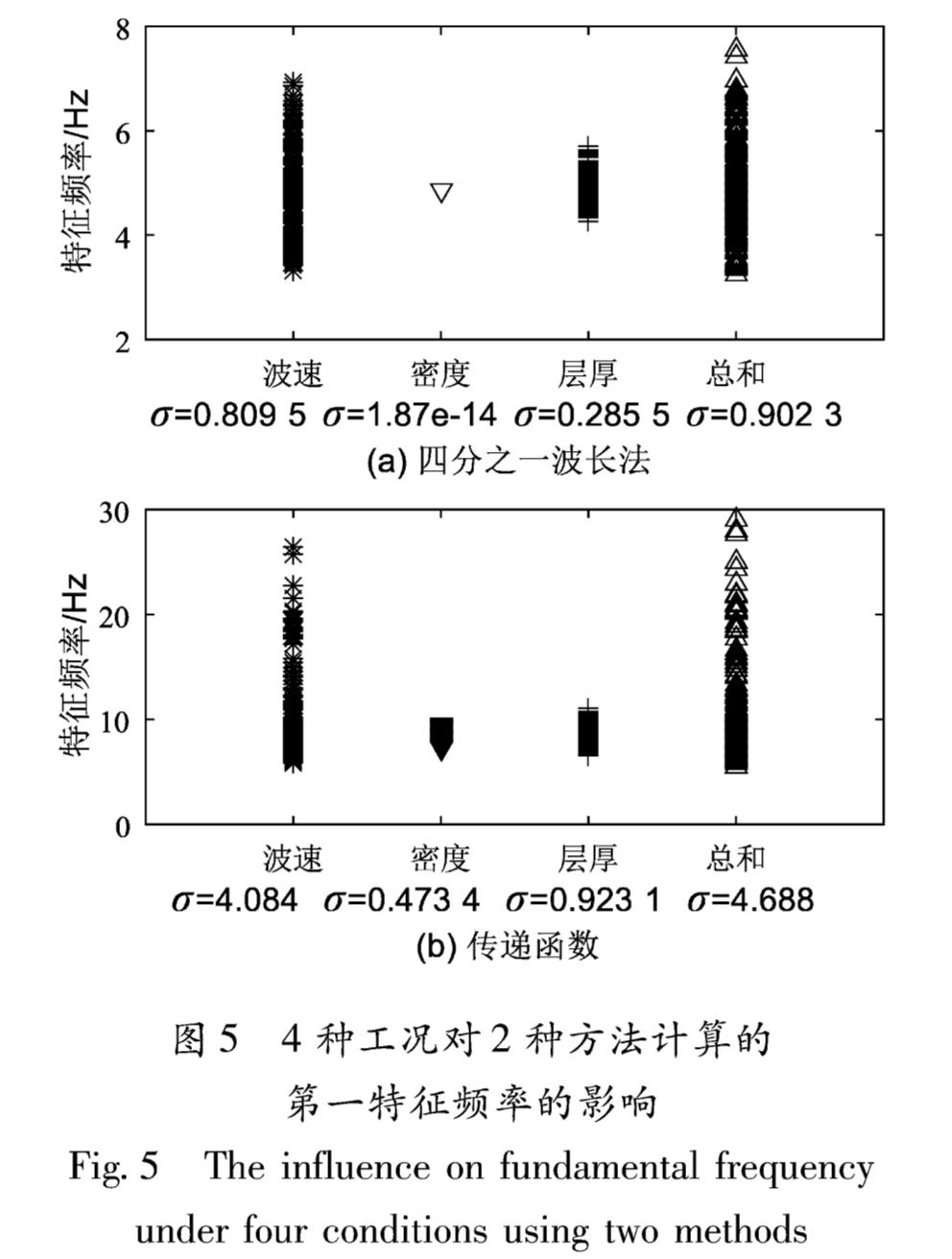
对比四分之一波长法第一拐点频率和传递函数法第一特征频率对各土层参数的敏感性,如图5所示。其中四分之一波长法的第一拐点频率是基岩面以上土层等效为单一均匀层的第一特征频率(对应场地卓越周期):
feq=(V^-(H))/(4H)(15)
式中:H为基岩面到地表的土层厚度; V^-(H)为厚度H的土层的平均剪切波速。而传递函数法计算的第一特征频率是精确值,反映了土层的固有特征。
由图5可知,四分之一波长法的第一特征频率对土层参数不确定的敏感度比传递函数法小约4~5倍,剪切波速的随机性对二者特征频率的影响最大,在四分之一波长法和传递函数法中分别约占总标准差的90%和80%。层厚的随机性对二者特征频率的影响几乎相同。密度的随机性对四分之一波长法的第一特征频率完全没影响,由式(15)可知四分之一波长法的第一特征频率没有考虑密度,而密度的随机性对传递函数的第一特征频率也只有较小的影响。
4 结论
本文采用Toro模型对Turkey Flat场地建立随机土层模型,对比4种工况对传递函数法和四分之一波长法放大因子的影响,并讨论2种方法放大因子和第一特征频率对各随机参数的敏感性,得到以下结论:
(1)相较于其他土层参数,剪切波速的随机性对2种方法计算的放大因子的影响最大,而且同时影响二者的幅值和特征频率。层厚的随机性对2种方法计算的放大因子的幅值影响小,对特征频率影响大。密度的随机性对2类方法计算的放大因子的幅值影响很小,几乎不影响二者的特征频率。
(2)2种方法的放大因子和特征频率对剪切波速的随机性最为敏感,其次是厚度的随机性。不同的是四分之一波长法对各随机参数的敏感度比传递函数法小4~5倍,四分之一波长法等效的特征频率对密度的随机性完全不敏感。
总体来说,虽然四分之一波长法能简化场地计算,但是土层剪切波速、层厚和密度的随机性对四分之一波长法的频谱特征影响和对传递函数的影响基本相同。而且由于四分之一波长对土层模型不确定性的敏感度弱于传递函数,所以用四分之一波长计算一类场地的放大因子时,产生的不确定性会小于传递函数法。
中国地震局工程力学研究所陶正如和陶夏新研究员给予了巨大支持和帮助,哈尔滨工业大学曹泽林博士和匿名审稿专家提供了宝贵的意见,在此一并表示感谢。
- 徐欢荣,袁晓铭.2014.浅硬场地剪切波速不确定性对场地地震反应的影响[J].地震工程与工程振动,34(4):123-129.
- 洪华生,邓汉忠,陈建兵,等.2017.工程中的概率概念——在土木与环境工程中的应用[M].北京:中国建筑工业出版社.
- 刘红帅,薄景山,吴兆营,等.2005.土体参数对地表加速度峰值和反应谱的影响[J].地震研究,28(2):167-171.
- Barani S,De Ferrari R,Ferretti G.2013.Influence of Soil Modeling Uncertainties on Site Response.[J].Earthquake Spectra,29(3):705-732.
- Bazzurro P,Cornell C A.2004.Ground motion amplification in nonlinear soil sites with uncertain properties.[J].Bull Seismol Soc Am,94(6):2090-2109.
- Boore D M,Joyner W B.1997.Site amplifications for generic rocksites[J].Bull Seismol Soc Am,87(2):327-341.
- Boore D M.2013.The uses and limitations of the square-root impedance method for computing site amplification[J].Bull Seismol Soc Am,103(4):2356-2368.
- Costantino C,Heymsfield E,Gu Y.1991.Site specific estimates of surface ground motions for the K-reactor site,Savannah River plant[R].N Y:Structural Analysis Div,Nuclear Energy Dept,Brookhaven National Laboratory.
- Day S M.1996.RMS Response of a One-Dimensional Half-space to SH[J].Bull Seismol Soc Am 86(2):363-370.
- Field E H,Jacob K H.1993.Monte Carlo simulation of the theoretical site response variability at Turkey Flat,California,given the uncertainty in the geotechnically derived input parameters[J].Earthquake Spectra,94(4):669-701.
- Joyner W B,Warrick R E,Fumal T E.1981.The effect of Quaternary alluvium on strong ground motion in the Coyote Lake,California,earthquake of 1979[J].Bull Seismol Soc Am,71(6):1333-1349.
- McGuire R,Toro G,O 'Hara T,et al.1989.Probabilistic seismic hazard evaluations at nuclear plant sites in the central and eastern United States:Resolution of the Charleston earthquake issue[R].Calif:Electric Power Research Institute.
- Rathje E M,Kottke A R,Trent W L.2010.Influence of input motion and site property variabilities on seismic site response analysis[J].J Geotech Geoenviron Eng,136(4):607-20.
- Real C R.1988.Turkey Flat,USA site effects test area:report 2,site characterization[R].Calif:Div of Mines and Geology Tech.
- Toro G R.1993.Probabilistic model of soil-profile variability,in Early Site Permit Demonstration Program:Guidelines for Determining Design Basis Ground Motions[R].Calif:Electric Power Research Institute.
- Toro G R.1995.Probabilistic models of site velocity profiles for generic and site-specific ground-motion amplification studies[R]N Y:Brookhaven National Laboratory.