由点震源发震引起的场地最大地震动参数A与震级M、震源距R有关(Esteva,1964):

A=b₁e^b₂MR^-b₃(1)

式中:b₁,b₂,b₃为拟合常数。

因此对于指定场地(即R=r),点震源发震引起的场地地震动参数A大于设防地震动参数A^～的概率P为:

P(A≥A^～〖JB<1|〗R=r)=P(b₁e^b₂MR^-b₃≥A^～〖JB>1|〗R=r)

=1-F_M[(ln(A^～/b₁r^-b₃))/(b₂)](2)

式中:F_M为震级累积分布函数。

Richter(1959)给出震级大于m的地震发生次数n_m与震级m的关系:

lnn_m=a-bm(3)

式中:a,b为待定系数。由此可得:

1-F_M(m)=e^-β(m-m₀)(4)

式中:m≥m₀,m₀是一个极小震级(对于建筑抗震设防可以忽略的震级); β=bln10。

将式(4)代入式(2),即为地震动参数A的超越概率分布函数:

1-F_A(A^～)=P(A≥A^～)=CG_PA^～^-β/b₂(5)

式中:C=exp[β(lnb₁)/b₂+m₀)],为与震级相关项; G_p=r^-βb₃/b₂,为场地位置项,p代表点震源; A^～为m₀对应的地震动参数,A^～=b₁e^b₂m₀r^-b₃为设防地震动参数下限。

以泊松计数过程作为地震发生概率模型已经广泛应用于地震工程学研究中。研究表明(高小旺,鲍霭斌,1985; 张超,翁大根,2013):沿地震带上地震的发生服从泊松分布,年平均发生率为v,在时间t内发生地震次数为N^～的概率为:

P_N^～(n)=P(N^～=n)=(e^-vt(vt)ⁿ)/(n!)(6)

在时间t内,地震动参数A超过设防地震动参数下限A^～的次数为N的概率为:

P_N(n)=P(N=n)=(e^{-P_A^～vt}(P_Avt)ⁿ)/(n!)(7)

式中:P_A=P(A≥A^～)=CG_PA^～^-β/b₂,为地震动参数A超过设防地震动参数下限A^～的概率; 在时间t内,地震动参数A^t_max小于设防地震动参数下限A^～的概率等同于在时间t内不发生大于设防等级的地震(N=0),即:

P_A(A^t_max≤A^～)=P(N=0)=e^{-P_A^～vt}(8)

将式(5)代入式(8)可得地震动参数A的累积分布函数:

F_A^(A)max=e^-P_Avt=exp(-vtCG_PA^-β/b₂)(9)

式中:A≥b₁e^b₂m₀r^-b₃。

假设点震源年发生震级大于4的地震概率为0.09,震源距为216 km。对于加速度,Esteva(1964)建议b₁,b₂,b₃取值分别为2000,0.8,2; 胡聿贤(2016)建议a,b分别取值5.87,0.696。代入式(5)可得C=2.4×10⁹,G_p=4.7×10^-10。将C,G_P,b₂,β=bln10=1.6带入式(9)可得场地的加速度超越概率函数和重现周期为:

1-F_A^(A)max=1-exp(-0.102tA^-2)(10)

T_A^(A)max=1/(1-exp(-0.102A^-2))≈9.85A²(11)

例如加速度2.25 gal的50年超越概率为63%,其重现周期为50年。当然场地周围潜在震源复杂,不可能只有一个。

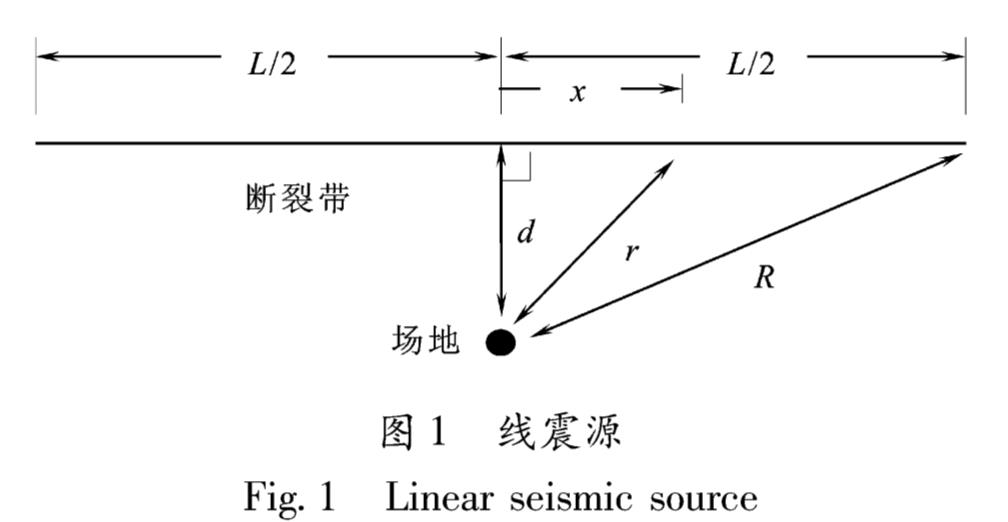
当建筑场地周围存在线性震源时,如图1所示,L为断裂带长度,d为断裂带中点发生点源地震时的震源距,R为场地至断裂带端点距离,r为场地至断裂带上任意点距离。线震源可以看作是长度为L的连续点震源,断裂带上每一点发生震动的概率均相等。因此由线震源发震引起的场地地震动参数概率分布等于点源地震概率分布沿断裂带全长的累积,即:

1-F_A(A^～)=P(A≥A^～)

=∫ ^R∫_d P(A≥A^～〖JB<1|〗R=r)f_R(r)dr(12)

式中:f_R(r)为震源距概率密度分布函数,可由震源距累积分布函数F_R(r)求得:

f_R(r)=((r²-d²)^1/2)/(L/2)(13)

式中:d≤r≤R。对r求导即为震源距概率密度分布函数:

f_R(r)=(dF_R(r))/(dr)=(2r)/(l(r²-d²)^1/2)(14)

式中:d≤r≤R。将式(14)代入式(12),则地震动参数A的超越概率分布为:

1-F_A(A^～)=P(A≥A^～)

=1/LCG_lA^～^-β/b₂(15)

G_l=(2π)/((2R)^γ)(Γ(γ))/([Γ((γ+1)/2)²])(16)

式中:G_l为场地位置项; l代表线震源; γ=βb₃/b₂-1; A≥b₁e^b₂m₀d^-b₃; C为震级相关项,见式(5)。

将式(15)代入式(8)可得地震动参数A的累积分布函数:

F_A^(A)max=e^-P_Av=exp(-v^{^}CGA^-β/b₂)(17)

式中:v^{^}=ν/L,为地震带每延米每年平均发震概率。

图1 线震源
Fig.1 Linear seismic source

当建筑场地周围存在圆环状面震源时,如图2所示,L为外环半径,l为内环半径,h为场地至环状中心深度,d为场地至内环任意距离,R为场地至外环任意点距离。面震源可以看作是点震源在环带面积内的均布,面震源内每一点发生震动的概率均相等。因此由面震源发震引起的场地地震动参数概率分布等于点源地震概率分布在圆环震源区域内的累积:

1-F_A(A^～)=P(A≥A^～)

=∫ ^R∫_d P(A≥A^～〖JB<1|〗R=r)f_R(2πr)dr

=1/(π(L²-l²))CG_aA^～^-β/b₂(18)

G_a=(2π)/((γ-1)d^γ-1)[1-(R/d)^1-γ](19)

式中:G_a为场地位置项,下标a代表面震源; γ=βb₃/b₂-1; A^～≥b₁e^b₂m₀d^-b₃; C为震级相关项,见式(5)。

将式(18)代入式(8)可得地震动参数A的累积分布函数:

F_A^(A)max=e^-P_Av=exp(-v^{^}CG_aA^-β/b₂)(20)

式中:v^{^}=ν/[π(L²-l²)],为面震源每平方米年平均发震概率。

图2 面震源
Fig.2 Planar seismic source

由于地壳构造复杂,建筑场地周围可能同时存在类型不同且数量不唯一震源。复合震源的地震动参数累计概率分布函数F_A^(A)max则为各震源发震引起的场地地震动参数的最大值均不大于设防地震动参数A,即:

F_A^(A)max=F_{A^(A)max_1}F_{A^(A)max_2}… F_{A^(A)max_n}=∏ⁿ_i=1F_{A^(A)max_i}(21)

式中:F_{A^(A)max_i}为第i个震源引起场地地震动参数最大值为A的累计概率分布函数。按照这种组合方式可以计算出类型、数量、深度随机组合的符合震源影响下场地地震动参数概率分布函数。上述震源相对于建筑场地均属于对称震源,对于非对称震源可以采用同种类型反对称震源进行组合并计算。

真实的建筑场地通常位于复合震源影响范围内,其场地地震动参数累计分布函数F_A^(A)max指数函数可以转化为:

F_A^(A)max=exp[-∑ⁿ_i=1v^{^}_iC_iG_iA^-β/b₂](22)

式中:地震动参数A的指数(-β/b₂)为负数,其中β,b₂反映地震动参数与震级和震源距,均为正数。可见,在复杂震源影响下,场地地震动参数累计分布函数式(20)属于极值Ⅱ型分布,极值Ⅱ型分布适用于具有下限、而无上限的分布,这与地震动参数实际情况相符合。现有研究表明地震烈度属于极值Ⅲ型分布,极值Ⅲ型分布适用于有上限的分布,这种分布符合地震烈度实际情况(人为规定烈度是有上限)。因此,直接根据场地地震动参数概率分布函数和设防水准计算设计地震动参数更为准确合理。

在第一节各类型震源对场地地震动参数分布影响分析中,假定了最大地震动参数A与震级M和震源距R的关系,即式(1),这一假定可以根据研究进展合理调整,例如温瑞智等(2017)分析芦山地震动使用的传播衰减关系,即:

ln(A)=a₀+a₁ln(R+a₂)+a₃ln(V_S30)+a₄R+ε(23)

式中:A为地震动参数; a₁,a₄为衰减项系数; a₂为拟合系数; a₃为场地放大系数; ε为残差; V_S30为30 m覆盖层平均剪切波速。假设a₁是震级M的直接关系项,将式(23)带入点震源式(5),可得:

1-F_I(A^～)=P[A≥A^～]=CGA^～^-β(24)

式中:ln(A^～)≥a₀(m₀)+a₁ln(R+a₂)+a₃ln(V_S30)+a₄R+ε, 震级关系项C=exp{β[a₃ln(V_S30)+ε+m₀]}, 场地位置项G=exp{β[a₁ln(R+a₂)+ a₄R]}。

式(24)中设防地震动参数A^～的指数为负数,因此其场地地震动参数累计分布函数仍属于极值Ⅱ型分布,对于其他传播衰减规律或复合震源同理可得相同结果。并且在第一节地震参数概率分布分析中所有参数均采用符号代替,没有采用具体数值,避免了数值化差异,式(22)中地震动参数A的指数为负数是定性结果,说明第一节的分析结果具有较好的工程通用性。