基金项目:国家自然科学基金项目(51608098,51508534)联合资助.
(1.北京工业大学 建筑工程学院,北京 100124; 2.中国地震局发展研究中心,北京 100036; 3.中国地震台网中心,北京 100045)
(1.College of Architectural and Civil Engineering,Beijing University of technology,Beijing 100124,China)(2.Development Research Center of China Earthquake Administration,Beijing 100036,China)(3.China earthquake Networks Center,Beijing 100045,China)
earthquake process; critical condition of instability; surface free energy; energy release rate
备注
基金项目:国家自然科学基金项目(51608098,51508534)联合资助.
基于能量平衡原理,把地震触发过程转换为数学、力学中系统发生局部失稳的问题,并理论推导给出了分析域内裂纹失稳临界条件; 基于线性断裂力学理论,给出了一些历史地震发震断层的表面自由能; 应用势能原理和GPS台网观测数据,提出了一个确定断裂能量释放率的计算方法; 进而给出了在断裂能量释放率与表面自由能基础上判定断裂发生地震可能性的一种方法。
Based on the principle of energy balance,the earthquake triggering process is transformed into the local instability problem of the system in mathematics and mechanics,and the critical condition of crack instability in the analysis domain is given by theoretical derivation.Based on the theory of linear fracture mechanics,the surface free energy of some historical earthquake-induced faults is given.Based on the principle of potential energy and the observation data of GPS network,a calculation method for determining the release rate of fracture energy is proposed.Furthermore,a method for determining the probability of earthquake occurrence of fracture based on the energy release rate of fracture and the surface free energy is developed.
引言
自古以来关于地震的起因就有多种说法,诸如地下雷、火山喷发、可燃性物质爆发燃烧、岩浆剧烈活动等。现在比较常见的地震成因学说有断层成因说、岩浆冲击成因说和相变成因说,其中断层成因说最为人所重视。
地下岩石受到长期的构造作用积累了应变能,当积累的能量超过一定限度时,地下岩层突然破裂,形成断层; 或者是沿已有的断层发生突然的滑动,释放出很大的能量,其中一部分以地震波的形式传播出去,形成地表震动,即弹性回跳理论(Reid,1910),这是Reid(1910)研究1906年旧金山大地震发震断层(圣安德烈斯断层)的地表破裂所得到的结论。
地震描述可以等效为边值条件下固体内部裂纹稳定性的力学问题(Rice,1976; Bigoni,2000),在远场边界持续加载过程中,或地幔物质移动作用下,一定温度下的岩石圈材料在裂纹处出现局部化变形。在分析域内,很多缺陷经历不可逆的生长,如空洞和已有裂纹的汇合、位错传播、新的缺陷成核; 同时不同类型的缺陷间会发生强烈的相互作用,促使位错、裂纹快速进化、扩展,导致域内材料逐步劣化; 裂纹周围有限区域内积累的应变能突然释放,促使裂纹失稳扩展,弹性回跳产生介质振动,以波的形式向四周传播,随后分析域进入调整期和新的积累期。
边界应力持续加载是长时间的过程,失稳是瞬时发生的。关于裂纹稳定性定义,可归结为:裂纹只有在外载荷不断增加时,才能持续扩展,如果外载荷保持不变,裂纹就不继续扩展,则可以认为裂纹状态是稳定的; 反之,若在外荷载不变情况下,裂纹持续加速扩展,则该裂纹状态为不稳定(阿特金森,1992)。
设分析域中存在势函数Π,在某一平衡状态下有一任意小的扰动,此势函数获得一增量△Π,用Taylor级数在此平衡位置处展开:
ΔΠ=δΠ+1/(2!)δ2Π+…(1)
式中:δΠ=0是平衡状态保持稳定的充分条件。当ΔΠ>0和δ2Π>0时,系统是稳定的; 当δ2Π<0时系统是不稳定的; 当δ2Π=0时,系统处于一个临界点,系统有可能稳定,也有可能不稳定。
按照脆性失稳定义,地震发生是没有前兆的,但由于人类知识的非完备性和地震发生的复杂性,应用GPS观测裂纹的物理场,联合断裂力学方法,可以有效评估滑动断层近期地震的危险性。本文从能量平衡原理出发,把地震触发过程转换为数学、力学中系统发生局部失稳问题,给出分析域内局部失稳临界条件。计算了部分地震发震断层的表面自由能,并给出了计算裂纹能量释放率方法。
1 地震发生的临界条件
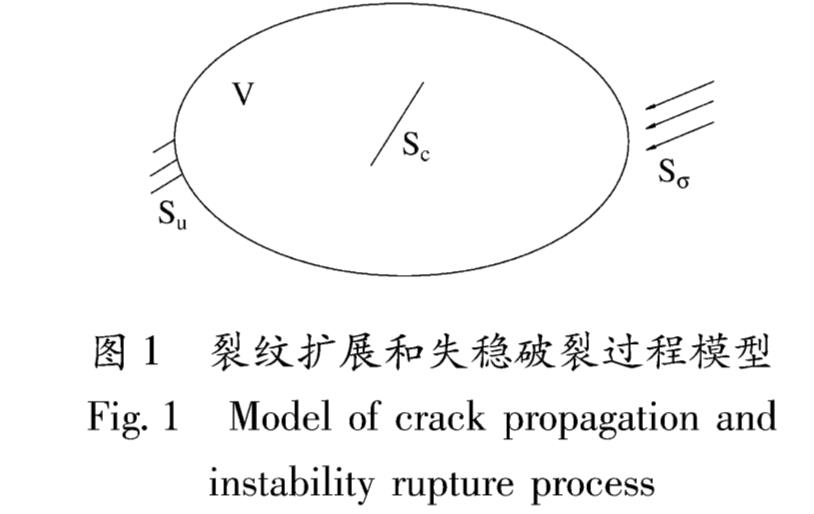
假设包含一条裂纹的固体分析域为V,体力为b; 应力边界为Sσ; 应力φ; 位移边界为Su; 位移为u^-; 裂纹边界为Sc,则应力为φc,平衡方程为:
σ+b={0 Earthquake
ρü ∈Earthquake (2)
固体本构关系形式为:
σ=Dε或σ·=Dε·(3)
式中:D为介质的弹性刚度张量。
在拟静力加载条件下,建立满足式(2)和(3)初边值条件的介质出现裂纹扩展和裂纹失稳破裂过程模型(图1),其中包括拟静力应变能积累过程和系统失稳的地震过程。
由于裂纹存在,固体内部位移场为u=u+[[u]]HS,HS为裂纹处的阶跃函数,裂纹处作用力为φc,相应的势能原(Washizu,1982)为:
Π=∫V\SWdV-∫VbVdV-∫SσφudS-∫Sunσ(u-u^-)dS-∫Scφc[[u]]dS(4)
式中:W为应变能密度,W=∫0εσdε。
δΠ=0,即有:
-∫V\Sδu(σ+b)+∫Sσδu(nσ-φ)-
∫Suδ(nσ)(u-u^-)+∫Scδ[[u]](nσ-φc)=0(5)
式(5)左边前3项分别对应平衡方程、应力边界条件和位移边界条件。笔者关注的是第四项,只有符合裂纹扩展条件,即:φc=n[σc(Gc)],才存在裂纹稳态扩展,即:
σ(G)-σc(Gc)=0(6)
式中:G是裂纹扩展的能量释放率; σ(G)是以G表述的应力; Gc是裂纹表面自由能,其值为2Γ; σc(Gc)是以Gc表述的材料破坏应力。
式(6)也可以采用应力强度因子K和J积分来表述,三者存在确定的关系,且在拟静态过程中等效。需要说明,在经典断裂力学中,裂纹尖端的应力具有奇异性,式(6)中的σ(G)改为G(σ)可能更好理解; 但在分子动力学分析中,材料破裂的本质是原子键的断裂。
由式(1)知,临界稳定性条件为:
δ2Π=-∫V\Sδu(δσ)dV+∫Sc{n·δ[σ(G)-σc(Gc)]·δ[[u]]}dS=0(7)
对于岩石圈材料,σc(Gc)在裂纹扩展过程中有所变化,在均匀脆性材料中,仅当δσc(Gc)=0时,才能与线性断裂力学一致; 一般地,当分析域内存在一裂纹时,不管是基于线性还是非线性断裂力学观点,裂纹尖端存在应力集中区,裂纹附近区域积累的应变能消耗就会集中在裂纹扩展上。
域内刚度(式(7)第一项)会从加载阶段进化为弹性卸载分叉状态,即式(7)右边第一项为0。因此裂纹失稳扩展的临界条件为:
∫Sc{n·δ[σ(G)-σc(Gc)]·δ[[u]]}dS=0(8)
把裂纹剖分为有限个子段Sci,上式转化为:
∑i∫Sci{nδ[σ(G)-σc(Gc)]·δ[[u]]}dS=0(9)
当子段足够小,且能识别裂纹尖端时,式(8)等价于:
nδ[σ(G)-σc(Gc)]·δ[[u]]=0(10)
由式(6)可知:
δσ=(∂σ)/(∂G)(∂G)/(∂Sc)δSc,δσc=(∂σc)/(∂Gc)(∂Gc)/(∂Sc)δSc(11)
已知σ和G具有确定关系,且(∂σ)/(∂G)=(∂σc)/(∂Gc),其值设为ξ。把式(11)代入式(10),有:
n·((∂G)/(∂Sc)-(∂Gc)/(∂Sc))δSc·δ[[u]]=0(12)
按照断裂力学之能量释放率的定义,无论裂纹扩展沿自身平面还是转向,其尖端扩展均采用了移动坐标规定,即δSc与δ[[u]]反向(李世愚等,2010)。考虑特殊向量δ[[u]]=-g和δSc=hn,其中,h≠0,g≠0,n∈〖JB<1|〗n〖JB>1|〗=1,合并g·h=D,则式(12)变化为:
n·((∂Gc)/(∂Sc)-(∂G)/(∂Sc))·n·D=0(13)
上式为D的齐次线性方程,非0解条件为:det[n·((∂Gc)/(∂Sc)-(∂G)/(∂Sc))·n]=0,此为裂纹非形状改变的失稳扩展临界条件。
特殊情况下,当仅考虑3种基本断裂情况时,失稳扩展临界条件为:
(∂GJc)/(∂Sc)-(∂GJ)/(∂Sc)=0, J=Ⅰ,Ⅱ,Ⅲ(14)
失稳扩展条件为:
(∂GJc)/(∂Sc)-(∂GJ)/(∂Sc)<0, J=Ⅰ,Ⅱ,Ⅲ(15)
由此不难得出,若分析域内能量释放率G与表面自由能Gc线性变化时,失稳扩展条件为Gc<G。在满足式(15)时,结合式(2)可判断由新生破裂或断层胶结后的再次破裂的地震发生。
2 能量释放率与裂纹表面自由能
2.1 能量释放率G能量释放率G定义为limSc→0(-(δΠ)/(δSc)),即在裂端区释放出的能量,驱动裂纹的扩展。其值可采用标准断口试件进行恒定外力或位移试验直接测定,但常用的方法则是应用G和K的关系进行转换,对于3类基本断裂形式有:
Gi=K2i/E'i, i=1,2,3
E'1=E'2=E^-(16)
E'3=E^-/(1+υ^-)
式中:E^-,υ^-分别为含小裂纹材料的等效弹性模量和泊松比。
应力强度因子K仅与外加荷载形式、扩展路径和岩体裂纹几何形状有关,具体见《应力强度因子手册》(中国航空研究院,1981)。但对岩石介质来讲,其中的裂纹不仅尖端存在应力,在裂纹面也存在着由摩擦律确定的应力,再加上岩层变化与缺失、岩体的微观结构与组构、构造环境与自然环境等因素的影响,得到一段断裂可靠的应力强度因子K也是不易的。
2.2 裂纹表面自由能Gc表面自由能Gc定义为2Γ,Γ是形成单位裂纹所需的能量。一般应用Gc和Kc的关系进行转换,对于3类基本断裂形式有:
Gci=K2ci/E'i, i=1,2,3
E'1=E'2=E^-(17)
E'3=E^-/(1+υ^-)
到目前为止,岩石断裂韧性Kc试验已使用了许多不同的试件类型及方法,其结果相差很大,意味着测出的结果通常不能真正代表材料的性质。因此,国际岩石力学学会(ISRM)测试方法委员会推荐了试验方法,尽管方法也有上述问题,但仔细的试件制作、加载条件和测量精度要求,对定量的比较应用还是具有重要意义的。
3 发震断裂的表面自由能和能量释放率估算
3.1 发震断裂的表面自由能估算现今岩石圈内的材料是不同时期的产物,不同地质构造期内主营造力不同,环境温度、湿度、压力不同,材料的结晶、解理等物理和化学过程存在差异,致使材料的结构和组构不同,造就了不同规模断裂、裂隙、裂纹分割岩石圈内的不同级别的块体。
不同规模断裂形成是由热过程或力学过程引起的,其扩展特性与系统内存储的能量、岩体和裂纹特性相关。抵抗裂纹扩展的表面自由能不仅与裂纹尖端的微观结构和组构特性直接相关,还与温度、流体、应力腐蚀相关。在有压流体作用下,活性物质的迁移会导致裂纹尖端的微观结构变化; 表面自由能除涉及到的机械能部分外,还有特定环境下裂纹尖端的塑性功、热能、化学反应能量等。
因此,得到较可靠的Gc是困难的; 但是应用已发生的地震参数和弹性断裂力学可估算Gc。假定一次地震的地表破裂有效长度为L,应力降为Δσ,则破裂上位移分布为:
d(x)=(2Δσ)/(μ(1+υ))(L2-x2)1/2(18)
式中:μ和υ分别为岩石介质的剪切模量和泊松比,这里分别取35 GPa和0.25(阿特金森,1992)。
假定地震为中间破裂向两侧扩展,最大位移dmax在断裂的中心,表面自由能为(阿特金森,1992):
Gc=(π)/8μ(1+υ)(d2max)/(L)(19)
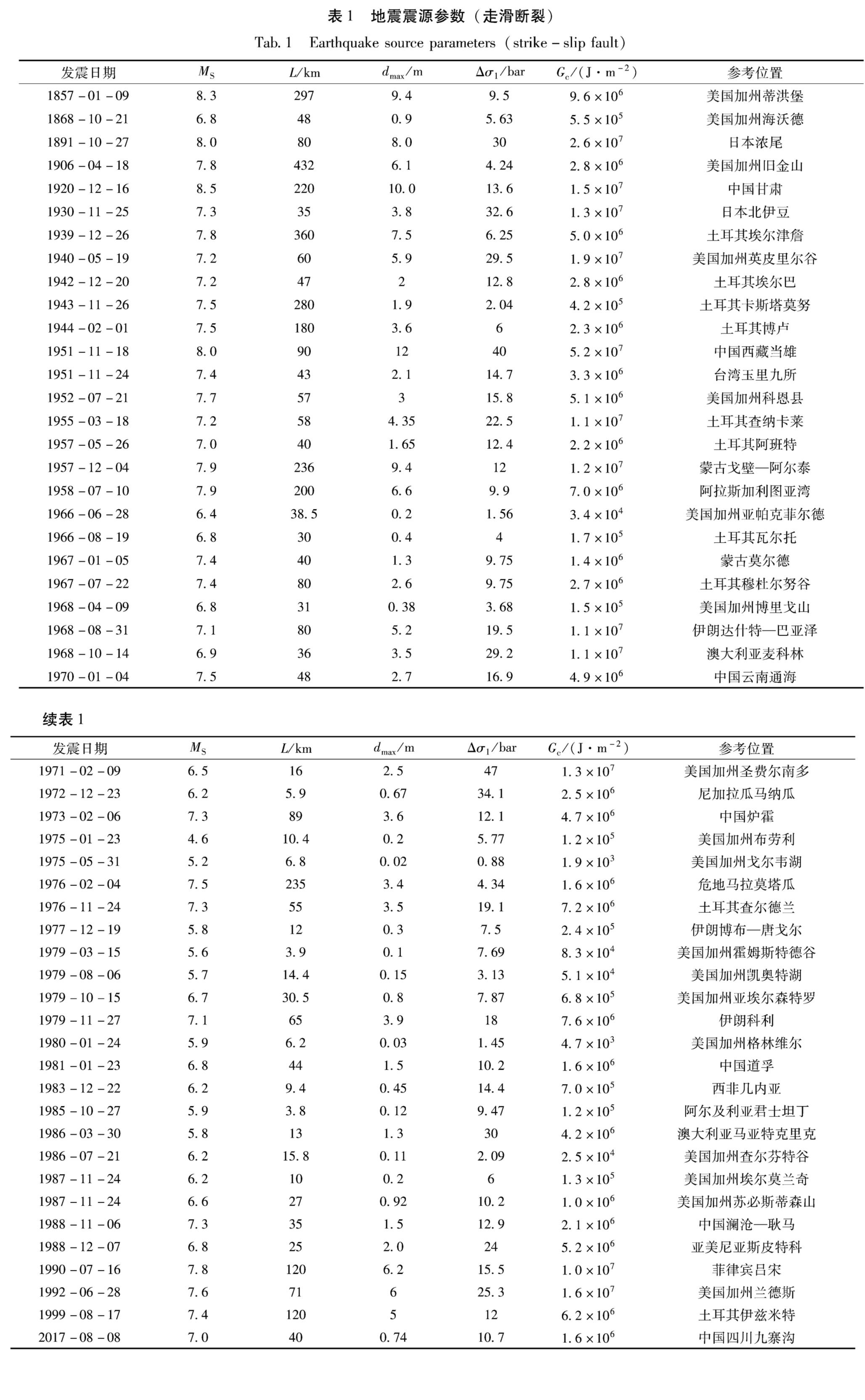
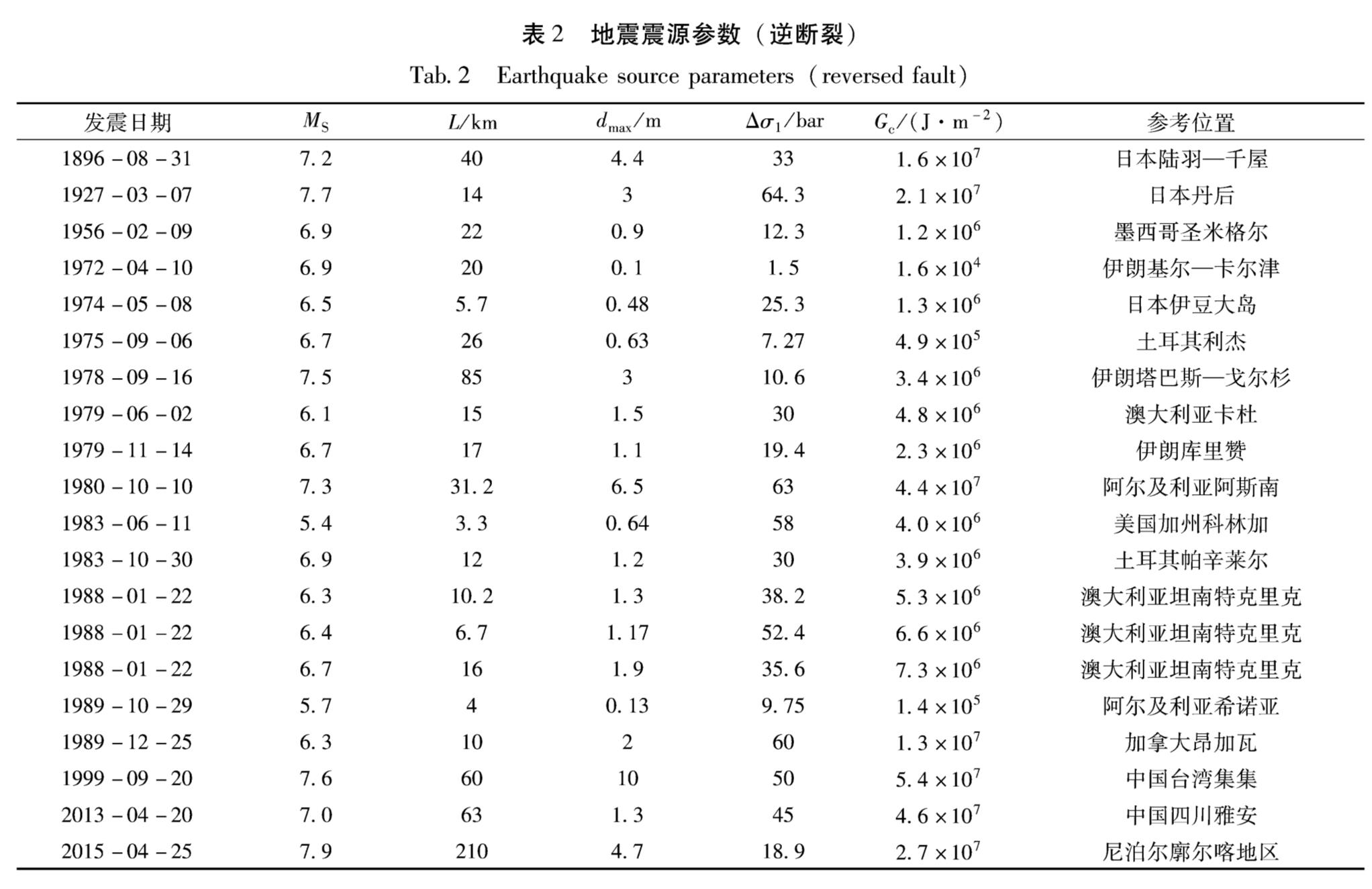
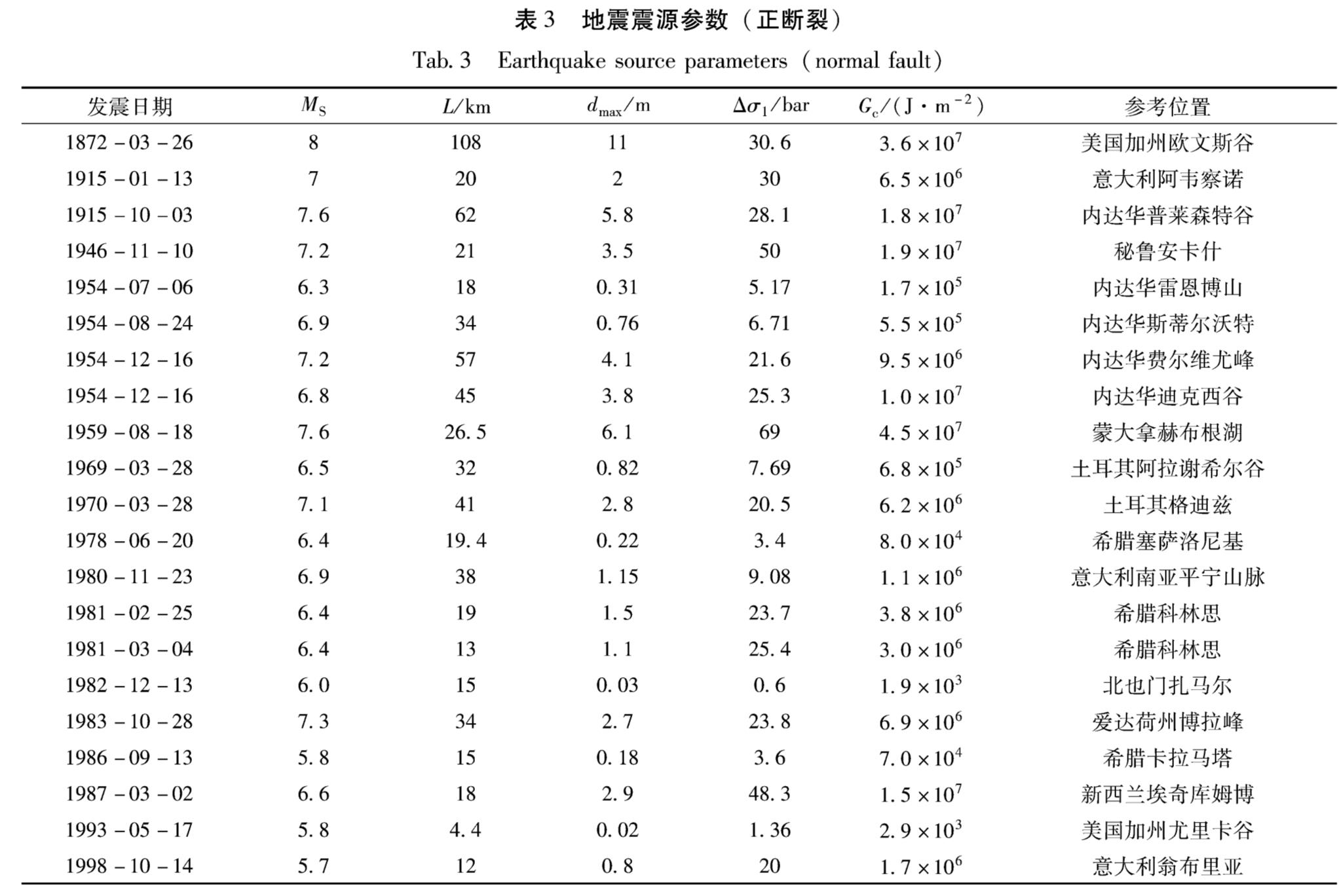
采用Mohammadioun和Serva(2001)研究中的地震资料和近年来发生的典型破坏地震资料(张勇等,2013; Shen et al,2017; 申文豪等,2019),计算了走滑、逆和正断裂的Gc,见表1~3。如果考虑地震破裂发生在地壳浅层,比如岩石圈厚度为50 km的10 km处,那么表中Gc加权因子为5左右(阿特金森,1992)。由表1可知,走滑断裂引起的地震表面自由能最大为5.2×107 J/m2。由表2可知,逆断裂引起的地震表面自由能最大为5.4×107 J/m2。由表3可知,正断裂引起的地震表面自由能最大为4.5×107 J/m2。
3.2 发震断裂的能量释放率估算地质体内裂纹尺度跨越微米到千千米之间,求解发震断层(段)的G值,目标是分析域内裂纹尺度最显著的几条。当裂纹尺度与分析域尺度之比很小时,即:相应块体分析域内存在一条或多条较短的断裂时,可以采用域内损伤来处理,得到等效的弹性参数(宁建国等,2012)。
在分析域内,以有限个跨越断裂的GPS值和局部构造应力场方向,对K进行求解。具体的变分原理为:
Π*=Π+α∑nGPSk=1(uk-uk^-)2(20)
式中:α是罚函数,Π见式(4),域边界处的测点GPS观测值作为位移边界。
远离裂纹的位移采用有限单元标准离散,裂纹尖端采用半解析形函数,得到计算域内整体有限元格式,求解以上方程得到位移场、应变场和K(董玉文,2008),通过式(16)得到断裂现阶段的G值。
应用式(6),理论上可以评估断裂近期发生地震的危险性。以口泉断裂北段为例,该断裂北段长30 km,倾向SE,倾角65°~85°,右旋正走滑断裂,由山西盆地南北两端4个地区共计13个深钻孔中水压致裂地应力测量获得,盆地北端五台山、雁门关地区深度400~600 m,最大水平主应力值为8~12 MPa(陈群策等,2010)。根据《应力强度因子手册》(中国航空研究院,1981)求得应力强度因子k1=δ(πl)1/2(其中δ为主应力; l为裂纹长度的二分之一),弹性模量E=2(1+υ)μ(其中υ为泊松比; μ为剪切模量),结合式(16)求得G值为(3.5~7.8)×107 J/m2,对照表1和表3中对应的Gc,依据式(15)推断口泉断裂北段应处于危险状态。
按照脆性失稳定义,地震发生是没有前兆的,但实际上地震的孕育和发生是一个复杂的过程,加之对于地壳介质的多相性、断裂深部几何构造与物理特征、区域构造运动的非均匀性等的认知的非完整性,故不能排除一些地震存在的征兆。
此处不讨论地震将要发生的前兆,而是限定在区域内几条活动断裂,进行长时间(最好10年以上)的跨断层GPS观测(张国安等,2002; 王瑞平,潘振生,2009; 吴云等,2003)以及应变和应力实地测量(陈启林等,2002; 胡卫建等,2002; 谢富仁等,2005),量化沿断层位移场、应变场和应力场的变化,确定闭锁范围的尺度,估算未来发生地震的震级; 在进行长时间沿断层的考察时,尤其要注意裂纹(或闭锁范围)尖端的位移变化,比如出现鼓包、凹陷和剪切裂纹等局部现象,当局部变形变化剧烈时,理论分析能量释放率和断裂表面自由能之间的关系,评估地震发生的可能性。
4 结论与讨论
本文针对单一裂纹连续介质内地震发生的临界条件、能量释放率与裂纹表面自由能进行了理论分析,得到的主要结论如下:
(1)从能量原理出发,可把地震触发过程视为数学、力学中系统发生局部失稳问题,并推导出分析域内局部失稳临界条件为新生破裂或断层胶结后的再次破裂,即地震发生条件。
(2)基于线性断裂力学理论,统计分析了震源参数较全的一些历史地震发震断层的表面自由能,结果表明,走滑断裂、逆断裂、正断裂引起的地震表面自由能最大分别为5.2×107 J/m2,5.4×107 J/m2,4.5×107 J/m2。
(3)依据应用势能原理,提出了一个由GPS台网观测数据确定断裂能量释放率的计算公式,为进行特定断裂近期发生地震的可能性的判定提供了方法。
按照脆性失稳定义,地震发生是没有前兆的。然而由于对地壳介质、断裂深部几何构造、区域构造运动认知的非完整性,不能排除一些地震会存在前兆。通常地震发生前,发震断裂区域范围内的位移场会产生变化,尤其在断裂端部产生诸如鼓包、凹陷和裂纹等局部位移异常,当这些异常显著时,可由理论分析能量释放率和断裂表面自由能之间的关系,判断地震发生的可能性。GPS是位移场观测的一个重要工具,它不仅能给出断层附近的位移场分布,还可以分析闭锁区域的范围和能量积累,这为本文方法的应用提供了数据基础。
本文计算应力、裂纹能量释放率等的方法基于实验室中得到的材料和岩石力学原理公式,而实际中的地表断层的大规模运动、物质迁移和地震现象与实验室中的实验有着显著的不同。目前的实验还无法完全真实地模拟出真实地震的应力积累和发生机制,这也是当前地震研究的难点之一。本文理论计算与实际的差异除了来自于数据来源的可靠性、模型的不确定性等因素之外,实验中的岩石材料与实际地壳断层的本质区别也是重要的因素。因此,本文提出的判定断层危险状态的方法可以作为一种思路的尝试,但要形成完整理论体系、真正在实际地震中得到应用,还需要对模型、公式做大量的改进。
- 阿特金森.1992.岩石断裂力学[M].北京:地震出版社.
- 陈启林,王皓,毛华锋,等.2002.体应变数字记录特征与中强震关系初探[J].华南地震,22(1):76-79.
- 陈群策,安其美,孙东生,等.2010.山西盆地现今地应力状态与地震危险性分析[J].地球学报,31(4):541-548.
- 董玉文,余天堂,任青文.2008.直接计算应力强度因子的扩展有限元法[J].计算力学学报,25(1):72-77.
- 胡卫建,张俊山,谢智,等.2002.荷载对钻孔应变测值影响的实验及力学解析[J].地震,22(3):95-104.
- 李世愚,和泰名,尹祥础.2010.岩石断裂力学导论[M].合肥:中国科学技术大学出版社.
- 宁建国,任会兰,方敏杰.2012.基于椭圆形微裂纹演化与汇合的准脆性材料本构模型[J].科学通报,57(21):1978-1986.
- 申文豪,李永生,焦其松,等.2019.联合强震记录和InSAR/GPS结果的四川九寨沟7.0级地震震源滑动分布反演及其地震学应用[J].地球物理学报,62(1):115-129.
- 王瑞平,潘振生.2009.阿克苏跨断层形变观测资料分析及其与地震关系的研究[J].内陆地震,23(1):51-55.
- 吴云,孙建中,乔学军,等.2003.GPS揭示的现今地壳运动与地震前兆特征[J].大地测量与地球动力学,23(3):13-20.
- 谢富仁,邱泽华,王勇,等.2005.我国地应力观测与地震预报[J].国际地震动态,(5):54-59.
- 张国安,陈德福,陈耿琦,等.2002.中国地壳形变连续观测的发展与展望[J].地震研究,25(4):383-390.
- 张勇,许力生,陈运泰.2013.芦山4·20地震破裂过程及其致灾特征初步分析[J].地球物理学报,56(4):1408-1411.
- 中国航空研究院.1981.应力强度因子手册[M].北京:科学出版社.
- Bigoni D.2000.Bifurcation and Instability of Non-associative elastoplastic solids[C]//CISM Courses and Lectures of Material Instabilities and Plastic Solid.H Petryk(ed)New York:Springer-Verlag,1-52.
- Mohammadioun B,Serva L.2001.Stress Drop,Slip Type,Earthquake Magnitude,and Seismic Hazard[J],Bulletin of the Seismological Society of America,91(4):694-707.
- Reid H F.1910.The Mechanics of the Earthquake,The California Earthquake of April 18,1906[R].Washington D C:State Earthquake Investigation Commission:43-47.
- Rice J R.1976.The localization of plastic deformation[M].North Holland Amsterdam:Theoretical and Applied Mechanics,207-220.
- Shen W H,Li Y S,Zhang J F.2017.Hybrid stochastic ground motion modeling of the MW7.8 Gorkha,Nepal earthquake of 2015 based on InSAR inversion[J].Journal of Asian Earth Science,141(B):268-278.
- Washizu K.1982.Variational methods in elasticity and plasticity[M].England:Cambridge University Press,3rd edition.