许多学者利用不同模型对强震的平均发生率进行了有益的研究和探索,研究主要集中在强震的累积地震次数随时间变化模型的探讨上,张国民和傅征祥(1985)通过对华北强震时间分布特征研究,认为大地震的累积频度曲线随时间的变化呈指数函数形式; 秦嘉政等(2009)对云南强震活动时间间隔研究认为,地震的累积频次随发震时间呈幂函数变化; 傅征祥等(1998)和刘杰等(1998)利用一个假想的泊松分布时间序列,分别采用双指数和指数模型对强震发生率进行了研究,本文将采用相同的时间序列系统地对事件累积次数随时间的变化规律进行研究。

假设地震事件序列相邻地震间隔时间为:1,3,4,5,10,30,40,50。考虑3种典型排列方式:时间间隔递减、时间间隔递增和时间间隔不规则,分别表示地震活动的加速、减速和线性变化。采用Matlab语言非线性回归模型方法进行参数估计(陈桂明等,2002),对3种排列方式下幂函数、指数函数和双指数函数模型进行非线性拟合参数计算,结果表明幂函数方法直接拟合效果最佳。图1作为例子给出幂函数模型非线性拟合曲线,可以看到,累积曲线的变化趋势与实际累积频次符合程度较好。

假设地震事件为泊松过程,地震累积频度N(t)是一种呈幂指数的增长过程:

N(t)=at^b+c(6)

式中:a,b和c是常数,根据非线性回归模型方法可对参数进行估计。

对于稳态泊松过程,地震事件的平均发生率v_c

(a)时间间隔Δt递减

(b)时间间隔Δt递增

(c)时间间隔Δt不规则

图1 累积频次与发生时间幂函数模型非线性拟合曲线
Fig.1 Nonlinear fitting curve of power function model of cumulative frequency with occurrence time

为常数,由式(5)计算得到v_c=0.06次/年。而对于非稳态泊松过程,地震事件的瞬时发生率v(t)为:

v(t)=(dN(t))/(dt)(7)

式中:v(t)为包含a,b 2个参数的t时刻的瞬时发生率。图2作为例子给出假想地震事件时间间隔逐渐减小情况下累积频度和发生率。由图2a可见,对于稳态泊松过程,累积频度N随时间t呈线性增长,发生率v_c为直线的斜率。对于非稳态泊松过程,累积频度N随时间t呈非线性增长,随着时间的增长单位时间发生的地震越多。图2b显示,对于稳态泊松过程,发生率v_c为水平直线,在整个过程中恒定不变。对于非稳态泊松过程,根据式(7)计算的各个时刻的瞬时发生率v(t)呈非线性变化。

图2 地震事件时间间隔逐渐减小情况下累积频次(a)和地震发生率(b)
Fig.2 Cumulative frequency and earthquake occurrence rate with decreasing time interval of earthquake events

对于稳态泊松过程,根据式(4)和(5)可得(未来)时间t内至少发生一次地震的概率为:

P=1-exp(-v_ct)=1-exp(-N/Tt)(8)

式中:T为研究时间段的长度; N为在T内的地震总数。

对于非稳态泊松过程,根据式(2)和(7),假定t₀时刻发生一次地震,则在[t₀,t₀+t]时段内至少发生一次地震的概率为:

P=1-exp[-∫_t0^t₀+tv(τ)dτ](9)

图3给出假想地震序列时间间隔逐渐减小情况下累积频度拟合预测及概率,在图3a中,空心圆表示根据非线性拟合曲线给出的当最后一次地震后t=10 a时刻的预测值。在图3b中,水平虚线表示不论事件发生在什么时间,其后t=10 a的事件发生的概率都是相同的,为P=0.43。在非稳态泊松过程中,地震发生呈非线性加速增加,间隔时间越来越短,越到后面越容易发生地震,如图3b所示,在最初的时间间隔Δt较长的3个点发震概率P较低,低于水平直线稳态泊松过程,从第四个点开始发震概率P激剧增加。

稳态泊松过程模型表示的是地震序列整体的平均状态,不考虑序列地震的活跃、平静过程,得到的发震概率P在整个研究时间段内都是相同的。而在非稳态泊松过程模型中,随着地震的活跃、平静状态不同,模型得到的发震概率P也不相同,更能真实地反映不同时间段发生地震的危险程度。

图3 地震事件时间间隔逐渐减小情况下累积频次(a)和概率(b)
Fig.3 Cumulative frequency and probability with decreasing time interval of earthquake events

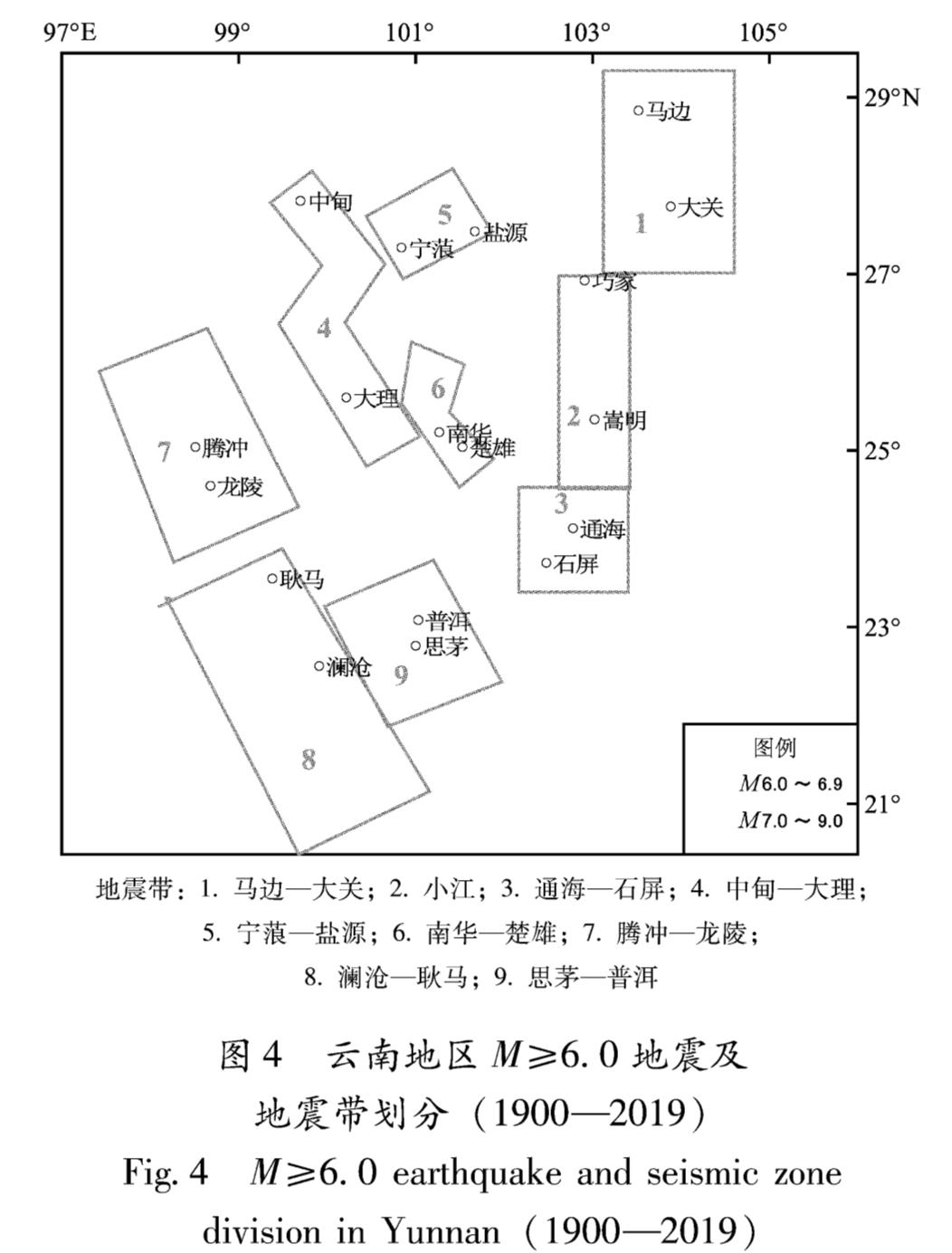
云南地区(20.5°～29.3°N,97.2°～106°E)M≥6.0地震在空间分布上极不均匀,主要沿活动断裂展布,尤其是沿有较强活动水平的深大断裂分布。根据云南地区M≥6.0地震的地震活动重复性、地震类型特征与地质构造关系,皇甫岗等(2010)将M≥6.0地震划分为9个主要地震带(区),如图4所示。1900—2019年,云南地区共发生M≥6.0地震95次,9个地震带内有地震78次,占82%。若按云南省界统计,云南省内共有地震61次,仅有4次地震位于地震带外,即云南省内93%的M≥6.0地震均处于这9个地震带内。

取各个地震带M≥6.0地震,若地震带内地震活动相对较弱,可适当降低起始震级,如宁蒗—盐源地震带。根据式(6),对各地震带地震序列进行非线性拟合,从拟合方程可以计算下一次地震应该发生时间t,如果t小于目前时间,表明理论计算的地震在过去就应该发生,但实际上却未发生,表明地震发生的危险性较大。反之,如果计算得到的t值大于目前时间,表明理论计算的地震应该在将来发生,意味着地震发生的危险性相对较小。因此,通过计算一次地震的发震时间可以对地震危险性进行初步判断。

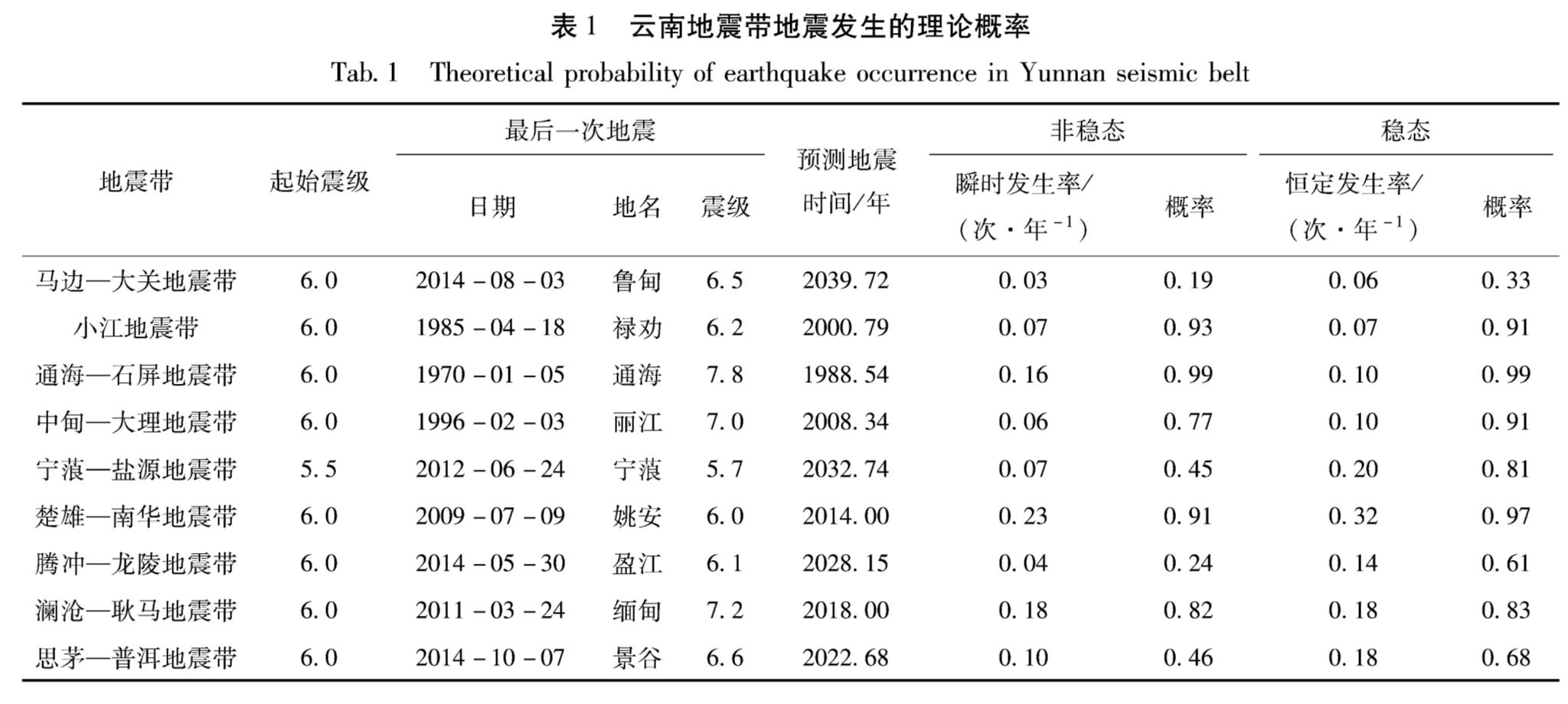
表1给出云南9个地震带参数及危险性概率结果,图5给出云南各地震带历史地震M-t图和累计频度N-t图及其非线性拟合曲线。假设截止时间一律为2019年12月31日,在图5的M-t图中用红色虚竖线表示,在N-t图中,分别给出了稳态和非稳态计算结果,红色空心圆表示按非线性拟合得到的方程计算的下一次地震应该发生的时

地震带:1.马边—大关; 2.小江; 3.通海—石屏; 4.中甸—大理;

5.宁蒗—盐源; 6.南华—楚雄; 7.腾冲—龙陵;

8.澜沧—耿马; 9.思茅—普洱

图4 云南地区M≥6.0地震及地震带划分(1900—2019)
Fig.4 M≥6.0 earthquake and seismic zone division in Yunnan(1900—2019)

间,表1给出了具体计算参数。

马边—大关地震带发生M≥6.0地震7次,最后一次地震是2014年8月3日鲁甸M6.5地震,预测的下一次地震应该发生在2039年,目前时间远远未到理论应发震时间,初步判断该地震带目前发生地震的危险性较小。

小江地震带发生M≥6.0地震5次,最后一次地震是1985年4月18日禄劝M6.2地震,预测的下一次地震应该发生在2000年,目前时间远远超过理论应发震时间,初步判断该地震带目前发生地震的危险性较大。

通海—石屏地震带发生M≥6.0地震7次,最后一次地震是1970年1月5日通海M7.8地震,预测的下一次地震应该发生在1988年,目前时间远远超过理论应发震时间,初步判断该地震带目前发生地震的危险性较大。

中甸—大理地震带发生M≥6.0地震9次,最后一次地震是1996年2月3日丽江M7.0地震,预测的下一次地震应该发生在2008年,目前时间超过理论应发震时间,初步判断该地震带目前发生地震的危险性较大。

宁蒗—盐源地震带发生M≥5.5地震8次,其中6.0～6.9级地震3次,由于该地震带6级以上地震较少,因此将该地震带起始震级适当下降为5.5级,该地震带最后一次地震是2012年6月24日宁蒗M5.7地震,预测的下一次地震应该发生在2032年,目前时间远远未到理论应发震时间,初步判断该地震带目前发生地震的危险性较小。

楚雄—南华地震带发生M≥6.0地震5次,最后一次地震是2009年7月9日姚安M6.0地震,预测的下一次地震应该发生在2014年,目前时间超过理论应发震时间,初步判断该地震带目前发生地震的危险性较大。

腾冲—龙陵地震带发生M≥6.0地震14次,最后一次地震是2014年5月30日盈江M6.1地震,预测的下一次地震应该发生在2028年,目前时间未到理论应发震时间,初步判断该地震带目前发生地震的危险性较小。

澜沧—耿马地震带发生M≥6.0地震17次,其中7级以上地震多达8次,是云南地区7级以上大地震最容易发生的地震带,该地震带最后一次地震是2011年3月24日中缅交界M7.2地震,预测的下一次地震应该发生在2018年,目前时间略超过理论应发震时间,初步判断该地震带目前存在发生地震的危险性。

思茅—普洱地震带发生M≥6.0地震11次,无7级以上地震,该地震带是云南地区6级地震最集中的地震带,最后一次地震是2014年10月7日景谷M6.6地震,预测下一次地震应该发生在2022年,目前时间未达到理论应发震时间,初步判断该地震带目前发生地震的危险性小。

从以上分析可以得知,假定未来地震的发展趋势遵循历史演化规律,则可以用计算的下一次地震发生时间的方法对未来地震进行定性判定,但无法进行定量描述,只能对地震危险性进行初步判断。从表1还可以看到,计算的下一次地震发生时间的误差还是较大的,误差最大达26年,大多数误差在8年以内,误差偏大的主要原因是样本的时间跨度长而样本数又不多。如果简单按照计算得到的下次地震理论计算时间从小到大排序,可初步将云南地震带地震危险性的危险程度从高到低排列如下:通海—石屏地震带、小江地震带、中甸—大理地震带、楚雄—南华地震带、澜沧—耿马地震带、宁蒗—盐源地震带、思茅—普洱地震带、马边—大关地震带。

图5 云南地区地震带M-t图和N-t图
Fig.5 M-t and N-t diagrams of the seismic zone in Yunnan

利用基于非稳态泊松分布的概率模型来对地震带地震危险性进行定量判定。假定t₀时刻发生一次地震,则在[t₀,t₀+t]时段内至少发生一次地震的概率可以用式(9)计算,在本文的研究中,统一取2019年12月31日为截止时间,以式(9)计算2019年12月31日以后t_p=1年各地震带至少发生1次地震的概率,t_p为预测时间,因此,式(9)中时间t为最后一次地震到2019年12月31日的时间与预测时间t_p之和,引入截止时间能使要计算的地震的时间概念清楚。对各个地震带的预测统一为相同时间t_p=1年,否则若以t₀为基准,

表1 云南地震带地震发生的理论概率
Tab.1 Theoretical probability of earthquake occurrence in Yunnan seismic belt

由于各地震带有不同t₀,计算的未来地震发生的时间就不相同。

根据上述规定,从表1及图5可见,云南各个地震带的强震序列,以时间间隔逐渐增长和时间间隔无规律2种过程居多,未发现序列时间间隔逐渐减小过程,小江地震带累积频度随时间呈非线性增长,但增长幅度不大(图5b),在这种情况下非稳态概率大于稳态概率; 澜沧—耿马地震带累积频度随时间呈线性增长(图5h),非稳态概率与稳态概率大致相同; 大部分地震带累积频度随时间呈非线性减小,非稳态概率小于稳态概率。从图5还可以看到,曲线向下弯曲越多非稳态概率和稳态概率相差越大,如宁蒗—盐源、腾冲—龙陵、思茅—普洱地震带。

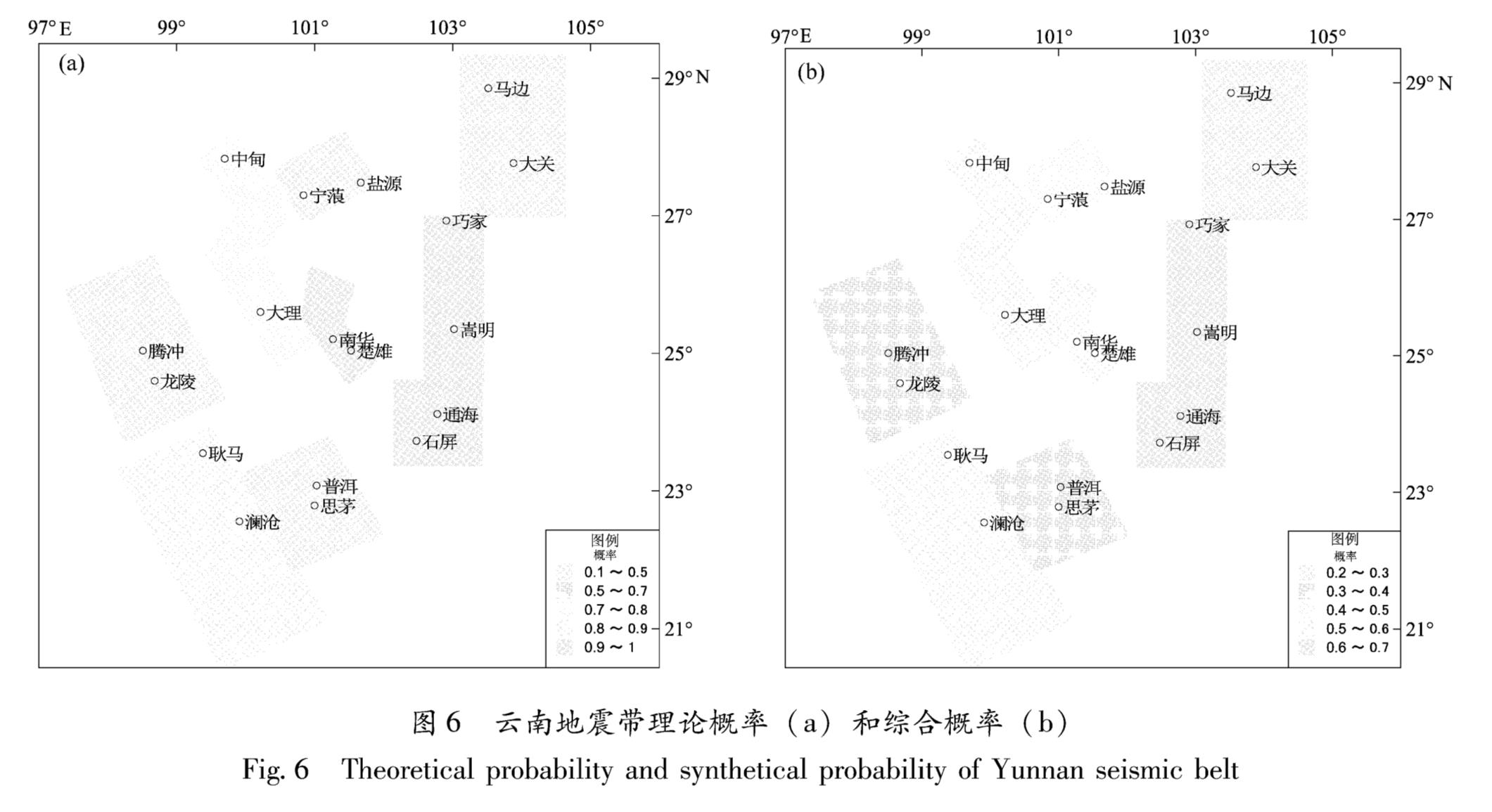
图6a给出云南各地震带非稳态泊松分布的概率模型预测未来t_p=1年地震发生理论概率,从图中可以看到,理论概率最高的地震带为通海—石屏地震带、小江地震带和楚雄—南华地震带,中甸—大理地震带和澜沧—耿马地震带次之,其它地震带理论概率较小,这个结果与本文根据计算下次地震发震时间做出的初步危险性判定结果一致。

图6 云南地震带理论概率(a)和综合概率(b)
Fig.6 Theoretical probability and synthetical probability of Yunnan seismic belt

表1仅给出根据非稳态泊松分布的概率模型计算的理论概率值,一些因素对预测结果存在影响,需要在理论计算的基础上进行综合考虑。从表1可以看出,一些地震带地震的预测时间比目前时间早,即按理论计算地震应该已经发生,但实际上还未发生,表2给出目前至预测地震的时间间隔(Y₃)参数,当Y₃为正数时表示预测时间提前,这种情况涉及到小江地震带、通海—石屏地震带、中甸—大理地震带、楚雄—南华地震带和澜沧—耿马地震带,其中小江地震带、通海—石屏地震带和中甸—大理地震带预测提前的时间较多。整体来看,以下一些因素可能对地震预测造成影响:

(1)时间间隔。这是单纯利用平静时间来预测地震的危险程度,平静时间越长发震的可能性就越大,表2给出目前至预测地震的时间间隔(Y₃)参数,Y₃越大平静时间越长,在综合考虑预测结果时,对时间间隔这一因素,认为Y₃越大,对综合概率P的贡献越大。

(2)预测精度。从图5看到,实际值与理论预测值的误差越小,预测的信度越高,使用平均绝对百分比误差MAPE来衡量预测精度:

MAPE=1/n∑ⁿ_i=1〖JB<3|〗(y_i-Ay^G1_i)/(y_i)〖JB>3|〗(10)

式中:y_i,Ay^G1_i分别为预测对象的实际值和预测值。表2中给出了各地震带的MAPE值(Y₂),绝大多数在15%以内,马边—大关地震带、小江地震带和思茅—普洱地震带误差偏大。因此,在综合考虑预测结果时,对预测精度这一因素,认为MAPE值越小,对综合概率P的贡献越大。

(3)最后地震的震级。某地区发生较大地震后再次发生地震的时间一般比相对较小地震后平静的时间要长,即大地震后能量释放较为彻底,需要更长的时间来进行能量积累。上文提到一些地震带理论计算的地震早应该发生,但实际却没有发生,从这些地震带的最后地震震级来看,目前至预测地震的时间间隔(Y₃)较长的地震带为小江地震带、通海—石屏地震带和中甸—大理地震带,后2个地震带最后地震震级均大于等于7级,地震后实际平静时间超出理论值可以用能量积累需要更长时间来解释。表2给出各地震带最后地震震级(Y₄),在综合考虑预测结果时,对最后地震震级这一因素,认为震级M越小,对综合概率P的贡献越大。

(4)资料长度。从图5可以看到,由于各地震带地震活动水平和历史地震记录完整性不同,资料的使用时间长度是不同的,资料的时间越长越能较全面反映该地区地震活动状态,预测信度也越高,表2给出各地震带资料长度(Y₅),在综合考虑预测结果时,对资料长度这一因素,认为资料越长,对综合概率P的贡献越大。

表2 云南地震带综合概率
Tab.2 Synthetical probability of earthquake occurrence in Yunnan seismic belt

由于目标是考虑诸多因素对理论计算概率值的影响,假设各个因素(或单项)对综合概率P的总贡献(或权重ω)为1,则理论概率(Y₁)的权重ω₁应大于Y₂～Y₅各单项权重,Y₂～Y₅各项取等权重。因此,各权重可取为:

ω_i=(ω₁,ω₂,ω₃,ω₄,ω₅)=(0.3,0.15,0.15,0.15,0.15)(11)

满足∑⁵_i=1ω_i=1。

对表2中Y₁～Y₅各列进行归一化处理(其中Y₂,Y₄先取倒数),利用权重集成法计算综合概率P(陈立德,1993):

P=∑⁵_i=1ω_iY_i=ω₁Y₁+ω₂Y₂+ω₃Y₃+ω₄Y₄+ω₅Y₅(12)

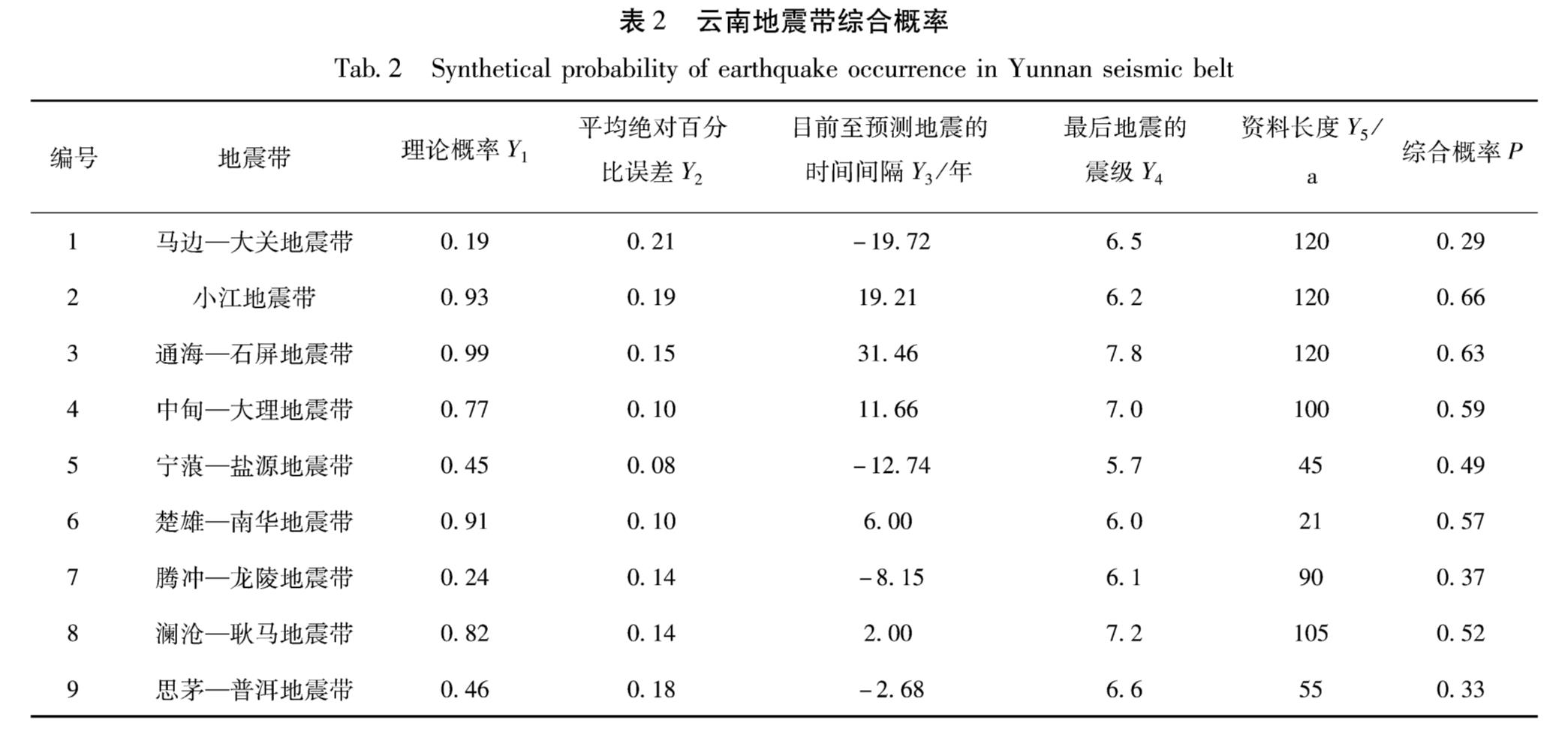
从表2的理论概率与综合概率的变化可以看到,小江地震带、通海—石屏地震带和楚雄—南华地震带理论概率较高,计算后综合概率均出现一定减小,小江地震带是由于误差(MAPE)较大,通海—石屏地震带是由于最后地震震级达7.8级,楚雄—南华地震带是由于资料时间较短。马边—大关地震带综合概率出现一定增大,是由于Y₃,Y₅贡献较多。从图6b可以看到,小江地震带和通海—石屏地震带综合概率相对较高,范围为0.60～0.69,中甸—大理地震带、楚雄—南华地震带和澜沧—耿马地震带综合概率次之,范围为0.50～0.59,其它地震带综合概率相对较小。