1.1 观测数据
相对重力测量采用周期性复测的形式进行观测,一年观测2期,测区上半年观测于每年的3—5月完成,下半年于7—9月完成。2017年以前云南省地震局主要承担滇东北、滇中、滇西南的相对重力观测任务,2018年以后,重力学科组根据属地原则进行测区调整,云南省地震局除了接手中国地震局第一监测中心在云南区域的测量任务外,还在空白区域增设测点,实现了相对重力观测对云南省行政区域的全覆盖,监测区域如图1所示。
2014年云南省地震局引进2台CG-5相对重力仪(编号分别为CG-1169,CG-1170),用于相对重力观测。洪涛等(2016)对2014年的观测数据进行研究,结果表明2台仪器的一次项系数存在变化差异。云南高山谷地纵横交错,重力测值跨度超过1 000×10-5 m/s2,微小的一次项系数偏差会对计算结果造成较大的系统误差,直接对地震趋势分析造成影响。
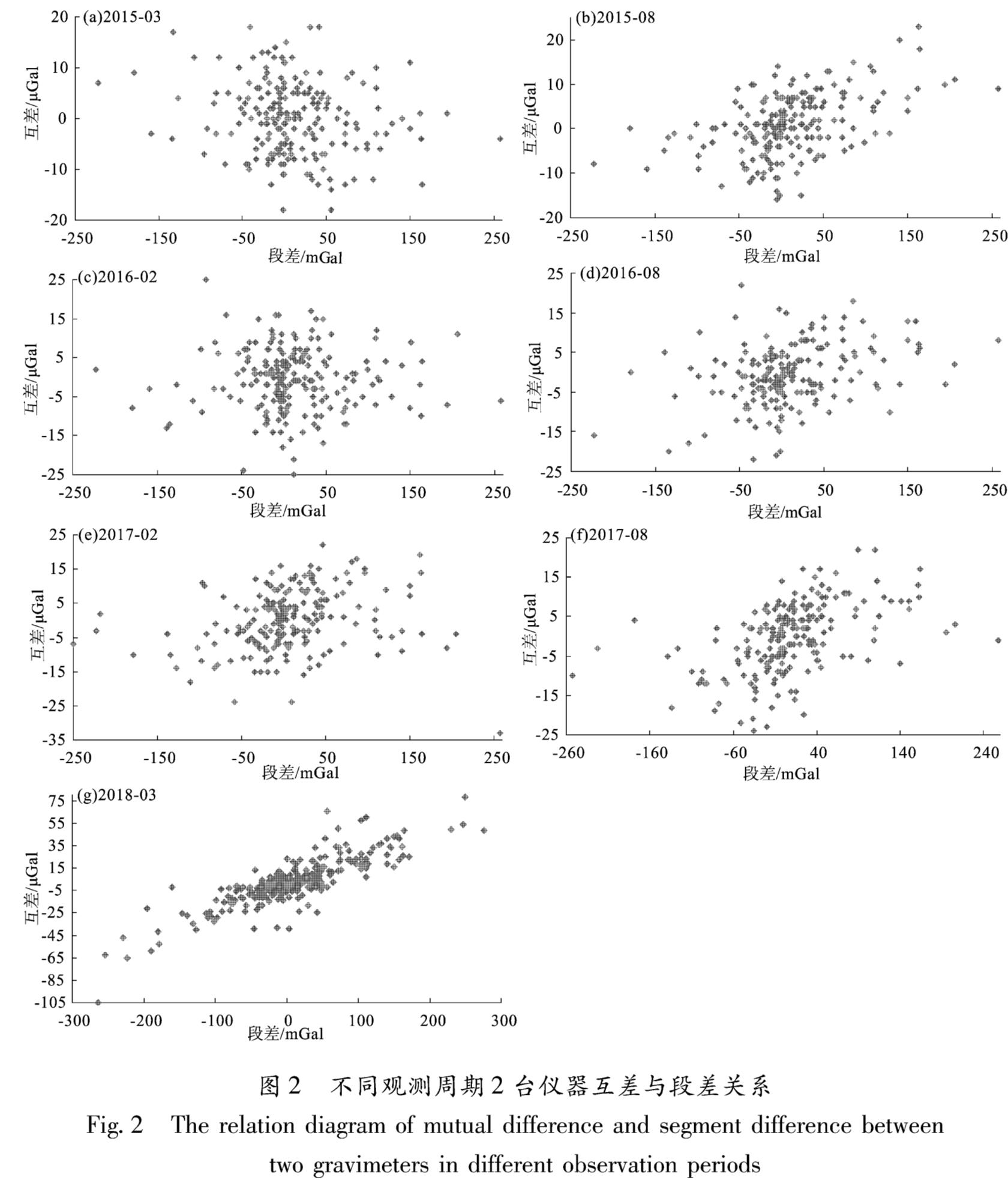
根据《国家重力控制测量规范》(GB/T 20256—2006)规定,段差是重力测量中相邻2个点间的重力差值,互差为2台仪器同时观测同一段差之差。根据《地震重力测量规范》(国家地震局,1979)规定,G型相对重力仪的一次项系数一般每隔3年须使用长基线标定一次。因此,重力学科组于2014年底组织全国地震系统内的重力仪进行长基线标定,其中云南省地震局2台仪器一次项系数标定结果分别为CG-1169:1.000 006,CG-1170:1.000 031。利用该标定结果,对2015年3月至2018年3月共7期的观测资料进行计算,统计分析2台仪器测值互差及段差的关系,结果如图2所示(图中横坐标表示2点之间的重力差值,简称为段差,纵坐标表示2台仪器同一段差的差值,简称为互差)。
从图2可以看出,在2015年3月观测时,2台仪器互差随段差的变化成离散状态,总体呈正态分布,符合偶然误差的分布规律; 2015年8月至2017年8月2台仪器互差随段差的变化趋势逐渐明晰,但是绝对差异值均在规定的限差(30×10-8 m/s2)之内,到2018年3月时2台仪器互差与段差的关系总体已经成线性关系,差异值已经突破100×10-8 m/s2,这种情况下,继续使用2014年长基线标定的一次项系数进行计算必然会导致较大误差,因此必须进行一次项系数修正。因为互差随段差变化趋势总体呈成线性关系,可以采用线性回归分析的方法进行分析,首先建立数学模型。
图1 云南省相对重力观测点分布图
Fig.1 Map showing relative gravity observation sites in Yunnan province
图2 不同观测周期2台仪器互差与段差关系
Fig.2 The relation diagram of mutual difference and segment difference between two gravimeters in different observation periods
1.2 数学模型
根据CG-5重力仪出厂参数,其非线性系数已经调整为0,观测值仅考虑其一次项标定系数即可。在不考虑偶然观测误差的情况下,某个测点上的读数值数学模型为:
F(Xi)=E(Xi+x0+δ漂+δ固+t温+p压+h高)(1)
式中:E为一次项系数; Xi为该点重力值; x0为仪器零重力值读数; δ漂为零漂改正; δ固为固体潮改正; t温为温度改正; p压为气压改正; h高为仪高改正。
CG-5为相对重力观测仪器,式(1)中x0为未知数,如果没有联测基准点,在某一个测点上的仪器读数不具备物理意义,但是对相邻2个观测点进行差值计算后消除x0,剩下的各项改正均可通过观测其他物理量或经验公式获取,最终结果即为2个测点的段差。
因此,CG-5重力仪对相邻2个测点的段差观测值数学模型可简化为:
F(Xij)=(E+ΔE)(Xi-Xj)(2)
式中:ΔE为一次项系数差异。
由于2台仪器同时同地观测,其观测结果不存在物理量差异,如果观测二者存在系统误差,可以判定为是由于一次项系数差异ΔE引起的,其数学模型可表示为:
DXij=(E1+ΔE1)(Xi-Xj)-(E2+ΔE2)(Xi-Xj)=ΔE12(Xi-Xj)(3)
其误差方程为:
vij=ΔE12(Xi-Xj^-)-DXij(4)
在实际观测中,互差DXij可以作为观测值直接得出,其量级(×10-8 m/s2)远远小于段差(Xi-Xj^-)(×10-5 m/s2),因此可以采用2台仪器段差的平均值作为(Xi-Xj^-)。
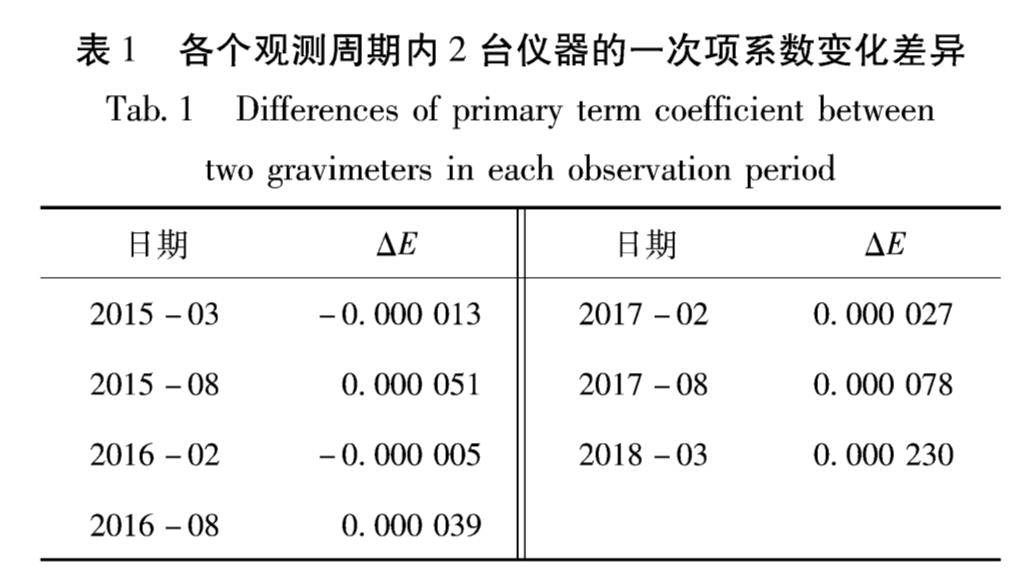
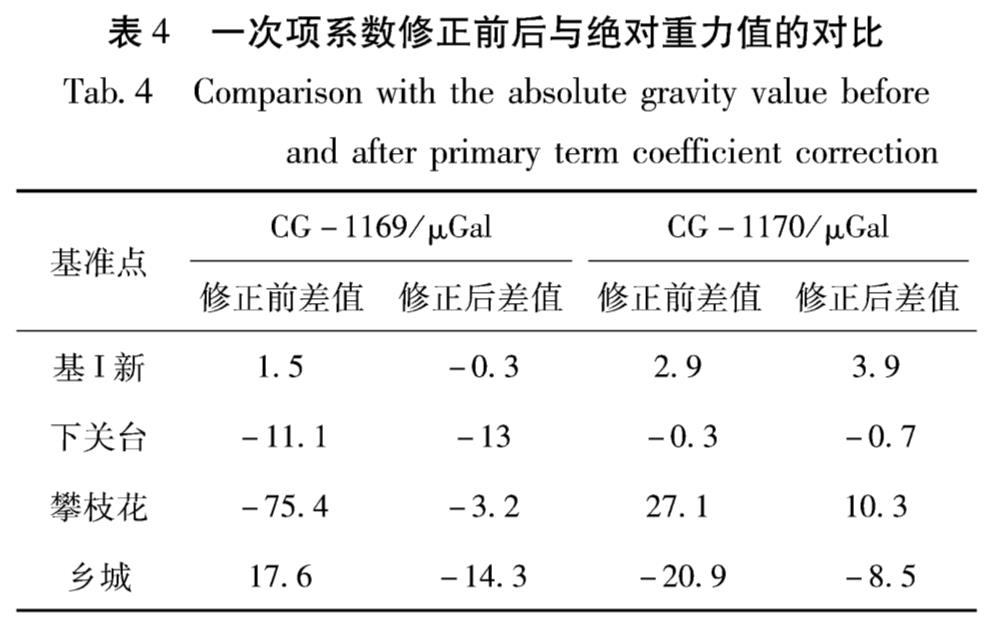
将7期观测数据分别带入式(4),利用经典平差方法结算,计算出每期2台仪器一次项系数变化的差异ΔE见表1。
从表1可以看出,2台仪器的一次项系数变化差异在各期均不一致,随着时间推移总体呈增大趋势,在2018年3月观测时,已经达到万分之二以上,对重力值跨度超过1 000 000×10-8 m/s2的云南区域影响明显。
表1 各个观测周期内2台仪器的一次项系数变化差异
Tab.1 Differences of primary term coefficient between two gravimeters in each observation period
1.3 在同一观测周期内一次项系数随时间变化分析
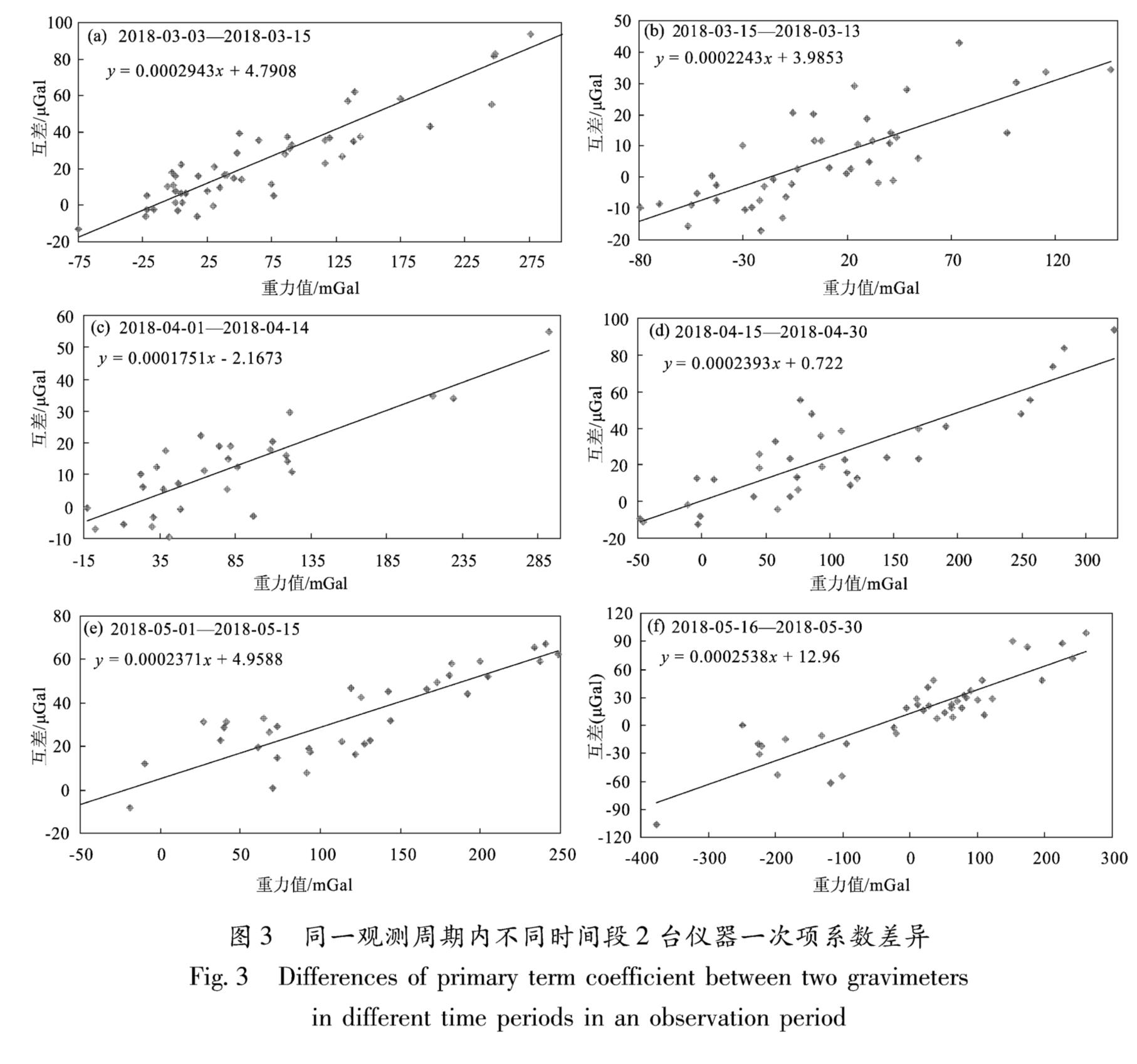
每一期观测时,重力仪一次项系数与上期均有变化,且2台仪器变化是存在差异的。完成一个观测周期大概需要60~100 d,为了分析此期间内2台仪器的一次项系数的变化差异特性,本文以差异较为明显的2018-03期为例,在一个观测周期内,以15 d为间隔,对2台仪器的一次项系数差异进行计算,结果如图3所示。
图3 同一观测周期内不同时间段2台仪器一次项系数差异
Fig.3 Differences of primary term coefficient between two gravimeters in different time periods in an observation period
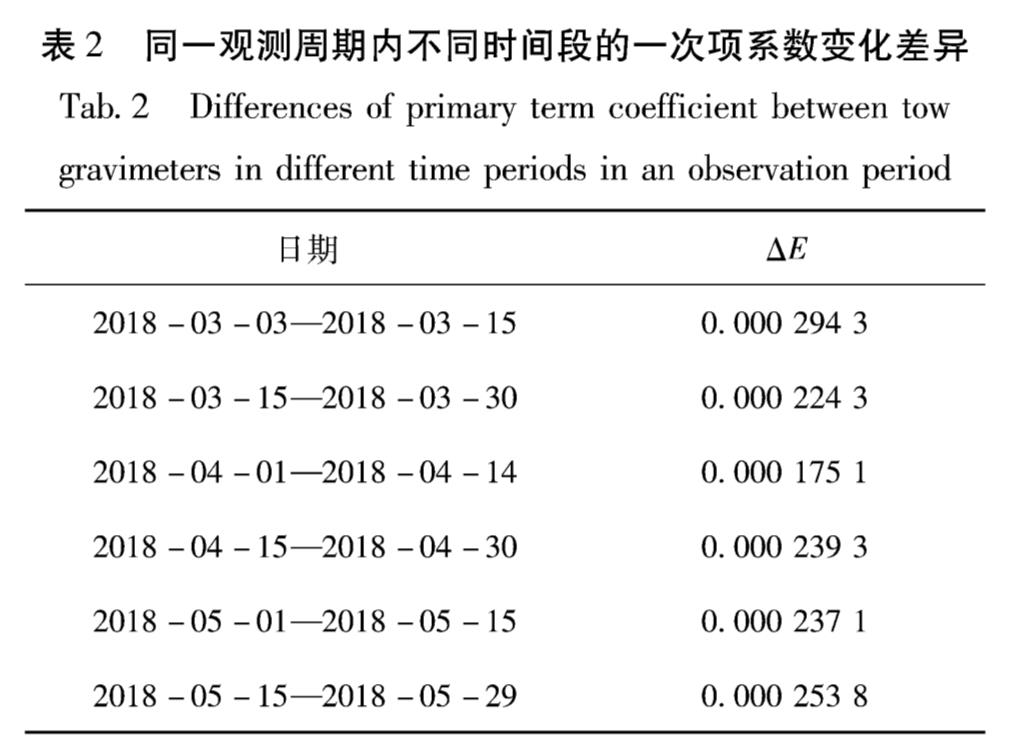
从图3可以看出,由于总样本被拆分成多个小样本,数据量减少,观测误差对回归分析结果影响增大,但是在一个观测周期的不同时间段,2台仪器一次项系数差异总体趋势是一致的,不同时间段变化并不大。通过线性回归分析,不同时间段2台仪器一次项系数差异如表2所示。
表2 同一观测周期内不同时间段的一次项系数变化差异
Tab.2 Differences of primary term coefficient between tow gravimeters in different time periods in an observation period
从表2可以看出,在一个观测周期内的不同时间段里,2台仪器的一次项系数差异变化不大,与全样本量总体计算的一次项系数差异的偏差均在万分之一以内。因此,可以认为在一个观测周期内的不同时间段可采用同一个一次项系数。
1.4 在一次观测周期内一次项系数随测值段的变化分析
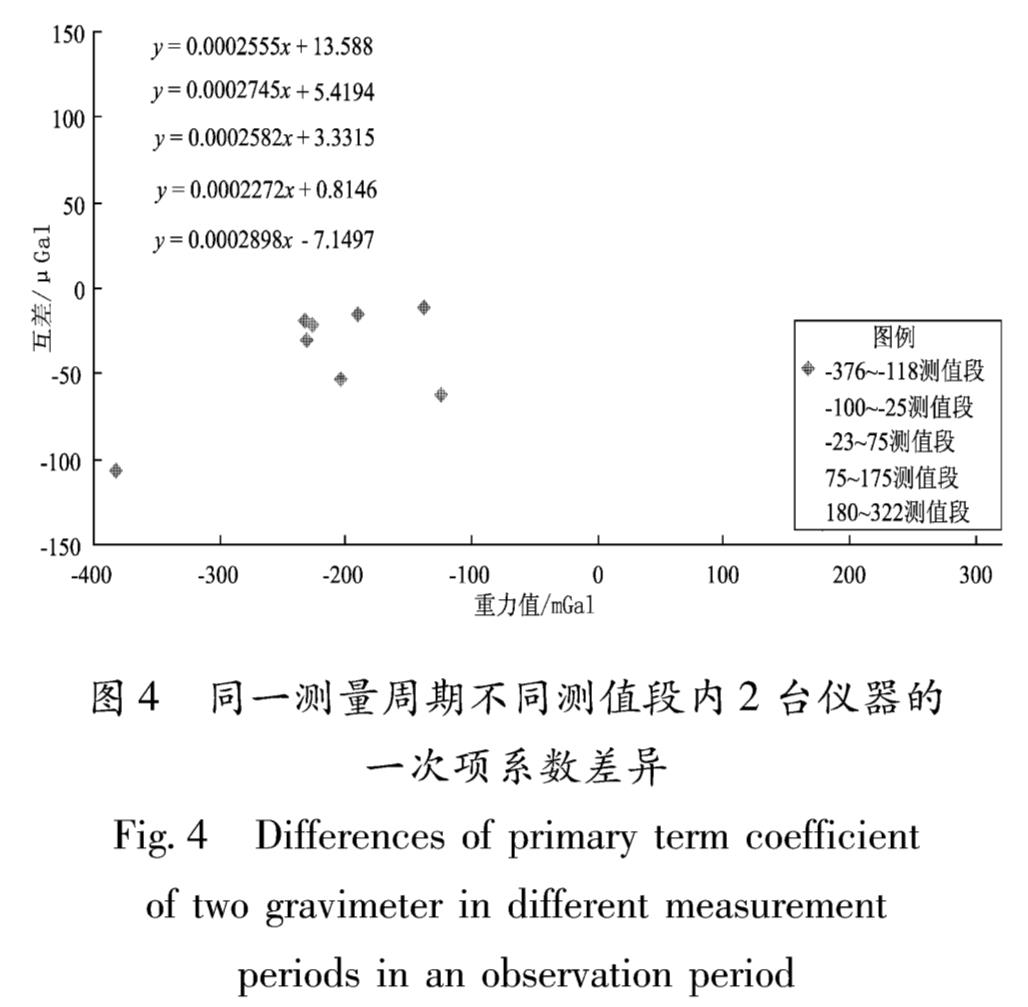
测值段的变化包含两部分:一是由于零漂造成的仪器自身测值段变化,二是由于空间重力变化引起的测值段变化。根据观测经验及已有文献分析可知,CG-5仪器漂移较大,日变化率能达到1 000×10-8 m/s2(汪健等,2016; 邢乐林等,2010),造成观测值段一直在增大。直观上看,一次项系数与测值段似乎存在相关性,为了研究云南测区内2台仪器一次项系数变化与观测值段的关系,以2018-03期观测结果为例,在合理分配测值段及样本量的情况下,将观测结果大致按150 mGal的间隔拆分,分别计算每个测值段的2台仪器一次项系数差异,结果如图4所示。
从图4可以看出,虽然样本量减少,观测误差影响增大,但是不同观测值段内2台仪器的一次项系数差异总体趋势一致,与全样本量计算结果偏差较小,因此可以认为,在一个观测周期内的不同观测值段,均可采用统一的一次项系数。
图4 同一测量周期不同测值段内2台仪器的一次项系数差异
Fig.4 Differences of primary term coefficient of two gravimeter in different measurement periods in an observation period
1.5 各观测周期一次项系数计算
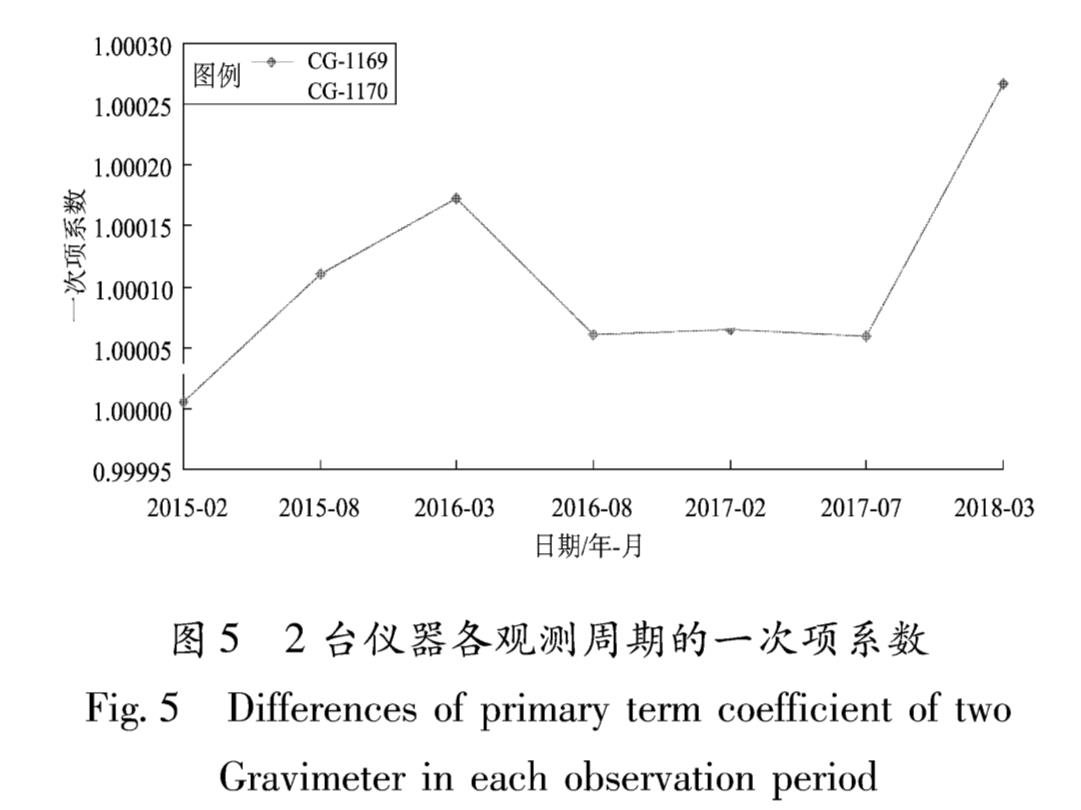
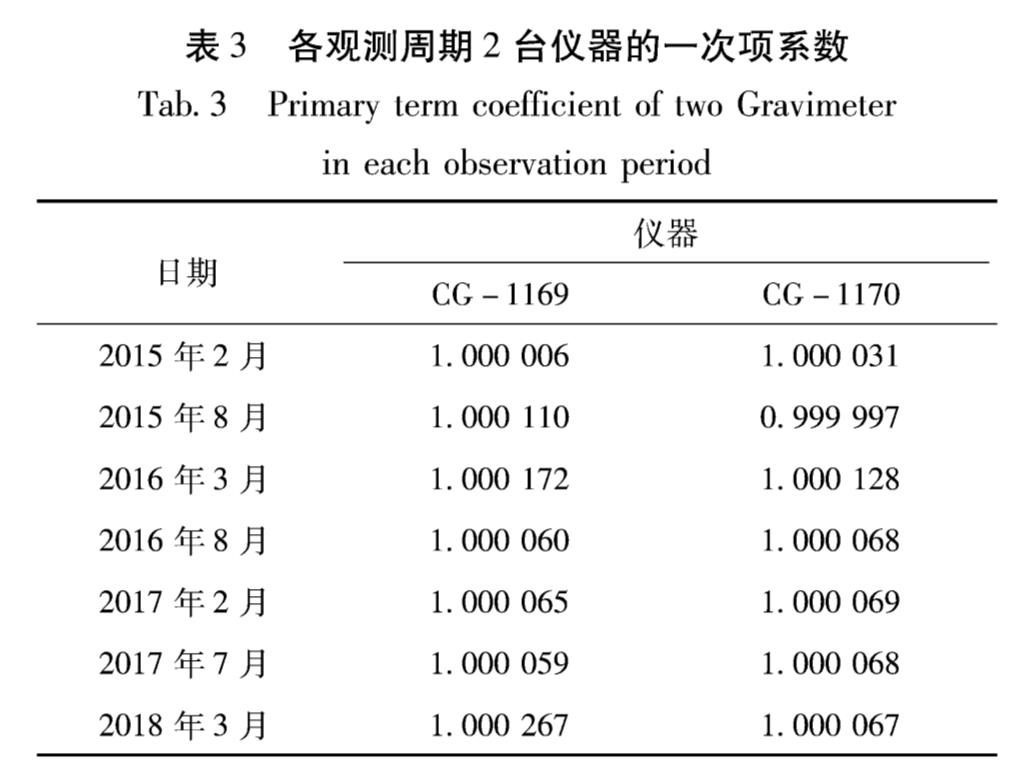
根据上述研究可知,1台仪器在一个观测周期内可以采用统一的一次项系数。考虑到云南测区地面起伏较大,海拔跨度超过3 000 m,高山与低谷交错纵横,测点在不同海拔均有分布,鉴于在短期内真实重力变化与段差呈线性关系的可能性不大,因此可认为相邻观测周期间段差变化与段差呈线性关系主要是因为2期一次项系数的偏差。于是可以将2期段差变化作为DXij,2期段差平均值作为(Xi-Xj^-),代入式(4)中,利用2014年12月全国标定的结果作为2015年3月观测资料的一次项系数,逐期计算一次项系数差异,并计算每期一次项系数的最或然值,结果见图5及表3。
图5 2台仪器各观测周期的一次项系数
Fig.5 Differences of primary term coefficient of two Gravimeter in each observation period
表3 各观测周期2台仪器的一次项系数
Tab.3 Primary term coefficient of two Gravimeter in each observation period
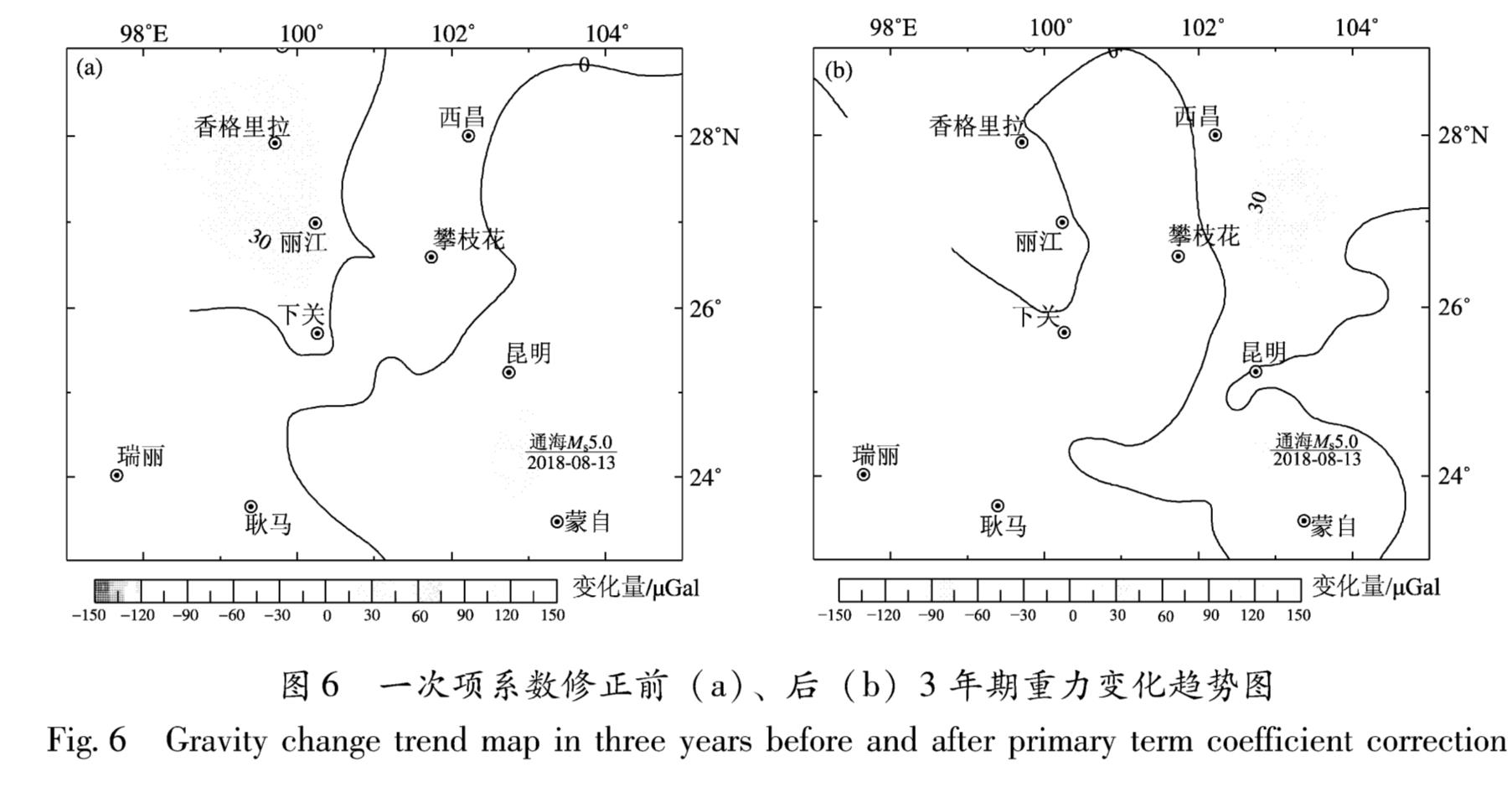
通过图5及表3可以看出,编号CG-1169仪器一次项系数从2015年3月至2016年8月有所变化,2016年8月至2017年7月相对稳定,2018年3月出现突变,3年内随时间变化达到0.000 261; 编号CG-1170仪器2015年3月至2016年8月有所变化,其后一直比较稳定,3年内一次项系数累计变化为0.000 036。2台仪器3年内累计变化差异为0.000 224,与独立分析2018-03期得出的差异基本一致,可以认为表3结果为仪器观测时的实际一次项系数。